Abstract
We describe Peirce’s 1903 system of modal gamma graphs, its transformation rules of inference, and the interpretation of the broken-cut modal operator. We show that Peirce proposed the normality rule in his gamma system. We then show how various normal modal logics arise from Peirce’s assumptions concerning the broken-cut notation. By developing an algebraic semantics we establish the completeness of fifteen modal logics of gamma graphs. We show that, besides logical necessity and possibility, Peirce proposed an epistemic interpretation of the broken-cut modality, and that he was led to analyze constructions of knowledge in the style of epistemic logic.




Similar content being viewed by others
Notes
Namely (1) to answer the problem of the soundness of reasoning, (2) to develop new methods for logical analysis, (3) to address the question of the nature of mathematical reasoning, and (4) to present his philosophical account of the relation of qualities and laws to forms of thought.
The draft page presents a list of “special spot-graphs”, among which we find graphs for necessity, possibility, and possibility of necessity. These three were omitted from the printed version because of the cost and the typographical complications that they presented to the printer, and were replaced by Convention No. VIII.: “1. A cut with many little interruptions aggregating about half its length shall cause its enclosure to be a graph, expressing that the entire graph on its area is logically contingent (non-necessary)” [R 479, p. 19; cf. (Roberts 1973, p. 82)].
Soon after the lectures, Peirce communicates with with the Putnam & Sons to get his Lowell Lectures published. His correspondence with James McKeen Cattell and G. Putnam (R L 78) reveals that the publication of the lectures fell through merely for accidental and commercial reasons. The full corpus of his lecture notes for the Lowell Lectures consisted of altogether some 1300 manuscript pages and would have made a major contribution to the study of logic of the time—and would be a major contribution to the study of logic of our time, too, one might add.
We emphasize that the continuous cut means negation derivatively, namely that it is a result of having the sign of illation (“the scroll”) first, from which a cut that means negation results by atrophying the inner loop invisibly small (R S-30 Peirce 1896–1906; cf. Bellucci and Pietarinen 2016). We also note that negation is only one meaning of the continuous cut among many, as it also serves (1) the role of what parentheses do in the linear notation, (2) the grouping together of propositions, as well as (3) being an indicator of the context for subgraphs.
Peirce admits that more than two kinds of cuts may be needed in practice, but he notes to have found real use for only two of them: the continuous and the broken cut. At first (R S-28, September 1903 Peirce 1896–1906), he proposes that it is the “mode of dotting the line” that identifies what alternative universes are meant (this is his Convention 9). Later he rather takes it that if new and different modes of modalities are needed, those are better represented not by changes in the kind of line drawn to enclose other graphs, which really is nothing but the boundary between the areas inside and outside it, but by changes in the quality of those areas, that is, by tinctured graphs (R 295/292b, 1906 Peirce 1906c).
The term “nest” was first presented in July 10, 1903, in the Logic Notebook (R 339, Peirce 1865–1909).
Peirce is not fully consistent as to this aspect of the system. He wrote in R 467 (Peirce 1903b): “Rules of the Broken Cut: Rule I. In a broken cut already on the sheet of assertion any graph may be inserted”. In the drafts of the Syllabus he states that the rule of erasure and insertion “applies to the broken cut”, which is correct. In the last draft of the Syllabus, he states that “The Rule of Erasure and Insertion applies to the broken cut in this form: Evenly enclosed, a full cut can be transformed into a broken cut; while oddly enclosed a broken cut can be transformed into a full one. It makes no difference whether the enclosure here spoken of is by a full or a broken cut. In regard to Graphs the Rule of Erasure and Insertion applies to enclosures by broken cuts precisely as to those by full cuts”. This is also correct.
In the tinctured graphs, which we do not propose to study here, there can be differently tinctured provinces in the same graph and which correspond to multi-modal logics, but this does not change the rule (K) in any way.
Since all derivations begin with the sheet of assertion, which is \(\top \), there is no need to separately state that G in the premiss needs to be a theorem of the system.
It is unclear whether Peirce used in R 478(s) Peirce (1903e) the sign of consequence (
 ) or the sign of equality (\(=\)) between
) or the sign of equality (\(=\)) between 
and

; possibly he first wrote
 , but then crossed it over with \(=\). The latter direction would mean also density, that is, a deletion of a doubled necessity around a graph, producing yet another modal system.
, but then crossed it over with \(=\). The latter direction would mean also density, that is, a deletion of a doubled necessity around a graph, producing yet another modal system.A further point of interest concerning the behaviour of the double broken cut is that Peirce took the outer broken cuts to be relative not to a state of information “but to a state of reflection”, namely to the possibility that the truth of the graph is necessary, and that it is because of the ignorance, or that one has “not sufficiently reflected upon the subject” (R 467 Peirce 1903b) that doubt remains whether the truth of the graph obtains or not. An interested reader may compare Peirce’s argument to Anselm’s ontological proof that turn on interpretations of Brouwer’s Axiom (Serene 1981), or to the logic of ‘being informed’ (Floridi 2006), for example.
This algebraic semantics and its application to the Gamma graphs is not intended to capture all aspects of what a comprehensible semantic theory for EGs ought to accomplish, such as Peirce’s own game-theoretic interpretation of graphs in terms of the actions of the Graphist and the Interpreter (for such an interpretation, see e.g. Pietarinen 2006b). The extension of game-theoretic semantics to modalities is straightforward. Yet we believe that algebraic semantics is worth developing as well and that its application to the the theory of graphs justified also from the point of view of Peirce’s own logical theorizing, because (1) it continues the algebraic tradition of logic that largely originated with Peirce’s logical researches, and because (2) these graphical systems admit of a reinterpretation in terms of algebraic rules. The algebraic viewpoint thus answers the remark we find in Peirce’s reply to Ladd–Franklin’s question of what bearing logical graphs have on the received basic logic: “Not much”, he answered, “except in one highly important particular, that they supply an entirely new system of fundamental assumptions to logical algebra” (R L 237, 1900 Peirce 1900).
Another, possibly equivalent term for a perfect system of rules was that they consist of an “archegetic rules of transformation”. He explains this as the property of “the rules of any code which is such that none of its rules follows as a consequence from the rest, while all other permissibilities are consequences of its rules” (R 478 Peirce 1903e). This characterises another property, the independence of the rules of transformation.
We should also notice the novelty that broken cuts have, unlike continuous cuts, special hooks onto which we can connect such marks that refer to the states of things, or possible worlds. Peirce explains this procedure as follows:
We should fall into inextricable confusion in dealing with the broken cut if we did not attach to it a sign to distinguish the particular state of information to which it refers. And a similar sign has then to be attached to the simple g, which refers to the state of information at the time of learning that graph to be true. (R 467 Peirce 1903b)
Modalities are thus connected to “states of information” to which they refer. The passage above is then followed by the presentation of the necessitation rule, namely that from a graph g that has been marked by the attachment to the hook of the broken cut (namely that one has already learned or proven the graph to be true), we can infer the necessity of that graph g. The idea of hooks comes from the Beta graphs, in which they surround the periphery of “spots” (the predicate and relation terms) and into which the quantifiers, as lines of identity, are attached.
Cf. R 467 Peirce (1903b): “It becomes evident, in this way, that a modal proposition is a simple assertion not about the universe of things but about the universe of facts that one is in a state of information sufficient to know. The graph

without any selective, merely asserts that there is a possible state of information in which the knower is not in a condition to know that the graph g is true, while

asserts that there is no such possible state of information.”
We use subscript indices here instead of connecting lines that Peirce used in the original caption of the graph in Fig. 4c. Peirce also wrote “not quite sure” below this graph.
References
Bellucci, F., & Pietarinen, A.-V. (2016). Existential graphs as an instrument for logical analysis. Alpha, Review of Symbolic Logic, 9, 209–237.
Caterina, G., & Gangle, R. (2010). Consequences of a diagrammatic representation of Paul Cohen’s forcing technique based on C. S. Peirce’s existential graphs. In L. Magnani (Ed.), Model-based reasoning in science and technology (pp. 429–443). Berlin: Springer.
Floridi, L. (2006). The logic of being informed. Logique and Analyse, 196, 1–28.
Hintikka, J. (1962). Knowledge and belief: An introduction to the logic of the two notions. Cornell: Cornell University Press.
Ma, M., & Pietarinen, A.-V. (2017a). Peirce’s sequent proofs of distributivity. In Ghosh, S., & Prasad, S. (Eds.), Logic and its applications: Proceedings of the 7th Indian logic conference, lecture notes in computer science (Vol. 10119, pp. 168–183).
Ma, M., & Pietarinen, A.-V. (2017b). Graphical sequent calculi for modal logics. In The 9th workshop on methods for modalities, electronic proceedings in theoretical computer science (pp. 91–103).
Øhrstrøm, P. (1995). Graphs for time and modality. In P. Øhrstrøm & R. Hasle (Eds.), Temporal logic: From ancient ideas to artificial intelligence (pp. 320–343). Dordrecht: Kluwer Academics.
Peirce, C. S. (1865–1909). The logic notebook (R 339).
Peirce, C. S. (1896–1906). [Notes on logical graphs]. Supplements (S-26, S-28, S-30, S-31).
Peirce, C. S. (1900). Letter to Christine Ladd-Franklin, November 9 (R L 237).
Peirce, C. S. (1903a). Lowell lectures. Lecture III (R 462, S-31).
Peirce, C. S. (1903b). Lowell lectures. Lecture IV. Existential graphs, gamma part (R 467, R 470, S-31).
Peirce, C. S. (1903c). Lowell lectures. Lecture V (R 468–470).
Peirce, C. S. (1903d). Lowell lectures. Notes on graphs. Notebook (R 496).
Peirce, C. S. (1903e). A syllabus of certain topics of logic. Boston: Alfred Mudge & Son. (R 478, 478(\(s\))).
Peirce, C. S. (1904). Reason’s conscience. A practical treatise on the theory of discovery; considered as semeiotic (R 693a, R S-26).
Peirce, C. S. (1906–7). (PAP) (R 293).
Peirce, C. S. (1906a). On existential graphs as an instrument of logical research (R 470, 498–499, S-36).
Peirce, C. S. (1906b). Prolegomena to an apology for pragmaticism. Monist, 16, 492–546.
Peirce, C. S. (1906c). Prolegomena to an apology for pragmaticism. Draft versions (R 295/292b).
Peirce, C. S. (1908). The bed-rock beneath pragmaticism (R 300).
Peirce, C. S. (1910). Diversions of definitions (essays definitions) (R 650).
Peirce, C. S. (1911a). Assurance through reasoning (R 669).
Peirce, C. S. (1911b). Letter to Risteen: A diagrammatic syntax. December 6 (R L 376).
Peirce, C. S. (1931–1966). The collected papers of Charles S. Peirce (C. Hartshorne, P. Weiss, & A. W. Burks, Eds.), (Vol. 8). Cambridge: Harvard University Press. (Cited as CP followed by volume and paragraph number).
Peirce, C. S. (1966). Manuscripts in the Houghton Library of Harvard University, as identified by Richard Robin, Annotated Catalogue of the Papers of Charles S. Peirce, Amherst: University of Massachusetts Press, 1967, and in The Peirce Papers: A supplementary catalogue, Transactions of the C.S. Peirce Society 7 (1971): 37–57. (Cited as R followed by manuscript number and, when available, page number).
Peirce, C. S. (1976). The new elements of mathematics by Charles S. Peirce. (C. Eisele, Ed), (Vol. 4). The Hague: Mouton. (Cited as NEM followed by volume and page number).
Peirce, C. S. (1982-). Writings of Charles S. Peirce: A chronological edition. (E. C. Moore, C. J. W. Kloesel, et al. Eds.), (Vol. 7). Bloomington: Indiana University Press. (Cited as W followed by volume and page number).
Pietarinen, A.-V. (2001). Intentional identity revisited. Nordic Journal of Philosophical Logic, 6, 144–188.
Pietarinen, A.-V. (2006b). Signs of logic: Peircean themes on the philosophy of language, games, and communication. Dordrecht: Springer.
Pietarinen, A.-V. (2008a). The proof of pragmatism: Comments on Christopher Hookway. Cognitio, 9(1), 85–92.
Pietarinen, A.-V. (2008b). Diagrammatic logic of existential graphs: A case study of commands. In G. Stapleton, J. Howse, & J. Lee (Eds.), Diagrammatic representation and inference, lecture notes in computer science (Vol. 5223, pp. 404–407). Heidelberg: Springer.
Pietarinen, A.-V. (2011a). Existential graphs: What the diagrammatic logic of cognition might look like. History and Philosophy of Logic, 32(3), 265–281.
Pietarinen, A.-V. (2011b). Moving pictures of thought II: Graphs, games, and pragmaticism’s proof. Semiotica, 186, 315–331.
Pietarinen, A.-V. (2015a). Exploring the beta quadrant. Synthese, 192, 941–970.
Pietarinen, A.-V. (2015b). Two papers on existential graphs by Charles S. Peirce: 1. Recent developments of existential graphs and their consequences for logic (MS 498, 499, 490, S-36, 1906), 2. Assurance through reasoning (MS 669, 670, 1911). Synthese, 92, 881–922.
Pietarinen, A.-V., & Snellman, L. (2006a). On Peirce’s late proof of pragmaticism. In T. Aho & A.-V. Pietarinen (Eds.), Truth and games (Vol. 78, pp. 275–288). Helsinki: Acta Philosophica Fennica.
Prior, A. N. (1957). Time and modality. Oxford: Oxford University Press.
Ramharter, E., & Gottschall, C. (2011). Peirce’s search for a graphical modal logic (propositional part). History and Philosophy of Logic, 32, 153–176.
Roberts, D. D. (1973). The existential graphs of Charles S. Peirce. The Hague: Mouton.
Serene, E. F. (1981). Anselm’s modal conceptions. In S. Knuuttila (Ed.), Reinforcing the great chain of being: Studies of the history of modal theories (pp. 117–163). Dordrecht: Springer.
Zeman, J. (1964). The graphical logic of Charles S. Peirce. Ph.D. dissertation. University of Chicago.
Zeman, J. (1967). A system of implicit quantification. Journal of Symbolic Logic, 32, 480–504.
Acknowledgements
We thank the four anonymous reviewers of the present journal for comments. Earlier versions of the paper were presented by the second author at the Workshop on Existential Graphs held in Helsinki in August 2016, at the Charles S. Peirce International Centennial Congress held at the University of Massachusetts Lowell in July 2014, and at the Modalities and Modal Logic Conference held at the University of Copenhagen in May 2012. This paper is dedicated to Jay J. Zeman, who passed away just at the time of completion of the present paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
The work of the first author is supported by Chinese National Foundation of Social Sciences and Humanities (Grant No. 16CZX049). The work of the second author is supported by the Academy of Finland (Project 1270335, Diagrammatic Mind (DiaMind): Logical and Cognitive Aspects of Iconicity) and the Estonian Research Council (project PUT 1305, Abduction in the Age of Fundamental Uncertainty), Principle Investigator A.-V. Pietarinen.
Rights and permissions
About this article
Cite this article
Ma, M., Pietarinen, AV. Gamma graph calculi for modal logics. Synthese 195, 3621–3650 (2018). https://doi.org/10.1007/s11229-017-1390-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-017-1390-3



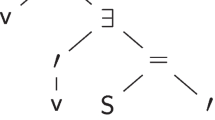

 ) or the sign of equality (
) or the sign of equality (

 , but then crossed it over with
, but then crossed it over with 
