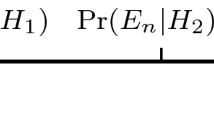Reflecting on finite additivity

Abstract

An infinite lottery experiment seems to indicate that Bayesian conditionalization may be inconsistent when the prior credence function is finitely additive because, in that experiment, it conflicts with the principle of reflection. I will show that any other form of updating credences would produce the same conflict, and, furthermore, that the conflict is not between conditionalization and reflection but, instead, between finite additivity and reflection. A correct treatment of the infinite lottery experiment requires a careful treatment of finite additivity. I will show that the results of the experiment, paradoxical though they may be, are not inconsistent, but that they conflict with one particular version of reflection (special reflection). I will reject that version and I will propose a slight modification of a different version of reflection (general reflection) such that the modified version does maintain the mutual consistency of finite additivity, reflection and conditionalization. As a result, I will strengthen the case for finite additivity by showing that Bayesian conditionalization is fully consistent with it.

Appendix

Define $\hbox {p}_\mathrm{m}\hbox {(A)} = \hbox {p}_\mathrm{m}\hbox {(B)} = 0.5, \hbox {p}_\mathrm{m}(\hbox {n}{\vert }\hbox {A}) = \hbox {p}_\mathrm{m}(\hbox {n}{\vert }\hbox {B}) = 0$ for $\hbox {n}>\hbox {m}$, while, for $\hbox {n}\le \hbox {m} , \hbox {p}_\mathrm{m}(\hbox {n}{\vert }\hbox {A}) = (\hbox {n}^{-1} + \hbox {n}^{-2}) / \hbox {C}_\mathrm{m}$ and $\hbox {p}_\mathrm{m}(\hbox {n}\vert \hbox {B}) = (\hbox {n}^{-1} - \hbox {n}^{-2}) / \hbox {D}_\mathrm{m}$. $\hbox {C}_\mathrm{m}$ and $\hbox {D}_\mathrm{m}$ are normalization constants equal to ln(m) $+$ terms of order 1. We are interested in the limit of m going to infinity.

First, we find that lim $\hbox {p}_\mathrm{m}(\hbox {A}{\vert }\hbox {n}) = (1 + \hbox {n}^{-1})/2 > 0.5$. Second, let ${\varvec{{{\mathcal {E}}}}}$ be some subset of ${\varvec{{\mathcal {N}}}}$. In that case, $\hbox {p}_\mathrm{m}(\hbox {A}{\vert }{\varvec{{{\mathcal {E}}}}}) = \hbox {p}_\mathrm{m}({\varvec{{{\mathcal {E}}}}}{\vert }\hbox {A}) / (\hbox {p}_\mathrm{m}({\varvec{{{\mathcal {E}}}}}{\vert }\hbox {A}) + \hbox {p}_\mathrm{m}({\varvec{{{\mathcal {E}}}}}{\vert }\hbox {B})) = 1 / (1 + \hbox {p}_\mathrm{m}({\varvec{{{\mathcal {E}}}}}{\vert }\hbox {B})/\hbox {p}_\mathrm{m}({\varvec{{{\mathcal {E}}}}}{\vert }\hbox {A}))$. The limit of $\hbox {C}_\mathrm{m} / \hbox {D}_\mathrm{m}$ equals 1, so the limit of $\hbox {p}_\mathrm{m}({\varvec{{{\mathcal {E}}}}}{\vert }\hbox {B})/\hbox {p}_\mathrm{m}({\varvec{{{\mathcal {E}}}}}{\vert }\hbox {A})$ equals

$$\begin{aligned} \lim \frac{C_m }{D_m }\frac{\sum {j^{-1}-j^{-2}} }{\sum {j^{-1}+j^{-2}} }=1-2\;\;\;\lim \frac{\sum {j^{-2}} }{\sum {j^{-1}-j^{-2}} }, \end{aligned}$$

in which the sums are taken over all j not exceeding m and in ${\varvec{{{\mathcal {E}}}}}$. This limit is less than or equal to 1 and, consequently, $\hbox {p}_\mathrm{m}(\hbox {A}{\vert }{\varvec{{{\mathcal {E}}}}}) \ge 0.5$. Equality obtains if the complement of ${\varvec{{{\mathcal {E}}}}}$ with respect to ${\varvec{{\mathcal {N}}}}$ is finite.