A retrial system with two input streams and two orbit queues

Abstract

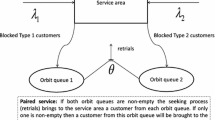
Two independent Poisson streams of jobs flow into a single-server service system having a limited common buffer that can hold at most one job. If a type-$i$ job ($i=1,2$) finds the server busy, it is blocked and routed to a separate type-$i$ retrial (orbit) queue that attempts to re-dispatch its jobs at its specific Poisson rate. This creates a system with three dependent queues. Such a queueing system serves as a model for two competing job streams in a carrier sensing multiple access system. We study the queueing system using multi-dimensional probability generating functions, and derive its necessary and sufficient stability conditions while solving a Riemann–Hilbert boundary value problem. Various performance measures are calculated and numerical results are presented. In particular, numerical results demonstrate that the proposed multiple access system with two types of jobs and constant retrial rates provides incentives for the users to respect their contracts.

Appendix

Lemma 1

Conditions (34) imply that either $\alpha \lambda _1<\mu \mu _1$ or $\alpha \lambda _2<\mu \mu _2$.

Proof

Assume that $\alpha \lambda _1\ge \mu \mu _1$ and $\alpha \lambda _2 \ge \mu \mu _2$

Multiplying the first inequality in (34) by $\mu \mu _1$ and using the definition of $\lambda$ and $\alpha$ gives

$$\begin{aligned} (\lambda _1+\lambda _2)(\lambda _1+\mu _1)< \mu \mu _1\le \alpha \lambda _1=(\lambda _1+\lambda _2+\mu _1+\mu _2)\lambda _1 \end{aligned}$$

which is true if and only if (a) $\lambda _2\mu _1<\lambda _1 \mu _2$.

Multiplying now the second inequality in (34) by $\mu \mu _2$ gives

$$\begin{aligned} (\lambda _1+\lambda _2)(\lambda _2+\mu _2)< \mu \mu _2\le \alpha \lambda _2=(\lambda _1+\lambda _2+\mu _1+\mu _2)\lambda _2 \end{aligned}$$

which is true if and only if (b) $\lambda _1\mu _2<\lambda _2 \mu _1$.

Since inequalities (a) and (b) cannot be true simultaneously we conclude that either $\alpha \lambda _1<\mu \mu _1$ or $\alpha \lambda _2<\mu \mu _2$, which concludes the proof. $\square$

Lemma 2

Under conditions (34), (i) $A(k(y),y)\not =0$ and (ii) $B(k(y),y)\not =0$ for

$y \in [y_1,y_2]$.

Equivalently, (iii) $A(x,h(x))\not =0$ and (iv) $B(x,h(x))\not =0$ for $x\in C_{\sqrt{\hat{\mu }_1/\hat{\lambda }_1}}$.

Proof

From (39) and (41) we see that $R(x,y)$ and $B(x,y)$ vanish simultaneously if and only if

$$\begin{aligned} (1-x)(\lambda _1 x -\mu )+\lambda _2(1-y)x&= 0\\ \lambda (1-x)y +\mu _2(y-x)&= 0. \end{aligned}$$

The second equation gives $x=(\lambda +\mu _2)y/((\lambda y +\mu _2))$. Plugging this value of $x$ into the first equation yields (Hint: use $\lambda =\lambda _1+\lambda _2$)

$$\begin{aligned} P_1(y):=(1-y) Q_1(y)=0 \end{aligned}$$

with $Q_1(y):=\lambda \lambda _2 (\lambda +\mu _2)y^2 +(\lambda +\mu _2-\mu )\lambda \mu _2 y -\mu \mu _2^2=0$.

From $\lim _{y\rightarrow \pm \infty }Q_1(y)=+\infty$ and $Q_1(0)=-\mu \mu _2^2$ we conclude that the polynomial $Q_1(y)$ has two real roots, $y_{-}<0<y_+$ and that $Q_1(y)<0$ for $0\le y<y_+$. Since

$$\begin{aligned} Q_1(1)=\left( \frac{\lambda +\mu _2}{\mu \mu _2}\right) \left( \frac{\lambda }{\mu }\left( 1+\frac{\lambda _2}{\mu _2}\right) -1\right) <0, \end{aligned}$$

(84)

where the latter inequality holds under conditions (34), we conclude that $Q_1(y)<0$ for $y\in [0,1]$, which in turn implies that $P_1(y)<0$ for $y\in [0,1)$. The latter completes the proof of (ii) since $[y_1,y_2]\subset [0,1)$ [see (54)].

The proof of (i) is the same as the proof of (ii) up to interchanging incides $1$ and $2$.

Eqns (iii) and (iv) both follow from the fact that $k([y_1,y_2]) =C_{\sqrt{\hat{\mu }_1/\hat{\lambda }_1}}$ (cf. Proposition 3-(11)) and the relation $h(k(y))=y$ for $y\in [y_1,y_2]$ (cf. Proposition 3-(d1)). $\square$

Lemma 3

Under Convention (35), $h(x)$ is analytic for $1<|x|<\sqrt{\hat{\mu }_1/\hat{\lambda }_1}$ and continuous for $1\le |x|\le \sqrt{\hat{\mu }_1/\hat{\lambda }_1}$.

Proof

We already know by Proposition 3 that $h(x)$ is analytic for $x\in \mathbb C -[x_1,x_2]-[x_3,x_4]$ where $x_2\le 1<x_3$. It is therefore enough to show that $\sqrt{\hat{\mu }_1/\hat{\lambda }_1}<x_3$ or, equivalently from (56) that $e_{+}\left( \sqrt{\hat{\mu }_1/\hat{\lambda }_1}\right) <0$. Easy algebra shows that $e_+\left( \sqrt{\hat{\mu }_1/\hat{\lambda }_1}\right) =-\sqrt{\hat{\mu }_1/\hat{\lambda }_1} \left( \left( \sqrt{\hat{\lambda }_1}-\sqrt{\hat{\mu }_1}\right) ^2 + \left( \sqrt{\hat{\lambda }_2}+\sqrt{\hat{\mu }_2}\right) ^2\right) <0$, which concludes the proof. $\square$

Lemma 4

Assume that conditions (34) hold. Define

$$\begin{aligned} x_0:=\frac{-(\lambda +\mu _1-\mu )\lambda \mu _1+\sqrt{((\lambda +\mu _1-\mu )\lambda \mu _1)^2 + 4 \lambda \lambda _1(\lambda +\mu _1)\mu \mu _1^2}}{2\lambda \lambda _1 (\lambda +\mu _1)} >1 \end{aligned}$$

If $x_0\le \sqrt{\hat{\mu }_1/\hat{\lambda }_1}$ and if $(\lambda +\mu _1)x_0/(\lambda x_0+\mu _1)\le \sqrt{\hat{\mu }_2/\hat{\lambda }_2}$ then $A(x,h(x))$ has exactly one zero $x=x_0$ in the region $D_x:=\left\{ x\in \mathbb C : 1<|x|\le \sqrt{\hat{\mu }_1/\hat{\lambda }_1}\right\}$ and this zero has multiplicity one. Otherwise $A(x,h(x))$ has no zero in $D_x$.

Proof

From (38) and (40) we see that $R(x,y)$ and $A(x,y)$ vanish simultaneously if and only if

$$\begin{aligned} (1-y)(\lambda _2 y -\mu )+\lambda _1(1-x)y&= 0 \end{aligned}$$

(85)

$$\begin{aligned} \lambda (1-y)x +\mu _1(x-y)&= 0. \end{aligned}$$

(86)

Eq. (86) gives

$$\begin{aligned} y=\frac{(\lambda +\mu _1)x}{\lambda x +\mu _1}. \end{aligned}$$

(87)

Plugging this value of $y$ into (85) yields

$$\begin{aligned} \frac{1-x}{(\lambda x +\mu _1)^2}\,Q_2(x)=0 \end{aligned}$$

with $Q_2(x):=\lambda \lambda _1 (\lambda +\mu _1) x^2 +(\lambda +\mu _1-\mu ) \lambda \mu _1 x -\mu \mu _1^2$.

Therefore, $A(x,h(x))$ will vanish in the region $D_x$ if and only if the polynomial $Q_2(x)$ vanishes in $D_x$. From $\lim _{x\rightarrow \pm \infty }Q_2(x)=+\infty$, $Q_2(0)=\mu \mu _1^2 <0$ and

$$\begin{aligned} Q_2(1)=\mu \mu _1 (\lambda +\mu _1) \left( \frac{\lambda }{\mu }+ \frac{\lambda \lambda _1}{\mu \mu _1}-1\right) < 0 \end{aligned}$$

(88)

we conclude that $Q_2(x)$ has always two real zeros with opposite sign.

Let us first focus on the negative zero of $Q_2(x)$, denoted by $x_{-}$. Let us show that $x_-$ cannot belong to the region $D_x$ or, equivalently, that $x_{-}$ cannot satisfies the inequalities $-\sqrt{\hat{\mu }_1/\hat{\lambda }_1}\le x_{-}<-1$. Assume that $-\sqrt{\hat{\mu }_1/\hat{\lambda }_1}\le x_{-}<-1$ and that $A(x_{-},h(x_{-}))=0$. By (40) the latter equality implies (Hint: $R(x_{-},h(x_{-}))=0$ by definition of $h(x)$)

$$\begin{aligned} \lambda \mu (1-h(x_{-}))x_{-} +\mu \mu _1 (x_{-}-h(x_{-}))=0. \end{aligned}$$

(89)

Since $-1\le h(x_{-})\le 1$ from Proposition 3-(e), we observe that $(1-h(x_{-}))x_{-} \le 0$ and $(x_{-}-h(x_{-}))<0$ so that the l.h.s. of (89) cannot be equal to zero. Therefore, $A(x),h(x))$ does not vanish at $x=x_{-}$.

We now focus on the positive zero of $Q_2(x)$, denoted by $x_0$. Note that $x_0>1$ from (88). If $x_0> \sqrt{\hat{\mu }_1/\hat{\lambda }_1}$ then clearly $A(x,h(x))$ has no zero in $(1, \sqrt{\hat{\mu }_1/\hat{\lambda }_1}]$. If $1<x_0 \le \sqrt{\hat{\mu }_1/\hat{\lambda }_1}$ then $A(x,h(x))$ as a unique zero in $(1, \sqrt{\hat{\mu }_1/\hat{\lambda }_1}]$, given by $x=x_0$, provided that [see (87)] $h(x_0)=(\lambda +\mu _1)x_0/(\lambda x_0+\mu _1)\le \sqrt{\hat{\mu }_2/\hat{\lambda }_2}$ since we know from Proposition 3-(b2) that the branch $h(x)$ is such that $|h(x)|\le \sqrt{\hat{\mu }_2/\hat{\lambda }_2}$ for all $x\in \mathbb C$; if $(\lambda +\mu _1)x_0/(\lambda x_0+\mu _1)>\sqrt{\hat{\mu }_2/\hat{\lambda }_2}$ then $A(x,h(x))$ does not vanish in $(1, \sqrt{\hat{\mu }_1/\hat{\lambda }_1}]$.

We are left with proving that when $A(x,h(x))$ vanishes at $x=x_0$ then this zero has multiplicity one. From now on we assume that $A(x_0,h(x_0))=0$.

From the definition of $h(x)$ and (40) we get

$$\begin{aligned} 0=R(x,h(x))=\frac{\alpha }{\mu _2} A(x,h(x))+\mu [\lambda (1-h(x))x +\mu _1(x-h(x))]. \end{aligned}$$

Differentiating this equation w.r.t. $x$ gives

$$\begin{aligned} 0=\frac{\alpha }{\mu _2} \frac{dA(x,h(x))}{\text {d}x} +\mu [-\lambda h^{\prime }(x)x +\lambda (1-h(x))+\mu _1(1-h^{\prime }(x))]. \end{aligned}$$

(90)

Assume that $dA(x,h(x))/\text {d}x=0$ at point $x=x_0$, namely, assume that $A(x,h(x))$ has a zero of multiplicity at least two at $x=x_0$. From (90) this implies

$$\begin{aligned} -\lambda h^{\prime }(x_0)x_0 +\lambda (1-h(x_0))+\mu _1(1-h^{\prime }(x_0)=0 \end{aligned}$$

that is

$$\begin{aligned} h^{\prime }(x_0)=\mu _1 \frac{\lambda +\mu _1}{(\lambda x_0+\mu _1)^2} \end{aligned}$$

(91)

with $h(x_0)=(\lambda +\mu _1)x_0/(\lambda x_0+\mu _1)$ [see (87)].

On the other hand, letting $(x,y)=(x,h(x))$ in (38) yields

$$\begin{aligned} A(x,h(x))= ((1-h(x))(\lambda _2 h(x)-\mu )+\lambda _1 (1-x)h(x))\mu _2 x. \end{aligned}$$

(92)

Differentiating $A(x,h(x)$ wrt $x$ in (92) and letting $x=x_0$ gives

$$\begin{aligned} \frac{\text {d}A(x,h(x))}{\text {d}x}|_{x=x_0}&= [ -h^{\prime }(x_0) (\lambda h(x_0)-\mu )+\lambda _2(1-h(x_0))h^{\prime }(x_0) \\&-\lambda _1 h(x_0)+\lambda _1(1-x_0)h^{\prime }(x_0)]\mu _2 x_0 \\&+ \frac{\mu _2}{x_0}A(x_0,h(x_0))\\&= [h^{\prime }(x_0)(-2\lambda _2 h(x_0)+\lambda _2+\mu +\lambda _1(1-x_0))-\lambda _1 h(x_0)]\mu _2 x_0 \\&+ \frac{\mu _2}{x_0}A(x_0,h(x_0))\\&= [h^{\prime }(x_0)(-2\lambda _2 h(x_0)+\lambda _2+\mu +\lambda _1(1-x_0))-\lambda _1 h(x_0)]\mu _2 x_0 \end{aligned}$$

since $A(x_0,h(x_0))=0$. Therefore, $dA(x,h(x))/\text {d}x=0$ at point $x=x_0$ iff (note that $x_0\not =0$)

$$\begin{aligned} h^{\prime }(x_0)(-2\lambda _2 h(x_0)+\lambda _2+\mu +\lambda _1(1-x_0))-\lambda _1 h(x_0)=0. \end{aligned}$$

Since $-2\lambda _2 h(x_0)+\lambda _2+\mu +\lambda _1(1-x_0)<0$ because $x_0>1$, we get

$$\begin{aligned} h^{\prime }(x_0)=\frac{\lambda _1 h(x_0)}{-2\lambda _2 h(x_0)+\lambda _2+\mu +\lambda _1(1-x_0)} \end{aligned}$$

with [see (87)] $h(x_0)=(\lambda +\mu _1)x_0/(\lambda x_0+\mu _1)$, so that $h^{\prime }(x_0)<0$. However, $h^{\prime }(x_0)>0$ in (91). This yields a contradiction, thereby implying that $dA(x,h(x))/\text {d}x$ does not vanish at point $x=x_0$ when $A(x,h(x))$ does or, equivalently, that $x_0$ is a zero of multiplicity one. $\square$

Lemma 5

Under conditions (34) and Convention (35) the index $\chi$ of the Riemann–Hilbert problem (the index is defined in (68)) is equal to zero.

Proof

Recall the definition of $U(x)$ in (65). First, by studying $U(\sqrt{\hat{\mu }_1/\hat{\lambda }_1}e^{i\theta })$ for $\theta \in [0,2\pi )$ it is easily seen that $U(x)$ describes a closed (and simple) contour when $x$ describes the circle $C_{\sqrt{\hat{\mu }_1/\hat{\lambda }_1}}$; moreover, for $x\in C_{\sqrt{\hat{\mu }_1/\hat{\lambda }_1}}, U(x)$ takes only real values when $x\in \{- \sqrt{\hat{\mu }_1/\hat{\lambda }_1}, \sqrt{\hat{\mu }_1/\hat{\lambda }_1}\}$.

As a result, we will show that $\chi =0$ if we show that

$$\begin{aligned} U\left( -\sqrt{\hat{\mu }_1/\hat{\lambda }_1}\right) \times U\left( \sqrt{\hat{\mu }_1/\hat{\lambda }_1}\right) >0, \end{aligned}$$

(93)

since (93) will imply that the contour defined by $\{U(x): |x|=\sqrt{\hat{\mu }_1/\hat{\lambda }_1}\}$ does not contain the point $x=0$ in its interior, so that by definition of the index, $\chi =0$.

We have from (40)–(41) (Hint: $R(x,h(x))=0$ by definition of $h(x))$)

$$\begin{aligned} A(x,h(x))&= -\frac{\mu \mu _2}{\alpha } (\lambda (1-h(x))x +\mu _1(x-h(x)) \end{aligned}$$

(94)

$$\begin{aligned} B(x,h(x))&= -\frac{\mu \mu _1}{\alpha } (\lambda (1-x)h(x) +\mu _2(h(x)-x)). \end{aligned}$$

(95)

Define $x_{-}:=- \sqrt{\hat{\mu }_1/\hat{\lambda }_1}$ and $x_{+}:= \sqrt{\hat{\mu }_1/\hat{\lambda }_1}$.

By Convention (35) we know that $x_{-}<-1$ and $x_{+}>1$. Also note that $h(x_{-})=y_1<1$ and $h(x_{+})=y_2<1$ from Proposition 3-(d2) and (54). With this, it it is easily seen from (94)–(95) that

$$\begin{aligned} A(x_{-},h(x_{-}))>0 \quad \hbox {and}\quad A(x_{+},h(x_{+}))<0 \end{aligned}$$

and

$$\begin{aligned} B(x_{-},h(x_{-}))<0 \quad \hbox {and}\quad B(x_{+},h(x_{+}))>0 \end{aligned}$$

so that

$$\begin{aligned} A(x_{-},h(x_{-}))/B(x_{-},h(x_{-}))<0 \quad \hbox {and}\quad (A(x_{+},h(x_{+}))/B(x_{+},h(x_{+}))<0. \end{aligned}$$

and, therefore,

$$\begin{aligned} A(x_{-},h(x_{-}))/B(x_{-},h(x_{-}))\,A(x_{+},h(x_{+}))/B(x_{+},h(x_{+}))>0. \end{aligned}$$

(96)

The above shows that (93) is true if $r=0$ in the definition of $U(x)$ since in this case $U(x)=A(x,h(x))/B(x,h(x))$.

Assume that $r=1$ in the definition of $U(x)$ with $x_0<x_+$ and $(\lambda +\mu _1)x_0/(\lambda x_0+\mu _1)\le \sqrt{\hat{\mu }_2/\hat{\lambda }_2}$. Since $(x-x_0)<0$ for $x=x_{-}$ and $(x-x_0)>0$ for $x=x_{+}$ we conclude from (96) that $U(x_-)>0$ and $U(x_+)>0$, thereby showing that (93) is also true in this case.

It remains to investigate the case when $r=1$ with $x_0=x_+$ and $(\lambda +\mu _1)x_0/(\lambda x_0+\mu _1)\le \sqrt{\hat{\mu }_2/\hat{\lambda }_2}$. Clearly, $U(x_{-})>0$ since, from (96), $A(x_{-},h(x_{-}))/B(x_{-},h(x_{-}))<0$ and $(x_{-}-x_{0})<0$ because $x_{-}<-1$.

Let us focus on the sign of $U(x_{+})$. We know that the mapping $x\rightarrow U(x)$ is continuous for $|x|\le x_{+}$ and that $U(x_+)\not =0$ when $x_+=x_0$. Since we have shown that $U(x_{+})>0$ when $x_0<x_+$ and $(\lambda +\mu _1)x_0/(\lambda x_0+\mu _1)\le \sqrt{\hat{\mu }_2/\hat{\lambda }_2}$, we deduce, by continuity, that necessarily $U(x_+)>0$ when $x_{+}=x_0$ and $(\lambda +\mu _1)x_0/(\lambda x_0+\mu _1)\le \sqrt{\hat{\mu }_2/\hat{\lambda }_2}$, which concludes the proof. $\square$

Lemma 6

Under condition (34) and Convention (35), $B(k(y),y)\not =0$ for $|y|=1, y\not =1$. Also, $B(k(y),y)$ has a zero at $y=1$, with multiplicity one.

Proof

Fix $|y|=1, y\not = 1$. We know from Proposition 3-(a1) that $|k(y)|<1$.

From (41) and the fact that $R(k(y),y)=0$ by definition of $k(y)$, we see that $B(k(y),y)=0$ is equivalent to

$$\begin{aligned} 0=\lambda (1-k(y))y+\mu _2(y-k(y))=(\lambda (1-k(y))+\mu _2) y - \mu _2 k(y) \end{aligned}$$

that is,

$$\begin{aligned} \lambda (1-k(y)+\mu _2) y=\mu _2 k(y). \end{aligned}$$

Taking the absolute value in both sides of the above equation yields

$$\begin{aligned} |\lambda (1-k(y)+\mu _2)|= |\lambda (1-k(y)+\mu _2)y|=|\mu _2 k(y)|<\mu _2. \end{aligned}$$

(97)

But $|\lambda (1-k(y))+\mu _2)|>\mu _2$ which contradicts (97). Hence, $B(k(y),y)\not =0$ for $|y|=1, y\not =1$.

Since $k(1)=1$, we see that $B(k(1),1)=B(1,1)=0$ from the definition of $B(x,y)$. Let us show that the multiplicity of this zero is one. This amounts to showing that $\text {d}B(k(y),y)/\text {d}y$ does not vanish at $y=1$.

Differentiating $B(k(y),y)$ w.r.t. $y$ in (41) (Hint: $R(k(y),y)=0$) and setting $y=1$, gives

$$\begin{aligned} \frac{\text {d}B(k(y),y)}{\text {d}y}|_{y=1}=\frac{\mu \mu _1}{\alpha } ((\lambda +\mu _2)k^{\prime }(1)-\mu _2). \end{aligned}$$

(98)

Let us calculate $k^{\prime }(1)$, the derivative of $k(y)$ at $y=1$. To this end, let us use (37) to differentiate $R(k(y),y)$ (which is equal to zero) w.r.t. $y$, which gives

$$\begin{aligned} 0=\frac{\text {d} R(k(y),y)}{\text {d}y}|_{y=1}=(\mu \mu _1 -\alpha \lambda _1)k^{\prime }(1)+\mu \mu _2 -\alpha \lambda _2 \end{aligned}$$

(99)

so that $k^{\prime }(1)=(\alpha \lambda _2-\mu \mu _2)/(\mu \mu _1 -\alpha \lambda _1)$ (note that $\mu \mu _1 -\alpha \lambda _1\not =0$ from Convention (35), which shows that $k'(1)$ is well defined). Plugging this value of $k'(1)$ into (98) gives

$$\begin{aligned} \frac{\text {d}B(k(y),y)}{\text {d}y}|_{y=1}&= \frac{\mu \mu _1}{\alpha (\mu \mu _1-\alpha \lambda _1)}\, ((\alpha \lambda _2-\mu \mu _2)(\lambda +\mu _2)-\mu _2(\mu \mu _1 -\alpha \lambda _1))\\&= \frac{\mu \mu _1}{\alpha (\mu \mu _1 -\alpha \lambda _1)}\alpha (\lambda \lambda _2 +\lambda \mu _2 -\mu \mu _2)\\&= \frac{\mu \mu _1}{\mu \mu _1 -\alpha \lambda _1}\mu \mu _2\left( \frac{\lambda \lambda _2}{\mu \mu _2}+\frac{\lambda }{\mu } -1\right) <0 \end{aligned}$$

under the conditions in (34) (to establish the 2nd equality we have used the definitions of $\alpha$ and $\lambda$). This proves that $\text {d}B(k(y),y)/\text {d}y|_{y=1}\not =0$ and completes the proof. $\square$