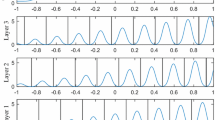
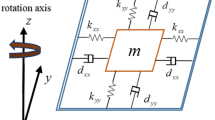
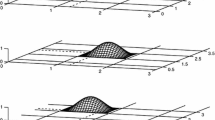
Abstract
The cerebellar model articulation controller (CMAC) neural network is an associative memory that is biologically inspired by the cerebellum, which is found in the brains of animals. In recent works, the kernel recursive least squares CMAC (KRLS–CMAC) was proposed as a superior alternative to the standard CMAC as it converges faster and does not require tuning of a learning rate parameter. One improvement to the standard CMAC that has been discussed in the literature is eligibility, and vector eligibility. With vector eligibility the CMAC is able to control online motion control problems that it could not previously, stabilize the system much faster, and converge to a more intelligent solution. This paper integrates vector eligibility with the KRLS–CMAC and shows how the combination is advantageous through two simulated control experiments.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Albus JS (1975) New approach to manipulator control: the cerebellar model articulation controller (CMAC). J Dyn Syst Meas Control Trans ASME Ser G 3:220–227. doi:10.1115/1.3426922
Albus JS (1975) Data storage in the cerebellar model articulation controller (CMAC). J Dyn Syst Meas Control Trans ASME Ser G 3:228–233
Gomi H, Kawato M (1990) Learning control for a closed loop system using feedback-error-learning. In: Proceedings of the 29th IEEE conference on decision and control, 5–7 Dec 1990, vol 3286, pp 3289–3294. doi:10.1109/cdc.1990.203403
Laufer C, Coghill G (2011) Efficient recursive least squares methods for the CMAC neural network. Int J Mach Learn Comput 1(1):20–29
Qin T, Chen Z, Zhang H, Li S, Xiang W, Li M (2004) A learning algorithm of CMAC based on RLS. Neural Process Lett 19(1):49–61. doi:10.1023/b:nepl.0000016847.18175.60
Engel Y, Mannor S, Meir R (2004) The kernel recursive least-squares algorithm. IEEE Trans Signal Process 52(8):2275–2285. doi:10.1109/tsp.2004.830985
Malaka R, Hammer M (1996) Real-time models of classical conditioning. In: IEEE international conference on, neural networks, 3–6 June 1996, vol 762, pp 768–773. doi:10.1109/icnn.1996.548993
Collins D, Wyeth GF (1999) Cerebellar control of a line following robot. In: Proceedings of the Australian conference on robotics and automation, pp 74–79. doi:http://espace.library.uq.edu.au/view/UQ:149920
Smith RL (1998) Intelligent motion control with an artificial cerebellum. University of Auckland, Auckland
Parks PC, Militzer J (1991) Improved allocation of weights for associative memory storage in learning control systems. In: 1st IFAC symposium on design methods of control systems, pp 777–782
Horvath G, Szabo T (2007) Kernel CMAC with improved capability. Syst Man Cybern B 37(1):124–138. doi:10.1109/tsmcb.2006.881295
Lin CS, Kim H (1991) CMAC-based adaptive critic self-learning control. IEEE Trans Neural Netw 2(5):530–533. doi:10.1109/72.134290
Lin CS, Kim H (1995) Selection of learning parameters for CMAC-based adaptive critic learning. IEEE Trans Neural Netw 6(3):642–647. doi:10.1109/72.377969
Främling K (2007) Replacing eligibility trace for action-value learning with function approximation. In: Proceedings of the 15th European symposium on artificial, neural networks, 25–27 April 2007, pp 313–318. doi:http://www.researchgate.net/publication/221165995_Replacing_eligibility_trace_for_action-value_learning_with_function_approximation
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Laufer, C., Patel, N. & Coghill, G. The Kernel Recursive Least Squares CMAC with Vector Eligibility. Neural Process Lett 39, 269–284 (2014). https://doi.org/10.1007/s11063-013-9303-z
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11063-013-9303-z