Skip to main content
SpringerLink
Log in

Numerical calculation of temperature and surface topology during a laser ablation process for ceramic coatings

  • Computational Micromechanics of Materials
  • Published:
Meccanica Aims and scope Submit manuscript

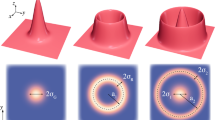
Abstract

In this paper a numerical procedure is presented to calculate a laser ablation process for ceramic thick film coatings. The code is required to cover temperature dependent material data, projected beam intensities and inhomogeneous coating–substrate combinations to calculate the hole shape geometry, the temperature distribution under the surface and the ablation rate per pulse. Therefore, the ablation speed was calculated by an Arrhenius equation while the temperature distribution was simulated by means of the heat conduction equation, which is solvable by a finite differences scheme. Hence, an adaptive mesh is used and the expansion of the code to three spatial dimensions enables the simulation of more complex ablation geometries. The simulation time was held low by introducing actualization frequencies, where critical and time consuming steps were only run if necessary. A validation of the numerical simulation was done by comparing the calculated temperature depth distribution and hole geometry with micrographs of experimental ablations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  1. Wenzelburger M, Lopez D, Gadow R (2006) Methods and application of residual stress analysis on thermally sprayed coatings and layer composites. Surf Coat Technol 201(5):1995–2001

    Article  Google Scholar 

  2. Weidmann P, Weber U, Schmauder S, Martinez Garcia V (2014) Investigation of influence factors on residual stress determination within coated surfaces in consideration of the differential and integral method. Adv Mater Res 996:307–312

    Article  Google Scholar 

  3. Lorazo P, Lewis LJ, Meunier M (2006) Thermodynamic pathways to melting, ablation, and solidification in absorbing solids under pulsed laser irradiation. Phys Rev 73(134108):1–22

    Google Scholar 

  4. Ruf A (2004) Laser in der Materialbearbeitung. Herbert Utz Verlag München

  5. Modest MF (2006) Effects of multiple reflections on hole formation during short-pulsed laser drilling. J Heat Transf 128:653–661

    Article  Google Scholar 

  6. Eichler J, Eichler HJ (2010) Laser Bauformen, Strahlführung. Anwendungen. Springer, New York

    Google Scholar 

  7. Callies G (1999) Modellierung von qualitats- und effektivitätsbestimmenden Mechanismen beim Laserabtragen. PhD thesis, Univeristät Stuttgart

  8. Araya G, Gutierrez G (2006) Analytical solution for a transient, three-dimensional temperature distribution due to a moving laser beam. Int J Heat Mass Transf 49(21–22):4124–4131

    Article  MATH  Google Scholar 

  9. Ho CY, Lu JK (2003) A closed form solution for laser drilling of silicon nitride and alumina ceramics. J Mater Process Technol 140(1–3):260–263

    Article  Google Scholar 

  10. Roy S, Modest MF, Bang SY (1993) Cw laser machining of hard ceramics. Int J Heat Mass Transf 36(14):3515–3540

    Article  Google Scholar 

  11. Modest MF (1996) Three-dimensional, transient model for laser machining of ablating/decomposing materials. Int J Heat Mass Transf 39(2):221–234

    Article  Google Scholar 

  12. Tannehill JC, Anderson DA, Pletcher RH (1997) Computational fluid mechanics and heat transfer. Taylor & Francis, Washingto

    Google Scholar 

  13. Anisimov SI, Lukyanchuk BS (2002) Selected problems of laser ablation theory. Phys Usp 45(3):293–324

    Article  ADS  Google Scholar 

  14. Carslaw HS, Jaeger JC (1959) Conduction of heat in solids. Oxford University Press, Oxford

    Google Scholar 

  15. Dubey AK, Yadava V (2008) Laser beam machining—a review. Int J Mach Tools Manuf 48(6):609–628

    Article  Google Scholar 

  16. Kabelac S, Kind M, Martin H, Mewes D, Schaber K, Stephan P (2006) VDI-Wärmeatlas. Springer, New York

    Google Scholar 

  17. Schwarz T (1996) Beitrag zur Eigenspannungsermittlung an isotropen, anisotropen sowie inhomogen, schichtweise aufgebauten Werkstoffen mittels Bohrlochmethode und Ringkernverfahren. PhD thesis, Univeristät Stuttgart

  18. Ajovalasit A, Petrucci G, Zuccarello B (1996) Determination of nonuniform residual stresses using the ring-core method. Trans ASME 118:224–228

    Google Scholar 

Download references

Acknowledgments

This work was supported by the German Research Foundation (Deutsche Forschungs Gemeinschaft, DFG) under Grant Nos. Schm 746/120 and OS 111/37.

Author information

Authors and Affiliations

  1. Institute for Materials Testing, Materials Science and Strength of Materials, University of Stuttgart, Pfaffenwaldring 32, 70569, Stuttgart, Germany

    Peter Weidmann, Ulrich Weber & Siegfried Schmauder

  2. Institute of Applied Optics, University of Stuttgart, Pfaffenwaldring 9, 70569, Stuttgart, Germany

    Giancarlo Pedrini & Wolfgang Osten

Authors
  1. Peter Weidmann
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ulrich Weber
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Siegfried Schmauder
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Giancarlo Pedrini
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Wolfgang Osten
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Peter Weidmann.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Weidmann, P., Weber, U., Schmauder, S. et al. Numerical calculation of temperature and surface topology during a laser ablation process for ceramic coatings. Meccanica 51, 279–289 (2016). https://doi.org/10.1007/s11012-015-0220-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-015-0220-2

Keywords

Search

Navigation