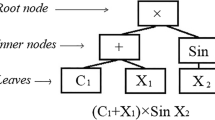
Abstract
Water level forecasting using recorded time series can provide a local modelling capability to facilitate local proactive management practices. To this end, hourly sea water level time series are investigated. The records collected at the Hillarys Boat Harbour, Western Australia, are investigated over the period of 2000 and 2002. Two modelling techniques are employed: low-dimensional dynamic model, known as the deterministic chaos theory, and genetic programming, GP. The phase space, which describes the evolution of the behaviour of a nonlinear system in time, was reconstructed using the delay-embedding theorem suggested by Takens. The presence of chaotic signals in the data was identified by the phase space reconstruction and correlation dimension methods, and also the predictability into the future was calculated by the largest Lyapunov exponent to be 437 h or 18 days into the future. The intercomparison of results of the local prediction and GP models shows that for this site-specific dataset, the local prediction model has a slight edge over GP. However, rather than recommending one technique over another, the paper promotes a pluralistic modelling culture, whereby different techniques should be tested to gain a specific insight from each of the models. This would enable a consensus to be drawn from a set of results rather than ignoring the individual insights provided by each model.










Similar content being viewed by others
References
Australian National Tide Tables (2003) Australian Hydrographic Publication 11, Department of Defence, pp. 404
Banzhaf W, Nordin P, Keller PE, Francone FD (1998) Genetic programming. Morgan Kaufmann, San Francisco
Borelli A, De Falco I, Della CA, Nicodemi M, Trautteur G (2006) Performance of genetic programming to extract the trend in noisy data series. Physica A 370:104–108
Cellucci CJ, Albano AM, Rapp PE (2003) Comparative study of embedding methods. Physical Review E Vol. 67, No. 6: 66210
EA (2004), Best Practice in Coastal Flood Forecasting, R&D Technical Report FD2206/TR1, or HR Wallingford Report TR 132 (http://evidence.environment-agency.gov.uk/FCERM/Libraries/FCERM_Project_Documents/FD2206_3912_TRP_pdf.sflb.ashx)
Farmer DJ, Sidorowich JJ (1987a) Predicting chaotic time series. Phys Rev Lett 59:845–848
Farmer DJ, Sidorowich JJ (1987b) Exploiting chaos to predict the future and reduce noise. In: Lee YC (ed) Evolution, learning and cognition. World Scientific, River Edge, pp 277–330
Ferreira C (2001a) Gene expression programming in problem solving. In: 6th Online World Conference on Soft computing in Industrial Applications (invited tutorial)
Ferreira C (2001b) Gene expression programming: a new adaptive algorithm for solving problems. Complex Syst 13(2):87–129
Fraser AM, Swinney HL (1986) Independent coordinates for strange attractors from mutual information. Physical Rev A 33(2):1134–1140
Gaur S, Deo MC (2008) Real-time wave forecasting using genetic programming. Ocean Engineering 35(11–12):1166–1172
Ghorbani MA, Khatibi R, Aytek A, Makarynskyy O, Shiri J (2010) Sea water level forecasting using genetic programming and comparing the performance with artificial neural networks. J Comput Geosci 36(5):620–627
Goldberg DE (1989) Genetic algorithms in search, optimization, and machine learning. Addison-Wesley, Reading
Grassberger P, Procaccia I (1983) Characterization of strange attractors. Phys Rev Lett 50(5):346–349
Hawkes P, Khatibi R and Sayers P. Coastal flood forecasting: best practice in England and Wales, ICCE Conference, 2004, Portugal
Hegger R, Kantz H, Schreiber T (1999) Practical implementation of nonlinear time series methods: the TISEAN package. Chaos 9:413–435
Itoh K (1995) A method for predicting chaotic time-series with outliers. Electron Commun Jpn 78(5):44–53
Kalra R, Deo MC (2007) Genetic programming for retrieving missing information in wave records along the west coast of India. Appl Ocean Res 29(3):99–111
Kennel M, Brown R, Abarbanel HDI (1992) Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys Rev A 45:3403–11
Khatibi R, Gouldby B, Sayers P, McArthur J, Roberts I, Grime A, Akhondi-asl A (2003) Improving coastal flood forecasting services of the Environment Agency, published in the Proc. of the 1st International Conference on Coastal Management, Brighton, UK (McInnes RG (ed)), pp 70–82
Koçak K (1997) Application of local prediction model to water level data. A satellite conference to the 51st ISI Session in Istanbul, Turkey. Water and Statistics, Ankara, Turkey, 185–193
Koza JR (1992) Genetic programming: on the programming of computers by means of natural selection. MIT, Cambridge
Lee HX, Han D (2005) Exploration of neuro-fuzzy models in real time flood forecasting, Proceedings of the 2008 International Conference on Artificial Intelligence and Pattern Recognition, 264-268, ISBN: 978-1-60651-000-1, published by ISRST, 7–10 of July 2008 in Orlando, FL, USA, http://www.promoteresearch.org/2008/aipr/index.html
Lorenz EN (1969) Atmospheric predictability as revealed by naturally occurring analogues. J Atmos Sci 26:636–646
Makarynskyy O, Makarynska D, Kuhn M, Featherstone WE (2004) Predicting sea level variations with artificial neural networks at Hillarys Harbour, Western Australia. Estuar Coast Shelf Sci 61:351–360
Porporato A, Ridolfi L (1997) Nonlinear analysis of river flow time sequences. Water Resources Res 33(6):1353–1367
Rosenstein MT, Collins JJ, Deluca CJ (1993) A practical method for the calculating largest Lyapunov exponents from small datasets. Physica D 65:117–34
Sivakumar B (2009) Nonlinear dynamics and chaos in hydrologic systems: latest developments and a look forward. Stoch Environ Res Risk Assess 23(7):1027–1036. doi:10.1007/s00477-008-0265-z
Solomatine DP, Rojas CJ, Velichov S, Wust JC (2000) Chaos theory in predicting surge water levels in the Norh Sea. 4th International Conference on Hydroinformatics, Iowa, USA
Takens F (1981) In: Rand DA, Young LS (eds) Detecting strange attractors in turbulence, in Lectures Notes in Mathematics. Springer, New York
Theiler J (1986) Spurious dimension from correlation algorithms applied to limited time-series data. Phys Rev A 34:2427–2432
Ustoorikar K, Deo MC (2008) Filling up gaps in wave data with genetic programming. Marine Structures 21:177–195
Wilks DS (1991) Representing serial correlation of meteorological events and forecasts in dynamic decision-analytic models. Monthly Weather Rev 119:1640–1662
Zadeh LA (1965) Fuzzy sets. Information Control 8(3):338–353
Zaldivar JM, Strozzi F, Gutierrez E, Shepherd IM (2000) Forecasting high waters at Venice Lagoon using chaotic time series analysis and nonlinear neural networks. J Hydroinform 2:61–84
Acknowledgements
The authors would like to thank the National Tidal Centre for providing the sea level measurements and the two anonymous reviewers for their valuable suggestions, which resulted in a more technically sound and better presentation of the work.
Author information
Authors and Affiliations
Corresponding author
Additional information
Responsible Editor: Franciscus Colijn
Rights and permissions
About this article
Cite this article
Khatibi, R., Ghorbani, M.A., Aalami, M.T. et al. Dynamics of hourly sea level at Hillarys Boat Harbour, Western Australia: a chaos theory perspective. Ocean Dynamics 61, 1797–1807 (2011). https://doi.org/10.1007/s10236-011-0466-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10236-011-0466-8