Activity Propagation in a Network of Coincidence-Detecting Neurons

Abstract

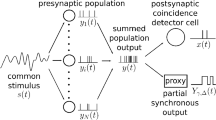
This paper presents a formal analytical description of activity propagation in a simple multilayer network of coincidence-detecting neuron models receiving and generating Poisson spike trains. Simulations are also presented. In feedforward networks of coincidence-detecting neurons, the average firing rate decreases layer by layer, until information disappears. To prevent this, the model assumes that all neurons exhibit self-sustained firing, at a preset rate, initiated by the recognition of local features of the stimulus. Such firing can be interpreted as a form of local short-term memory. Inhibitory feedback signals from higher layers are then included in the model to minimize the duration of sustained firing, while ensuring information propagation. The theory predicts the time-dependent firing probability in successive layers and can be used to fit experimental data. The analyzed multilayer neural network exhibits stochastic propagation of neural activity. Such propagation has interesting features, such as information delocalization, that could explain backward masking. Stochastic propagation is normally observed in simulations of networks of spiking neurons. One of the contributions of this paper is to offer a method for formalizing and quantifying such effects, albeit in a simplified system. The mathematical analysis produces expressions for latencies in successive layers in dependence of the number of inputs of a neuron, the level of sustained firing, and the onset time jitter in the first layer of the network. In this model, latencies are not caused by the neuronal integration time, but by the waiting time before a coincidence of input spikes occurs. Numerical evaluation indicates that the retinal jitter may make a major contribution to inter-layer visual latencies. This could be confirmed experimentally. An interesting feature of the model is its potential to describe, within a single framework, a number of apparently unrelated characteristics of visual information processing, such as latencies, backward masking, synchronization, and temporal pattern of post-stimulus histograms. Due to its simplicity, the model can easily be understood, refined, and extended. This work has its origins in the nineties, but modeling latencies and firing probabilities in realistic biological systems is still an unsolved problem.

Appendices

Appendix 1

In this appendix, we attempt to find a self-consistent solution of Eq. (17) valid for large k in the form:

$$ P_{n}(k) \approx p_1 + \varepsilon_n(k). $$

(36)

Then, under the assumption that only terms linear in the $\varepsilon_n$s need to be kept in (17), that reduces to

$$ \varepsilon_{n+1}(k) = mp_1^{m-1} \varepsilon_n(k-\tau) + (p_1 - p_1^m)mp_1^{m-1}\sum_{i=0}^{k-2}(1-p_1^m)^i \varepsilon_n(k-i-1-\tau). $$

(37)

We attempt to justify

$$ \varepsilon_{n}(k) = A_nX_1^k + B_n(k) Y_1^k, $$

(38)

where $X_1 = \overline{p_0};\, Y_1=1-p_1^m = xX_1$ and $x = \frac{1-p_1^m}{\overline{p_0}}.$

From (4), we know that $P_0(k) = p_1 P_0(f,k) + P_0(1,k) = p_1 + (p_0-p_1) \overline{p_0}^{k-1}$ so that

$$ \varepsilon_0(k) = (p_0 - p_1)\overline{p_0}^{k-1}. $$

(39)

Thereby, $A_0= \frac{p_0-p_1}{\overline{p_0}}$ and B ₀(k) = 0.

Substitution of (39) into (37) leads to

$$ \begin{aligned} \varepsilon_1(k) &= mp_1^{m-1} \left[\frac{p_0-p_1}{\overline{p_0}}\overline{p_0}^{k-\tau}+(p_1-p_1^m) \sum\limits_{i=0}^{k-2}(1-p_1^m)^i\frac{p_0-p_1}{\overline{p_0}}\overline{p_0}^{k-i-1-\tau}\right] \\ &= mp_1^{m-1} \left[\frac{p_0-p_1}{\overline{p_0}}\overline{p_0}^{k-\tau}+(p_1-p_1^m)\frac{p_0-p_1}{\overline{p_0}}\overline{p_0}^{k-1-\tau} \sum\limits_{i=0}^{k-2}x^i\right] \\ &= mp_1^{m-1} \left[A_0 X_1^k\overline{p_0}^{-\tau}+A_0(p_1-p_1^m)X_1^k\overline{p_0}^{-1-\tau} \left(\frac{1-x^{k-1}}{1-x}\right)\right] \\ &= mp_1^{m-1} \left(A_0\overline{p_0}^{-\tau} + A_0\frac{p_1-p_1^m}{1-x}\overline{p_0}^{-1-\tau}\right)X_1^k - mp_1^{m-1} \left(A_0\left(\frac{p_1-p_1^m}{1-x}\right)\overline{p_0}^{-1-\tau}\frac{1}{x}\right)Y_1^k \\ &= A_1 X_1^k + B_1 Y_1^k, \end{aligned} $$

(40)

with

$$ A_1 = mp_1^{m-1} A_0\left(\overline{p_0}^{-\tau} + \frac{p_1-p_1^m}{1-x}\overline{p_0}^{-1-\tau}\right), $$

(41)

and

$$ B_1 = - mp_1^{m-1} A_0\left(\frac{p_1-p_1^m}{1-x}\right)\frac{\overline{{cp_0}^{-1-\tau}}}{x}. $$

(42)

This process can be continued iteratively, the dependence on k of B _n (k) appearing only for k ≤ 2. We find

$$ \varepsilon_{2}(k) = A_2X_1^k + B_2(k) Y_1^k, $$

(43)

with

$$ A_2 = mp_1^{m-1} \left[x_1^{-\tau} + \frac{p_1-p_1^m}{1-x}x_1^{-1-\tau}\right]A_1, $$

(44)

and

$$ B_2(k) = mp_1^{m-1} \left[B_1 Y_1^{-\tau} - \frac{p_1-p_1^m}{1-x}\frac{A_1}{x}x_1^{-1-\tau} + (p_1-p_1^m)B_1 Y_1^{-1-\tau} (k-2)\right]. $$

(45)

In general, (38) is verified with

$$ A_{n+1} = mp_1^{m-1} x_1^{-\tau}\left[1 + \frac{p_1-p_1^m}{1-x}x_1^{-1}\right]A_n, $$

(46)

and

$$ B_{n+1}(k) = mp_1^{m-1} \left[B_n(k) Y_1^{-\tau} - \frac{p_1-p_1^m}{1-x}\frac{A_n}{x}x_1^{-1-\tau} + (p_1-p_1^m) Y_1^{-1-\tau}\sum\limits_{i=0}^{k-2}B_n(k-1-i-\tau)\right]. $$

(47)

Inspecting $B_0, B_1, B_2(k),{\ldots}$ one finds that for n > 0

$$ B_n(k) = \sum\limits_{i=0}^{n-1}\gamma_{i,n} k^i. $$

(48)

Keeping only the term with the highest power of k:

$$ B_n(k) \approx \gamma_{n-1,n} k^{n-1}, $$

(49)

where

$$ \gamma_{n-1,n} = B_1 m p_1^{m-1} (p_1 - p_1^m) Y_1^{-1-\tau}. $$

(50)

So, for large values of k and for n > 0, we obtain the approximation

$$ B_n(k) \approx B_1 \left[m p_1^{m-1} (p_1 - p_1^m) Y_1^{-1-\tau}\right]^{n-1} k^{n-1} $$

(51)

$$ \approx B_1 \beta_1^{n-1} k^{n-1}. $$

(52)

There is a similar but exact expression for A _n for n ≤ 0

$$ A_n = A_0 \left[m p_1^{m-1} \left(1 + \frac{p_1 - p_1^m}{1-x} X_1^-1\right), X_1^{-\tau}\right]^n $$

(53)

$$ = A_0 \alpha_1(x)^n $$

(54)

so that

$$ \varepsilon_n(k) \approx A_0 \alpha(x)^n \overline{p_0}^k + B_1(x) \beta_1^{n-1} x^k \overline{p_0}^k. $$

(55)

Latencies k _c are defined by

$$ P_n(k_c) = \frac{p_1}{2}, $$

(56)

or, from (36)

$$ \varepsilon_n(k_c) = - \frac{p_1}{2}. $$

(57)

To solve Eq. (55) for k _c , it is convenient to distinguish 3 domains for the values of x:

$$ \begin{aligned} I\quad &x>1\quad (1-p_1^m > \overline{p_0}). \\ II\quad &x<1\quad (1-p_1^m < \overline{p_0}). \\ III\quad &x=1\quad (1-p_1^m = \overline{p_0}). \end{aligned} $$

(58)

Reminding that p ₁ > p ₀ is required for $\varepsilon_n(k)$ to be <0, the three domains correspond to the areas marked in Fig. 9. For p ₁ < p ₀, we would observe a decrease in firing rate in post-stimulus histograms.

Domain I

For x > 1 and large values of k _c , the second term in the right-hand side of (55) is dominant:

$$ \varepsilon_n(k) \approx - B_1(x) \beta_1^{n-1} x^{k_c} \overline{p_0}^{k_c}. $$

(59)

Neglecting the term in $\ln(k_c)$ one finds

$$ k_c \approx \frac{\ln(\frac{p_1}{2}) - \ln\left(-B_1(x)\beta_1^{n-1}\right)}{\ln(1-p_1^m)}, $$

(60)

and the interlayer latency difference becomes

$$ \Updelta L_n = k_c(n) - k_c(n-1) $$

(61)

$$ \approx -\frac{\ln(\beta_1)}{\ln(1-p_1^m)} $$

(62)

$$ \approx \tau +1 - \frac{\ln(m)+(m-1)\ln(p_1) + ln(p_1-p_1^m)}{\ln(1-p_1^m)}. $$

(63)

Assuming further p ^m₁  << 1 and $\ln(p_1) \approx 0$ one gets

$$ \Updelta L_n \approx \tau +1 +\frac{\ln(m)}{(p_1^m)}. $$

(64)

Domain II

For x < 1, the second term on the right-hand side of (55) behaves as k ^n-1 _c x _{k_c} . It goes to zero for $k_c \rightarrow \infty$ and has a maximum at $k_m = (n-1)/\ln(1/m).$ Then, for the values of K _c >>K _m we have

$$ \varepsilon_n(k) \approx A_0 \alpha(x)^n \overline{p_0}^{k_c}. $$

(65)

Then,

$$ k_c \approx \frac{\ln\left(\frac{p_1}{2}\right) - \ln(-A_0) - n\ln(\alpha(x))}{\ln(\overline{p_0})}, $$

(66)

$$ \Updelta L_n \approx \tau - \frac{\ln(m)+(m-1)\ln(p_1) + \ln\left(\frac{p_1 -p_0}{p_1^m - p_0}\right)}{\ln(\overline{p_0})}. $$

(67)

In the limit $p_1 \rightarrow 1,$ (67) reduces to (24).

Domain III

For x = 1 and large k _c , the first term in the right-hand side of (55) is still dominant and we end up with same expression as in domain II.

Appendix 2

This appendix describes the simulation of the firing rate of a more realistic neuron model (than a simple coincidence detector).

Using a leaky integrate-and-fire (LIF) neuron as in Bugmann [11], partial reset to 91 % of the firing threshold. Depressing synapses were used with parameters inspired by Boudreau and Ferster [6]. The fraction of weight depressed by each input spike was 75 %. The recovery time constant was 80 ms. The somatic potential decay time constant was τ _RC = 20 ms. These values produced a reasonable fit to their Fig. 9f.

Fig. 9

Domains for the parameter x

Initial Conditions

A notable observation in Boudreau and Ferster [6] is that V1 synapses are already depressed to some degree at the start of the stimulus, due to the background activity of LGN cells. To determine what value to use, we conducted simulations using inputs firing at their average background figure of 10 Hz. The result was an asymptotic weight value of 23 % of its non-depressed value (77 % depression).

Weights for Maximal Selectivity

We then set the initial weights of a neuron with m = 25 inputs to 23 % of a value w and started the simulation with each input producing Poisson spikes trains at 200 Hz. We increased the value of w to find the value w ₁ for which the neuron started firing. We then reduced progressively the number of active inputs to find the lowest value m′ for which the neuron still responds. The selectivity S of the neuron was calculated as:

$$ S = 1 - \frac{m-m^{\prime}}{m}. $$

(68)

We then repeated the procedure for input firing rates of 200, 150, 100, 50, 25 Hz.

We found S = 0.96 for w = w ₁ and the neuron did only respond to inputs rates of 200 Hz. Each run simulated 1 s of real time to determine the average output firing rate.

Low Selectivity Regime

We then set w = 2.2w ₁ and repeated the above measurements. Table 1 summarizes the results.

Table 1 Results of simulating a low selectivity neuron

The results show that the weight value selected corresponds to a neuron with very low selectivity, able to start firing when only 44 % of inputs are active. This is plausible for visual neurons [16]. Despite such a low selectivity, the output firing rate of the neuron is always less than half of the input firing rate.

The low average hides a strong frequency peak lasting approximately 30 ms for the 200 Hz case, where the instantaneous rate is above 500 Hz. This peak is due to the larger initial EPSP sizes, despite initial depression, the low selectivity and partial reset that makes it easier for a spike to be produced immediately after a previous one.