Abstract
This paper presents a new theory of the dynamical tides of celestial bodies. It is founded on a Newtonian creep instead of the classical delaying approach of the standard viscoelastic theories and the results of the theory derive mainly from the solution of a non-homogeneous ordinary differential equation. Lags appear in the solution but as quantities determined from the solution of the equation and are not arbitrary external quantities plugged in an elastic model. The resulting lags of the tide components are increasing functions of their frequencies (as in Darwin’s theory), but not small quantities. The amplitudes of the tide components depend on the viscosity of the body and on their frequencies; they are not constants. The resulting stationary rotations (often called pseudo-synchronous) have an excess velocity roughly proportional to \(6ne^2/(\chi ^2+\chi ^{-2})\) (\(\chi \) is the mean-motion in units of one critical frequency—the relaxation factor—inversely proportional to the viscosity) instead of the exact \(6ne^2\) of standard theories. The dissipation in the pseudo-synchronous solution is inversely proportional to \((\chi +\chi ^{-1})\); thus, in the inviscid limit, it is roughly proportional to the frequency (as in standard theories), but that behavior is inverted when the viscosity is high and the tide frequency larger than the critical frequency. For free rotating bodies, the dissipation is given by the same law, but now \(\chi \) is the frequency of the semi-diurnal tide in units of the critical frequency. This approach fails, however, to reproduce the actual tidal lags on Earth. In this case, to reconcile theory and observations, we need to assume the existence of an elastic tide superposed to the creeping tide. The theory is applied to several Solar System and extrasolar bodies and currently available data are used to estimate the relaxation factor \(\gamma \) (i.e. the critical frequency) of these bodies.







Similar content being viewed by others
Notes
I will have to refer often in this paper to theories derived from Darwin’s theory. To use a simple label, I will use the word “standard Darwin theories”, or, for short, “standard theories”, to denote all Darwin-like theories in which an elastic tide is delayed by lags assumed small and proportional to frequencies.
A re-analysis of the data by Meriggiola and Iess (Meriggiola 2012) has not showed discrepancy from a synchronous motion larger than \(0.02^\circ \) per year
We use in this paper the same tide component names used for fast rotating bodies (Type I of FRH) regardless of its actual rotation speed. In next sections we use the names monthly and/or annual for tidal components with the same period as the orbital motion.
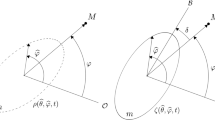
We may paraphrase one of Darwin’s statements by just changing the symbols used in it by those shown inside brackets: But because of the Earth’s viscosity, [\(\zeta \)] always tends to approach [\(\rho \)]. The stresses introduced in the Earth by the want of coincidence of [\(\zeta \)] with [\(\rho \)] vary as [\(\rho -\zeta \)]. Also the amount of flow of a viscous fluid, in a small interval of time, varies jointly as that interval and the stress. Hence the linear velocity (on the map), with which [\(\zeta \)] approaches [\(\rho \)], varies as [\(\rho -\zeta \)]. Let this velocity be [\(\gamma (\rho -\zeta )\)], where [\(\gamma \)] depends on the viscosity of the Earth, decreasing as the viscosity increases.
This does not mean that a negative mass is being assigned to void spaces; it means just that the forces included in the calculation of the equilibrium figure need to be subtracted when the masses creating them are no longer there.
Darwin (1879) used a very complete construction of the Navier–Stokes equations and, in his results, the numerical factor is 3/38 instead of 3/8. His numerical factor is determined by the spheroidal form of the tidal potential, but the intensity of the potential does not appear in the result. So, his result would hold even for an infinitesimal tide!
The subscripts used for the \(\sigma _k \) are not the same subscripts used in FRH for their homologous lags \(\varepsilon _k\).
In standard theories using Love numbers, often \(k_f\) is substituted by some smaller value to take into account the rigidity of the body. Here, a substitution of this kind is not allowed since \(k_f\) is just being used as a convenient substitute for \(A\).
In the Efroimsky–Layney regime, \(Q\) increases with the relative frequency \(\chi \) of the tide component and then increases when the critical frequency \(\gamma \) decreases.
e.g. CoRot-5 b (\(M=0.47 M_\mathrm{Jup}, e=0.09^{+0.09}_{-0.04})\), CoRoT-12 b (\(M=0.9 M_\mathrm{Jup}, e=0.07^{+0.06}_{-0.04}\)) and CoRoT-23 b (\(M=2.8 M_\mathrm{Jup}, e=0.16 \pm 0.07\))
The true longitude must be 90 degrees at the minimum light of the transit. This constraint added to the radial velocity measurements, allows a better determination of the eccentricity and the longitude of the pericenter than in the case of non-transiting planets where these parameters are to be determined based on hard-to-measure asymmetries of the radial velocity curve.
References
Alexander, M.E.: The weak friction approximation and tidal evolution in close binary systems. Astrophys. Space Sci. 23, 459–510 (1973)
Bambusi, D., Haus, E.: Asymptotic stability of synchronous orbits for a gravitating viscoelastic sphere. Celes. Mech. Dyn. Astron. 114, 255–277 (2012)
Beutler, G.: Methods of Celestial Mechanics, vol. I. Springer, Berlin (2005)
Burša, M.: Secular Love numbers of the major planets. Earth Moon Planets 59, 239–244 (1992)
Castillo-Rogez, J.C., Efroimsky, M., Lainey, V.: The tidal history of Iapetus. Spin dynamics in the light of a refined dissipation model. J. Geophys. Res. 116, E9008 (2011)
Cayley, A.: Tables of developments of functions in the theory of elliptic motion. Mem. Roy. Astron. Soc. 29, 191–306 (1861)
Chandrasekhar, S.: Ellipsoidal Figures of Equilibrium, Chap. VIII. Yale University Press, New Haven (1969)
Darwin, G.H.: On the influence of geological changes on the Earth’s axis of rotation. Philos. Trans. 167, 271–312 (1877)
Darwin, G.H.: On the bodily tides of viscous and semi-elastic spheroids and on the ocean tides upon a yielding nucleus. Philos. Trans. 170, 1–35 (1879) (repr. Scientific Papers, Cambridge, Vol. II, 1908)
Darwin, G.H.: On the secular change in the elements of the orbit of a satellite revolving about a tidally distorted planet. Philos. Trans. 171, 713–891 (1880) (repr. Scientific Papers, Cambridge, Vol. II, 1908)
Efroimsky, M., Lainey, V.: Physics of bodily tides in terrestrial planets and the appropriate scales of dynamical evolution. J. Geophys. Res. 112, E12003 (2007)
Efroimsky, M., Williams, J.G.: Tidal torques. I. A critical review of some techniques. Celes. Mech. Dyn. Astron. 104, 257–289 (2009)
Efroimsky, M.: Bodily tides near spin-orbit resonances. Celes. Mech. Dyn. Astron. 112, 283–330 (2012)
Eggleton, P.P., Kiseleva, L.G., Hut, P.: The equilibrium tide model for tidal friction. Astrophys. J. 499, 853–870 (1998)
Eggleton, P.P.: Evolutionary processes in binary and multiple stars. Cambridge University Press, Cambridge (2006)
Fernandes, S.S.: Expansions of \((r/a)^m \cos jv\) and \((r/a)^m \sin jv\) to high eccentricities. Celest. Mech. Dyn. Astron. 63, 375–408 (1996)
Ferraz-Mello, S., Sato, M.: The very-high-eccentricity asymmetric expansion of the disturbing function near resonances of any order. Astron. Astrophys. 225, 541–547 (1989)
Ferraz-Mello, S., Rodríguez, A., Hussmann, H.: Tidal friction in close-in satellites and exoplanets.The Darwin theory re-visited. Celest. Mech. Dyn. Astron. 101, 171–201 (2008) and Errata: Celest. Mech. Dyn. Astron. 104, 319–320 (2009). (ArXiv: 0712.1156 astro-ph.EP) (FRH)
Goldreich, P., Peale, S.: Spin-orbit coupling in the soalr system. Astron. J. 71, 425–438 (1966)
Greenberg, R.: Frequency dependence of tidal Q. Astron. J. 698, L42–L45 (2009)
Greenberg, R., Hoppa, G.V., Geissler, P., Sarid, A., Tufts, B.R.: The rotation of Europa. Celest. Mech. Dyn. Astron. 83, 35–47 (2002)
Greenberg, R., Weidenschilling, S.J.: How fast do Galilean satellites spin? Icarus 58, 186–196 (1984)
Hansen, B.M.S.: Calibration of equilibrium tide theory for extrasolar planetary systems. Astroph. J. 723, 285–299 (2010)
Happel, J., Brenner, H.: Low Reynolds Number Hydrodynamics. Kluwer, Dordrecht (1973)
Hoppa, G.V., Greenberg, R., Geissler, P., Tufts, B.R., Plassmann, J., Durda, D.: Rotation of Europa: constraints from terminator and limb positions. Icarus 137, 341–347 (1999)
Hurford, T.A., Sarid, A.R., Greenberg, R.: Cycloidal cracks on Europa: improved modeling and non-synchronous rotation implications. Icarus 186, 218–233 (2007)
Hut, P.: Tidal evolution in close binary systems. Astron. Astrophys. 99, 126–140 (1981)
Jackson, B., Penev, K., Barnes, R.: Constraining tidal dissipation in stars and destruction rates of exoplanets. Bull. Am. Astron. Soc. 43, # 402.06 (2011)
Jeffreys, H.: The effect of tidal friction on eccentricity and inclination. Mon. Not. R. Astron. Soc. 122, 339–343 (1961)
Karato, S.-I.: Deformation of Earth Materials. An Introduction to the Rheology of Solid Earth. Cambridge University Press, Cambridge (2008)
Kaula, W.M.: Tidal dissipation by solid friction and the resulting orbital evolution. Rev. Geophys. 3, 661–685 (1964)
Laskar, J., Correia, A.C.M.: The Rotation of Extra-solar Planets. In: Extrasolar Planets: Today and Tomorrow, ASP Conference Series, vol. 321, pp. 401–410 (2004)
Lainey, V., Arlot, J.-E., Karatekin, Ö., Van Hoolst, T.: Strong tidal dissipation in Io and Jupiter from astrometric observations. Nature 459, 959–967 (2009)
Leconte, J., Chabrier, G., Baraffe, I.: Uncertainties in tidal theory. IAU Symp. 276, 248–251 (2010)
Léger, A., Grasset, O., Fegley, B., Codron, F., Albarede, A.F., et al.: The extreme physical properties of the CoRoT-7b super-Earth. Icarus 213, 1–11 (2011)
MacDonald, G.F.: Tidal friction. Rev. Geophys. 2, 467–541 (1964)
Malmberg, D., Davies, M.B.: On the origin of eccentricities among extrasolar planets. Mon. Not. R. Astron. Soc. 394, L26–L30 (2009)
Meriggiola, R.: The Determination of the Rotational State of Celestial Bodies. Ph.D.Thesis, La Sapienza, Roma (2012)
Melchior, P.: The Tides of the Planet Earth. Pergamon Press, Oxford (1983)
Meyer, J., Wisdom, J.: Tidal heating in Enceladus. Icarus 188, 535–539 (2007)
Michtchenko, T.A., Ferraz-Mello, S.: Modeling the 5:2 mean-motion resonance in the Jupiter-Saturn planetary system. Icarus 149, 357–374 (2001)
Migaszewski, C.: The generalized non-conservative model of a 1-planet system revisited. Celest. Mech. Dyn. Astron. 113, 169–203 (2012)
Mignard, F.: The evolution of the lunar orbit revisited. I. Moon Planets 20, 301–315 (1979)
Milazzo, M.P., Geissler, P.E., Greenberg, R., et al.: Non-Synchronous Rotation of Io? Conference Jupiter: The Planet. Satellites and Magnetosphere, Boulder (2001)
Murray, C.D., Dermott, S.F.: Solar System Dynamics. Cambridge University Press, Cambridge (1999)
Ogilvie, G.I., Lin, D.N.C.: Tidal dissipation in rotating giant planets. Astrophys. J. 610, 477–509 (2004)
Ogilvie, G.I., Lin, D.N.C.: Tidal dissipation in rotating solar-type stars. Astrophys. J. 661, 1180–1191 (2007)
Oswald, P.: Rheophysics: The Deformation and Flow of Matter. Cambridge University Press, Cambridge (2009)
Rauer, H., Queloz, D., Csizmadia, S.Z., Deleuil, M., Alonso, R., et al.: Transiting exoplanets from the CoRoT space mission VII. The hot-Jupiter-type planet CoRoT-5b. Astron. Astrophys. 506, 281–286 (2009)
Ray, R.D., Eanes, R.J., Chao, B.F.: Detection of tidal dissipation in the solid Earth by satellite tracking and altimetry. Nature 381, 595–597 (1996)
Remus, F., Mathis, S., Zahn, J.-P.: The equilibrium tide in stars and giant planets. I. The coplanar case. Astron. Astrophys. 544, A.132 (2012)
Rodríguez, A., Ferraz-Mello, S., Michtchenko, T.A., Beaugé, C., Miloni, O.: Tidal decay and orbital circularization in close-in two-planet systems. Mon. Not. R. Astron. Soc. 415, 2349–2358 (2011)
Sears, W.D., Lunine, J.I., Greenberg, R.: Equilibrium nonsynchronous rotation of Titan. Icarus 105, 259–262 (1993)
Segatz, M., Spohn, T., Ross, M.N., Schubert, G.: Tidal dissipation, surface heat flow, and figure of viscoelastic models of Io. Icarus 75, 187–206 (1988)
Singer, S.F.: The origin of the Moon and geophysical consequences. Geophys. J. R. Astron. Soc. 15, 205–226 (1968)
Sohl, F., Hussmann, H., Schwentker, B., Spohn, T., Lorenz, R.D.: Interior structure models and tidal Love numbers of Titan. J. Geophys. Res. 108(E12), 5130 (2003)
Sotin, C., Choblet, G., Head, J.W., Mocquet, A., Tobie, G.: Thermal evolution of Europa’s icy crust. www.lpi.usra.edu/meetings/europa2004/pdf/7017.pdf (2004)
Stiles, B.W., Kirk, R.L., Lorenz, R.D., Hensley, S., Lee, E., et al.: Determining Titan’s Spin State from Cassini RADAR Images. Astron. J. 135, 1669–1680 (2009) and Erratum: Astron. J. 139, 311 (2011)
Tisserand, F.: Traité de Mécanique Céleste, tome II, Chap. VIII. Gauthier-Villars, Paris (1891)
Tobie, G., Grasset, O., Lunine, J.I., Mocquet, A., Sotin, C.: Titan’s internal structure inferred from a coupled thermal-orbital model. Icarus 175, 496–502 (2005)
Tokano, T., Neubauer, F.M.: Wind-induced seasonal angular momentum exchange at Titan’s surface and its influence on Titan’s length-of-day. Geophys. Res. Lett. 32(L24), 203 (2005)
Torres, G., Andersen, J., Giménez, A.: Accurate masses and radii of normal stars: modern results and applications. Astron. Astrophys. Rev. 18, 67–126 (2010)
Van Hoolst, T., Rambaux, N., Karatekin, O., Dehant, V., Rivoldini, A.: The effect of gravitational and pressure torques on Titan’s length-of-day variations. Icarus 200, 256–264 (2008)
Wahr, J.M.: Body tides on an elliptical, rotating, elastic and oceanless Earth. Geophys. J. R. Astron. Soc. 64, 677–703 (1981)
Wieczorek, M.A., Jolliff, B.L., Khan, A., et al.: The constitution and structure of the lunar interior. Rev. Miner. Geochem. 60, 221–364 (2006)
Wieczorek, M.A., Le Feuvre, M.: Did a large impact reorient the Moon? Icarus 200, 358–366 (2009)
Williams, J.G., Boggs, D.H.: Lunar Core and Mantle. What Does LLR See? In: Proceedings of the 16th Internat. Workshop on Laser Ranging (Poznan) (2008)
Williams, J.G., Boggs, D.H., Ratcliff, J.T.: Lunar Fluid Core and solid-body tides. In: Lunar and Planetary Science Conference, XXXVI, 1503.pdf (2005)
Wintner, A.: The analytical foundations of Celestial Mechanics, Princeton. (Chap, IV) (1941)
Zahn, J.P.: Les marées dans une étoile double serrée. Ann. Astrophys. 29, 313–330 (1966)
Zhang, K., Hamilton, D.P.: Orbital resonances in the inner neptunian system II. Resonant history of Proteus, Larissa, Galatea, and Despina. Icarus 193, 267–282 (2008)
Acknowledgments
I wish to acknowledge the visiting fellowship granted by the Isaac Newton Institute for Mathematical Sciences, University of Cambridge (UK), where the basic ideas of this theory were first developed. I thank Michael Efroimsky for our fruitful endless discussions about tides, rheology and dissipation, Rudi Dvorak and the Wien Universität, where parts of this paper were written, and Dr. G.Torres for kindly sending me the data used to construct Fig. 6. I am also indebted to Adrián Rodríguez and Hugo Folonier for having pointed out many mistakes in the previous versions of this paper. This investigation was supported by CNPq, grants 302783/2007-5 and 306146/2010-0.
Author information
Authors and Affiliations
Corresponding author
Appendix: Higher-order approximations
Appendix: Higher-order approximations
The eccentricity functions introduced in Sect. 3 are the Cayley expansions for the solutions of the Keplerian motion (see Cayley 1861; Fernandes 1996) corresponding to the entries \((r/a)^{-3} [\sin |\cos ] 2f\) in Cayley’s tables.
The approximations adopted in Sect. 3 may be enough for most purposes. They are certainly enough for low eccentricities. For high eccentricities, however, a different approach is necessary. Cayley expansions include in their derivation the Taylor expansion of the solution of Kepler’s equation, whose convergence radius is \(e^*=0.6627434\ldots \) (see Wintner 1941). Some simple comparisons allow us to see that for eccentricities of the order of 0.5, or even less, the results are not accurate.
Since the equations appearing in this paper are written in terms of one of the families of Cayley expansions, the power series may be substituted by Eq. 16 in the form
We may note that the function under the integral involves both the mean (\(\ell \)) and the true (\(v\)) anomalies, but can be easily handled numerically. The only difference with Eq. (16) is the preference in having the integration done over the true anomaly instead of being done over the mean anomaly (via the classical expression \(r^2 dv=a^2\sqrt{1-e^2}d\ell \)) to avoid having to solve the Kepler equation, which is operationally expensive.
The integral solves the problem of the accuracy in the determination of the Cayley coefficients (see Table 2), but not that of the Fourier series giving the variation of the elements. To obtain approximations valid in high eccentricities, it is necessary to use expansions not affected by the singularities of the Keplerian motion (see Ferraz-Mello and Sato 1989). However, one preliminary guess can be done comparing different approximations. Figure 8 shows the value of \(|\dot{e}|\) for close-in companions in pseudo-synchronous stationary rotation, in arbitrary units, considering the sum of the eccentricity-dependent terms of Eq. 49 truncated at \(N=\) 7, 20, 50 and 100, respectively. The abrupt changes of the curves with respect to the next one show a limiting eccentricity in each case. For instance the series truncated at \(N=7\) (the usual cutoff of Cayley series) give wrong results for eccentricities above 0.4. It is important to stress that the calculations showed in Fig. 5, concerning the tidal evolution predicted by the standard Darwin theory are not affected by truncation effects since for that sake we have used Mignard’s formulation whose basic equations are given in closed form (Mignard 1979) without resorting to any expansions.
\(\log |de/dt|\) obtained with the series of Eq. (49) truncated at \(N= \) 7, 20, 50 and 100. Arbitrary units
Rights and permissions
About this article
Cite this article
Ferraz-Mello, S. Tidal synchronization of close-in satellites and exoplanets. A rheophysical approach. Celest Mech Dyn Astr 116, 109–140 (2013). https://doi.org/10.1007/s10569-013-9482-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10569-013-9482-y