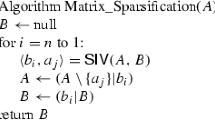Abstract
The Nullity theorem says that certain pairs of submatrices of a square invertible matrix and its inverse (known as complementary submatrices) have the same nullity. Though this theorem has been around for quite some time and also has found several applications, some how it is not that widely known. We give a brief account of the Nullity Theorem, consider its generalization to infinite dimensional spaces, called the Null Space Theorem and discuss some applications.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Bapat, R.B.: On generalized inverses of banded matrices. Electron. J. Linear Algebra 16, 284–290 (2007) (MR2349923 (2008k:15004))
Barrett, W.W.: A theorem on inverses of tridiagonal matrices. Linear Algebra Appl. 27, 211–217 (1979) (MR0545734 (80i:15003))
Ben-Israel, A., Greville, T.N.E.: Generalized Inverses, 3rd edn. Springer, New York (2003)
Bollobás, B.: Linear Analysis. Cambridge University Press, Cambridge (1990) (MR1087297 (92a:46001))
Kulkarni, S.H.: The null space theorem. Linear Algebra Appl. (2015). doi:10.1016/j.laa.2015.01.030
Limaye, B.V.: Functional Analysis, 2nd edn. New Age, New Delhi (1996) (MR1427262 (97k:46001))
Strang, G.: Linear Algebra and Its Applications, 2nd edn. Academic Press, New York (1980) (MR0575349 (81f:15003))
Strang, G., Nguyen, T.: The interplay of ranks of submatrices. SIAM Rev. 46(4), 637–646 (2004) ((electronic). MR2124679 (2005m:15015))
Acknowledgments
The author thanks Prof. Gilbert Strang and Prof. R.B. Bapat for several useful discussions.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer India
About this paper
Cite this paper
Kulkarni, S.H. (2015). The Nullity Theorem, Its Generalization and Applications. In: Romeo, P., Meakin, J., Rajan, A. (eds) Semigroups, Algebras and Operator Theory. Springer Proceedings in Mathematics & Statistics, vol 142. Springer, New Delhi. https://doi.org/10.1007/978-81-322-2488-4_12
Download citation
DOI: https://doi.org/10.1007/978-81-322-2488-4_12
Published:
Publisher Name: Springer, New Delhi
Print ISBN: 978-81-322-2487-7
Online ISBN: 978-81-322-2488-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)