Keywords

1 Introduction

The empirical Green’s function (EGF) method, proposed by Hartzell [1] and extended by Irikura [2], has been recognized as one of the most practical techniques to predict the strong idground motion produced by large earthquakes. The use of this method is limited to the case when the focal mechanism of a small event is identical or similar to that of a targeted event. On the other hand, the empirical Green’s tensor spatial derivative (EGTD) method, proposed by Plicka and Zahradnik [3], has the potential to deal with the difference in focal mechanisms between small events and a targeted event and predict the ground motion for an event with an arbitrary focal mechanism. The EGTD elements are estimated through a kind of single-station inversion using waveform data for several small events whose focal mechanisms and source time functions are well determined. This technique is expected to provide considerably accurate and stable prediction results, but discussion of its application has been limited in the literature [4–8]. In the previous studies [6, 8], considering the lowest corner frequency of about 1.0 Hz for the mainshock, we targeted 0.2–1.0 Hz band-pass-filtered velocity waveforms. In the present study, we simulate the broadband strong motions between 0.2 and 10 Hz for the same events as in the previous studies [6, 8].

1.1 Targeted Events and Stations

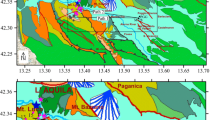
In this study, we targeted the mainshock (M J 5.4, labeled as “Event 1”) and 25 aftershocks (M J 3.1–4.7, labeled as “Events 2-26”) of the 2001 Hyogo-ken Hokubu earthquake. We used the strong motion records at the target station, HYG004, one of the K-NET stations operated by the NIED (National Research Institute for Earth Science and Disaster Prevention). The source information of these events was determined by the united hypocenter catalog of the JMA (Japan Meteorological Agency). In Fig. 8.1, we show the distribution of focal mechanisms and source time functions as well as location of the station. Details of source parameters can be found in Ohori and Hisada [8]. Data for the mainshock and 15 of the aftershocks (M J 3.5–4.7) were recorded at HYG004. As one of the K-NET stations, HYG004 was chosen as the target station because of the data quality. It is on a rock site located at the closest epicentral distance (6–10 km) from the fault zone, whose range was 4 km in the east–west direction and 6 km in the north–south direction. The observed acceleration records at HYG004 for the mainshock and 15 aftershocks were integrated into velocity waveform data with a band-pass filter of 0.2–10 Hz. To enhance the accuracy of simulation by the EGTD method, it is desirable to know the focal mechanisms and source time functions accurately as much as possible. In this study, we used the source model which was reevaluated in our previous work [6]. Among 15 events, 4 aftershock events, 3, 7, 19, 26, are excluded in the following EGTD inversion because of the relatively large discrepancy in waveform matching between the observation data and synthesis.

Fig. 8.1
figure 1

Map showing the focal mechanisms and source time functions of 16 events (mainshock and 15 aftershocks) as well as location of the station HYG004 used in present study

Full size image

1.1.1 Estimation of the EGTD

The estimation method of the EGTD has been fully explained by Ohori and Hisada [6, 8]. It is applicable to simulation of the strong motion in a frequency range below the corner frequency. Hereafter, we summarize briefly the method and provide additional explanations on how to compensate the spectral amplitude decay beyond the corner frequencies and how to simulate the broadband ground motion.

1.1.2 Basic Equations

Ground motion displacement u i (x o , t) (i = x,y,z) excited by a double-couple point source is theoretically expressed as the convolution of moment tensor elements M pq (x s ,τ) (p,q = x,y,z) and Green’s tensor spatial derivative elements G ip,q (x o , t | x s ,τ)

$$ {u}_i\left({x}_o,t\right)={M}_{pq}\left({x}_s,\tau \right)\cdot {G}_{ip,q}\left({x}_o,t\Big|{x}_s,\tau \right) $$
(8.1)

Hereafter, we abbreviate u i (x o , t), M pq (x s ,τ), and G ip,q (x o , t | x s ,τ) as u i , M pq , and G ip,q . Explicit expressions of M pq for a double-couple point source are found in the literature (e.g., Aki and Richards [9]). Considering symmetrical conditions (M pq  = M qp ) and no volume change [(M xx  = −(M yy  + M zz )] of the moment tensor elements, we can rewrite Eq. (8.1) as

$$ {u}_i={\displaystyle {\sum}_{j=1}^5{M}_j\cdot {G}_{ij}} $$
(8.2)

where M j (j = 1,2,…,5) is defined by M 1 = M xy , M 2 = M yy , M 3 = M yz , M 4 = M yz , M 5 = M zz , and G ij (j = 1,2,…,5) is defined by G i1 = G ix,y  + G iy,x , G i2 = G iy,y  − G x,x , G i3 = G iy,z  + G iz,y , G i4 = G ix,z  + G iz,x , G i5 = G iz,z  − G ix,x . In the moment tensor inversion, u i and G ij are given and M j are the unknowns to be solved in a least-squares sense. Conversely, in the EGTD inversion, u i and M j are given and G ij are the unknowns to be solved. Note that the EGTD inversion is carried out for each component at each station using data from several events simultaneously, whereas the moment tensor inversion is done for a particular event using data of all possible components at all possible stations simultaneously. It should be emphasized that the moment tensor elements are determined by the source parameters and the Green’s tensor spatial derivative elements are by the underground structure of the area surrounding the source and the station.

1.1.3 Correction of the Focal Mechanisms

The differences in source locations between the mainshock and aftershocks are significant in the EGT inversion. To compensate for this discrepancy and treat each event as a point source at the same location, we horizontally and vertically rotate the focal mechanisms, referring to the literature [4, 5]. Through the horizontal rotation, the station azimuths of the mainshock and aftershocks are set to 90 deg. as measured from north [6]; thus, the number of Green’s tensor spatial derivative elements is reduced to three (G i1 = G i4 = 0) for the radial component (i = y) and vertical component (i = z) and two (G i2 = G i3 = G i5 = 0) for the transverse component (i = x). Through the vertical rotation, the discrepancy in the takeoff angles between the mainshock and aftershocks is corrected, following the horizontal rotation. The moment tensor elements derived from focal mechanisms should be evaluated after horizontal and vertical rotations. Details of these rotations applied to focal mechanisms should be referred to Ohori and Hisada [6, 8].

1.1.4 Correction Applied to the Waveform Data

To adjust the timing between the mainshock and aftershocks, we apply a time-shift to the observation data of aftershocks to fit their S-wave arrival time with that of the mainshock. In addition, to remove the discrepancy in the source time function, we deconvolve the observation data. The observed waveforms used in the estimation of the EGTDs are corrected such that the source time function has a constant seismic moment (1.0 × 1015 Nm, nearly equal to M w 4.0) and a single-isosceles slip velocity function with a rise time of 0.32 s. It is noted that the timing between the mainshock and aftershocks and the source time function mentioned above are estimated from 0.2 to 1.0 Hz band-pass-filtered velocity waveforms. We estimated the corner frequencies of events from the records at HYG004, assuming that source spectrum obeys the ω−2 model [10]. The corner frequency of the mainshock is about 1.0 Hz, while those of 11 aftershocks are distributed in a frequency range between 1.2 and 3.0 Hz. To simulate the broadband ground motion up to the frequency beyond the corner frequency, we must remove the effect of the differences among corner frequencies. In the present study, to correct the difference in the corner frequency of each event, we assumed the scaling law based on the ω−2 model [10] and compensated the spectral amplitude decay beyond the corner frequency of each event so that we can assume that each event has the same corner frequency as that of the mainshock.

1.1.5 EGTD Estimation

The observation data for 11 aftershocks are corrected in terms of the timings, source time functions, the seismic moments, and corner frequencies, and they are inverted for the estimation of the EGTD elements. On the basis of the focal mechanisms of aftershocks rotated as mentioned above, simultaneous linear equations for each component are constructed and solved for each of the sampling data. No constraints such as smoothing or minimization for unknown parameters were included in the EGTD estimation in this study. In Fig. 8.2, we show the transverse component elements of the EGTD as example. Each element is scaled for an event with a seismic moment of 1.0 × 1015 Nm with a corner frequency of 1.0 Hz as the same of the mainshock. It is noted that as the Green’s tensor spatial derivative elements are determined not by the source characteristics but by the underground structure, the EGTD elements could be useful for the structural study in future work.

Fig. 8.2
figure 2

The EGTD elements of transverse components estimated from 11 aftershocks

Full size image

1.1.6 Simulation of the Strong Ground Motion Using the EGTD

In Fig. 8.3, we compare radial and transverse component observed velocity waveforms with a 0.2–10 Hz band-pass filtering and corresponding syntheses calculated from the EGTD. For each trace, the source time function, seismic moment, and the corner frequency of each event are taken into account. The top trace for the mainshock (Event 1) is not included in the EGTD inversion. Considering the complexity included in high-frequency components, the broadband synthesis from the EGTD reproduced acceptably the observed waveforms. Figure 8.4 shows the comparison of the maximum amplitude ratio between the synthesized velocity waveforms and observatory data. Three frequency ranges of band-pass filter are compared in Fig. 8.4: 0.2–1.0 Hz, 1.0–10 Hz, and 0.2–10 Hz. From this figure, it is found that simulation results from the EGTD show high accuracy in a frequency range of 0.2–1.0 Hz, except that the radial components of the Event 14 is somewhat overestimated. We also find that results for a frequency range of 1.0–10 Hz are acceptable. For most of the events, the maximum amplitude ratio between the synthesized velocity waveforms and observatory data is between 0.5 and 1.5. We note that results for a frequency range of 0.2–10 Hz are very similar to those of 1.0–10 Hz. On the whole, our simulation of broadband ground motion from the EGTD method reproduced successfully the observed waveforms.

Fig. 8.3
figure 3

Comparison of 0.2–10 Hz band-pass-filtered observed velocity waveforms (thick lines) and corresponding syntheses calculated from the EGTD (thin lines)

Full size image
Fig. 8.4
figure 4

Comparison of the maximum amplitude ratio between the synthesis and observatory data

Full size image

2 Conclusions

We demonstrated the applicability of the EGTD method to simulate near-field strong-motion records. In the previous studies [6, 8], considering the lowest corner frequency of about 1.0 Hz for the mainshock of the 2001 Hyogo-ken Hokubu earthquake (M J 5.4), we targeted 0.2–1.0 Hz band-pass-filtered velocity waveforms. In present study, we simulate the broadband strong motions between 0.2 and 10 Hz for the same events as in the previous studies [6, 8]. The upper limit of the target frequency range in the EGTD estimation is extended to 10 Hz, while the corner frequency of the events is in a range of 1.0 Hz to 3.0 Hz. So as to correct the discrepancy among the corner frequencies of events, we assumed the scaling law based on the ω−2 model [10] and compensated the spectral amplitude decay beyond the corner frequency. The agreement between the observed and calculated waveforms for the mainshock is satisfactory over a long duration, and there is a good match of the amplitude. To enhance the applicability of the EGTD method, further data accumulation and investigation should be required.