Keywords

1 Introduction

Many empirical equations for estimating earthquake magnitude have been developed in Japan. The most famous of these is the so-called Matsuda’s Equation [2], which is widely used for constructing seismic hazard maps of Japan (e.g., The Headquarters for Earthquake Research Promotion [3]). Matsuda’s Equation (Eq. 3.1) below is based on 14 earthquakes dated from the 1891 Nobi earthquake (MJMA 8.0: Japan Meteorological Agency magnitude) to the 1970 Southeastern Akita Prefecture earthquake (MJMA 6.2).

$$ \log\ \mathrm{L} = 0.6{\mathrm{M}}_{\mathrm{JMA}} - 2.9 $$
(3.1)

In Matsuda’s Equation, the fault parameter length L might be regarded as subsurface. On the contrary, the length of an active fault recognized on the surface from tectonic geomorphology must be used for magnitude estimation prior to the occurrence of the next earthquake. However, a problem occurs in estimating magnitudes of isolated active faults with lengths significantly shorter than the thickness of the seismogenic layer, which is estimated to be roughly 15–20 km in Japan. Thus, another empirical equation for estimating earthquake size is the following empirical equation between seismic moment Mo and fault area by Irikura and Miyake [4] as:

$$ \begin{array}{l}\mathrm{S} = 2.23\times {10}^{-15}{\mathrm{Mo}}^{2/3}\ \mathrm{f}\mathrm{o}\mathrm{r}\ \mathrm{M}\mathrm{o}<7.5\times {10}^{25}\mathrm{dyne}\hbox{-} \mathrm{cm}\\ {}\mathrm{S} = 4.24\times {10}^{-11}{\mathrm{Mo}}^{1/2}\ \mathrm{f}\mathrm{o}\mathrm{r}\ \mathrm{M}\mathrm{o}\geqq 7.5\times {10}^{25}\mathrm{dyne}\hbox{-} \mathrm{cm}\end{array} $$
(3.2)

This equation is also widely used especially in strong ground motion prediction in Japan.

However, the question of large uncertainties in the earthquake scaling relation remains in both equations. To resolve the above issues, multiple regressions are developed using world earthquake data and active fault data, and the regressions are then evaluated with AIC (Akaike’s Information Criterion, Akaike, 1974). The AIC method enables selection of the regression formula with the best fit while taking into consideration the number of parameters. By using parameters relevant to earthquakes and active faults such as stress drop, average slip rate, and recurrence interval, in the regression analysis, we develop a new empirical equation for magnitude estimation.

2 Data

The database used in this paper is compiled from the intraplate earthquake datasets listed below.

  1. 1.

    Earthquake and active fault data of Wells and Coppersmith [5]:

These data were compiled to develop empirical relationships between earthquake magnitude and various fault parameters. The data are for the years 1857–1994, and the number of data items is 244. The data fields include earthquake location, name, date, slip type, magnitude (surface wave magnitude Ms, moment magnitude Mw, seismic moment Mo), subsurface and surface rupture length, fault width, fault area, and maximum/average surface slip amount. Values thought to have low reliability are given in parentheses.

  1. 2.

    Earthquake data of Anderson et al. [6]:

These historical earthquake data were used to estimate earthquake magnitude as a function of the length and slip rate of the causative fault. The earthquake data were collected for the time period 1811–1994, and the number is 43 in total. The data fields include location, Mo, Mw, fault length, and slip rate.

  1. 3.

    Earthquake and active fault data of Mohammadioun and Serva [7]:

The characteristic aspect of this dataset is a list of variations in stress drop for different slip types, including strike-slip, normal, or reverse faults in the 1857–1994 earthquakes worldwide, plus the Umbria earthquake in 1998 (Ms 5.7), the Chi-Chi earthquake in 1999 (Ms 7.6), and the Izmit earthquake in 1999 (Ms 7.4). The number of earthquakes in the dataset is 90, and the data fields include maximum surface slip amount, static stress drop Δσ 1, dynamic stress drop Δσ 2, and the ratio of dynamic stress drop to static stress drop.

  1. 4.

    Earthquake and active fault data of Stirling et al. [8]:

The number of data items is 389, and several scaling laws are developed in this paper to compare instrumental and pre-instrumental data. The data fields include slip type, magnitude (Ms, MJMA, Mw, and Mo), minimum/maximum seismogenic fault length, minimum/maximum surface rupture length, minimum/maximum fault width, and maximum/average surface slip amount.

3 Parameters for Analysis

We first examine whether the strength of asperities on the fault plane can be quantified by the stress drop Δσ. Cotton et al. [9] showed the importance of Δσ for strong ground motion and also showed large variability of Δσ. The 90 data items for static stress drop Δσ 1 and dynamic stress drop Δσ 2 compiled from [7] are used here as stress drop Δσ. The static stress drop Δσ1 is a value calculated from the average slip amount Dave and coseismic rupture length L from geological/seismological observations with the following equation:

$$ \Delta {\sigma}_1\propto \frac{{\mathrm{D}}_{\mathrm{ave}}}{\mathrm{L}} $$
(3.3)

The dynamic stress drop Δσ 2 is a value from the spectrum of the seismic wave record.

The recurrence interval R of a fault is estimated directly from the observed displacement of layers and the dating of layers on the historical earthquake record or trench excavation results. However, this estimation is not always possible, and calculated estimation is conducted by dividing the average slip amount on the fault by the average slip rate Save as the following formula.

$$ \mathrm{R}=\frac{{\mathrm{D}}_{\mathrm{ave}}}{{\mathrm{S}}_{\mathrm{ave}}} $$
(3.4)

The average slip rate Save is also an indirect value derived from the cumulative slip amount D divided by the dating of layers/tectonic landforms T for which that slip amount was obtained.

$$ {\mathrm{S}}_{\mathrm{ave}}=\frac{\mathrm{D}}{\mathrm{T}} $$
(3.5)

The average recurrence interval R is calculated for the average slip rate Save by using the dataset of 43 earthquakes in this research (Table 3.1). However, it is difficult to estimate the average slip rate Save in Eq. (3.5) because the cumulative slip amount D is not constant along fault traces. Thus, uncertainties of slip rate might be large, and the simple mean between Smin and Smax leads to an underestimation or overestimation which is inappropriate for magnitude estimation. Therefore, just as in Anderson et al. (1996), 100 random numbers were generated in the range between Smin and Smax, and the distribution of the average slip rate Save was determined in Table 3.1 for calculation of R in Eq. (3.4).

Table 3.1 Data for multiple regression analysis compiled from [5–8]
Full size table

4 Results and Discussion

Large variances of earthquake magnitude to the same surface rupture length Ls are observed in Fig. 3.1 from [8]. Then Fig. 3.2 shows the relationship between earthquake magnitude and surface rupture length from our compiled dataset in Table 3.1. In Fig. 3.2, the dynamic stress drop Δσ 2 was divided with four marks: 50 bars or less, 50–70 bars, 70–90 bars, and 90 bars or more. According to Fig. 3.2, the stress drop is almost always 50 bars or less for earthquakes the fault length for which exceeds 100 km, though the data contain many values of 90 bars or more for fault lengths of 20 km or shorter. For fault lengths between 20 km and 100 km, in particular, near the fault length of 40 km which corresponds to an aspect ratio of two seismogenic-layer earthquakes with a large stress drop display large magnitudes, and earthquakes with a small stress drop exhibit a relatively small magnitude, even if the surface rupture length is the same. Therefore, it is possible to infer that the dynamic stress drop Δσ 2 could be an additional parameter for estimating earthquake magnitude.

Fig. 3.1
figure 1

Relationship between earthquake magnitude and surface rupture length in [8]

Full size image
Fig. 3.2
figure 2

Relationship between earthquake magnitude and surface rupture length with different marks according to stress drop in Table 3.1

Full size image

Then, a total of six variables were set for regression analysis: surface rupture length Ls, seismogenic fault length Lsub, maximum slip amount Dmax, average slip amount Dave, static stress drop Δσ 1, and dynamic stress drop Δσ 2. Single and multiple regression analyses were conducted to estimate moment magnitude Mw, and the goodness of fit arising from varying combinations of one variable, two variables and three variables were evaluated with AIC, the value of the coefficient of correlation for single regression analysis and the values of coefficient of determination (Table 3.2). Among various combinations, the Akaike’s Information Criterion [1] value was minimized by taking account of the two variables, surface rupture length Ls, and dynamic stress drop Δσ 2 as Eq. (3.6), though the coefficient of correlation between Ls andΔσ 2 shows 0.69, which means that some multicollinearity effects are assumed.

Table 3.2 Comparison of goodness of fit from single and multiple regression analyses
Full size table
$$ \mathrm{M}\mathrm{w}=1.62 \log \mathrm{L}\mathrm{s}+0.76\Delta {\sigma}_2+3.07 $$
(3.6)

However, the dynamic stress drop Δσ 2 is a value obtained by the spectrum of the seismic wave record observed after the occurrence of an earthquake. Therefore, it is an inappropriate parameter for the estimation of future earthquakes. Our alternative approach is to find a proxy parameter of dynamic stress drop Δσ 2. Figures 3.3 and 3.4 show the relationship between slip rate and Δσ 2 and between recurrence interval and Δσ 2, respectively. Figure 3.3 shows that the dynamic stress drop Δσ 2 is large when the average slip rate S is small and the dynamic stress drop Δσ 2 becomes small when the average slip rate S is large. One problem arising when slip rate is used for prediction of earthquake magnitude is that the average slip rate S has a small value of 0.01–1 mm/year in the active fault catalog, and most of them that are calculated from Eq. (3.5) need age and displacement data derived from tectonic landforms in field surveys. On the other hand, the average recurrence interval R could be derived in both Eq. (3.4) and trench excavations in field surveys. Figure 3.4 shows a relationship between recurrence interval and dynamic stress drop Δσ 2 in which longer recurrence intervals correlated with larger stress drops.

Fig. 3.3
figure 3

Relationship between average slip rate and the dynamic stress drop Δσ2 in Table 3.1

Full size image
Fig. 3.4
figure 4

Relationship between recurrence interval and the dynamic stress drop Δσ2 in Table 3.1

Full size image

We next conducted regression analyses with the average recurrence interval R determined from average displacement Dave and average slip rate in Table 3.1. Moment magnitude Mw was set as the response variable, and surface rupture length Ls and average recurrence interval R were set as the explanatory variables. The following regression equation was obtained based on the average and standard deviation for each regression coefficient:

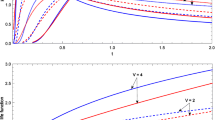
$$ \mathrm{M}\mathrm{w}=1.13 \log \mathrm{L}\mathrm{s}+0.16\Delta {\sigma}_2+4.62 $$
(3.7)

This Eq. (3.7) is then compared to Matsuda’s Equation (Eq. 3.1) in Fig. 3.5. Equation (3.7) includes the average recurrence interval R in its explanatory variables, and thus 1000, 3000, 5000, and 10,000 years are given as typical examples of the average recurrence intervals in Fig. 3.5. For surface rupture length Ls of 20 km, we find that the magnitude obtained with Eq. (3.7) is larger than Matsuda’s Equation, for all recurrence interval estimates. In contrast, the magnitude is smaller than that of Matsuda’s Equation when Ls is 80 km for average recurrence intervals of less than 3000 years and larger than Matsuda’s Equation for average recurrence intervals more than 3000 years. Furthermore, the magnitude is smaller than Matsuda’s Equation for an average recurrence interval of 1000 years or less. A difference of 0.2 in magnitude corresponds to a difference of 1000 and 10,000 years in recurrence interval. Therefore, earthquakes of different magnitude in faults of similar lengths can be explained by different recurrence intervals.

Fig. 3.5
figure 5

Comparison of the multiple regression equation in this study with different recurrence intervals and Matsuda’s Equation

Full size image

5 Summary and Conclusion

We have developed new regressions for estimating earthquake magnitude from the fault parameters such as stress drop and recurrence interval. The resulting equation was obtained. The equation shows that for a fault possessing an average recurrence interval of 1000 years or less and a length of 30 km or more, the magnitude estimated from our equation is less than that produced by Matsuda’s Equation. Conversely, the magnitude is larger than that of Matsuda for a fault length of 80 km and an average recurrence interval of 3000 years or more. A difference of 0.2 in magnitude between average recurrence intervals of 1000 years and 10,000 years was also shown.