Synthesis of Recursive ADT Transformations from Reusable Templates

Abstract

Recent work has proposed a promising approach to improving scalability of program synthesis by allowing the user to supply a syntactic template that constrains the space of potential programs. Unfortunately, creating templates often requires nontrivial effort from the user, which impedes the usability of the synthesizer. We present a solution to this problem in the context of recursive transformations on algebraic data-types. Our approach relies on polymorphic synthesis constructs: a small but powerful extension to the language of syntactic templates, which makes it possible to define a program space in a concise and highly reusable manner, while at the same time retains the scalability benefits of conventional templates. This approach enables end-users to reuse predefined templates from a library for a wide variety of problems with little effort. The paper also describes a novel optimization that further improves the performance and the scalability of the system. We evaluated the approach on a set of benchmarks that most notably includes desugaring functions for lambda calculus, which force the synthesizer to discover Church encodings for pairs and boolean operations.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Recent years have seen remarkable advances in tools and techniques for automated synthesis of recursive programs [1, 4, 8, 13, 16]. These tools take as input some form of correctness specification that describes the intended program behavior, and a set of building blocks (or components). The synthesizer then performs a search in the space of all programs that can be built from the given components until it finds one that satisfies the specification. The biggest obstacle to practical program synthesis is that this search space grows extremely fast with the size of the program and the number of available components. As a result, these tools have been able to tackle only relatively simple tasks, such as textbook data structure manipulations.

Syntax-guided synthesis (SyGuS) [2] has emerged as a promising way to address this problem. SyGuS tools, such as Sketch [18] and Rosette [20, 21] leverage a user-provided syntactic template to restrict the space of programs the synthesizer has to consider, which improves scalability and allows SyGus tools to tackle much harder problems. However, the requirement to provide a template for every synthesis task significantly impacts usability.

This paper shows that, at least in the context of recursive transformations on algebraic data-types (ADTs), it is possible to get the best of both worlds. Our first contribution is a new approach to making syntactic templates highly reusable by relying on polymorphic synthesis constructs (PSCs). With PSCs, a user does not have to write a custom template for every synthesis problem, but can instead rely on a generic template from a library. Even when the user does write a custom template, the new constructs make this task simpler and less error-prone. We show in Sect. 4 that all our 23 diverse benchmarks are synthesized using just 4 different generic templates from the library. Moreover, thanks to a carefully designed type-directed expansion mechanism, our generic templates provide the same performance benefits during synthesis as conventional, program-specific templates. Our second contribution is a new optimization called inductive decomposition, which achieves asymptotic improvements in synthesis times for large and non-trivial ADT transformations. This optimization, together with the user guidance in the form of reusable templates, allows our system to attack problems that are out of scope for existing synthesizers.

We implemented these ideas in a tool called SyntRec, which is built on top of the open source Sketch synthesis platform [19]. Our tool supports expressive correctness specifications that can use arbitrary functions to constrain the behavior of ADT transformations. Like other expressive synthesizers, such as Sketch [18] and Rosette [20, 21], our system relies on exhaustive bounded checking to establish whether a program candidate matches the specification. While this does not provide correctness guarantees beyond a bounded set of inputs, it works well in practice and allows us to tackle complex problems, for which full correctness is undecidable and is beyond the state of the art in automatic verification. For example, our benchmarks include desugaring functions from an abstract syntax tree (AST) into a simpler AST, where correctness is defined in terms of interpreters for the two ASTs. As a result, our synthesizer is able to discover Church encodings for pairs and booleans, given nothing but an interpreter for the lambda calculus. In another benchmark, we show that the system is powerful enough to synthesize a type constraint generator for a simple programming language given the semantics of type constraints. Additionally, several of our benchmarks come from transformation passes implemented in our own compiler and synthesizer.

2 Overview

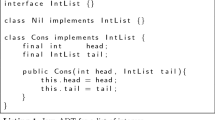
In this section, we use the problem of desugaring a simple language to illustrate the main features of SyntRec. Specifically, the goal is to synthesize a function , which translates an expression in source AST into a semantically equivalent expression in destination AST. Data type definitions for the two ASTs are shown in Fig. 1: the type has five variants (two of which are recursive), while has only three. In particular, the source language construct , which denotes , has to be desugared into a conjunction of two inequalities. Like case classes in Scala, data type variants in SyntRec have named fields.

Fig. 1.

ADTs for two small expression languages

Specification. The first piece of user input required by the synthesizer is the specification of the program’s intended behavior. In the case of , we would like to specify that the desugared AST is semantically equivalent to the original AST, which can be expressed in SyntRec using the following constraint:

This constraint states that interpreting an arbitrary source-language expression (bounded to some depth) must be equivalent to desugaring and interpreting the resulting expression in the destination language. Here, and are regular functions written in SyntRec and defined recursively over the structure of the respective ASTs in a straightforward manner. As we explain in Sect. 3.4, our synthesizer contains a novel optimization called inductive decomposition that can take advantage of the structure of the above specification to significantly improve the scalability of the synthesis process.

Templates. The second piece of user input required by our system is a syntactic template, which describes the space of possible implementations. The template is intended to specify the high-level structure of the program, leaving low-level details for the system to figure out. In that respect, SyntRec follows the SyGuS paradigm [2]; however, template languages used in existing SyGuS tools, such as Sketch or Rosette, work poorly in the context of recursive ADT transformations.

For example, Fig. 2 shows a template for written in Sketch, the predecessor of SyntRec. It is useful to understand this template as we will show, later, how the new language features in SyntRec allow us to write the same template in a concise and reusable manner. This template uses three kinds of synthesis constructs already existing in Sketch: a choice () must be replaced with one of the expressions $e_1,\ldots ,e_n$; a hole must be replaced with an integer or a boolean constant; finally, a generator (such as ) can be thought of as a macro, which is inlined on use, allowing the synthesizer to make different choices for every invocation¹. The task of the synthesizer is to fill in every choice and hole in such a way that the resulting program satisfies the specification.

The template in Fig. 2 expresses the intuition that should recursively traverse its input, , replacing each node with some subtree from the destination language. These destination subtrees are created by calling the recursive, higher-order generator (for “recursive constructor”). constructs a nondeterministically chosen variant of , whose fields, depending on their type, are obtained either by recursively invoking , by invoking (which is itself a generator), or by picking an integer or boolean constant. For example, one possible instantiation of the template ² can lead to . Note that the template for provides no insight on how to actually encode each node of in terms of , which is left for the synthesizer to figure out. Despite containing so little information, the template is very verbose: in fact, more verbose than the full implementation! More importantly, this template cannot be reused for other synthesis problems, since it is specific to the variants and fields of the two data types. Expressing such a template in Rosette will be similarly verbose.

Fig. 2.

Template for in Sketch

Reusable Templates. SyntRec addresses this problem by extending the template language with polymorphic synthesis constructs (PSCs), which essentially support parametrizing templates by the structure of data types they manipulate. As a result, in SyntRec the end user can express the template for with a single line of code:

Here, is a reusable generator defined in a library; its code is shown in Fig. 3. When the user invokes , the body of the generator is specialized to the surrounding context, resulting in a template very similar to the one in Fig. 2. Unlike the template in Fig. 2, however, is not specific to and , and can be reused with no modifications to synthesize desugaring functions for other languages, and even more general recursive ADT transformations. Crucially, even though the reusable template is much more concise than the Sketch template, it does not increase the size of the search space that the synthesizer has to consider, since all the additional choices are resolved during type inference. Figure 3 also shows a compacted version of the solution for , which SyntRec synthesizes in about 8s. The rest of the section gives an overview of the PSCs used in Fig. 3.

Fig. 3.

Left: generic template for Right: solution to the running example

Polymorphic Synthesis Constructs. Just like a regular synthesis construct, a PSC represents a set of potential programs, but the exact set depends on the context and is determined by the types of the arguments to a PSC and its expected return type. SyntRec introduces four kinds of PSCs.

• 1. A Polymorphic Generator is a polymorphic version of a Sketch generator. For example, is a polymorphic generator, parametrized by types and . When the user invokes , and are instantiated with and , respectively.

• 2. Flexible Pattern Matching () expands into pattern matching code specialized for the type of x. In our example, once in is instantiated with , the construct in Line 4 expands into five cases () with the body of duplicated inside each of these cases.

• 3. Field List () expands into an array of all fields of type in a particular variant of , where $\tau$ is derived from the context. Going back to Fig. 3, Line 5 inside maps a function over a field list ; in our example, is instantiated with , which takes an input of type . Hence, SyntRec determines that in this case denotes all fields of type . Note that this construct is expanded differently in each of the five cases that resulted from the expansion of . For example, inside , this construct expands into an empty array ( has no fields of type ), while inside , it expands into the array .

• 4. Unknown Constructor () expands into a constructor for some variant of type $\tau$, where $\tau$ is derived from the context, and uses the expressions $e_1, \ldots , e_n$ as the fields. In our example, the auxiliary generator uses an unknown constructor in Line 11. When is invoked in a context that expects an expression of type , this unknown constructor expands into . If instead is expected to return an expression of type , then the unknown constructor expands into . If the expected type is an integer or a boolean, this construct expands into a regular Sketch hole .

Even though the language provides only four PSCs, they can be combined in novel ways to create richer polymorphic constructs that can be used as library components. The generators and in Fig. 3 are two such components.

Fig. 4.

Kernel language

The component expands into an arbitrary field of type $\tau$, where $\tau$ is derived from the context. Its implementation uses the field list PSC to obtain the array of all fields of type $\tau$, and then accesses a random element in this array using an integer hole. For example, if is used in a context where the type of is and the expected type is , then expands into which is semantically equivalent to .

The component is a polymorphic version of the recursive constructor for in Fig. 2, and can produce ADT trees of any type up to a certain depth. Note that since is a polymorphic generator, each call to in the argument to the unknown constructor (Line 11) is specialized based on the type required by that constructor and can make different non-deterministic choices. Similarly, it is possible to create other generic constructs such as iterators over arbitrary data structures. Components such as these are expected to be provided by expert users, while end users treat them in the same way as the built-in PSCs. The next section gives a formal account of the SyntRec’s language and the synthesis approach.

3 SyntRec Formally

3.1 Language

Figure 4 shows a simple kernel language that captures the relevant features of SyntRec. In this language, a program consists of a set of ADT declarations followed by a set of function declarations. The language distinguishes between a standard function $\overline{f}$, a generator $\hat{f}$ and a polymorphic generator $\hat{\hat{f}}$. Functions can be passed as parameters to other functions, but they are not entirely first-class citizens because they cannot be assigned to variables or returned from functions. Function parameters lack type annotations and are declared as type fun, but their types can be deduced from inference. Similarly, expressions are divided into standard expressions that does not contain any unknown choices ($\overline{e}$), existing synthesis constructs in Sketch ($\hat{e}$), and the new PSCs ($\hat{\hat{e}}$). The language also has support for arrays with expressions for array creation ($\{e_1, e_2, ..., e_n\}$) and array access ($e_1[e_2]$). An array type is represented as $\theta [~]$. In this formalism, we use the Greek letter $\tau$ to refer to a fully concrete type and $\theta$ to refer to a type that may involve type variables. The distinction between the two is important because PSCs can only be expanded when the types of their context are known. We formalize ADTs as tagged unions $\tau = \sum variant_i$, where each of the variants is a record type $variant_i = name_{i}\left\{ l_{k}^{i}:\tau _{k}^{i}\right\} _{k<n_i}$. Note that ADTs in SyntRec are not polymorphic. The notation $\{a_i\}_i$ is used to denote the $\{a_1, a_2,...\}$.

3.2 Synthesis Approach

Given a user-written program $\hat{\hat{P}}$ that can potentially contain PSCs, choices and holes, and a specification, the synthesis problem is to find a program $\overline{P}$ in the language that only contains standard expressions ($\overline{e}$) and functions ($\overline{f}$). SyntRec solves this problem using a two step approach as shown below:

First, SyntRec uses a set of expansion rules that uses bi-directional type checking to eliminate the PSCs. The result is a program that only contains choices and holes. The second step is to use a constraint-based approach to solve for these choices. The next subsections will present each of these steps in more detail.

3.3 Type-Directed Expansion Rules

We will now formalize the process of specializing and expanding the PSCs into sets of possible expressions. We should first note that the expansion and the specialization of the different PSCs interact in complex ways. For example, for the construct in the running example, the system cannot determine which cases to generate until it knows the type of , which is only fixed once the polymorphic generator for is specialized to the calling context. On the other hand, if a polymorphic generator is invoked inside the body of a (like in the running example), we may not know the types of the arguments until after the is expanded into separate cases. Because of this, type inference and expansion of the PSCs must happen in tandem.

We formalize the process of expanding PSCs using two different kinds of judgements. The typing judgement $\varGamma \vdash e:\theta$ determines the type of an expression by propagating information bottom-up from sub-expressions to larger expressions. On the other hand, PSCs cannot be type-checked in a bottom-up manner; instead, their types must be inferred from the context. The expansion judgment $\varGamma \vdash e~\xrightarrow {\theta }~e'$ expands an expression e involving PSCs into an expression $e'$ that does not contain PSCs (but can contain choices and holes). In this judgment, $\theta$ is used to propagate information top-down and represents the type required in a given context; in other words, after this expansion, the typing judgement $\varGamma \vdash e' : \theta$ must hold. We are not the first to note that bi-directional typing [15] can be very useful in pruning the search space for synthesis [13, 16], but we are the first to apply this in the context of constraint-based synthesis and in a language with user-provided definitions of program spaces.

Fig. 5.

Expansion rules for various language constructs

The expansion rules for functions and PSCs are shown in Fig. 5. At the top level, given a program P, every function in P is transformed using the expansion rule FUN. The body of the function is expanded under the known output type of the function. The most interesting cases in the definition of the expansion judgment correspond to the PSCs as outlined below. The expansion rules for the other expressions are straightforward and are elided for brevity.

Field List. The rule FL shows how a field list is expanded. If the required type is an array of $\tau _0$, then this PSC can be expanded into an array of all fields of type $\tau _0$.

Flexible Pattern Matching. For each case, the body of is expanded while setting x to a different type corresponding to each variant $name_{i}\left\{ l_{k}^{i}:\tau _{k}^{i}\right\} _{k<n_i}$ as shown in the rule FPM. Here, the argument to is required to be a variable so that it can be used with a different type inside each of the different cases. Note that each case is expanded independently, so the synthesizer can make different choices for each $e_{i}$.

Unknown Constructor. If the required type is an ADT, the rule UC1 expands the expressions passed to the unknown constructor based on the type of each field of each variant of the ADT and uses the resulting expressions to initialize the fields in the relevant constructor. It returns a expression with all these constructors as the arguments. If the required type is a primitive type (int or bit), the unknown constructor is expanded into a Sketch hole by the rule UC2.

Polymorphic Generator Calls. When the expansion encounters a call to a polymorphic generator, the generator will be expanded and specialized according to the PG rule. When a generator is called with arguments $\{e_{i}\}_i$, we can separate the arguments into expressions that can be typed using the standard typing judgement, and expressions such as that cannot. In the rule, we assume, without loss of generality, that the first k expressions can be typed and the reminder cannot. The basic idea behind the expansion is as follows. First, the rule obtains the types of the first k arguments and unifies them with the types of the formal parameters of the function to get a type substitution S. The arguments to the original call are expanded with our improved knowledge of the types, and the body of the generator is then inlined and expanded in turn. The actual implementation also keeps track of how many times each generator has been inlined and replaces the generator invocation with when the inlining bound has been reached.

The above expansion rules fail if a type variable is encountered in places where a concrete type is expected, and in such cases the system will throw an error. For example, expressions such as , where is as defined in Fig. 3, cannot by type-checked in our system because the expected type of the inner call cannot be determined using top-down type propagation.

3.4 Constraint-Based Synthesis

Once we have a program with a fixed number of integer unknowns, the synthesis problem can be encoded as a constraint $\exists \phi .~\forall \sigma .~P(\phi , \sigma )$ where $\phi$ is a control vector describing the set of choices that the synthesizer has to make, $\sigma$ is the input state of the program, and $P(\phi , \sigma )$ is a predicate that is true if the program satisfies its specification under input $\sigma$ and control $\phi$. Our system follows the standard approach of unrolling loops and inlining recursive calls to derive P and uses counterexample guided inductive synthesis (CEGIS) to solve this doubly quantified problem [18]. For readers unfamiliar with this approach, the most relevant aspect from the point of view of this paper is that the doubly quantified problem is reduced to a sequence of inductive synthesis steps. At each step, the system generates a solution that works for a small set of inputs, and then checks if this solution is in fact correct for all inputs; otherwise, it generates a counter-example for the next inductive synthesis step.

Applying the standard approach can, however, be problematic in our context especially with regards to inlining recursive calls. For instance, consider the example from Sect. 2. Here, the function that has to be synthesized is a recursive function. If we were to inline all the recursive calls to , then a given concrete value for the input $\sigma$ such as , will exercise multiple cases within ( for the example). This is problematic in the context of CEGIS, because at each inductive synthesis step the synthesizer has to jointly solve for all these variants of which greatly hinders scalability when the source language has many variants.

3.5 Inductive Decomposition

The goal of this section is to leverage the inductive specification to potentially avoid inlining the recursive calls to the synthesized function. This idea of treating the specification as an inductive hypothesis is well known in the deductive verification community where the goal is to solve the following problem: $\forall \sigma .\ P(\phi _0, \sigma )$. However, in our case, we want to apply this idea during the inductive synthesis step of CEGIS where the goal is to solve $\exists \phi .\ P(\phi , \sigma _0)$ which has not been explored before.

Definition 1

(Inductive Decomposition). Suppose the specification is of the form $interp_s(e) = interp_d(trans(e))$ where trans is the function that needs to be synthesized. Let $trans(e')$ be a recursive call within trans(e) where $e'$ is strictly smaller term than e. Inductive Decomposition is defined as the following substitution: 1. Replace $trans(e')$ with a special expression $\boxed {e'}$. 2. When inlining function calls, apply the following rules for the evaluation of $\boxed {e'}$:

i.e. Inductive Decomposition works by delaying the evaluation of a recursive $trans(e')$ call by replacing it with a placeholder that tracks the input $e'$. Then, if the algorithm encounters these placeholders when inlining $interp_d$ in the specification, it replaces them directly with $interp_s(e')$ which we know how to evaluate, thus, eliminating the need to inline the unknown trans function. This replacement is sound because the specification states $interp_d(trans(e')) = interp_s(e')$. If the algorithm encounters the placeholders in any other context where the inductive specification can not be leveraged, it defaults to evaluating $trans(e')$.

Theorem 1

Inductive Decomposition is sound and complete. In other words, if the specification is valid before the substitution, then it will be valid after the substitution and vice-versa.

A proof of this theorem can be found in the tech report [6]. Although the Inductive Decomposition algorithm imposes restrictions on which recursive calls can be eliminated, it turns out that for many of the ADT transformation scenarios, the algorithm can totally eliminate all recursive calls to trans. For instance, in the running example, because of the inductive structure of , all placeholders for recursive calls will occur only in the context of which can be replaced by according to the algorithm. Thus, after the substitution, the function is no longer recursive and moreover, the desugaring for the different variants can be synthesized separately. For the running example, we gain a 20X speedup using this optimization. Our system also implements several generalizations of the aforementioned optimization that are detailed in the tech report [6].

4 Evaluation

Benchmarks. We evaluated our approach on 23 benchmarks as shown in Fig. 6. All benchmarks along with the synthesized solutions can be found in the tech report [6]. Since there is no standard benchmark suite for morphism problems, we chose our benchmarks from common assignment problems (the lambda calculus ones), desugaring passes from Sketch compiler and some standard data structure manipulations on trees and lists. The AST optimization benchmarks are from a system that synthesizes simplification rules for SMT solvers [17].

Templates. The templates for all our benchmarks use one of the four generic descriptions we have in the library. All benchmarks except and AST optimizations use a generalized version of the generator seen in Fig. 3 (the exact generator is in the tech report). This generator is also used as a template for problems that are very different from the desugaring benchmarks such as the list and the tree manipulation problems, illustrating how generic and reusable the templates can be. The benchmark differs slightly from the others as its ADT definitions have arrays of recursive fields and hence, we have a version of the recursive replacer that also recursively iterates over these arrays. The benchmark requires a template that has nested pattern matching. Another interesting example of reusability of templates is the AST optimization benchmarks. All 5 benchmarks in this category are synthesized from a single library function. The column in Fig. 6 shows the number of lines used in the template for each benchmark. Most benchmarks have a single line that calls the appropriate library description similar to the example in Sect. 2. Some benchmarks also specify additional components such as helper functions that are required for the transformation. Note that these additional components will also be required for other systems such as Leon and Synquid.

4.1 Experiments

Methodology. All experiments were run on a machine with forty 2.4 GHz Intel Xeon processors and 96 GB RAM. We ran each experiment 10 times and report the median.

Hypothesis 1: Synthesis of Complex Routines is Possible. Figure 6 shows the running times for all our benchmarks ( column). SyntRec can synthesize all but one benchmark very efficiently when run on a single core using less than 1 GB memory—19 out of 23 benchmarks take $\le$1 min. Many of these benchmarks are beyond what can be synthesized by other tools like Leon, Rosette, and others and yet, SyntRec can synthesize them just from very general templates. For instance, the benchmarks are automatically discovering the Church encodings for boolean operations and pairs, respectively. The benchmark synthesizes an algorithm to produce type constraints for lambda calculus ASTs to be used to do type inference. The output of this algorithm is a conjunction of type equality constraints which is produced by traversing the AST. Several other desugaring benchmarks have specifications that involve complicated interpreters that keep track of state, for example. Some of these specifications are even undecidable and yet, SyntRec can synthesize these benchmarks (up to bounded correctness guarantees). The figure also shows the size of the synthesized solution ( column)³.

There is one benchmark () that cannot be solved by SyntRec using a single core. Even in this case, SyntRec can synthesize the desugaring for 6 out of 7 variants in less than a minute. The unresolved variant requires generating expression terms that are very deep which exponentially increases the search space. Luckily, our solver is able to leverage multiple cores using the random concretization technique [7] to search the space of possible programs in parallel. The column in Fig. 6 shows the running times for all benchmarks when run on 16 cores. SyntRec can now synthesize all variants of the benchmark in about 9 min.

The results discussed so far are obtained for optimal search parameters for each of the benchmarks. We also run an experiment to randomly search for these parameters using the parallel search technique with 16 cores and report the results in the column. Although these times are higher than when using the optimal parameters for each benchmark ( column), the difference is not huge for most benchmarks.

Fig. 6.

Benchmarks. All reported times are in seconds. $\bot$ stands for timeout (>45 min) and N/A stands for not applicable.

Hypothesis 2: The Inductive Decomposition Improves the Scalability. In this experiment, we run each benchmark with the Inductive Decomposition optimization disabled and the results are shown in Fig. 6 ( column). This experiment is run on a single core. First of all, the technique is not applicable for the AST optimization benchmarks because the functions to be synthesized are not recursive. Second, for three benchmarks—the $\lambda$-calculus ones and the benchmark, we noticed that their specifications do not have the inductive structure and hence, the optimization never gets triggered.

But for the other benchmarks, it can be seen that inductive decomposition leads to a substantial speed-up on the bigger benchmarks. Three benchmarks time out (>45 min) and we found that times out even when run in parallel. In addition, without the optimization, all the different variants need to be synthesized together and hence, it is not possible to get partial solutions. The other benchmarks show an average speedup of 2X with two benchmarks having a speedup >10X. We found that for benchmarks that have very few variants, such as the list and the tree benchmarks, both versions perform almost similarly.

To evaluate how the performance depends on the number of variants in the initial AST, we considered the benchmark that synthesizes a desugaring for a source language with 15 variants into a destination language with just 4 variants. We started the benchmark with 3 variants in the source language while incrementally adding the additional variants and measured the run times both with the optimization enabled and disabled. The graph of run time against the number of variants is shown in Fig. 7. It can be seen that without the optimization the performance degrades very quickly and moreover, the unoptimized version times out (>45 min) when the number of variants is >11.

4.2 Comparison to Other Tools

We compared SyntRec against three tools—Leon, Synquid and Rosette that can express our benchmarks. The list and the tree benchmarks are the typical benchmarks that Leon and Synquid can solve and they are faster than us on these benchmarks. However, this difference is mostly due to SyntRec’s final verification time. For these benchmarks, our verification is not at the state of the art because we use a very naive library for the related functions used in their specifications. We also found that Leon and Synquid can synthesize some of our easy desugaring benchmarks that requires constructing relatively small ADTs like and in almost the same time as us. However, Leon and Synquid were not able to solve the harder desugaring problems including the running example. We should also note that this comparison is not totally apples-to-apples as Leon and Synquid are more automated than SyntRec.

Fig. 7.

Run time (in seconds) versus the number of variants of the source language for the benchmark with and without the optimization.

For comparison against Rosette, we should first note that since Rosette is also a SyGus solver, we had to write very verbose templates for each benchmark. But even then, we found that Rosette cannot get past the compilation stage because the solver gets bogged down by the large number of recursive calls requiring expansion. For the other smaller benchmarks that were able to get to the synthesis stage, we found that Rosette is either comparable or slower than SyntRec. For example, the benchmark takes about 2 min in Rosette compared to 2 s in SyntRec. We attribute these differences to the different solver level choices made by Rosette and Sketch (which we used to built SyntRec upon).

5 Related Work

There are many recent systems that synthesize recursive functions on algebraic data-types. Leon [3, 8, 9] and Synquid [16] are two systems that are very close to ours. Leon, developed by the LARA group at EPFL, is built on prior work on complete functional synthesis by the same group [10] and moreover, their recent work on Synthesis Modulo Recursive Functions [8] demonstrated a sound technique to synthesize provably correct recursive functions involving algebraic data types. Unlike our system, which relies on bounded checking to establish the correctness of candidates, their procedure is capable of synthesizing provably correct implementations. The tradeoff is the scalability of the system; Leon supports using arbitrary recursive predicates in the specification, but in practice it is limited by what is feasible to prove automatically. Verifying something like equivalence of lambda interpreters fully automatically is prohibitively expensive, which puts some of our benchmarks beyond the scope of their system. Synquid [16], on the other hand, uses refinement types as a form of specification to efficiently synthesize programs. Like our system, Synquid also depends on bi-directional type checking to effectively prune the search space. But like Leon, it is also limited to decidable specifications. There has also been a lot of recent work on programming by example systems for synthesizing recursive programs [1, 4, 13, 14]. All of these systems rely on explicit search with some systems like [13] using bi-directional typing to prune the search space and other systems like [1] using specialized data-structures to efficiently represent the space of implementations. However, they are limited to programming-by-example settings, and cannot handle our benchmarks, especially the desugaring ones.

Our work builds on a lot of previous work on SAT/SMT based synthesis from templates. Our implementation itself is built on top of the open source Sketch synthesis system [18]. However, several other solver-based synthesizers have been reported in the literature, such as Brahma [5]. More recently, the work on the solver aided language Rosette [20, 21] has shown how to embed synthesis capabilities in a rich dynamic language and then how to leverage these features to produce synthesis-enabled embedded DSLs in the language. Rosette is a very expressive language and in principle can express all the benchmarks in our paper. However, Rosette is a dynamic language and lacks static type information, so in order to get the benefits of the high-level synthesis constructs presented in this paper, it would be necessary to re-implement all the machinery in this paper as an embedded DSL.

There is also some related work in the context of using polymorphism to enable re-usability in programming. [11] is one such approach where the authors describe a design pattern in Haskell that allows programmers to express the boilerplate code required for traversing recursive data structures in a reusable manner. This paper, on the other hand, focuses on supporting reusable templates in the context of synthesis which has not been explored before. Finally, the work on hole driven development [12] is also related in the way it uses types to gain information about the structure of the missing code. The key difference is that existing systems like Agda lack the kind of symbolic search capabilities present in our system, which allow it to search among the exponentially large set of expressions with the right structure for one that satisfies a deep semantic property like equivalence with respect to an interpreter.

6 Conclusion

The paper has shown that by combining type information from algebraic data-types together with the novel Inductive Decomposition optimization, it is possible to efficiently synthesize complex functions based on pattern matching from very general templates, including desugaring functions for lambda calculus that implement non-trivial Church encodings.