Drug Resistance in Infectious Diseases: Modeling, Parameter Estimation and Numerical Simulation

Abstract

Infectious diseases are drawing our attention again. In recent years, we have been confronted with SARS, bird-flu, swine-flu and many other severe diseases. In addition, pathogens are getting resistant to drugs controlling them. In this paper we establish a new population dynamical system of infectious diseases including drug treatment. We take into account both sensitive and resistant parasites. The unknown model parameters are fitted based on a set of data for malaria from Cisse, Burkina Faso. The fitted model is used to investigate the influence of drug treatment on drug resistance. Based on these investigations, treatment strategies to reduce drug resistance can be elaborated.

1 Introduction

This paper is organized as follows. In the first section we give a short overview on the drug resistance models existing so far. In Section 2, we present a new model describing the dynamics of pathogen, transmitter and human populations including drug treatment. Section 3 is devoted to doing parameter estimation and simulation. Estimation results and simulations with controllable factors are performed here. The last section is reserved for discussion of the simulation results and conclusions.

As we know, infectious diseases were and are still being a big burden to every country. For a long time a lot of scientists have been studying them intensively [1, 8, 12]. Although being considered as classical field of mathematical modeling, it is now attracting a lot of attention again. Pathogens are getting more resistant to drugs, infectious diseases can spread very fast and become a danger for the populations. Including this effect in the model equations is an important condition to meet reality in epidemics.

We are going to set up a mathematical model under general aspects, but we select malaria as the central case, where we have a chance to obtain data to calibrate and validate our model.

For the rest of this section, we mainly discuss modeling of drug resistance with central focus on malaria. Historically, there has been a lot of research on this disease, see [5, 7, 13] and references therein. However, up to now it is very difficult to obtain satisfactory malaria models. In general, before modeling authors have their own questions. They would then call a new model to be “good enough” if it is able to answer their questions. One of the challenges with malaria is that it comes together with Anopheles mosquitoes and parasites—Plasmodium falciparum, Plasmodium vivax, Plasmodium ovale and Plasmodium malariae. Their organisms are much more complex compared to other pathogens with single-cell or even simpler- such as bacteria, archaea, viruses, etc. This can also partly explain why there are only few mathematical models concerning drug treatment in malaria.

What may influence drug resistance?

• – In most diseases, it takes long time to find out which factors may characterize and reduce drug efficiency. Usually, there are many individuals of the pathogen population which already have “resistant” mechanisms. They are naturally not eliminated by drugs. When infected people take medicine, it reduces sensitive parasites and makes good environment for resistance growth.

• – In malaria, parasite organisms are very complex, they would either mutate or adapt variously. They have a better chance to survive after natural selection and maintain their best genetic system. Hence, their new generations are more “fit” in a drug environment.

• – Another important reason for drug resistance is that malaria is more widespread in tropical countries, like in Africa, where it is difficult to have a global policy to treat all patients in a proper way.

For the rest of this paper, we are more interested in mathematical malaria modeling. In history, there were many valuable contributions by Ross, MacDonald, May, Dietz, see [1, 5] and references therein. However, resistance was not well investigated. Mathematicians have only recently started to pay attention to this field. Two recent malaria models concerning drug resistance came from Aneke [2] and Esteva et al. [6]. Here the authors described a model of hosts and vectors dealing with both resistant and sensitive strains. In these papers and also some other cases, authors focus on analyzing the models to establish positive equilibrium and studying their stability under certain assumptions. Although in [6] the authors tried numerical simulation, they said that the model needed to be validated using realistic epidemiological data. So far there was very few data available to calibrate malaria and other vector-borne disease models.

In this paper, we derive a model which consists of differential equations including all host and pathogen populations. Such models are complex to perform analysis, and thus we are going to study them numerically. Since from experiments not all parameters are known directly, we have to use parameter estimation techniques to determine their values. After this, the model is used for computer experiments. We obtain results on treatment strategies, some of which have been recently confirmed by experimentalists after a lot of works in hospitals and laboratories [7, 13].

2 Modeling of Population Dynamics Including Drug Treatment

We divide this part into two sub-sections: the first one introduces all model compartments and their network, the second one presents model formulation.

2.1 The Network of Compartments

There are two main groups of infectious diseases: the first group (such as HIV/AIDS, tuberculosis) can be transmitted directly from one person to another and the second group (such as malaria, dengue hemorrhagic fever) is transmitted only via an intermediate host. From the perspective of infectious diseases, vectors are the transmitters of disease-causing organisms that carry the pathogens from one host to another [14]. That’s why a disease belonging to the second group is called a vector-borne disease.

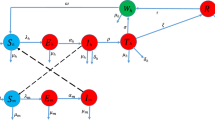
As we discussed before, we would like to model dynamics of pathogen, vector and human populations. We consider two hosts: number of humans denoted by H ₁ and vectors denoted by H ₂. The pathogens within human hosts are denoted by P. Like in the classical case, there are three compartments for human hosts which we call susceptible H _1s , infected H _1i , recovered H _1r . We have two compartments for vector hosts H _2s , H _2i —susceptible and infected. Since drugs are employed, there are two compartments for pathogens, non-resistant and resistant P _n , P _r , respectively. All transmissions among the seven groups are described in Fig. 1.

Fig. 1

Network for the population dynamics with drug treatment

2.2 Model Formulation

Now we give an overview of the modeled processes, as schematically indicated in Fig. 1. Since our focus is drug treatment for humans, so the model may not include some interference applying on vectors directly. We include the influence of drugs on the host population and the subsequent effects on pathogen population.

Remark.

During the course of our study, we discover that some parts of the extracted data are not precise enough and can have some effect on parameter estimation and simulation. We revise them and exclude the imprecise values. The model is improved in parallel with this process. Despite the fact that the usable data is less, we can obtain better fit compared to the first estimation, see Fig. 3.

2.2.1 Susceptible Human Population H _1s

In vector-borne diseases, human hosts become infected only after coming in contact with vectors, so there is often no vertical transmission, e.g. from parents to children. Every new offspring goes to the susceptible class. Like other epidemic models, we use common denotations for the natural birth rates of susceptible, infected, recovered human classes $b_{1s},b_{1i},b_{1r}$. Also as convention, mortality rate of H _1s is denoted by m _1s , infection rate by i ₁ and re-susceptibility rate by r (individuals from recovered class H _1r after a certain time come back to susceptible class H _1s ). Values of $m_{1s},i_{1}$ are given in the next section and r is an unknown parameter which can be found after fitting the data. The dynamic equation of the susceptible human population is the following:

$$\frac{dH_{1s}} {dt} = b_{1s}H_{1s} + b_{1i}H_{1i} + b_{1r}H_{1r} - i_{1} \frac{H_{2i}} {H_{2i} + H_{2s}}H_{1s} + rH_{1r} - m_{1s}H_{1s}.$$

(1)

Notice that the infection term depends on $\frac{H_{2i}} {H_{2i}+H_{2s}}$, which implies that there are too many vectors so that they have to compete with each other to get successful contact to humans (e.g., obtain a blood meal in case of malaria). This is a quite usual situation in Africa, where the tropical climate is suitable for vector (mosquito) development. Although mainly infected female Anopheles mosquitoes can transmit malaria, they still have to compete with other un-infected mosquitoes to get blood meals. On the other hand, the size of the mosquito population induces a corresponding protection force from human side.

Fig. 3

The observed (points) and predicted (dashed curves) populations. Data from middle of January to November 2004, [11]. All together we use 427 measurement data. These data points are plotted together with their error bars (20% of each peak measurements). Time unit is 5 days

Concerning additional details for parameter r, we are aware that different drugs have different half-lives. They partly remain inside human bodies after treatment and provide the same protection as immunity. Medically, we consider five times of drug half-life equal to wash-out time. When drug is washed out and immunity is no longer active, the person returns to the susceptible class. This process is modeled by formula $r = k_{r}r_{0}$, where $r_{0} = {[\text{max}(T,d)]}^{-1}$, T is natural immune duration, d is drug wash-out duration; k _r is a scalar factor subject to estimation. After fitting, we use this formula for control simulation, with the controllable parameter d.

2.2.2 Infected Human Population H _1i

After susceptible individuals get infected with rate i ₁, they go to the infected class. Here are two possibilities how they can move out of this class: either they recover after treatment or they can not recover and die. The natural and disease-induced mortality rate is denoted by m _1i with value based on literature [11], and the recovery rate μ is unknown parameter.

$$\frac{dH_{1i}} {dt} = i_{1} \frac{H_{2i}} {H_{2i} + H_{2s}}H_{1s} - \mu H_{1i} - m_{1i}H_{1i}.$$

(2)

Moreover, we foresee that the recovery rate μ depends on the individual immunity, the employed medical treatment and the way how the drug is administrated. We are going to take the data from Cisse in Burkina Faso, a small and poor village. We should notice that most of the local population does not have access to any treatment easily. With support from a project between Heidelberg researchers and local people, classical Chloroquine regimen was given to all patients and showed good effect. That is why in simulation we can assume that drugs start with a good efficacy. When one patient takes the full dose as recommended, all his/her sensitive pathogens are killed at rate e. The proportion of people that follows proper treatment is expressed by α.

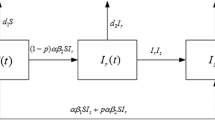
In general, most of the patients carry both sensitive and resistant parasites. Drug treatment strengthens the immunity and shortens the recovery process. In other words, it helps to increase the recovery rate. We combine immune and treatment effects in formula

$$\mu = k_{\beta }e\beta \alpha + \beta (1 - \alpha ),$$

where β is the rate of parasites which are eliminated by natural host immunity without treatment, k _β e is the factor which expresses how drugs strengthen the immunity in treated patients. The value of k _β is subject to estimation.

2.2.3 Recovered Human Population H _1r

All recovered individuals from H _1i go to the recovered class H _1r . For a certain while they have protection due to the retained drug and natural immunity. Depending on different diseases they can or can not be reinfected again. With malaria, especially in highly endemic areas, all recovered individuals eventually lose their immunity and return to susceptible class. The process can be fast or slow depending on drug wash-out duration and individual health. We have already explained the meaning of r in the Sect. 2.2.1 above. We also call m _1r mortality rate of recovered class H _1r , the value of m _1r is given in Table 1.

$$\frac{dH_{1r}} {dt} = \mu H_{1i} - rH_{1r} - m_{1r}H_{1r}.$$

(3)

Table 1 All known parameters

2.2.4 Susceptible Vector Population H _2s

This compartment is similar to the susceptible human compartment. However, since parasites do not influence vectors in the same way as they influence humans, there is no recovery or re-susceptibility effect.

Let $b_{2s},b_{2i}$ be the unknown birth-rates of susceptible and infected vectors. In addition, eggs from vectors (mosquitoes) are supposed to be able to hibernate over unfavorable time spans and hatch to become new vectors when the season provides better conditions. This process has an effect close to immigration and emigration, modeled by parameter b ₂. Vectors become infected on contacting infected humans in class H _1i , this is modeled by rate i ₂. All of these four parameters are subject to estimation. Mortality rate of vectors m _2s is taken as in [11].

$$\frac{dH_{2s}} {dt} = b_{2s}H_{2s} + b_{2i}H_{2i} + b_{2} - i_{2}\left ( \frac{H_{1i}} {H_{1s} + H_{1i} + H_{1r}}\right )H_{2s} - m_{2s}H_{2s}.$$

(4)

2.2.5 Infected Vector Population H _2i

Expectedly, the infected vector population and the infected human population have similar dynamics. All infected individuals from susceptible class H _2s go to H _2i . Since the life-cycle of vectors is not so long, in most cases parasites stay in vectors’ abdomen until they die. The mortality rate of vectors is denoted by m _2i , its value is given in Table 1.

$$\frac{dH_{2i}} {dt} = i_{2}\left ( \frac{H_{1i}} {H_{1s} + H_{1i} + H_{1r}}\right )H_{2s} - m_{2i}H_{2i}.$$

(5)

2.2.6 Non-resistant Parasite Population P _n

Now we pay attention to parasite population in humans. They are supposed to be inside the infected human class H _1i , so naturally depend on H _1i . Since this dependence is likely reduced when the number of infected human becomes large, we use Michaelis–Menten relation, involving $\frac{H_{1i}} {C+H_{1i}}$. We also assume that parasite population growth follows the logistic rule governed by rate $b_{pn},b_{pr}$ and a maximal capacity K.

Unlike the hosts, parasites usually clone themselves, so in some sense there is no “death.” It practically applies for malaria parasites in humans, they only multiply asexually inside human red blood cells. On the other hand, all parasites inside infected hosts also die out due to the mortality of the infected hosts.

For a given treatment, there is the proportion α of the infected human population H _1i , who received full doses. Immunity and drug can eliminate pathogens with rate (μ + α e), e presents the rate at which (sensitive) parasites are eliminated by drug.

Also due to drug presence, some sensitive pathogens need to change themselves to be able to increase their chances of survival, such as by mutation or adaptation. This makes a certain ratio of sensitive pathogens become resistant, the process is occurring with rate

$$s = s_{0} + k_{d}\frac{\alpha \text{min}(d,d_{0})} {e}.$$

The rate s ₀ describes the mutation and the part $k_{d}\alpha \min (d,d_{0})/e$ describes the adaption rate. We assume that the adaption rate is directly increased in the same time with the proportion α of treatment and drug wash-out duration d, but inversely proportional to the efficacy e of the given treatment. There is also a parameter d ₀, an upper threshold of drug wash out duration d, which implies that above a certain limit parasite adaptation rate would not increase considerably but rather stay the same. Factor k _d is an unknown subject to estimation.

$$\frac{dP_{n}} {dt} = b_{pn} \frac{H_{1i}} {C + H_{1i}}\left (1 -\frac{P_{n} + P_{r}} {K} \right )P_{n} - m_{1i}P_{n} - (\mu + \alpha e)P_{n} - sP_{n}.$$

(6)

2.2.7 Resistant Parasite Population P _r

As we mentioned before, the resistant parasite population P _r grows with the rate b _pr . It decreases due to H _1i -death rate m _1i or is eliminated by host immunity μ. Since resistant parasite population is fitter in drug presence, it gains some new ones from sensitive population sP _n .

$$\frac{dP_{r}} {dt} = b_{pr} \frac{H_{1i}} {C + H_{1i}}\left (1 -\frac{P_{n} + P_{r}} {K} \right )P_{r} - m_{1i}P_{r} - \mu P_{r} + sP_{n}.$$

(7)

Now we put together all the equations (1)–(7). We obtain one system which is related to our network in Fig. 1. This shows clearly what is included in the dynamical system:

$$\begin{array}{rcl} \begin{array}{l} \frac{dH_{1s}} {dt} = b_{1s}H_{1s} + b_{1i}H_{1i} + b_{1r}H_{1r} - i_{1} \frac{H_{2i}} {H_{2i}+H_{2s}}H_{1s} + rH_{1r} - m_{1s}H_{1s}, \\ \frac{dH_{1i}} {dt} = i_{1} \frac{H_{2i}} {H_{2i}+H_{2s}}H_{1s} - \mu H_{1i} - m_{1i}H_{1i}, \\ \frac{dH_{1r}} {dt} = \mu H_{1i} - rH_{1r} - m_{1r}H_{1r}, \\ \frac{dH_{2s}} {dt} = b_{2s}H_{2s} + b_{2i}H_{2i} + b_{2} - i_{2} \frac{H_{1i}} {H_{1s}+H_{1i}+H_{1r}}H_{2s} - m_{2s}H_{2s}, \\ \frac{dH_{2i}} {dt} = i_{2} \frac{H_{1i}} {H_{1s}+H_{1i}+H_{1r}}H_{2s} - m_{2i}H_{2i}, \\ \frac{dP_{n}} {dt} = b_{pn} \frac{H_{1i}} {C+H_{1i}}\left (1 -\frac{P_{n}+P_{r}} {K} \right )P_{n} - m_{1i}P_{n} - (\mu + \alpha e)P_{n} - sP_{n}, \\ \frac{dP_{r}} {dt} = b_{pr} \frac{H_{1i}} {C+H_{1i}}\left (1 -\frac{P_{n}+P_{r}} {K} \right )P_{r} - m_{1i}P_{r} - \mu P_{r} + sP_{n}\\ \end{array} & &\end{array}$$

(8)

where

$$r = k_{r}r_{0} = k_{r}{\text{max}}^{-1}(T,d),$$

$$\quad\mu = k_{\beta }e\beta \alpha + \beta (1 - \alpha ),$$

$$s = s_{0} + k_{d}\alpha {e}^{-1}\text{min}(d,d_{ 0}).$$

All initial conditions are given:

$$(H_{1s},H_{1i},H_{1r},H_{2s},H_{2i},P_{n},P_{r})({t}^{0}) = (H_{ 1s}^{0},H_{ 1i}^{0},H_{ 1r}^{0},H_{ 2s}^{0},H_{ 2i}^{0},P_{ n}^{0},P_{ r}^{0}) \geq 0,$$

$$\qquad\qquad\text{especially the susceptible classes }H_{1s}^{0},H_{ 2s}^{0} > 0.$$

This is a non-linear differential equation system. The system is designed for vector-borne diseases. Compared to the already established models concerning drug resistance of vector-borne diseases, such as in [2, 6], we add two new compartments of parasites. They are either sensitive or resistant to the given drug. Drug treatment can take effect on infected human hosts H _1i , sensitive parasites P _n and partly on resistant parasites P _r inside the infected humans.

3 Parameter Estimation and Numerical Simulation

For numerical study, we often use finite interval. For short time periods, parameters related to human hosts do not change very much in general. That is why we are going to specify some factors, in order to reduce the complexity of the problem.

This section contains data extraction, all known and unknown parameters, establish a parameter estimation problem and a simulation problem. Using the software package VPLAN [9], we can solve the two problems. All the results are presented in detail.

3.1 Data Extraction

Concerning observation data, they are mainly extracted from [11], a project which have been done in Burkina Faso. We make the following assumptions:

• – The study focused on children and all observations were generalized for the whole town.

• – In the period of study, most of the clinical malaria cases were treated so most of the infected people recovered after treatment. Whole population was only slightly decreased due to malaria.

• – Given a certain drug, all parasites are either sensitive or resistant.

In addition, we assume that the observation errors are normally distributed and can be approximated by 20% of the peak values of each variable measurement.

3.2 Parameter Values

Before simulation in the case of malaria in Burkina Faso, we have to specify all parameters to meet the specific situation. We present all parameters in two tables: the first one for known parameters and the second for unknown parameters. Our time unit is 5 days.

After several discussions with experts in epidemiology, also based on the data from literature, we take some factors as constants over the year of study (2004): birth rate and mortality rate of human classes, mortality rate of vectors (mosquitoes), etc. We also take into account the properties of the drugs that were given (mainly Chloroquine) and its efficacy. We then obtain a list of the known parameters as given in Table 1. Infection rate i ₁ is a piecewise linear function as in Fig. 2.

Fig. 2

Approximated function of human infection rate i ₁, based on [11] and information about the proportion of infected human class

In Table 2 we present all unknown parameters. We plan to estimate them by piecewise functions, each interval corresponds to 1 month. We state also some constraints needed to analyze estimation results.

Table 2 All unknown parameters for estimation

3.3 Setup of Parameter Estimation Problem and Simulation Problem

In this part, we recall a classical problem concerning parameter estimation in differential equations and specify our problems to be solved later. Interested readers are referred to [3] and references therein for related information.

For the rest of this section, without further notice, all variables are elements of ${\mathbb{R}}^{n}$. After the modeling section, we have established a population dynamics in form of a differential equation system (8). Generalizing the system, we denote time by t, state variable by x(t), unknown parameters by p, control parameters by q, control functions by u(t), the right hand side of system (8) by f, the constraints by g. We have a problem:

$$\begin{array}{rcl} \begin{array}{rl} \dot{x}(t) =&f(t,x(t),p,q,u(t)),\quad t \in [{t}^{0},{t}^{f}], \\ 0 =&g(x({t}^{0}),p,q).\\ \end{array} & &\end{array}$$

(9)

For all parameter estimation problems, we need data. It is assumed that experiments $i,i = 1,\ldots,N$ have been carried out at the given times ${t}^{j},j = 1,\ldots,M$, yielding measurements η _ij . On the other hand, measurement errors are $\epsilon _{ij}$ and the “true” model response corresponding to these measurements are b _ij :

$$\eta _{ij} = b_{ij}({t}^{j}\!\!,x({t}^{j}),p) + \epsilon _{ ij}.$$

Parameter p is found by minimizing the deviation between data and model response. Due to statistical reasons, some weights $\sigma _{ij}^{-1}$ can be introduced, see details in [3]. In addition, if we know in advance certain information about some approximate value p ₀ of parameter p then we can add a regularization term $\delta {(p - p_{0})}^{2}$ to the objective function. Vector δ has the same dimension as vector p and all components δ^l are nonnegative.

Summing up, a general parameter estimation problem can be formulated as:

$$\begin{array}{rcl} \begin{array}{rl} \min _{(x,p)} & \left [\displaystyle{\sum \limits_{i,j}}{\left (\frac{\eta _{ij}-b_{ij}({t}^{j}\!\!,x({t}^{j}),p)} {\sigma _{ij}} \right )}^{2} +\displaystyle{\sum \limits_{l}}{\delta }^{l}{({p}^{l} - p_{0}^{l})}^{2}\right ]\!, \\ \text{s.t. }(x,p)&\text{ solves equation (9)}.\end{array} & &\end{array}$$

(10)

In our case, we have one experiment (i = 1) with all observation data η _j about the state variables x(t _j ) and the weights σ _j . The unknown parameters are given in Table 2

$$p = (k_{r},k_{\beta },b_{2s},b_{2i},b_{2},i_{2},b_{pn},b_{pr},k_{d}).$$

The initial values for the state variables, which are implied by g, are given at t = t ⁰. In the parameter estimation problem, all the control factors are given, we are interested in finding p.

After parameter estimation, values for the parameters are determined. Now we can consider simulations. Unlike before, the control parameters (q) play the key roles. They are the proportion of full treatment (α), the drug wash-out duration (d) and the treatment efficacy e. To each simulation, there is a fixed set of values. With different values of control parameters, we need to solve the differential equation (8) to compute the simulation.

For parameter estimation and simulations, we use software package VPLAN, see [9] and references therein. VPLAN is a software package developed at the Interdisciplinary Center for Scientific Computing (IWR), University of Heidelberg.

3.4 Result of Parameter Estimation

In this part we are going to present the estimation results. As mentioned before, to minimize the residual, we take into account all parameters in form of piecewise constant functions. We divide the domain into an appropriate number of intervals and find parameter values in each interval. To be more specific, we solve problem (10) in the first interval, then pass the last state variable values as the initial values of the next intervals. This assures the continuity of the solutions. The results of p in all intervals form piecewise constant functions, see Fig. 4.

Fig. 4

The fitted parameters at the study time (2004). The horizontal axes are time axes, unit 5 days

In addition, we use multiple shooting [3] and maximize the usage of data information to deliver a good fit, see Fig. 3. Since parasite populations are very large compared to the host populations, we scale them by 1 ∕ 10¹⁰.

As we can see in the Fig. 3, all the predicted populations (the dashed curves) are in good agreement with data (the points) from Cisse, Burkina Faso. The different scales between hosts and parasites were taken into account by using a weighted least squares function. Due to technical reasons, in some place we use small regularization factors (see the problem setup 3.3). When summing up, the overall residual is very low.

For clear visibility, we show only half of the data points. The study was carried out from the end of 2003 to the end of 2004. Since data at the beginning and closing periods were not very good, so we only take the part from middle of January to November 2004, around 300 days or 60 units of time. There are the peaks in mosquitoes and parasites around August since the season becomes more suitable for vector development. Notice that the eggs can survive through dry season and hatch in rainy season to become larvae, pupae and then mosquitoes.

All the parameters are presented in Fig. 4. It shows that most of the parameters are not constant during the year, they vary a lot due to seasonal conditions, host environments, interactions among different populations.

As expected, the rainy season creates the peaks of mosquito growth rates. There are many more susceptible mosquitoes available compared to dry season. Through the contact with infected humans, they also become infected by parasites. Due to the weather condition, mosquitoes are much more active than in dry months. With Human Land Capture method, volunteers caught many more mosquitoes in rainy months while just a few in the other months [11].

In the same time, the value of k _r has a big drop, indicating that there are almost no recovered people that come back to susceptible class. In malaria, no recovery or complete clearance is expected in a short period of time. We should also mention that patients with low parasite densities sometime are not detected and can be considered healthy. In fact, the parasite density develops slowly and symptoms appear in patients after few weeks or much later than the exposure to mosquitoes. This explains why the peak of selection force of resistance also comes later than the intensive treatment period, this is expressed in the last parameter k _d in Fig. 4.

3.5 Result of Simulation with Controllable Parameters

In this section, we simulate the model (8) using the set of fitted parameters. Here we can control the proportion of full treatment α, the drug regimen corresponding to drug wash-out duration d and the treatment efficacy e. Values of (α, d, e) are varied within certain ranges. We also use VPLAN for solving the differential equation system under different controls.

3.5.1 Proportion of Infected Human Class with Full Treatment

In this part α is our control parameter. This is the proportion of infected human class with full treatment. In this case, two drugs are chosen with treatment efficacy $e\,=\,0.7({\text{time}}^{-1})$, Chloroquine (CQ) with wash-out duration d = 40. 0 and Sulfadoxine-pyrimethamine (SP) with d = 6. 0. Their results turn out to be quite similar. As result of the treatment, the sensitive parasite population is changed much faster than the resistant one.

Simulation in Fig. 5 shows that the proportion of infected humans receiving full medical treatment is very essential in disease control. In addition, the figure indicates that at least a certain proportion of the population needs to be treated properly in order to avoid deadly clinical malaria in the case of very high density of parasites. Recall that we have shown parasite populations with scale 1 ∕ 10¹⁰ and Cisse is only a small town with less than one thousand habitants. We can calculate the average density of parasites in each patient accordingly.

Fig. 5

Simulations of sensitive parasite populations for different proportions of treatments. Increasing α leads to rapid decrease in sensitive parasite population to both treatments. Time unit is 5 days

Beside that, different levels of treatment strongly influence the fitness between sensitive and resistant parasite populations. As we see in Fig. 6, full treatments give resistant parasites a chance to better compete with sensitive parasites to invade the environment.

Fig. 6

Simulations of resistant parasite population for different proportions of treatment. High proportion of full treatment makes resistant parasite population increase faster than low proportion of treatment in the later period. The dashed line represents 60% full treatment with Chloroquine while the solid line represents only 1% Chloroquine full treatment. Time unit is 5 days

3.5.2 Drug Regimens with Different Half-Lives

Using drug regimens with different half-life time would effect the picture of sensitive and resistant parasite populations. This effects the initial ratios of sensitive and resistant populations and also the number of parasites which become adapted to the drug environment. In Cisse–Burkina Faso we do not have any data about different drug usages and how parasites would resist to certain treatment. It is necessary to run virtual simulations with different possible values of parameters d​. For clear comparison, we use the same initial values for the seven populations and keep the same treatment efficacy in all simulations. Assuming that all drug regimens have the same efficacy $e = 0.7({\text{time}}^{-1})$, 80% of infected human receiving full treatment α = 0. 8, different therapies lead to noticeable changes in the resistant parasite population, see Fig. 7.

Fig. 7

Simulations of resistant parasites for different drug half-lives. Switching between different therapies leads to noticeable changes in the number of resistant parasites. Simulations are done for Artesunate (ASU), Quinine (QN), Chloroquine (CQ) with approximated wash-out durations d _ASU  = 0. 04, d _QN  = 0. 5, d _CQ  = 40. 0, based on their average half-lives given in [4]

According to our simulation, for long treatment periods using drugs with shorter half-life gives better performance. However, in the first period of treatment, the different is not much due to the fact that a large proportion of parasites is sensitive to drugs. That is why in this period it does not matter which type of antimalarial drugs are used. The effect shows later, indicated by the fast increase starting from t = 30 in Fig. 7.

We also simulate the case when first Chloroquine is used and afterward switched to Artesunate in the last 3 months of study. As expected, the resistant population was reduced considerably fast, this opens a good chance for alternative treatments.

3.5.3 Different Treatment Policies: Combined Control of α and d

With the setting similar to Burkina Faso, we begin with high efficacies for most of the antimalarial drugs. We simulate here the case when we combine the two mentioned controls, the proportion of full treatment α and the drug type expressed by d. Shortly speaking, we have combined advantages. We can keep both the sensitive and resistant parasite populations under control. The resistant parasite population is relatively small, as we see with Artesunate treatment in the lower panel of Fig. 8. On the upper panel, combined control leads to noticeable change in the infected human population.

Fig. 8

Simulations of resistant parasites and infected humans with different drug treatment policies. Time unit is 5 days

3.5.4 Extended Setting: Different Efficacies of Drug Treatments

In this part we consider the case in which all the infected people can afford their necessary medication or the health care systems are good enough to cover all the cost. So all patients can be treated and α = 1. 0. The treatment efficacy e and drug d are our control parameters. Simulations are done for Chloroquine (CQ), Sunfadioxine-pyrimethamine (SP), Mefloquine (MQ), Artesunate (ASU). The treatment efficacies are close to the values of antimalarial drugs taken from Asia, especially Vietnam. They are based on a report by WHO in [17]. Note that in the Burkina Faso setting, most of the antimalarial medication would begin with high efficacy—since most of the people living in the rural regions have had no access to them before.

Figure 9 using logarithmic scale, lets us easily see that there are big differences between Chloroquine, Sunfadioxine-pyrimethamine, Mefloquine and Artesunate. In the first three drugs, parasite resistance levels in the last period are very high. In contrast, with Artesunate or the similar Artemisinin Combination Therapy, the regimens are still effective, they keep parasite resistance low.

Fig. 9

Simulations of resistant parasites for different treatment efficacies. Simulations are done for Chloroquine (CQ), Sunfadioxine-pyrimethamine (SP), Mefloquine (MQ), Artesunate (ASU) with the values of e are 0. 2, 0. 4, 0. 6, 0. 6 respectively. The wash-out duration d of all drugs is based on [4]: d _ASU  = 0. 04, d _QN  = 0. 5, d _MQ  = 16. 0, d _CQ  = 40. 0. The time unit is 5 days

4 Conclusions

We discuss the simulation results and summarize the works in this paper.

4.1 Interpretation of the Simulation Results

The simulations which have been done with the fitted model lead to the following interpretations:

• From our result, the use of medication do speed up the resistant parasite populations. However, we need them avoid the high (sensitive) parasite density in infected humans, e.g. to keep the average parasite density in human blood below a specific level. Here our model can serve as the potential basis for the control problems, providing an optimal strategy of treatment. We can optimize the proportion (or number) of infected human population which need to be treated with full doses.

• In case of malaria, our model simulations suggest that parasite mutation and drug adaptation both play big roles in resistance. In quantitative sense, the simulation shows that: when drug with long half-life is employed, drug adaption is dominant. This is not the case with short half-life drugs. So the shorter the drug half-life is, the fewer resistant parasites are newly created.

• For the first time of treatment, our simulations show that the outcome of different drug treatments are quite similar. It is explained by the fact that in Burkina Faso, not many people have access to treatment. Most of the drugs are too expensive for the region, especially in a village like Cisse, where our data come from.

  That is why in Burkina Faso or similar regions in Africa, treatment can start with any drug and later switch to a new therapy when the resistant pathogens to the old drugs become dominant. This shows clearly efficacy since most of the parasites which resist to the old drug are sensitive to the new one.

• We also consider different regions with different drug usage. In Asia, antimalarial drugs are sold openly and any person can buy them without prescription from doctors. For most patients, treatment is not their first time. We observe in our simulations that the drug therapies and their efficacies strongly influence the overall treatment results.

By using a quantitative model, we can simulate a lot of scenarios in advance. Depending on preferred criteria, such as keeping the total parasite density below certain threshold or reducing the resistant parasite population, clinicians should be able to choose the suitable therapies. In general, the model results are valid not only for malaria but also for other infectious diseases whose biology are similar to malaria. Based on these conclusions, treatment strategies to reduce drug resistance can be elaborated.

4.2 Summary

To sum up, in this paper we have built a model describing the population dynamics as they appear in vector-borne diseases. In comparison to most of the mathematical models before, our model has two new compartments for parasite populations and includes parameters describing drug treatment.

With numerical study, we have solved parameter estimation and simulation problems. We have obtained fitted parameters and a good agreement with the data in Burkina Faso. We have also simulated the fitted model with controllable parameters. Using the VPLAN package, we were able to solve the systems and to see the influence of drug treatment not only on parasites but also on the host populations.