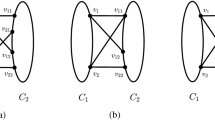
Abstract
Corrádi and Hajnal in 1963 proved the following theorem on the NP-complete problem on the existence of k disjoint cycles in an n-vertex graph G: For all k ≥ 1 and n ≥ 3k, every (simple) n-vertex graph G with minimum degree δ(G) ≥ 2k contains k disjoint cycles. The same year, Dirac described the 3-connected multigraphs not containing two disjoint cycles and asked the more general question: Which (2k − 1)-connected multigraphs do not contain k disjoint cycles? Recently, Kierstead, Kostochka, and Yeager resolved this question. In this paper, we sharpen this result by presenting a description that can be checked in polynomial time of all multigraphs G with no k disjoint cycles for which the underlying simple graph \( \underline {G}\) satisfies the following Ore-type condition: \(d_{ \underline {G}}(v)+d_{ \underline {G}}(u)\geq 4k-3\) for all nonadjacent u, v ∈ V (G).
Dedicated to Gregory Gutin on the occasion of his 60th birthday
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
Dirac used the word graphs, but in [3] this appears to mean multigraphs.
References
H.L. Bodlaender, On disjoint cycles. Int. J. Found. Comput. Sci. 5, 59–68 (1994)
K. Corrádi, A. Hajnal, On the maximal number of independent circuits in a graph. Acta Math. Acad. Sci. Hungar. 14, 423–439 (1963)
G. Dirac, Some results concerning the structure of graphs. Can. Math. Bull. 6, 183–210 (1963)
R.G. Downey, M.R. Fellows Fixed-parameter tractability and completeness. Congr. Numer. 87, 161–178 (1992)
H. Enomoto, On the existence of disjoint cycles in a graph. Combinatorica 18(4), 487–492 (1998)
M.R. Garey, D.S. Johnson, Computers and intractability, in A Guide to the Theory of NP-Completeness. A Series of Books in the Mathematical Sciences (W. H. Freeman and Co., San Francisco, 1979), x+338 pp. (p. 68)
H.A. Kierstead, A.V. Kostochka, Ore-type versions of Brooks’ theorem. J. Comb. Theory Ser. B 99, 298–305 (2009)
H. Kierstead, A. Kostochka, T. Molla, E.C. Yeager, Sharpening an Ore-type version of the Corrádi-Hajnal theorem. Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg, published online (2016)
H.A. Kierstead, A.V. Kostochka, E.C. Yeager, On the Corrádi-Hajnal theorem and a question of dirac. J. Comb. Theory Ser. B 122, 121–148 (2017)
H.A. Kierstead, A.V. Kostochka, E.C. Yeager, The (2k − 1)-connected multigraphs with at most k − 1 disjoint cycles. Combinatorica 37(1), 77–86 (2017)
A.V. Kostochka, L. Rabern, M. Stiebitz, Graphs with chromatic number close to maximum degree. Discret. Math. 312, 1273–1281 (2012)
L. Lovász, On graphs not containing independent circuits, (Hungarian. English summary) Mat. Lapok 16, 289–299 (1965)
S. Micali, V. Vazirani, An \(O(\sqrt {|V|} \cdot |E|)\) algorithm for finding a maximum matching in general graphs, in Proceedings of Twenty-first Annual Symposium on Foundations of Computer Science (IEEE Berkeley, California, 1980), pp. 17–27
L. Rabern, A-critical graphs with small high vertex cliques. J. Comb. Theory Ser. B 102, 126–130 (2012)
H. Wang, On the maximum number of disjoint cycles in a graph. Discret. Math. 205, 183–190 (1999)
Acknowledgements
We thank a referee for a number of helpful comments. Research of A. Kostochka is supported in part by NSF grant DMS-1600592 and by grants 18-01-00353A and 16-01-00499 of the Russian Foundation for Basic Research. Research of T. Molla is supported in part by NSF grant DMS-1500121. Research of D. Yager is supported by the Campus Research Board of the University of Illinois.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this chapter
Cite this chapter
Kierstead, H.A., Kostochka, A.V., Molla, T., Yager, D. (2018). An Algorithmic Answer to the Ore-Type Version of Dirac’s Question on Disjoint Cycles. In: Goldengorin, B. (eds) Optimization Problems in Graph Theory. Springer Optimization and Its Applications, vol 139. Springer, Cham. https://doi.org/10.1007/978-3-319-94830-0_8
Download citation
DOI: https://doi.org/10.1007/978-3-319-94830-0_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-94829-4
Online ISBN: 978-3-319-94830-0
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)