Fine-Grained Complexity of Safety Verification

Abstract

We study the fine-grained complexity of Leader Contributor Reachability ($\mathsf {LCR}$) and Bounded-Stage Reachability (${\mathsf {BSR}}$), two variants of the safety verification problem for shared-memory concurrent programs. For both problems, the memory is a single variable over a finite data domain. We contribute new verification algorithms and lower bounds based on the Exponential Time Hypothesis (${\mathsf {ETH}}$) and kernels.

$\mathsf {LCR}$ is the question whether a designated leader thread can reach an unsafe state when interacting with a certain number of equal contributor threads. We suggest two parameterizations: (1) By the size of the data domain $\texttt {D}$ and the size of the leader $\texttt {L}$, and (2) by the size of the contributors $\texttt {C}$. We present two algorithms, running in $\mathcal {O}^*((\texttt {L}\cdot (\texttt {D}+1))^{\texttt {L}\cdot \texttt {D}} \cdot \texttt {D}^{\texttt {D}})$ and $\mathcal {O}^*(4^{\texttt {C}})$ time, showing that both parameterizations are fixed-parameter tractable. Further, we suggest a modification of the first algorithm suitable for practical instances. The upper bounds are complemented by (matching) lower bounds based on ${\mathsf {ETH}}$ and kernels.

For ${\mathsf {BSR}}$, we consider programs involving $\texttt {t}$ different threads. We restrict the analysis to computations where the write permission changes s times between the threads. ${\mathsf {BSR}}$ asks whether a given configuration is reachable via such an s-stage computation. When parameterized by $\texttt {P}$, the maximum size of a thread, and $\texttt {t}$, the interesting observation is that the problem has a large number of difficult instances. Formally, we show that there is no polynomial kernel, no compression algorithm that reduces $\texttt {D}$ or s to a polynomial dependence on $\texttt {P}$ and $\texttt {t}$. This indicates that symbolic methods may be harder to find for this problem.

A full version of the paper is available as [9].

1 Introduction

We study the fine-grained complexity of two safety verification problems [1, 16, 27] for shared-memory concurrent programs. The motivation to reconsider these problems are recent developments in fine-grained complexity theory [6, 10, 30, 33]. They suggest that classifications such as $\mathsf {NP}$ or even $\mathsf {FPT}$ are too coarse to explain the success of verification methods. Instead, it should be possible to identify the precise influence that parameters of the input have on the verification time. Our contribution confirms this idea. We give new verification algorithms for the two problems that, for the first time, can be proven optimal in the sense of fine-grained complexity theory. To state the results, we need some background. As we proceed, we explain the development of fine-grained complexity theory.

There is a well-known gap between the success that verification tools see in practice and the judgments about computational hardness that worst-case complexity is able to give. The applicability of verification tools steadily increases by tuning them towards industrial instances. The complexity estimation is stuck with considering the input size (or at best assumes certain parameters to be constant, which does not mean much if the runtime is then $n^k$, where n is the input size and k the parameter).

The observation of a gap between practical algorithms and complexity theory is not unique to verification but made in every field that has to solve computationally hard problems. Complexity theory has taken up the challenge to close the gap. So-called fixed-parameter tractability (${\mathsf {FPT}}$) [11, 13] proposes to identify parameters k so that the runtime is $f(k) poly (n)$, where f is a computable function. These parameters are powerful in the sense that they dominate the complexity.

For an ${\mathsf {FPT}}$ result to be useful, function f should only be mildly exponential, and of course k should be small in the instances of interest. Intuitively, they are what one needs to optimize. Fine-grained complexity is the study of upper and lower bounds on function f. Indeed, the fine-grained complexity of a problem is written as $O^*(f(k))$, emphasizing f and k and suppressing the polynomial part. For upper bounds, the approach is still to come up with an algorithm.

For lower bounds, fine-grained complexity has taken a new and very pragmatic perspective. For the problem of n-variable ${\mathsf {3}\text {-}\mathsf {SAT}}$ the best known algorithm runs in $2^n$, and this bound has not been improved since 1970. The idea is to take improvements on this problem as unlikely, known as the exponential-time hypothesis (${\mathsf {ETH}}$) [30]. ${\mathsf {ETH}}$ serves as a lower bound that is reduced to other problems [33]. An even stronger assumption about n-variable ${{\mathsf {SAT}}}$, called ${\mathsf {SETH}}$ [6, 30], and a similar one about Set Cover [10] allow for lower bounds like the absence of $(2-\varepsilon )^n$ algorithms.

In this work, we contribute fine-grained complexity results for verification problems on concurrent programs. The first problem is reachability for a leader thread that is interacting with an unbounded number of contributors (${\mathsf {LCR}}$) [16, 27]. We show that, assuming a parameterization by the size of the leader $\texttt {L}$ and the size of the data domain $\texttt {D}$, the problem can be solved in $\mathcal {O}^*((\texttt {L}\cdot (\texttt {D}+1))^{\texttt {L}\cdot \texttt {D}} \cdot \texttt {D}^{\texttt {D}})$. At the heart of the algorithm is a compression of computations into witnesses. To check reachability, our algorithm then iterates over candidates for witnesses and checks each of them for being a proper witness. Interestingly, we can formulate a variant of the algorithm that seems to be suited for large state spaces.

Using ${\mathsf {ETH}}$, we show that the algorithm is (almost) optimal. Moreover, the problem is shown to have a large number of hard instances. Technically, there is no polynomial kernel [4, 5]. Experience with kernel lower bounds is still limited. This notion of hardness seems to indicate that symbolic methods are hard to apply to the problem. The lower bounds that we present share similarities with the reductions from [7, 24, 25].

If we consider the size of the contributors a parameter, we obtain a singly exponential upper bound that we also prove to be tight. The saturation-based technique that we use is inspired by thread-modular reasoning [20, 21, 26, 29].

The second problem we study generalizes bounded context switching. Bounded-stage reachability (${\mathsf {BSR}}$) asks whether a state is reachable if there is a bound s on the number of times the write permission is allowed to change between the threads [1]. Again, we show the new form of kernel lower bound. The result is tricky and highlights the power of the computation model.

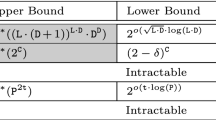
The results are summarized by the table below. Two findings stand out, we highlight them in gray. We present a new algorithm for ${\mathsf {LCR}}$. Moreover, we suggest kernel lower bounds as hardness indicators for verification problems. The lower bound for ${\mathsf {BSR}}$ is particularly difficult to achieve.

Related Work. Concurrent programs communicating through a shared memory and having a fixed number of threads have been extensively studied [2, 14, 22, 28]. The leader contributor reachability problem as considered in this paper was introduced as parametrized reachability in [27]. In [16], it was shown to be ${\mathsf {NP}}$-complete when only finite-state programs are involved and ${\mathsf {PSPACE}}$-complete for recursive programs. In [31], the parameterized pairwise-reachability problem was considered and shown to be decidable. Parameterized reachability under a variant of round-robin scheduling was proven decidable in [32].

The bounded-stage restriction on the computations of concurrent programs as considered here was introduced in [1]. The corresponding reachability problem was shown to be ${\mathsf {NP}}$-complete when only finite-state programs are involved. The problem remains in $\mathsf {NEXP}$-time and ${\mathsf {PSPACE}}$-hard for a combination of counters and a single pushdown. The bounded-stage restriction generalizes the concept of bounded context switching from [34], which was shown to be ${\mathsf {NP}}$-complete in that paper. In [8], ${\mathsf {FPT}}$ algorithms for bounded context switching were obtained under various parameterization. In [3], networks of pushdowns communicating through a shared memory were analyzed under various topological restrictions.

There have been few efforts to obtain fixed-parameter-tractable algorithms for automata and verification-related problems. ${\mathsf {FPT}}$ algorithms for automata problems have been studied in [18, 19, 35]. In [12], model-checking problems for synchronized executions on parallel components were considered and proven intractable. In [15], the notion of conflict serializability was introduced for the TSO memory model and an ${\mathsf {FPT}}$ algorithm for checking serializability was provided. The complexity of predicting atomicity violations on concurrent systems was considered in [17]. The finding is that ${\mathsf {FPT}}$ solutions are unlikely to exist.

2 Preliminaries

We introduce our model for programs, which is fairly standard and taken from [1, 16, 27], and give the basics on fixed-parameter tractability.

Programs. A program consists of finitely many threads that access a shared memory. The memory is modeled to hold a single value at a time. Formally, a (shared-memory) program is a tuple $\mathcal {A}= ( D , a^0, (P_i)_{i \in [1..t]})$. Here, $D$ is the data domain of the memory and $a^0\in D$ is the initial value. Threads are modeled as control-flow graphs that write values to or read values from the memory. These operations are captured by $Op ( D ) = \lbrace !a, ?a \mid a \in D \rbrace$. We use the notation $W ( D ) = \lbrace !a \mid a \in D \rbrace$ for the write operations and $R ( D ) = \lbrace ?a \mid a \in D \rbrace$ for the read operations. A thread $P_{id}$ is a non-deterministic finite automaton $( Op ( D ), Q, q^0, \delta )$ over the alphabet of operations. The set of states is Q with $q^0\in Q$ the initial state. The final states will depend on the verification task. The transition relation is $\delta \subseteq Q \times ( Op ( D ) \cup \{ \varepsilon \}) \times Q$. We extend it to words and also write $q \xrightarrow {w} q'$ for $q' \in \delta (q,w)$. Whenever we need to distinguish between different threads, we add indices and write $Q_{id}$ or $\delta _{id}$.

The semantics of a program is given in terms of labeled transitions between configurations. A configuration is a pair $( pc , a) \in (Q_1 \times \dots \times Q_t) \times D$. The program counter $pc$ is a vector that shows the current state $pc (i)\in Q_i$ of each thread $P_i$. Moreover, the configuration gives the current value in memory. We call $c^0 = ( pc ^0, a^0)$ with $pc ^0(i)=q^0_i$ for all $i\in [1..t]$ the initial configuration. Let C denote the set of all configurations. The transition relation among configurations $\rightarrow \ \subseteq C\times ( Op ( D )\cup \lbrace \varepsilon \rbrace )\times C$ is obtained by lifting the transition relations of the threads. To define it, let $pc _1 = pc [i=q_i]$, meaning thread $P_i$ is in state $q_i$ and otherwise the program counter coincides with $pc$. Let $pc _2= pc [i=q_i']$. If thread $P_i$ tries to read with the transition $q_i \xrightarrow {?a} q_i'$, then $( pc _1, a)\xrightarrow {?a}( pc _2, a)$. Note that the memory is required to hold the desired value. If the thread has the transition $q_i\xrightarrow {!b} q_i'$, then $( pc _1, a)\xrightarrow {!b}( pc _2, b)$. Finally, $q_i\xrightarrow {\varepsilon }q_i'$ yields $( pc _1, a)\xrightarrow {\varepsilon }( pc _2, a)$. The program’s transition relation is generalized to words, $c \xrightarrow {w} c'$. We call such a sequence of consecutive labeled transitions a computation. To indicate that there is a word that justifies a computation from c to $c'$, we write $c \rightarrow ^* c'$. We may use an index $\xrightarrow {w}_i$ to indicate that the computation was induced by thread $P_i$. Where appropriate, we also use the program as an index, $\xrightarrow {w}_\mathcal {A}$.

Fixed-Parameter Tractability. We wish to study the fine-grained complexity of safety verification problems for the above programs. This means our goal is to identify parameters of these problems that have two properties. First, in practical instances they are small. Second, assuming that these parameters are small, show that there are efficient verification algorithms. Parametrized complexity makes precise the idea of an algorithm being efficient relative to a parameter.

A parameterized problem L is a subset of $\varSigma ^*\times \mathbb N$. The problem is fixed-parameter tractable if there is a deterministic algorithm that, given $(x,k)\in \varSigma ^*\times \mathbb {N}$, decides $(x,k)\in L$ in time $f(k)\cdot |x|^{O(1)}$. We use ${\mathsf {FPT}}$ for the class of all fixed-parameter-tractable problems and say a problem is ${\mathsf {FPT}}$ to mean it is in that class. Note that f is a computable function that only depends on the parameter k. It is common to denote the runtime by $\mathcal {O}^*(f(k))$ and suppress the polynomial part. We will be interested in the precise dependence on the parameter, in upper and lower bounds on the function f. This study is often referred to as fine-grained complexity.

Lower bounds on f are obtained by the Exponential Time Hypothesis (${\mathsf {ETH}}$). It assumes that there is no algorithm solving n-variable ${\mathsf {3}\text {-}\mathsf {SAT}}$ in $2^{o(n)}$ time. The reasoning is as follows: If f dropped below a certain bound, ${\mathsf {ETH}}$ would fail.

While many parameterizations of ${\mathsf {NP}}$-hard problems were proven to be fixed-parameter tractable, there are problems that are unlikely to be ${\mathsf {FPT}}$. Such problems are hard for the complexity class $\mathsf {W}[1]$. The appropriate notion of reduction for a theory of relative hardness in parameterized complexity is called parameterized reduction.

3 Leader Contributor Reachability

We consider the leader contributor reachability problem for shared-memory programs. The problem was introduced in [27] and shown to be ${\mathsf {NP}}$-complete in [16] for the finite-state case.¹ We contribute two new verification algorithms that target two parameterizations of the problem. In both cases, our algorithms establish fixed-parameter tractability. Moreover, with matching lower bounds we prove them to be optimal even in the fine-grained sense.

An instance of the leader contributor reachability problem is given by a shared-memory program of the form $\mathcal {A}= ( D , a^0, (P_L, (P_i)_{i \in [1..t]}))$. The program has a designated leader thread $P_L$ and several contributor threads $P_1, \dots , P_t$. In addition, we are given a set of unsafe states for the leader. The task is to check whether the leader can reach an unsafe state when interacting with a number of instances of the contributors. It is worth noting that the problem can be reduced to having a single contributor. Let the corresponding thread $P_C$ be the union of $P_1, \dots , P_t$ (constructed using an initial $\varepsilon$-transition). We base our complexity analysis on this simplified formulation of the problem.

For the definition, let $\mathcal {A}= ( D , a^0, (P_L,P_C))$ be a program with two threads. Let $F_L \subseteq Q_L$ be a set of unsafe states of the leader. For $t \in \mathbb {N}$, define the program $\mathcal {A}^t = ( D , a^0, (P_L, (P_C)_{i\in [1..t]} ))$ to have t copies of $P_C$. Further, let $C^f$ be the set of configurations where the leader is in an unsafe state (from $F_L$). The problem of interest is as follows:

We consider two parameterizations of ${\mathsf {LCR}}$. First, we parameterize by $\texttt {D}$, the size of the data domain $D$, and $\texttt {L}$, the number of states of the leader $P_L$. We denote the parameterization by ${\mathsf {LCR}(\texttt {D}, \texttt {L})}$. While for ${\mathsf {LCR}(\texttt {D}, \texttt {L})}$ we obtain an ${\mathsf {FPT}}$ algorithm, it is not likely that ${\mathsf {LCR}(\texttt {D})}$ and ${\mathsf {LCR}(\texttt {L})}$ admit the same. These parameterizations are $\mathsf {W}[1]$-hard. For details, we refer to the full version [9].

The second parameterization that we consider is ${\mathsf {LCR}(\texttt {C})}$, a parameterization by the number of states of the contributor $P_C$. We prove that the parameter is enough to obtain an ${\mathsf {FPT}}$ algorithm.

3.1 Parameterization by Memory and Leader

We give an algorithm that solves ${\mathsf {LCR}}$ in time $\mathcal {O}^*( (\texttt {L}\cdot (\texttt {D}+ 1))^{\texttt {L}\cdot \texttt {D}} \cdot \texttt {D}^{\texttt {D}} )$, which means ${\mathsf {LCR}(\texttt {D}, \texttt {L})}$ is ${\mathsf {FPT}}$. We then show how to modify the algorithm to solve instances of ${\mathsf {LCR}}$ as they are likely to occur in practice. Interestingly, the modified version of the algorithm lends itself to an efficient implementation based on off-the-shelf sequential model checkers. We conclude with lower bounds for ${\mathsf {LCR}(\texttt {D}, \texttt {L})}$.

Upper Bound. We give an algorithm for the parameterization ${\mathsf {LCR}(\texttt {D}, \texttt {L})}$. The key idea is to compactly represent computations that may be present in an instance of the given program. To this end, we introduce a domain of so-called witness candidates. The main technical result, Lemma 4, links computations and witness candidates. It shows that reachability of an unsafe state holds in an instance of the program if and only if there is a witness candidate that is valid (in a precise sense). With this, our algorithm iterates over all witness candidates and checks each of them for being valid. To state the overall result, let $Wit (\texttt {L}, \texttt {D}\,) = \left( \texttt {L}\cdot (\texttt {D}+ 1) \right) ^{\texttt {L}\cdot \texttt {D}} \cdot \texttt {D}^{\texttt {D}} \cdot \texttt {L}$ be the number of witness candidates and let $Valid (\texttt {L}, \texttt {D}, \texttt {C}\,) = \texttt {L}^3 \cdot \texttt {D}^{2} \cdot \texttt {C}^2$ be the time it takes to check validity of a candidate. Note that it is polynomial.

Theorem 1

${\mathsf {LCR}}$ can be solved in time $\mathcal {O}( Wit (\texttt {L}, \texttt {D}\,) \cdot Valid (\texttt {L}, \texttt {D}, \texttt {C}\,) )$.

Let $\mathcal {A}= ( D , a^0, (P_L, P_C))$ be the program of interest and $F_L$ be the set of unsafe states in the leader. Assume we are given a computation $\rho$ showing that $P_L$ can reach a state in $F_L$ when interacting with a number of contributors. We explain the main ideas to find an efficient representation for $\rho$ that still allows for the reconstruction of a similar computation. To simplify the presentation, we assume the leader never writes (!a) and immediately reads (?a) the same value. If this is the case, the read can be replaced by $\varepsilon$.

In a first step, we delete most of the moves in $\rho$ that were carried out by contributors. We only keep first writes. For each value a, this is the write transition $fw (a) = c \xrightarrow {!a} c'$ where a is written by a contributor for the first time. The reason we can omit subsequent writes of a is the following: If $fw (a)$ is carried out by contributor $P_1$, we can assume that there is an arbitrary number of other contributors that all mimicked the behavior of $P_1$. This means whenever $P_1$ did a transition, they copycatted it right away. Hence, there are arbitrarily many contributors pending to write a. Phrased differently, the symbol a is available for the leader whenever $P_L$ needs to read it. The idea goes back to the Copycat Lemma stated in [16]. The reads of the contributors are omitted as well. We will make sure they can be served by the first writes and the moves done by $P_L$.

After the deletion, we are left with a shorter expression $\rho '$. We turn it into a word w over the alphabet $Q_L \cup D _{\bot }\cup \bar{ D }$ with $D _{\bot }= D \cup \lbrace \bot \rbrace$ and $\bar{ D }= \lbrace \bar{a} \mid a \in D \rbrace$. Each transition $c \xrightarrow {!a / ?a / \varepsilon }_L c'$ in $\rho '$ that is due to the leader moving from q to $q'$ is mapped (i) to $q.a.q'$ if it is a write and (ii) to $q.\bot .q'$ otherwise. A first write $fw (a) = c \xrightarrow {a} c'$ of a contributor is mapped to $\bar{a}$. We may assume that the resulting word w is of the form $w = w_1 . w_2$ with $w_1 \in ( ( Q_L . D _{\bot })^* . \bar{ D })^*$ and $w_2 \in (Q_L . D _{\bot })^* . F_L$. Note that w can still be of unbounded length.

In order to find a witness of bounded length, we compress $w_1$ and $w_2$ to $w'_1$ and $w'_2$. Between two first writes $\bar{a}$ and $\bar{b}$ in $w_1$, the leader can perform an unbounded number of transitions, represented by a word in $( Q_L . D _{\bot })^*$. Hence, there are states $q \in Q_L$ repeating between $\bar{a}$ and $\bar{b}$. We contract the word between the first and the last occurrence of q into just a single state q. This state now represents a loop on $P_L$. Since there are $\texttt {L}$ states in the leader, this bounds the number of contractions. Furthermore, we know that the number of first writes is bounded by $\texttt {D}$, each symbol can be written for the first time at most once. Thus, the compressed string $w'_1$ is in the language $( (Q_L. D _{\bot })^{\le \texttt {L}} . \bar{ D })^{\le \texttt {D}}$.

The word $w_2$ is of the form $w_2 = q.u$ for a state $q \in Q_L$ and a word u. We truncate the word u and only keep the state q. Then we know that there is a computation leading from q to a state in $F_L$ where $P_L$ can potentially write any symbol but read only those symbols which occurred as a first write in $w'_1$. Altogether, we are left with a word of bounded length.

Definition 2

The set of witness candidates is $\mathcal {E}= ( (Q_L. D _{\bot })^{\le \texttt {L}} . \bar{ D })^{\le \texttt {D}} . Q_L$.

To characterize computations in terms of witness candidates, we define the notion of validity. This needs some notation. Consider a word $w = w_1 \dots w_\ell$ over some alphabet $\varGamma$. For $i \in [1..\ell ]$, we set $w[i] = w_i$ and $w[1..i] = w_1 \dots w_i$. If $\varGamma ' \subseteq \varGamma$, we use $w \! \downarrow _{\varGamma '}$ for the projection of w to the letters in $\varGamma '$.

Consider a witness candidate $w \in \mathcal {E}$ and let $i \in [1..|w|]$. We use $\bar{ D }(w, i)$ for the set of all first writes that occurred in w up to position i. Formally, $\bar{ D }(w,i) = \lbrace a \mid \bar{a} \text { is a letter in } w[1..i] \! \downarrow _{\bar{ D }} \rbrace$. We abbreviate $\bar{ D }(w, |w|)$ as $\bar{ D }(w)$. Let $q \in Q_L$ and $S \subseteq D$. Recall that the state represents a loop in $P_L$. The set of all letters written within a loop from q to q when reading only symbols from S is ${{\mathrm{\texttt {Loop}}}}(q,S) = \lbrace a \mid a \in D \text { and } \exists v_1, v_2 \in ( W ( D ) \cup R (S))^* : q \xrightarrow {v_1 !a v_2}_L q \rbrace$.

The definition of validity is given next. The three requirements are made precise in the text below.

Definition 3

A witness candidate $w \in \mathcal {E}$ is valid if it satisfies the following properties: (1) First writes are unique. (2) The word w encodes a run in $P_L$. (3) There are supportive computations on the contributors.

• (1) If $w \! \downarrow _{\bar{ D }}\,= \bar{c_1} \dots \bar{c_\ell }$, then the $\bar{c_i}$ are pairwise different.

• (2) Let $w \! \downarrow _{Q_L \cup D _{\bot }} = q_1 a_1 q_2 a_2 \dots a_\ell q_{\ell +1}$. If $a_i \in D$, then $q_i \xrightarrow {!a_i}_L q_{i+1} \in \delta _L$ is a write transition of $P_L$. If $a_i = \bot$, then we have an $\varepsilon$-transition $q_i \xrightarrow {\varepsilon }_L q_{i+1}$. Alternatively, there is a read $q_i \xrightarrow {?a}_L q_{i+1}$ of a symbol $a \in \bar{ D }(w, {{\mathrm{\texttt {pos}}}}(a_i))$ that already occurred within a first write (the leader does not read the own writes). Here, we use ${{\mathrm{\texttt {pos}}}}(a_i)$ to access the position of $a_i$ in w. State $q_1=q^0_L$ is initial. There is a run from $q_{\ell + 1}$ to a state $q_f \in F_L$. During this run, reading is restricted to symbols that occurred as first writes in w. Formally, there is a $v \in ( W ( D ) \cup R (\bar{ D }(w)))^*$ such that $q_{\ell +1} \xrightarrow {v}_L q_f$.

• (3) For each prefix $v\bar{a}$ of w with $\bar{a} \in \bar{ D }$ there is a computation $q^0_C \xrightarrow {u !a}_C q$ on $P_C$ so that the reads in u can be obtained from v. Formally, let $u' = u \! \downarrow _{ R ( D )}$. Then there is an embedding of $u'$ into v, a monotone map $\mu : [1..|u'|] \rightarrow [1..|v|]$ that satisfies the following. Let $u'[i] =\ ?a$ with $a \in D$. The read is served in one of the following three ways. We may have $v[\mu (i)] = a$, which corresponds to a write of a by $P_L$. Alternatively, $v[\mu (i)] = q \in Q_L$ and $a \in {{\mathrm{\texttt {Loop}}}}(q,\bar{ D }(w,\mu (i)))$. This amounts to reading from a leader’s write that was executed in a loop. Finally, we may have $a \in \bar{ D }(w, \mu (i))$, corresponding to reading from another contributor.

Lemma 4

There is a $t \in \mathbb {N}$ so that $c^0\rightarrow ^*_{\mathcal {A}^t}c$ with $c\in C^f$ if and only if there is a valid witness candidate $w \in \mathcal {E}$.

Our algorithm iterates over all witness candidates $w \in \mathcal {E}$ and tests whether w is valid. The number of candidates $Wit (\texttt {L}, \texttt {D})$ is given by $\left( \texttt {L}\cdot (\texttt {D}+ 1) \right) ^{\texttt {L}\cdot \texttt {D}} \cdot \texttt {D}^{\texttt {D}} \cdot \texttt {L}$. This is due to the fact that we can force a witness candidate to have maximum length via inserting padding symbols. The number of candidates constitutes the first factor of the runtime stated in Theorem 1. The polynomial factor $Valid (\texttt {L}, \texttt {D}, \texttt {C})$ is due to the following Lemma. Details are given in the full version of the paper [9].

Lemma 5

Validity of $w \in \mathcal {E}$ can be checked in time $\mathcal {O}( \texttt {L}^3 \cdot \texttt {D}^{\,2} \cdot \texttt {C}^{\,2})$.

Practical Algorithm. We improve the above algorithm so that it should work well on practical instances. The idea is to factorize the leader along its strongly connected components (SCCs), the number of which is assumed to be small in real programs. Technically, our improved algorithm works with valid SCC-witnesses. They symbolically represent SCCs rather than loops in the leader. To state the complexity, we define the straight-line depth, the number of SCCs the leader may visit during a computation. The definition needs a graph construction.

Let $\mathcal {V}\subseteq \bar{ D }^{\le \texttt {D}}$ contain only words that do not repeat letters. Let $r = \bar{c}_1 \dots \bar{c}_\ell \in \mathcal {V}$ and $i \in [0..\ell ]$. By $P_L \! \downarrow _{i}$ we denote the automaton obtained from $P_L$ by removing all transitions that read a value outside $\lbrace c_1, \dots , c_i \rbrace$. Let ${{\mathrm{\texttt {SCC}}}}(P_L \! \downarrow _{i})$ denote the set of all SCCs in this automaton. We construct the directed graph $G(P_L,r)$ as follows. The vertices are the SCCs of all $P_L \! \downarrow _{i}$, $i \in [0..\ell ]$. There is an edge between $S, S' \in {{\mathrm{\texttt {SCC}}}}(P_L \! \downarrow _{i})$, if there are states $q \in S, q' \in S'$ with $q \rightarrow q'$ in $P_L \! \downarrow _{i}$. If $S \in {{\mathrm{\texttt {SCC}}}}(P_L \! \downarrow _{i-1})$ and $S' \in {{\mathrm{\texttt {SCC}}}}(P_L \! \downarrow _{i})$, we only get an edge if we can get from S to $S'$ by reading $c_i$. Note that the graph is acyclic.

The depth d(r) of $P_L$ relative to r is the length of the longest path in $G(P_L,r)$. The straight-line depth is $\texttt {d}= \max \lbrace d(r) \mid r \in \mathcal {V} \rbrace$. The number of SCCs $\texttt {s}$ is the size of ${{\mathrm{\texttt {SCC}}}}(P_L \! \downarrow _{0})$. With these values at hand, the number of SCC-witness candidates (the definition of which can be found in the full version [9]) can be bounded by $Wit_{SCC} (\texttt {s}, \texttt {D}, \texttt {d}) \le (\texttt {s}\cdot (\texttt {D}+ 1))^{\texttt {d}} \cdot \texttt {D}^{\texttt {D}} \cdot 2^{\texttt {D}+ \texttt {d}}$. The time needed to test whether a candidate is valid is $Valid_{SCC} (\texttt {L}, \texttt {D}, \texttt {C}, \texttt {d}) = \texttt {L}^2 \cdot \texttt {D}\cdot \texttt {C}^2 \cdot \texttt {d}^2$.

Theorem 6

${\mathsf {LCR}}$ can be solved in time $\mathcal {O}( Wit_{SCC} (\texttt {s}, \texttt {D}, \texttt {d}) \cdot Valid_{SCC} (\texttt {L}, \texttt {D}, \texttt {C}, \texttt {d}))$.

For this algorithm, what matters is that the leader’s state space is strongly connected. The number of states has limited impact on the runtime.

Lower Bound. We prove that the algorithm from Theorem 1 is only a root factor away from being optimal: A $2^{o( \sqrt{\texttt {L}\cdot \texttt {D}} \cdot \log ( \texttt {L}\cdot \texttt {D}) )}$-time algorithm for ${\mathsf {LCR}}$ would contradict ${\mathsf {ETH}}$. We achieve the lower bound by a reduction from ${\mathsf {k \times k ~ Clique}}$, the problem of finding a clique of size k in a graph the vertices of which are elements of a $k \times k$ matrix. Moreover, the clique has to contain one vertex from each row. Unless ${\mathsf {ETH}}$ fails, the problem cannot be solved in time $2^{o(k \cdot \log (k))}$ [33].

Technically, we construct from an instance (G, k) of ${\mathsf {k \times k ~ Clique}}$ an instance $(\mathcal {A}= ( D , a^0, (P_L, P_C)), F_L)$ of ${\mathsf {LCR}}$ such that $\texttt {D}= \mathcal {O}(k)$ and $\texttt {L}= \mathcal {O}(k)$. Furthermore, we show that G contains the desired clique of size k if and only if there is a $t \in \mathbb {N}$ such that $c^0 \rightarrow ^*_{\mathcal {A}^t} c$ with $c \in C^f$. Suppose we had an algorithm for ${\mathsf {LCR}}$ running in time $2^{o( \sqrt{\texttt {L}\cdot \texttt {D}} \cdot \log ( \texttt {L}\cdot \texttt {D}) )}$. Combined with the reduction, this would yield an algorithm for ${\mathsf {k \times k ~ Clique}}$ with runtime $2^{o(\sqrt{k^2} \cdot \log (k^2))} = 2^{o(k \cdot \log k)}$. But unless ${\mathsf {ETH}}$ fails, such an algorithm cannot exist.

Proposition 7

${\mathsf {LCR}}$ cannot be solved in time $2^{o( \sqrt{\texttt {L}\cdot \texttt {D}} \cdot \log ( \texttt {L}\cdot \texttt {D}) )}$ unless ${\mathsf {ETH}}$ fails.

We assume that the vertices V of G are given by tuples (i, j) with $i,j \in [1..k]$, where i denotes the row and j denotes the column. In the reduction, we need the leader and the contributors to communicate on the vertices of G. However, we cannot store tuples (i, j) in the memory as this would cause a quadratic blow-up $\texttt {D}= \mathcal {O}(k^2)$. Instead, we communicate a vertex (i, j) as a string ${{\mathrm{\texttt {row}}}}(i).{{\mathrm{\texttt {col}}}}(j)$. We distinguish between row and column symbols to avoid stuttering, the repeated reading of the same symbol. With this, it cannot happen that a thread reads a row symbol twice and takes it for a column.

The program starts its computation with each contributor choosing a vertex (i, j) to store. For simplicity, we denote a contributor storing (i, j) by $P_{(i,j)}$. Note that there can be copies of $P_{(i,j)}$.

Since there are arbitrarily many contributors, the chosen vertices are only a superset of the clique we want to find. To cut away the false vertices, the leader $P_L$ guesses for each row the vertex belonging to the clique. To this end, the program performs for each $i \in [1..k]$ the following steps: If $(i,j_i)$ is the vertex of interest, $P_L$ first writes ${{\mathrm{\texttt {row}}}}(i)$ to the memory. Each contributor that is still active reads the symbol and moves on for one state. Then $P_L$ communicates the column by writing ${{\mathrm{\texttt {col}}}}(j_i)$. Again, the active contributors $P_{(i',j')}$ read.

A contributor can react to the read symbol in three different ways: (1) If $i' \ne i$, the contributor $P_{(i',j')}$ stores a vertex of a different row. The computation in $P_{(i',j')}$ can only go on if $(i',j')$ is connected to $(i,j_i)$ in G. Otherwise it will stop. (2) If $i' = i$ and $j' = j_i$, then $P_{(i',j')}$ stores exactly the vertex guessed by $P_L$. In this case, $P_{(i',j')}$ can continue its computation. (3) If $i' = i$ and $j' \ne j$, thread $P_{(i',j')}$ stores a different vertex from row i. The contributor has to stop its computation.

After k such rounds, there are only contributors left that store vertices guessed by $P_L$. Furthermore, each two of these vertices are connected. Hence, they form a clique. To transmit this information to $P_L$, each $P_{(i,j_i)}$ writes $\#_i$ to the memory, a special symbol for row i. After $P_L$ has read the string $\#_1 \dots \#_k$, it moves to its final state. A formal construction can be found in the full version [9].

Absence of a Polynomial Kernel. A kernelization of a parameterized problem is a compression algorithm. Given an instance, it returns an equivalent instance the size of which is bounded by a function only in the parameter. From an algorithmic perspective, kernels put a bound on the number of hard instances of the problem. Indeed, the search for small kernels is a key interest in algorithmics, similar to the search for fast ${\mathsf {FPT}}$ algorithms. Even more, it can be shown that kernels exist if and only if a problem admits an ${\mathsf {FPT}}$ algorithm [11].

Let Q be a parameterized problem. A kernelization of Q is an algorithm that transforms, in polynomial time, a given instance (B, k) into an equivalent instance $(B', k')$ such that $|B'| + k' \le g(k)$, where g is a computable function. If g is a polynomial, we say that Q admits a polynomial kernel.

Unfortunately, for many problems the community failed to come up with polynomial kernels. This lead to the contrary approach, namely disproving their existence [4, 5, 23]. Such a result constitutes an exponential lower bound on the number of hard instances. Like computational hardness results, such a bound is seen as an indication of general hardness of the problem. Technically, the existence of a polynomial kernel for the problem of interest is shown to imply $\mathsf {NP}\subseteq \mathsf {co}\mathsf {NP}/ {\mathsf {poly}}$. But this inclusion is unlikely as it would cause a collapse of the polynomial hierarchy to the third level [36].

In order to link the occurrence of a polynomial kernel for ${\mathsf {LCR}(\texttt {D}, \texttt {L})}$ with the above inclusion, we follow the framework developed in [5]. Let $\varGamma$ be an alphabet. A polynomial equivalence relation is an equivalence relation $\mathcal {R}$ on $\varGamma ^*$ with the following properties: Given $x,y \in \varGamma ^*$, it can be decided in time polynomial in $|x| + |y|$ whether $(x,y) \in \mathcal {R}$. Moreover, for each n there are at most polynomially many equivalence classes in $\mathcal {R}$ restricted to $\varGamma ^{\le n}$.

The key tool for proving kernel lower bounds are cross-compositions: Let $L \subseteq \varGamma ^*$ be a language and $Q \subseteq \varGamma ^* \times \mathbb {N}$ be a parameterized language. We say that L cross-composes into Q if there exists a polynomial equivalence relation $\mathcal {R}$ and an algorithm $\mathcal {C}$, the cross-composition, with the following properties: $\mathcal {C}$ takes as input $\varphi _1, \dots , \varphi _I \in \varGamma ^*$, all equivalent under $\mathcal {R}$. It computes in time polynomial in $\sum _{\ell =1}^{I} |\varphi _\ell |$ a string $(y,k) \in \varGamma ^* \times \mathbb {N}$ such that $(y,k) \in Q$ if and only if there is an $\ell \in [1..I]$ with $\varphi _\ell \in L$. Furthermore, $k \le p(\max _{\ell \in [1..I]} |\varphi _\ell | + \log (I) )$ for a polynomial p.

It was shown in [5] that a cross-composition of any ${\mathsf {NP}}$-hard language into a parameterized language Q prohibits the existence of a polynomial kernel for Q unless ${\mathsf {NP}\subseteq \mathsf {co}\mathsf {NP}/ {\mathsf {poly}}}$. In order to make use of this result, we show how to cross-compose ${\mathsf {3}\text {-}\mathsf {SAT}}$ into ${\mathsf {LCR}(\texttt {D}, \texttt {L})}$. This yields the following:

Theorem 8

${\mathsf {LCR}(\texttt {D}, \texttt {L})}$ does not admit a poly. kernel unless ${\mathsf {NP}\subseteq \mathsf {co}\mathsf {NP}/ {\mathsf {poly}}}$.

The difficulty of finding a cross-composition is in the restriction on the size of the parameters. This affects $\texttt {D}$ and $\texttt {L}$: Both parameters are not allowed to depend polynomially on I, the number of given ${\mathsf {3}\text {-}\mathsf {SAT}}$-instances. We resolve the polynomial dependence by encoding the choice of a ${\mathsf {3}\text {-}\mathsf {SAT}}$-instance into the contributors via a binary tree.

Proof

(Idea). Assume some encoding of Boolean formulas as strings over a finite alphabet. We use the polynomial equivalence relation $\mathcal {R}$ defined as follows: Two strings $\varphi$ and $\psi$ are equivalent under $\mathcal {R}$ if both encode ${\mathsf {3}\text {-}\mathsf {SAT}}$-instances, and the numbers of clauses and variables coincide. On strings of bounded length, $\mathcal {R}$ has polynomially many equivalence classes.

Let the given ${\mathsf {3}\text {-}\mathsf {SAT}}$-instances be $\varphi _1, \dots , \varphi _I$. Every two of them are equivalent under $\mathcal {R}$. This means that all $\varphi _\ell$ have the same number of clauses m and use the same set of variables $\lbrace x_1, \dots , x_n \rbrace$. We assume that $\varphi _\ell = C^\ell _1 \wedge \dots \wedge C^\ell _m$.

We construct a program proceeding in three phases. First, it chooses an instance $\varphi _\ell$, then it guesses a valuation for all variables, and in the third phase it verifies that the valuation satisfies $\varphi _\ell$. While the second and the third phase do not cause a dependence of the parameters on I, the first phase does. It is not possible to guess a number $\ell \in [1..I]$ and communicate it via the memory as this would provoke a polynomial dependence of $\texttt {D}$ on I.

To implement the first phase without a polynomial dependence, we transmit the indices of the ${\mathsf {3}\text {-}\mathsf {SAT}}$-instances in binary. The leader guesses and writes tuples $(u_1, 1), \dots , (u_{\log (I)}, \log (I))$ with $u_\ell \in \lbrace 0,1 \rbrace$ to the memory. This amounts to choosing an instance $\varphi _\ell$ with binary representation ${{\mathrm{\texttt {bin}}}}(\ell ) = u_1 \dots u_{\log (I)}$.

It is the contributors’ task to store this choice. Each time, the leader writes a tuple $(u_i,i)$, the contributors read and branch either to the left, if $u_i = 0$, or to the right, if $u_i = 1$. Hence, in the first phase, the contributors are binary trees with I leaves, each leaf storing the index of an instance $\varphi _\ell$. Since we did not assume that I is a power of 2, there may be computations arriving at leaves that do not represent proper indices. In this case, the computation deadlocks.

The size of $D$ and $P_L$ in the first phase is $\mathcal {O}(\log (I))$. This satisfies the size-restrictions of a cross-composition.

For guessing the valuation in the second phase, the system communicates on tuples $(x_i, v)$ with $i \in [1..n]$ and $v \in \lbrace 0,1 \rbrace$. The leader guesses such a tuple for each variable and writes it to the memory. Any participating contributor is free to read one of the tuples. After reading, it stores the variable and the valuation.

In the third phase, the satisfiability check is performed as follows: Each contributor that is still active has stored in its current state the chosen instance $\varphi _\ell$, a variable $x_i$, and its valuation $v_i$. Assume that $x_i$ when evaluated to $v_i$ satisfies $C^\ell _j$, the j-th clause of $\varphi _\ell$. Then the contributor loops in its current state while writing the symbol $\#_j$. The leader waits to read the string $\#_1 \dots \#_m$. If $P_L$ succeeds, we are sure that the m clauses of $\varphi _\ell$ were satisfied by the chosen valuation. Thus, $\varphi _\ell$ is satisfiable and $P_L$ moves to its final state. For details of the construction, we refer to the full version of the paper [9].    $\square$

3.2 Parameterization by Contributors

We show that the size of the contributors $\texttt {C}$ has a wide influence on the complexity of ${\mathsf {LCR}}$. We give an algorithm singly exponential in $\texttt {C}$, provide a matching lower bound, and prove the absence of a polynomial kernel.

Upper Bound. Our algorithm is based on saturation. We keep the states reachable by the contributors in a set and saturate it. This leads to a more compact representation of the program. Technically, we reduce ${\mathsf {LCR}}$ to a reachability problem on a finite automaton. The result is as follows.

Proposition 9

${\mathsf {LCR}}$ can be solved in time $\mathcal {O}(4^{\texttt {C}} \cdot \texttt {L}^4 \cdot \texttt {D}^{\,3} \cdot \texttt {C}^{\,2})$.

The main observation is that keeping one set of states for all contributors suffices to represent a computation. Let $S \subseteq Q_C$ be the set of states reachable by the contributors in a given computation. By the Copycat Lemma [16], we can assume for each $q \in S$ an arbitrary number of contributors that are currently in state q. This means that we do not have to distinguish between different contributor instances.

Formally, we reduce the search space to $Q_L \times D \times \mathcal {P}(Q_C)$. Instead of storing explicit configurations, we store tuples $(q_L, a, S)$, where $q_L \in Q_L$, $a \in D$, and $S \subseteq Q_C$. Between such tuples, the transition relation is as follows. Transitions of the leader change the state and the memory as expected. The contributors also change the memory but saturate S instead of changing the state. Formally, if there is a transition from $q \in S$ to $q'$, we add $q'$ to S.

Lemma 10

There is a $t \in \mathbb {N}$ so that $c^0 \rightarrow ^*_{\mathcal {A}^t} c$ with $c \in C^f$ if and only if there is a run from $(q^0_L, a^0, \lbrace q^0_C \rbrace )$ to a state in $F_L \times D \times \mathcal {P}(Q_C)$.

The dominant factor in the complexity estimation of Proposition 9 is the time needed to construct the state space. It takes time $\mathcal {O}(4^{\texttt {C}} \cdot \texttt {L}^4 \cdot \texttt {D}^{3} \cdot \texttt {C}^{2})$. For the definition and the proof of Lemma 10, we refer to the full version [9].

Lower Bound and Absence of a Polynomial Kernel. We present two lower bounds for ${\mathsf {LCR}}$. The first is based on ${\mathsf {ETH}}$: We show that there is no $2^{o(\texttt {C})}$-time algorithm for ${\mathsf {LCR}}$ unless ${\mathsf {ETH}}$ fails. This indicates that the above algorithm is asymptotically optimal. Technically, we give a reduction from n-variable ${\mathsf {3}\text {-}\mathsf {SAT}}$ to ${\mathsf {LCR}}$ such that the size of the contributor in the constructed instance is $\mathcal {O}(n)$. Then a $2^{o(\texttt {C})}$-time algorithm for ${\mathsf {LCR}}$ yields a $2^{o(n)}$-time algorithm for ${\mathsf {3}\text {-}\mathsf {SAT}}$, a contradiction to ${\mathsf {ETH}}$.

With a similar reduction, one can cross-compose ${\mathsf {3}\text {-}\mathsf {SAT}}$ into ${\mathsf {LCR}(\texttt {C})}$. This shows that the problem does not admit a polynomial kernel. The precise constructions and proofs can be found in the full version [9].

Proposition 11

• (a) ${\mathsf {LCR}}$ cannot be solved in time $2^{o(\texttt {C})}$ unless ${\mathsf {ETH}}$ fails.

• (b) ${\mathsf {LCR}(\texttt {C})}$ does not admit a polynomial kernel unless ${\mathsf {NP}\subseteq \mathsf {co}\mathsf {NP}/ {\mathsf {poly}}}$.

4 Bounded-Stage Reachability

The bounded-stage reachability problem is a simultaneous reachability problem. It asks whether all threads of a program can reach an unsafe state when restricted to s-stage computations. These are computations where the write permission changes s times. The problem was first analyzed in [1] and shown to be ${\mathsf {NP}}$-complete for finite-state programs. We give matching upper and lower bounds in terms of fine-grained complexity and prove the absence of a polynomial kernel.

Let $\mathcal {A}= ( D , a^0, (P_i)_{i \in [1..\texttt {t}]})$ be a program. A stage is a computation in $\mathcal {A}$ where only one of the threads writes. The remaining threads are restricted to reading the memory. An s-stage computation is a computation that can be split into s parts, each of which forming a stage.

We focus on a parameterization of ${\mathsf {BSR}}$ by $\texttt {P}$, the maximum number of states of a thread, and $\texttt {t}$, the number of threads. Let it be denoted by ${\mathsf {BSR}(\texttt {P}, \texttt {t})}$. We prove that the parameterization is ${\mathsf {FPT}}$ and present a matching lower bound. The main result in this section is the absence of a polynomial kernel for ${\mathsf {BSR}(\texttt {P}, \texttt {t})}$. The result is technically involved and reveals hardness of the problem.

Parameterizations of ${\mathsf {BSR}}$ involving $\texttt {D}$ and s, the number of stages, are not interesting for fine-grained complexity theory. We can show that ${\mathsf {BSR}}$ is ${\mathsf {NP}}$-hard even for constant $\texttt {D}$ and s. This immediately rules out ${\mathsf {FPT}}$ algorithms in these parameters. For details, we refer to the full version of the paper [9].

Upper Bound. We show that ${\mathsf {BSR}(\texttt {P}, \texttt {t})}$ is fixed-parameter tractable. The idea is to reduce to reachability on a product automaton. The automaton stores the configurations, the current writer, and counts up to the number of stages s. To this end, it has $\mathcal {O}^*(\texttt {P}^{\texttt {t}})$ many states. Details can be found in the full version [9].

Proposition 12

${\mathsf {BSR}}$ can be solved in time $\mathcal {O}^*(\texttt {P}^{2 \texttt {t}})$.

Lower Bound. By a reduction from ${\mathsf {k \times k ~ Clique}}$, we show that a $2^{o(\texttt {t}\cdot \log (\texttt {P}))}$-time algorithm for ${\mathsf {BSR}}$ would contradict ${\mathsf {ETH}}$. The above algorithm is optimal.

Proposition 13

${\mathsf {BSR}}$ cannot be solved in time $2^{o(\texttt {t}\cdot \log (\texttt {P}))}$ unless ${\mathsf {ETH}}$ fails.

The reduction maps an instance of ${\mathsf {k \times k ~ Clique}}$ to an equivalent instance $(\mathcal {A}= ( D , a^0(P_i)_{i\in [1..\texttt {t}]}), C^f, s)$ of ${\mathsf {BSR}}$. Moreover, it keeps the parameters small. We have that $\texttt {P}= \mathcal {O}(k^2)$ and $\texttt {t}= \mathcal {O}(k)$. As a consequence, a $2^{o(\texttt {t}\cdot \log (\texttt {P}))}$-time algorithm for ${\mathsf {BSR}}$ would yield an algorithm for ${\mathsf {k \times k ~ Clique}}$ running in time $2^{o(k \cdot \log (k^2))} = 2^{o(k \cdot \log (k))}$. But this contradicts ${\mathsf {ETH}}$.

Proof

(Idea). For the reduction, let $V = [1..k] \times [1..k]$ be the vertices of G. We define $D = V \cup \lbrace a^0 \rbrace$ to be the domain of the memory. We want the threads to communicate on the vertices of G. For each row we introduce a reader thread $P_i$ that is responsible for storing a particular vertex of the row. We also add one writer, $P_{ch}$, that is used to steer the communication between the $P_i$. Our program $\mathcal {A}$ is given by $( D , a^0, ( (P_i)_{i \in [1..k]}, P_{ch} ))$.

Intuitively, the program proceeds in two phases. In the first phase, each $P_i$ non-deterministically chooses a vertex from the i-th row and stores it in its state space. This constitutes a clique candidate $(1,j_1), \dots , (k, j_k) \in V$. In the second phase, thread $P_{ch}$ starts to write a random vertex $(1,j_1')$ of the first row to the memory. The first thread $P_1$ reads $(1,j_1')$ from the memory and verifies that the read vertex is actually the one from the clique candidate. The computation in $P_1$ will deadlock if $j_1' \ne j_1$. The threads $P_i$ with $i \ne 1$ also read $(1,j_1')$ from the memory. They have to check whether there is an edge between the stored vertex $(i,j_i)$ and $(1,j_1')$. If this fails in some $P_i$, the computation in that thread will also deadlock. After this procedure, the writer $P_{ch}$ guesses a vertex $(2,j_2')$ and writes it to the memory. Now the verification steps repeat. After k repetitions of the procedure, we can ensure that the guessed clique candidate is indeed a clique. Note that the whole communication takes one stage. Details are given in [9].    $\square$

Absence of a Polynomial Kernel. We show that ${\mathsf {BSR}(\texttt {P}, \texttt {t})}$ does not admit a polynomial kernel. To this end, we cross-compose ${\mathsf {3}\text {-}\mathsf {SAT}}$ into ${\mathsf {BSR}(\texttt {P}, \texttt {t})}$.

Theorem 14

${\mathsf {BSR}(\texttt {P}, \texttt {t})}$ does not admit a poly. kernel unless ${\mathsf {NP}\subseteq \mathsf {co}\mathsf {NP}/ {\mathsf {poly}}}$.

In the present setting, coming up with a cross-composition is non-trivial. Both parameters, $\texttt {P}$ and $\texttt {t}$, are not allowed to depend polynomially on the number I of given ${\mathsf {3}\text {-}\mathsf {SAT}}$-instances. Hence, we cannot construct an NFA that distinguishes the I instances by branching into I different directions. This would cause a polynomial dependence of $\texttt {P}$ on I. Furthermore, it is not possible to construct an NFA for each instance as this would cause such a dependence of $\texttt {t}$ on I. To circumvent the problems, some deeper understanding of the model is needed.

Proof

(Idea). Let $\varphi _1, \dots , \varphi _I$ be given ${\mathsf {3}\text {-}\mathsf {SAT}}$-instances, where each two are equivalent under $\mathcal {R}$, the polynomial equivalence relation of Theorem 8. Then each $\varphi _\ell$ has m clauses and n variables $\lbrace x_1, \dots , x_n \rbrace$. We assume $\varphi _\ell = C^\ell _1 \wedge \dots \wedge C^\ell _m$.

In the program that we construct, the communication is based on 4-tuples of the form $(\ell , j, i, v)$. Intuitively, such a tuple transports the following information: The j-th clause in instance $\varphi _\ell$, $C^\ell _j$, can be satisfied by variable $x_i$ with valuation v. Hence, our data domain is $D = ([1..I] \times [1..m] \times [1..n] \times \lbrace 0,1 \rbrace ) \cup \lbrace a^0 \rbrace$.

For choosing and storing a valuation of the $x_i$, we introduce so-called variable threads $P_{x_1}, \dots , P_{x_n}$. In the beginning, each $P_{x_i}$ non-deterministically chooses a valuation for $x_i$ and stores it in its states.

We further introduce a writer $P_w$. During a computation, this thread guesses exactly m tuples $(\ell _1, 1, i_1, v_1), \dots , (\ell _m, m, i_m, v_m)$ in order to satisfy m clauses of potentially different instances. Each $(\ell _j, j, i_j, v_j)$ is written to the memory by $P_w$. All variable threads then start to read the tuple. If $P_{x_{i}}$ with $i \ne i_j$ reads it, then the thread will just move one state further since the suggested tuple does not affect the variable $x_i$. If $P_{x_i}$ with $i = i_j$ reads the tuple, the thread will only continue its computation if $v_j$ coincides with the value that $P_{x_i}$ guessed for $x_i$ and, moreover, $x_i$ with value $v_j$ satisfies clause $C^{\ell _j}_{j}$.

Now suppose the writer did exactly m steps while each variable thread did exactly $m+1$ steps. This proves the satisfiability of m clauses by the chosen valuation. But these clauses can be part of different instances: It is not ensured that the clauses were chosen from one formula $\varphi _\ell$. The major difficulty of the cross-composition lies in how to ensure exactly this.

We overcome the difficulty by introducing so-called bit checkers $P_b$, where $b \in [1..\log (I)]$. Each $P_b$ is responsible for the b-th bit of ${{\mathrm{\texttt {bin}}}}(\ell )$, the binary representation of $\ell$, where $\varphi _\ell$ is the instance we want to satisfy. When $P_w$ writes a tuple $(\ell _1, 1, i_1, v_1)$ for the first time, each $P_b$ reads it and stores either 0 or 1, according to the b-th bit of ${{\mathrm{\texttt {bin}}}}(\ell _1)$. After $P_w$ has written a second tuple $(\ell _2, 2, i_2, v_2)$, the bit checker $P_b$ tests whether the b-th bit of ${{\mathrm{\texttt {bin}}}}(\ell _1)$ and ${{\mathrm{\texttt {bin}}}}(\ell _2)$ coincide, otherwise it will deadlock. This will be repeated any time $P_w$ writes a new tuple to the memory.

Assume, the computation does not deadlock in any of the $P_b$. Then we can ensure that the b-th bit of ${{\mathrm{\texttt {bin}}}}(\ell _j)$ with $j \in [1..m]$ never changed during the computation. This means that ${{\mathrm{\texttt {bin}}}}(\ell _1) = \dots = {{\mathrm{\texttt {bin}}}}(\ell _m)$. Hence, the writer $P_w$ has chosen clauses of just one instance $\varphi _{\ell }$ and with the current valuation, it is possible to satisfy the formula. Since the parameters are bounded, $\texttt {P}\in \mathcal {O}(m)$ and $\texttt {t}\in \mathcal {O}(n + \log (I))$, the construction constitutes a proper cross-composition. For a formal construction and proof, we refer to the full version [9].    $\square$

5 Conclusion

We studied several parameterizations of ${\mathsf {LCR}}$ and ${\mathsf {BSR}}$, two safety verification problems for shared-memory concurrent programs. For ${\mathsf {LCR}}$, we identified the parameters $\texttt {D}$, $\texttt {L}$, and $\texttt {C}$. Our first algorithm showed that ${\mathsf {LCR}(\texttt {D}, \texttt {L})}$ is ${\mathsf {FPT}}$. Then, we used a modification of the algorithm to obtain a verification procedure valuable for practical instances. The main insight was that due to a factorization along strongly connected components, the impact of $\texttt {L}$ can be reduced to a polynomial factor in the time complexity. We also proved the absence of a polynomial kernel for ${\mathsf {LCR}(\texttt {D}, \texttt {L})}$ and presented a lower bound which is a root factor away from the upper bound. For ${\mathsf {LCR}(\texttt {C})}$ we gave a tight upper and lower bound.

The parameters of interest for ${\mathsf {BSR}}$ are $\texttt {P}$ and $\texttt {t}$. We have shown that ${\mathsf {BSR}(\texttt {P},\texttt {t})}$ is ${\mathsf {FPT}}$ and gave a matching lower bound. The main contribution was to prove it unlikely that a polynomial kernel exists for ${\mathsf {BSR}(\texttt {P}, \texttt {t})}$. The proof relies on a technically involved cross-composition that avoids a polynomial dependence of the parameters on the number of given ${\mathsf {3}\text {-}\mathsf {SAT}}$-instances.