1 Introduction

In the context of modern geostatistics, Monte Carlo Simulation (MCS) or simply simulation can be summarized by (1) the formulation of a problem with input variables, a transfer function and response variables, (2) the simulation of realizations of the input variables, (3) the application of the transfer function to compute the response variables of interest, and (4) the assembly of the simulated response variables into a probability distribution. The distribution of response variables can be used to understand uncertainty and, perhaps, for decision making.

The input variables could be the rock type and grade on a suitable grid, the transfer function could be the calculation of resources and the response variables could be the resources or reserves expressed as tonnages, grade and quantity of metal. A comprehensive simulation study could expand the input variables to include modeling parameters, price, costs and other economic and engineering parameters. The transfer function could be a model of the entire mine planning and economic forecasting process. The response variables could be key performance indicators such as net present value. The probability distributions of the input variables must be established prior to simulation; typically by a mathematical model such as the multivariate Gaussian model. The transfer function must be known to process realizations of the input variables to response variables of interest.

The key operation in simulation is the drawing of realizations from a specified probability distribution. This is done in a fair manner for unbiased results. Pseudorandom number generators generate numbers that have properties very close to random numbers, but are indexed to a seed. These numbers are uniform between 0 and 1, yet our input distributions are rarely uniform so the corresponding quantile is drawn from the distribution we are simulating from, z = F−1(r) where F(•) is the cumulative distribution, z is the simulated value and r is the random number.

Consider a simple example of three dice. The input variables are the three numbers showing on the faces of three fair cubic dice. The cumulative distribution of each input variable has six equal steps. The transfer function is the summation operator. The response is the sum. As illustrated on Fig. 7.1, one realization is generated by three random numbers, e.g., 0.69, 0.062 and 0.78 leading to a realization of 5, 1 and 5. Simulation is repeated for multiple realizations. The response distribution shown is the result for 100 realizations. There are many points that could be reinforced from this small example. The distribution of the input variables must be known prior to simulation; simulation is primarily transferring input variable uncertainty through a transfer function to response variable uncertainty. The space of uncertainty in this example is only 63 = 216, which is a very small number, but the space of uncertainty is practically infinite in geological modeling where there are many variables at many locations. Categorical variables require an arbitrary ordering. Finally, it would be wrong to focus on one realization; in this example we should not conclude that the first and third dice are likely high numbers and the second die is a low number. We only understand the result of simulation by considering an ensemble of realizations. This is a critical point.

Fig. 7.1
figure 1

Simulation of the outcome on three dice (left). Histogram of the sum of the outcomes on three dice (right). One hundred realizations are shown

Full size image

Although many theoreticians and practitioners understand this point, it is not emphasized enough. Most software is aimed at processing one block model at a time. Resources are often presented as a single value instead of a distribution.

There are many examples of experimental mathematics in history. The scientists on the Manhattan Project are credited with the formulation and popularization of Monte Carlo simulation (MCS) or simply simulation. There are interesting historical references and internet resources. The framework of transferring input uncertainty to response variable uncertainty is often referred to as simulation. Adjectives such as Monte Carlo, stochastic or conditional are sometimes added. The outcomes of simulating are called simulations or realizations.

The pioneers of simulation suspected where we would take the method. The closing paragraph in Hammersley and Handscomb (1964) is telling: Usually there are many nodes and possible paths, so many that a complete enumeration of the situation is impossible. This suggests a fruitful field for sampling and search procedures, but as yet little Monte Carlo work has been done here. There are challenging problems here for research into Monte Carlo techniques on multivariable problems. They knew we had to sample a reasonable set of realizations from the practically infinite space of uncertainty. They knew we would be challenged by multiple dependent variables. They did not know that 50 years later many practitioners would still struggle managing an ensemble of realizations.

This chapter is organized into five main sections supporting a case to use all realizations all the time. First, some principles of simulation are presented to set the context. Second, principles of decision making in presence of uncertainty are discussed to establish that earth scientists are not alone. Thirdly, some details of geostatistical simulation are presented to highlight important differences from simulation of independent variables. Fourthly, some details of resource decision making are presented to highlight important differences from the general principles including the information effect. Finally, some possible alternatives to using all realizations all the time are reviewed. A case is made to consider the correct approach, that is, consider all realizations all the time and base decisions on the appropriate expected value when required.

2 Simulation

In the early days of simulation there was a particular concern related to the pseudorandom numbers applied in the simulation. A large part of early texts on simulation is devoted to the generation of pseudorandom numbers. This concern has largely been addressed and there is little practical concern with the pseudorandom number generators used in most software.

Another concern is in replacing the reality with a numerical model. Many early applications of Monte Carlo simulation were directed at solving integration and other equations where the transfer function is a very close representation of the physical situation. Examples of well represented physical systems are the study of radiation shielding and reactor criticality. The simulation tracks simulated particles through collisions where the particles are absorbed, scattered or split according to physical principles. There were few concerns about this simulation due to the close correspondence between the numerical setup and the physical reality. Increasingly, complex non-linear systems are modeled with empirical statistical models causing more concern.

It is impossible to model the details of the natural geological processes that led to the deposit under study. Empirical statistical models are required. Geostatistical models do not represent the original depositional and diagenetic processes. Although all models are wrong (Box and Draper 1987) they can be useful if assembled carefully with established workflows and appropriate checking.

The premise of simulation is to construct many realizations that are equally likely to be drawn. Realizations and responses more probable than others will be drawn more often. A fundamental principle of simulation is to consider many realizations. One hundred realizations may not be enough. The average of the one hundred realizations on Fig. 7.1 was 9.6, yet the true expected response for that particular process is 10.5. This suggests that the number of realizations should be quite large. Indeed, early practitioners of simulation considered that thousands of realizations were required unless some form of stratified or directed sampling could be implemented. Of course, the problems considered early on were small compared to the complexity of modern geological modeling where 10s of variables at 10s of millions of locations are considered. In many cases, the professional and computational effort of generating more than 100s of realizations would be better spent improving the model. This claim is supported by two observations: (1) the variability at multiple locations partially cancels out, and (2) there is too much uncertainty in the model to expend resources on thousands of realizations.

Another fundamental principle of simulation is that all realizations are considered in downstream calculations. One application is to pass all realizations through the transfer function to construct a distribution of responses, for example, resource estimates. The realizations could be passed through a decision tree structure to help support a decision. Finally, the realizations could all be used in the optimization of decision variables. Incorrect or suboptimal decisions could be taken if too few realizations are considered.

The concept or ranking and choosing a few realizations is motivated by the large computational cost running realizations through a complex full physics transfer function. The processing the realizations through a simplified transfer function could rank the realizations and permit choosing a smaller number for the complex full physics transfer function. Decision making and optimization applied with one or a few realizations leads to over fitting to those realizations.

In some cases, the transfer function and decision variables are known. For example, calculating the recoverable reserves above a specified economic cutoff. In other cases, aspects of the decision must be optimized. For example, deciding the ultimate pit limits, choosing drill hole locations or deciding on the destination of mined material. If the transfer function and decision variables are known, then a probability distribution of each critical response variable is assembled from the realizations where the result of each realization is equally weighted. This distribution provides a direct understanding of uncertainty. There are many ways of summarizing the uncertainty. Considering the 0.1, 0.5 and 0.9 quantiles is common in petroleum applications, but considering the probability to be within 15% of expected is a reasonable measure of uncertainty.

If aspects of the decision are not finalized, then decision making and optimization must be considered before calculating a distribution of the critical response variables.

3 Decision Making

Decision making in presence of uncertainty has long been studied (Bernoulli 1954; Kochenderfer 2015). The general framework of decision making could be summarized by (1) define clearly stated objectives within a value system, that is, a measure of utility (often profit), (2) enumerate the alternative decisions that could be taken—perhaps in a decision tree, (3) compute the expected utility for all alternatives, and (4) choose the alternative that maximizes expected utility. This framework becomes confounded with large one-time decisions or significant unknown unknowns that defy straightforward quantification. Grade control and mine planning decisions are made repeatedly within a clear economic framework.

Consider a recently loaded truck. The expected profit of the material if the truck goes to the mill would be computed by the average over all realizations, say $6.75 per tonne. The expected profit if the material goes to the waste dump is the average of a similar calculation over all realizations, say −$2.00 per tonne. With no other information, the truck should be sent to the mill. There are complicating factors including sequencing, stockpiling, limited milling capacity, but the principle stands. Decisions should be based on expected values as late as possible.

Decisions are based on the average over all realizations and not on one particular realization. The realizations are simply a means to represent uncertainty. One realization should not be chosen for decision making because that would mean ignoring other equally likely possibilities; the expectation is the only way to resolve the ambiguity of multiple realizations. The decision is also made as late as possible. Calling a block of material in a long term resource model ore may be convenient as an interim decision for planning purposes, but this decision would certainly be revisited with production sampling at the time of grade control.

There is another aspect to taking the expected value as late as possible. The expected value is calculated with the last numbers considered: utility or profit. The expected value should not be taken earlier. The correct decision would not always be found if the grades were averaged and the decision based on the utility computed from the expected grade. Many calculations are non-linear and the utility computed on the average of realizations is not the average (expected) utility computed on the realizations.

The distributions of payoff/utility for each possible decision are evaluated to determine the best decision. Some decisions may be completely dominated by others, that is, the best possible payoff of a dominated decision is less than the worst payoff of an alternative. All dominated decisions should be rejected. Some decisions are stochastically dominated by others (Levy 2016). That is, each quantile on the payoff distribution is less than the same quantile on an alternative. Decision makers should also reject all stochastically dominated decisions. The expected utility would be considered when multiple decisions remain to establish the optimal one.

A challenge in many geological resource application problems is that the decision involves many different options. The precise sequence of extraction or the position of all production wells is combinatorial and all options cannot be considered. Optimization algorithms are implemented where the objective function is the appropriate expected value of profit or utility over all realizations. The distribution of uncertainty in utility is only known once optimization is complete.

The utility function quantifies our position on risk; however, it is not simple to establish the utility function in practice. One approach based on the idea of the efficient frontier could be considered (Francis, and Dongcheol 2013; Hanoch and Levy 1969). Decisions are optimized based on maximum expected profit and minimum risk. The ones that are not dominated are retained as the efficient frontier. Judgement could be used to evaluate the differences between these decisions and to choose a path forward.

4 Geostatistical Simulation

The simulation of mineral deposits has evolved significantly over the last twenty years. The simulation is often hierarchical and multivariate with unequally sampled data and parameter uncertainty. A variety of techniques are used to create realizations that reproduce all available data and represent the variability that may influence the planning and decision making process (Caers 2011; Chilès and Delfiner 2012).

The scope of this chapter is not to present details of geostatistical simulation (Deutsch and Journel 1998; Goovaerts 1997). The main steps in managing the results will be reviewed. The transfer functions of greatest interest are resources and reserves within reasonably large volumes, uncertainty versus data spacing, uncertainty and variability in mine planning and sometimes optimization of blending and other engineering designs. Parameter uncertainty is important for the resources within large volumes. Data uncertainty is important with unequally sampled variables (common with geometallurgical and geomechanical variables). The steps in geostatistical simulation could be divided into five unit operations.

  • Model Setup involves the formulation of the modeling workflow. A hierarchical modeling of the deposit limits, rock types and multiple grades is specified. The grid node spacing relative to production volumes of interest must be chosen. The model setup defines the software algorithms and input parameters for each step. The number of realizations is chosen at the start to ensure that there is one realization of parameters for each realization of data for each realization of the deposit. 100 or 200 realizations is common.

  • Parameter Uncertainty amounts to simulating realizations of all of the modeling parameters identified in the Model Setup including those for gross volume uncertainty, rock type proportion uncertainty, histogram uncertainty, variogram uncertainty and multivariate relationship uncertainty. The multivariate spatial bootstrap is widely used. The uncertainty in some global parameters may be specified by experience.

  • Data Uncertainty involves two main aspects. The first is sampling realizations of the available data if the uncertainty in the data is considered important. For example, there may be a 10% relative error in the data based on the data collection and processing. A spatial bootstrap could be considered to get the uncertainty in the mean error, then realizations of the data would be assembled. The second aspect, if required, is to fill missing data (data imputation) and downscale data with a larger support than the rest of the data (Barnett and Deutsch 2015).

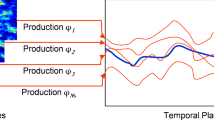
  • Simulate Realizations is the operation where deposit models of all variables are assembled. These would follow the steps identified in the Model Setup. There would be one realization for every data and parameter realization. These are constructed hierarchically and with the correct dependencies by rock-type and between all variables. These realizations have to be checked to the greatest extent possible. The process of conditioning the realizations will update the prior uncertainty quantified in the second step. A schematic illustration of the realizations is shown below.

  • Process in Transfer Function involves evaluating every realization for all calculations of interest. Local uncertainty can be computed for any block size. Resources can be computed for the entire deposit, within a mine plan or for different elevations. An ultimate pit could be computed for every realization. The economic performance of each realization could be evaluated. The uncertainty in each response variable is known non-parametrically through the distribution of responses. The expected response can be computed as an average of the responses.

The uncertainty is directly observed. It is common to assess sensitivity by indexing each realization by summary input parameters, for example, the gross rock volume, proportions of rock types, average grades, variogram ranges, and correlation coefficients. Then, the relationship between the input parameters and the response variables can be fit by a response surface and the sensitivity evaluated and presented by tornado charts. Further post processing is discussed below.

5 Resource Decision Making

All realizations should be used all the time. Anything that can be computed on one block model can be computed on one hundred, then the distribution of the response variable of interest can be assembled and summarized by expected value and other statistics. If a decision must be made, then the decision variable (economic value for ore, leach, dump…) can be computed on all realizations (Da Cruz 2000; Tversky and Kahneman 1992). The expected response determines the optimal decision.

When a mine plan is specified, then it is straightforward to evaluate all realizations through the plan and observe the uncertainty in key response variables due to the present state of incomplete knowledge. Sometimes the plan is not fixed and the realizations are to be used for planning and optimization. In principle this is not difficult. The objective function is the expected performance over all realizations. Some realizations may perform poorly with a particular plan and some better, but it is the expected value of the performance over all realizations that is the function to optimize (Pyrcz and Deutsch 2014). Considering the concept of the efficient frontier, the risk may be penalized to consider decisions that more reasonably suit the organizations position on risk.

Fixing a production plan and running multiple realizations through the plan can be somewhat pessimistic since this assumes the plan cannot change in the future. In fact, more data becomes available as mining proceeds and the plan can adapt to the new knowledge.

Additional drilling is done to improve delineation ahead of production (Damsleth et al. 1992). Production sampling improves short-term mine planning and leads to a better understanding of the deposit. Uncertainty will resolve itself as production takes place and the mineral deposit is exposed for our greater understanding. The life-of-mine plan is updated on a regular basis (often yearly). A base case long term plan can be established with the current uncertainty and different options explored. The value of future information could be determined by simulating the additional data; this was the idea of the Simulated Learning Model (Cuba et al. 2014). There is flexibility for the plan to adapt to the future, but not change the past.

Flexibility is reduced as mining takes place. There is value in future flexibility (Stirling 2012). A slightly poorer decision, based on currently expected performance, with greater future flexibility may be better than a slightly better decision with less flexibility. The simultaneous optimization over multiple realizations should consider this flexibility.

Optimizing over all realizations simultaneously and considering all realizations through all engineering designs is correct, but difficult for some practitioners to accept (Bratvold et al. 2003; Guyaguler and Horne 2001; Wang et al. 2012). The computational challenges are exaggerated. The computers now are more than 100 times faster than they were about 10 years ago. Also, the ability to use multiple cores and GPUs means that we do not need to compromise much on the complexity of our calculations to consider all realizations all the time. The attraction of a single numerical geological model is undeniable. Most software does not permit easy visualization of multiple realizations. Although the ensemble of realizations should be managed together, the non-uniqueness of multiple realizations is disturbing. The simplest alternative is to use a kriged model for planning and all reporting purposes; the simulated realizations are reserved for uncertainty statements and an understanding of variability.

6 Alternatives to All Realizations

Some simple summary models are useful. The probability to meet an economic threshold is useful; high probability is good. The local probability to exceed, say, the global 0.75 quantile is also useful to identify the areas that are surely high: if this probability is high (say over 0.9), then the area is surely high. The local probability to be below, say, the global 0.25 quantile is useful to identify areas that are surely low: if this probability is high (say over 0.9), then the area is surely low. The local variance or the probability to be within 15% of expected are also useful summary measures.

Another approach is to collapse uncertainty into a few summary measures and base planning on them. For example, multiple realizations could be summarized by proportions of ore and waste over multiple realizations within reasonable planning volumes. One could even consider that each block has a proportion of ore and a proportion of waste. The block will be found to be all ore or all waste in the future; the proportions are simply used to collapse uncertainty.

Summarizing multiple realizations is useful. The summaries make use of the multiple realizations. Plans optimized on a summary are never as good as plans optimized over all realizations simultaneously (primarily due to the complexity and non-linearity of most planning operations); however, it may be the only practical approach offered by the available software.

The realizations are equally probable; there is no right one and there is no P50 one and we have no idea if one is closer to the truth than the others. A dangerous practice emerged in the early days of simulation: run the realizations through a quick to calculate transfer function, rank the realizations by the quick-to-calculate response, then consider only selected realizations (say, the P10, P50 and P90) in the “real” more complicated transfer function.

In general, individual realizations should never be singled out for calculations. There is much about a single realization that depends on the random number generator and that is not real. Any one realization could be misleading. There are some specific calculations that could be done with one realization because the variability at specific locations (that we do not trust) averages out over multiple realizations. Blending studies and drilling spacing studies are two examples. It may be enough to run one or a few realizations through a simulation of the homogenization steps to understand the probability of plant upsets and undesirable circumstances. The variability at multiple locations reflects the overall variability and the specific location/time is not critical.

In almost all cases, the simplest and most robust approach is to consider all realizations and take expected values at the end to report a single result.

7 Concluding Remarks

Monte Carlo Simulation is a well-established experimental mathematical approach to transfer uncertainty in input geological and engineering variables through to response variables. The primary aim of this chapter was to point out the danger of using one realization instead of an ensemble of realizations. One realization may fall near the middle based on a quick-to-calculate response variable and yet it could be unusually high in some places and low in others. Planning on one realization could be misleading. The nonlinearity and complexity of many real response variables requires the ensemble of realizations to be considered for proper planning and uncertainty assessment. All realizations all the time – anything less will not give correct results.