1 Introduction

Images are unavoidably corrupted by noise during acquisition and transmission process. Therefore, image denoising has received increasingly attention in the past decades. In this paper, we focus on recovering an underlying image from an observation that has been corrupted by zero mean additive Gaussian noise, which can be formulated as:

$$\begin{aligned} f=s+n \end{aligned}$$

where f is the observation, s is the clean image, and n is independent additive noise.

State of the art methods in image denoising refer to variational method, wavelet frame based method and non-local (NL) mean method. Wavelet frame based method is started from [1, 2] for high resolution image reconstructions. The basic idea for this method is that image can be sparsely approximated by some wavelet frames. There are three forms to utilize the sparseness of the wavelet frame coefficients, namely analysis based approach, synthesis based approach and balanced based approach. These three approaches are developed independently. The detailed and integrated descriptions of the three approaches can be found in [3]. NL mean method is first introduced in [4] for image denoising and has recently surged in popularity to solve other inverse problems in image processing [5,6,7]. Its advantage is to relate many image pixels that may be far away in spatial domain.

One of the most successful variational methods is total variation (TV) based regularization, which is initially introduced in the work [8] by Rudin-Osher-Fatamin(ROF). ROF model is initially solved by partial differential equation (PDE), which has high computational complexity. Chambolle’s projection algorithm is one of the most efficient methods to solve the ROF model [9]. ROF model works well on cartoon type image regions, but does not perform well on textural regions. Separating homogeneous component from texture is very important technique to deal with such problem and has gained significant attention in the past years [10,11,12,13,14,15,16,17]. However, these methods fail to distinguish between texture and noise. Furthermore, the regularization parameters that relate to the denoising intensity in these models are global. It is impossible for a single parameter to give good performance for all regions at the same time.

Local variance is often used to separate texture and noise regions in natural image denoising. In [18,19,20,21], the authors use the local variance measure to distinguish between texture and noise under different frameworks. In this paper, we proposed a variational denoising model with local variance constraints imposed on the dyadic image regions. The underlying image denoising model partitions the image into fine scale non-overlapping dyadic regions and each region corresponds to a regularization parameter. Thus, the regularization parameter in the proposed model is now space adaptive and can be selected to make each local variance constraint hold.

2 The Proposed Method

Texture image denoising is a challenge task in image processing. It is mainly because of the vaguer definition of texture. Until now, there is no unified definition for texture. It is often represented as fine scale-details, usually with periodicity and oscillatory nature. Moreover, texture is highly dependent on image scale. It is almost impossible to separate texture from noise thoroughly for all types of images. Therefore, certain priori information is needed. The priori knowledge of the proposed model is that the local oscillating property of the noise component is much weaker than that of the texture.

TV based image denoising model is an efficient tool to decompose an image into cartoon part and oscillating part (texture and noise), but could not distinguish between texture and noise. Our motivation is based on the fact that if we extract clear textures from the oscillating part and add it to the cartoon part, the quality of the restored image will be much more better. Therefore, we will first introduce a variational model to extract clear textures from noisy data.

A popular constraints imposed on the noise component of the image in TV based denoising method is to satisfy the following demand:

$$\begin{aligned} \int _\varOmega (f(x)-I(x))^2dx=\sigma ^2 \end{aligned}$$
(1)

where \(\sigma \) is the noise standard deviation, f is the observed image and I is the restored one. This global constraint leads to a global regularization parameter which could not perform well on textural regions and cartoon regions simultaneously. In order to denoise adaptively on the different types of regions, we propose a denoising/decomposition model with local constraints on the dyadic regions of the image.

Let \(\gamma \) be an image containing only noise and texture. For instance, \(\gamma \) is the residual of the ROF model when the parameter is small. We are aimed to recover the texture as much as possible from the noisy data. We propose the following model:

$$\begin{aligned}&\min _v\quad \Vert \gamma -v\Vert _{L^2}^2 \nonumber \\&s.t. \quad \int _{Q_{J,k}}|v-m_{Q_{J,k}}(v)|^2dx=S_k |Q_{J,k}|,\quad \forall k\in \varGamma _j \end{aligned}$$
(2)

where v is the noise part, and therefor \(\gamma -v\) represents the texture. \(m_{Q_{J,k}}(v)\) denotes the mean value of v on dyadic region \(Q_{J,k}\), i.e., \(m_{Q_{J,k}}(v)=\frac{1}{|Q_{j,k}|}\int _{Q_{j,k}} v(x)dx\). Thus, the constraints in the model correspond to the assumption that the local variance of the noise is \(S_k\). \(S_k\ge 0\) is assumed to be given a-priori. In this model, we partition the image domain \(\varOmega \) into non-overlapping dyadic regions \(Q_{J,k}=\left[ \frac{k_1}{2^J},\frac{k_1+1}{2^J}\right] \times \left[ \frac{k_2}{2^J},\frac{k_2+1}{2^J}\right] \), where \(k=(k_1,k_2)\in \varGamma _J=\{0,1,\cdots ,2^J-1\}^2\).

The optimization problem (2) is equivalent to the following unconstraint optimization problem

$$\begin{aligned} \min \limits _{v}\left\{ \Vert \gamma -v\Vert _{L^2}^2+\sum _k\lambda _k \int _{Q_{j,k}}|v-m_{Q_{J,k}}(v)|^2dx\right\} \end{aligned}$$
(3)

where parameter \(\lambda _k\ge 0\) should be taken to make the constraints in (2) hold.

This problem can be written as a sum of independent problems

$$\begin{aligned} \min _v\left\{ E_k(v)=\int _{Q_{J,k}}(\gamma -v)^2dx+\lambda _k\int _{Q_{J,k}}|v-m_{Q_{J,k}}(v)|^2dx\right\} \end{aligned}$$
(4)

The energy function \(E_k(v)\) is quadratic, thus convex and reaches a unique minimum. Starting from the initial condition \(v_0=\gamma \), \(\lambda _k=\lambda _0\) for all \(k\in \varGamma _J\). we perform a gradient descent as follows:

$$\begin{aligned} v^{t+1}=v^t-\tau \nabla E_k \end{aligned}$$
(5)

where the derivative of the energy function with respect to v is

$$\begin{aligned} \nabla E_k=-2(\gamma -v)+2\lambda _k(v-m_{Q_{J,k}}(v)) \qquad x\in Q_{J,k} \end{aligned}$$
(6)

When the energy reaches its minimum, we have

$$\begin{aligned} -(\gamma -v)+\lambda _k(v-m_{Q_{J,k}}(v))=0 \qquad x\in Q_{J,k} \end{aligned}$$
(7)

In order to enforce the constraint in model (2), we multiply the Eq. (7) by \(v(x)-m_{Q_{J,k}}(v)\) and integrate over \(Q_{J,k}\). Then we can get

$$\begin{aligned} \lambda _k\int _{Q_{J,k}}|v-m_{Q_{J,k}}(v)|^2dx-\int _{Q_{J,k}}(\gamma -v)(v-m_{Q_{J,k}}(v))dx=0 \end{aligned}$$
(8)

Knowing that\(\int _{Q_{J,k}}|v-m_{Q_{J,k}}(v)|^2dx=S_k |Q_{J,k}|\), \(\lambda _k\) can be updated by

$$\begin{aligned} \lambda _k=\frac{\int _{Q_{J,k}}(\gamma -v)(v-m_{Q_{J,k}}(v))dx}{S_k |Q_{J,k}|} \end{aligned}$$
(9)

Once \(\lambda _k\) is updated, we restart the minimization process with the new value of \(\lambda _k\) until convergence. Therefore, the algorithm to solve the problem (2) can be described as follows:

  1. 1.

    choose initial condition \(v_0=\gamma \), \(\lambda _k=\lambda _0\) for all \(k\in \varGamma _j\).

  2. 2.

    perform \(v^{t+1}=v^t-\tau \nabla E_k\) for all k and get the minimum \(v_k^*\).

  3. 3.

    update \(\lambda _k\) by

    $$\lambda _k=\frac{\int _{Q_{J,k}}(\gamma -v_k^*)(v_k^*-m_{Q_{J,k}}(v_k^*))dx}{S_k |Q_{J,k}|}$$
  4. 4.

    restart 2 and 3 until \(\lambda _k\) don’t change significantly. Then the solution of model (2) is \(v=\sum \limits _k v_k^*\chi _{Q_{J,k}}(x)\).

Combining the model (2) and the state of the art methods, we propose the following hybrid image denoising scheme:

  1. 1.

    Apply one of image denoising methods (eg. TV method, NL mean method or wavelet frame based method) on the observation and obtain the restored image and the residual.

  2. 2.

    Apply the model (2) to the residual obtained by step (1) and get the noise part and texture part.

  3. 3.

    Add the texture part to the restored image in (1) and then get the final restored image.

3 Experimental Validation

In this section, we present various numerical experiments to validate our method. Simulation work is done through Matlab platform.

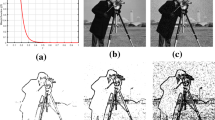
Figure 1 shows the testing image Barbara and its noisy version, with size of \(256\times 256\). The noise added is the zero-mean Gaussian noise with standard deviation \(\sigma =10\). Figure 2 shows the comparison of the restored results by the state of the art methods and their corresponding hybrid versions. From the comparison, one can easily see that the restored images by the hybrid methods contain more small details.

Fig. 1.
figure 1

Testing image “Barbara”: (a) original image; (b) noisy image.

Full size image
Fig. 2.
figure 2

The restored image by: (a) TV method; (b) TV based hybrid method; (c) NL mean method; (d) NL mean based hybrid method; (e) wavelet frame method (synthesis based approach); (f) wavelet frame based hybrid method.

Full size image
Fig. 3.
figure 3

Decomposition results by model (2): (a) residual by the TV method;(b) texture part of (a); (c) noise part of (a); (d) residual by the NL mean method; (e) texture part of (d); (f) noise part of (d); (g) residual by the wavelet frame based method; (h) texture part of (g); (i) noise part of (g).

Full size image
Fig. 4.
figure 4

Testing image “Baboon”: (a) original image;(b) noisy image.

Full size image

Figure 3 shows the decomposition result by model (2). One can see that some clear texture are extracted from the noisy data. Especially for the residual by the wavelet frame based method, the texture and noise are better distinguished by our model. This is because the residual obtained by the wavelet frame based method is more sparse.

Another testing image Baboon and its noisy version are shown in Fig. 4. The noise added is the zero-mean Gaussian noise with \(\sigma =15\). The comparison of restoration result by different methods is shown in Fig. 5. It is easy to see that the hybrid scheme can preserve more fine scale details. NL mean method performs very well for the image “Barbara”, for the reason that the self-recursive property is strong on this image which results in good matched patches in nonlocal method. However, for the images which has week self-recursive property, NL mean method often discards some small details of the image. For example, from the smaller tagged region of Fig. 5(b), we can see that the small white region in the corner of the eye would be barely visible, while from Fig. 5(e) this small detail is well preserved.

Fig. 5.
figure 5

Restored image by: (a) TV method; (b) NL mean method; (c) wavelet frame based method; (d) TV based hybrid method; (e) NL mean based hybrid method; (f) wavelet frame based hybrid method.

Full size image
Table 1. Comparison of PSNR by four methods for different images.
Full size table

The proposed method is compared in terms of peak signal to noise ratio (PSNR) with TV based method, NL mean method and wavelet frame method (synthesis based approach) in Table 1. The advantage of the hybrid methods in terms of PSNR is also consistent with the improvement of the visual quality.

4 Conclusion

In this paper, we have proposed a variational model to extract clear texture from noisy image data. The advantage of proposed model is that it considers the local oscillating properties of the texture and noise, and the Lagrange multipliers which control the denoising extent are spatial adaptive. For the image region with low local oscillating property (dominated by noise), the correspond Lagrange multiplier is small to enhance the denoising extent. For the image region with high local oscillating property (dominated by texture), the correspond Lagrange multiplier is large to preserve textures. Thus, much texture can be extracted from the noisy data and the texture is very clear and mixed with very little or no noise.