The Emerging Paradigm of Pebble Accretion

Abstract

Pebble accretion is the mechanism in which small particles (“pebbles”) accrete onto big bodies (planetesimals or planetary embryos) in gas-rich environments. In pebble accretion , accretion occurs by settling and depends only on the mass of the gravitating body , not its radius. I give the conditions under which pebble accretion operates and show that the collisional cross section can become much larger than in the gas-free, ballistic, limit. In particular, pebble accretion requires the pre-existence of a massive planetesimal seed. When pebbles experience strong orbital decay by drift motions or are stirred by turbulence, the accretion efficiency is low and a great number of pebbles are needed to form Earth-mass cores. Pebble accretion is in many ways a more natural and versatile process than the classical, planetesimal-driven paradigm, opening up avenues to understand planet formation in solar and exoplanetary systems.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

7.1 Introduction

The goal of this chapter is to present a physically motivated understanding of pebble accretion , elucidating the role of the disk, planet, and pebble properties, and to present the conditions for which pebble accretion becomes a viable mechanism to form planets. In this work, I discuss pebble accretion from a local perspective—a planet situated at some distance from its star—and do not solve for the more formidable global problem (planet migration or the evolution of the pebble disk ). However, clear conclusions can already be obtained from the local approach.

The plan of this chapter is as follows. In Sect. 7.1 I outline what is understood by pebble accretion . In Sect. 7.2 order-of-magnitude expressions for pebble accretion are derived, which are applied in Sect. 7.3 to address the question under which conditions pebble accretion is a viable mechanism. Section 7.4 highlights some applications.

7.1.1 What Is Pebble Accretion (Not)?

Pebble accretion is a planet formation concept that concerns the accretion of small particles (pebbles) of negligible gravitational mass onto large, gravitating bodies : planetesimals, protoplanets, or planets.¹ In a more narrow sense, pebble accretion is an accretion process where (gas) drag and gravity play major roles. Simply put, this means that the pebble has to be aerodynamically small and the planet to be gravitationally large.

Fig. 7.1

Examples of planet-pebble interactions, viewed in the frame co-moving with the planet. In each panel the filled circle denotes the physical size of the planet and the dashed circle its Hill sphere. Pebbles, characterized by a dimensionless stopping time τ _s , enter from the top, because of the sub-Keplerian motion of the gas (Sect. 7.1.2). The planet mass is given in terms of M _t [Eq. (7.10)]. Trajectories in red accrete. Only (c) and (d) qualify as pebble accretion, while (a), (b), and (e) fall in the ballistic regime. In (f) particles are so small (τ _s = 10⁻⁶) that they follow gas streamlines

Examples of particle-planet encounters best illustrate the concept. In Fig. 7.1 several encounters are plotted for pebbles of aerodynamical size τ _s and planet mass $\mathcal{M}_{\mathrm{pl}}$, which are dimensionless quantities (their formal definition is given later in Sects. 7.1.2 and 7.2.2, respectively). In (a) the small gravitational mass hardly perturbs the pebble trajectory . Consequently, the collisional cross section is similar to the geometric cross section, πR _pl ², where R _pl is the radius of the gravitating body . In (b), where the planetesimal mass corresponds to a body of radius R _pl ≈ 100 km, gravitational effects become more significant. Trajectories focus, resulting in a cross section larger than geometrical. The hyperbolic shape of the close encounters (see inset) strongly resembles those of the well-known planet-planetesimal encounters (Safronov 1969; Wetherill 1980). Similarly, in Fig. 7.1b gas-drag close to the body is of little importance, because the encounters proceed fast. However, on longer times gas drag does re-align the pebble with the gas flow.

In Fig. 7.1c, where the mass of the gravitating body is increased by merely a factor ten, the situation differs qualitatively from (b). First, the collisional cross section has increased enormously: it already is a good fraction of the Hill sphere. Second, the way how the pebbles are accreted is very different from (b). Pebbles often revolve the planet several times, before finally accreting (see inset). Indeed, where in (a) and (b) accretion relies on the physical size of the gravitating body, this is no longer the case in (c). Even when the physical radius would shrink to zero (i.e., a true point particle) the collisional cross section would be exactly the same, because pebbles simply settle down the potential well. Therefore:

Pebble accretion is characterized by settling of particles down the gravitational well of the planet. Pebble accretion only depends on the mass of the gravitating body, not its radius. It is further characterized by the absence of close, collisionless, encounters.

7.1.2 Aerodynamically Small and Large

Only particles tightly coupled to the gas qualify for pebble accretion. The level of coupling of a particle to the gas is customarily expressed in terms of the stopping time :

$$\displaystyle{ t_{\mathrm{stop}} = \frac{mv} {F_{D}}, }$$

(7.1)

where m the mass of the particle, v its relative velocity with the gas, and F _D the gas drag law. The stopping time is simply the time needed for gas drag to align the motion of the particle to that of the gas. For example, a particle falling in a gravitational field g will attain its equilibrium (settling) velocity after a time t _stop at which point g = F _D ∕m or v _settl (the settling velocity ) v _settl = gt _stop. In general, F _D depends on velocity in a non-trivial way, but for pebble-size particles under disk conditions we typically have that F _D is linear in v. This makes t _stop a function of the physical properties of the pebble (its size s and internal density ρ _•) and that of the gas, but independent of velocity. For example, in the Epstein regime we simply have t _stop = ρ _• s∕v _th ρ _gas where v _th is the mean thermal velocity of the gas and ρ _gas the gas density . A natural definition of “aerodynamical small” is that the stopping time is small in comparison to the inverse orbital frequency, Ω _K ⁻¹ or τ _s = Ω _K t _stop < 1. “Heavy” bodies have τ _s ≫ 1 and move on Kepler orbits. For them t _stop is the time needed to damp their eccentric motions.

Formally, the steady-state solution to the equations of motions for a particle of arbitrary τ _s , accounting for gas drag and pressure forces, read (Whipple 1972; Weidenschilling 1977a; Nakagawa et al. 1986):

$$\displaystyle\begin{array}{rcl} v_{r}& =& -\frac{2v_{\mathrm{hw}}\tau _{s}} {1 +\tau _{ s}^{2}} \equiv -v_{\mathrm{drift}},{}\end{array}$$

(7.2)

$$\displaystyle\begin{array}{rcl} v_{\phi }& =& v_{K} - \frac{v_{\mathrm{hw}}} {1 +\tau _{ s}^{2}},{}\end{array}$$

(7.3)

where v _r is the radial motion, v _ϕ the azimuthal, v _K the Keplerian velocity and v _hw, the disk headwind, the velocity offset between the gas and the Keplerian motion. Rotation is slower than Keplerian because the disk is partially pressure-supported:

$$\displaystyle\begin{array}{rcl} v_{\mathrm{hw}}& =& -\frac{1} {2}(h_{\mathrm{gas}}/r)^{2}v_{ K}\nabla _{\mathrm{log}}P,{}\end{array}$$

(7.4)

$$\displaystyle\begin{array}{rcl} & =& 54\,\mathrm{m\,s^{-1}}\: \frac{T_{1}} {300\,\mathrm{K}}\left ( \frac{\mu } {2.34}\right )^{-1}\left ( \frac{M_{\star }} {M_{\odot }}\right )^{-1/2}\frac{(-\nabla _{\mathrm{log}}P)} {3} \left ( \frac{r} {\mathrm{AU}}\right )^{(1/2-q)},{}\end{array}$$

(7.5)

where h _gas is the gas scale height, ∇_log P = ∂logP∕∂logr the logarithmic pressure gradient , μ the mean molecular weight, T ₁ the temperature at 1 au, and q the corresponding power-law index (as in T ∝ r ^−q). Because in many disk models q ≈ 1∕2 e.g., as obtained from a passively irradiated disk (Chiang and Goldreich 1997), we obtain that v _hw is a disk constant. For pebble accretion, the value of v _hw and its (possible) spatial and temporal variations are key parameters.

From Eq. (7.3) it follows that large bodies (τ _s ≫ 1) move on circular orbits (v _r = 0 and v _ϕ = v _K ) whereas small particles (τ _s < 1), moving with the gas, have their azimuthal velocities reduced by v _hw with respect to the Keplerian motion. The large body hence overtakes these particles. From its perspective, the particles arrive from the front at velocities ≈ v _hw.

7.1.2.1 Pebbles

In this chapter, I consider any particle of τ _s < 1 aerodynamically small. An (imprecise) lower limit may be added to the definition to distinguish drifting pebbles from “inert” dust. Usually, our definition of “pebble” then refers to particles of $10^{-3\ldots -2} \leq \tau _{s}\lesssim 1$. From Eq. (7.2), it is clear that these particles (indeed all particles around τ _s ∼ 1) have significant radial drift motions (This explains the slant seen in the incoming particle flow of the τ = 0. 1 pebbles of Fig. 7.1). It also implies that pebbles are constantly replenished: they are lost to the inner disk, but drift in from the outer disk. Pebble accretion, in contrast to planetesimal accretion, is therefore a global phenomenon: one has to consider the evolution of the dust population throughout the entire disk (Birnstiel et al. 2010; Okuzumi et al. 2012; Testi et al. 2014).

7.1.2.2 Planets

In our context a “planet” is any body with τ _s ≫ 1 moving on a circular orbit, large enough for gravity to become important.

7.1.3 The Case for Pebble Accretion

The case for pebble accretion can be made either from an observational or theoretical perspective. Observationally, pebbles are the particles inferred to be responsible for the emission seen at radio wavelengths in young disks. The argument is that the thermal emission is optically thin and is therefore proportional to the opacity of the emitting material, κ—a property of the dust grains . For a reasonable estimate of the temperature, the ratio in flux density at two wavelengths—the spectral energy index—translates into a ratio in opacity. Knowing the opacity in turn constrains the size of the emitting grains (or the maximum grain size if one considers a distribution). For example, particles much larger than the wavelength κ(λ) can be expected to be wavelength independent (grey absorption), whereas for small grains emission at wavelengths much longer than their size is suppressed (Rayleigh regime ). The observed spectral index translates into a size of the grains that carry most of the mass. Typically, mm- to cm-particles emerge from this spectral index analysis (e.g. Natta et al. 2007; Pérez et al. 2015). Another indication for the presence of pebble-size (drifting) particles is that disks are found to be more compact in the continuum than in the gas (Andrews et al. 2012; Panić et al. 2009; Cleeves et al. 2016).

The inferred pebble size also depends on their composition and internal structure (filling factor) of the particles; porous aggregates will result in a larger size (Ormel et al. 2007; Okuzumi et al. 2009). Even greater are the uncertainties in the total amount of mass in pebbles, because that depends on the absolute values of the opacity and on the assumption that the emitting dust is optically thin . A number of assumptions enter the calculation of the opacity; apart from the size, κ can also be affected by porosity (Kataoka et al. 2014), composition, and perhaps temperature (Boudet et al. 2005). (It is somewhat worrying that these systematic uncertainties are rarely highlighted in studies that quote disk masses ). Nevertheless, a large amount of pebbles are inferred in this way—ranging from 10² to possibly up to 10³ Earth masses (Ricci et al. 2010b,a; Andrews et al. 2013; Pérez et al. 2015). At these levels, it is hard to imagine that planetesimals (which cannot be directly observed) would yet dominate the solid mass budget. Therefore, from an observational perspective, it can well be argued that pebbles are planets’ primary building blocks.

Theoretically, the case for pebble accretion arises from the drawbacks of the classical, planetesimal-driven, model. In the inner disk growth is severely restricted because of the low isolation mass M _iso,clas [see, e.g., Lissauer 1987; Kokubo and Ida 2000 and Eq. (7.18)], which limits the mass of the planetary embryos to that of Mars.² In the outer disk M _iso,clas is sufficiently large, but here the problem is that growth is slow. First, planetesimal-driven accretion requires extremely quiescent disk to trigger runaway growth, which is already doubtful in case of moderate turbulent excitation (Nelson and Gressel 2010; Ormel and Okuzumi 2013). The second, more fundamental, problem is that planetesimal-driven growth suffers from negative feedback: a larger embryo entails a more excited planetesimal population, increasing the relative velocities of the encounters and suppressing the gravitationally focused collisional cross sections (e.g. Kokubo and Ida 2002). Unless the disk is unusually massive, this quickly suppresses embryo growth beyond ∼ 5 AU. It has been argued that collisional fragmentation would help to suppress eccentricities (and inclinations), either by gas or collisional damping (Wetherill and Stewart 1989; Goldreich et al. 2004; Fortier et al. 2013). However, a planet will carve a gap in a disk of low-e particles (i.e., when τ _s > 1 and e ≈ 0), preventing efficient accretion of planetesimals (Levison et al. 2010). Particle gaps may be avoided for aerodynamically smaller fragments, but then one really needs to address the orbital decay of this material (Kobayashi et al. 2011). In any case, when strong collisional diminution in the presence of gas has ground down planetesimals to particles of τ _s < 1, encounters enter the pebble accretion regime (Chambers 2014).

7.1.4 Misconceptions About Pebble Accretion

In closing, I list a number of misconceptions about pebble accretion:

• 1. Pebble accretion involves pebbles. Geologists define pebbles as particles of diameter between 2 and 64 mm (e.g. Williams et al. 2006). Our definition of pebble is aerodynamical: particles of stopping time below τ _s = 1. Therefore, in gas-rich environments, pebble accretion can take place over a very wide spectrum of particle sizes : from meter-size boulders to micron-size dust grain . Conversely, accretion of millimeter-size particles in a gas-free medium does not qualify as pebble accretion.

• 2. Pebble accretion is a planetesimal formation mechanism . Pebble accretion describes the process of accreting small particles on a gravitating body, e.g. a (big) planetesimal. How planetesimals themselves form is a different topic. Recent popular models hypothesize that planetesimals could form from a population of pebble-sized particles (Youdin and Goodman 2005; Johansen et al. 2007; Cuzzi et al. 2008). Planetesimal formation and pebble accretion can therefore operate sequentially. In that case, the key question is whether, say, streaming instability produces planetesimals large enough to trigger pebble accretion.

• 3. Pebble accretion is inevitable. It is sometimes alleged that the mere presence of a large reservoir of pebble-sized particles is sufficient to trigger pebble accretion. This is not the case. For pebble accretion, a sufficiently massive seed is needed as otherwise encounters will not fall in the settling regime . Formally, pebble accretion must satisfy the settling condition (see Sect. 7.2.1).

• 4. Pebble accretion is fast. It is true that pebble accretion is characterized by large collisional cross sections (Fig. 7.1c, d). However, the radial orbital decay of pebbles potentially renders the process inefficient: most pebbles simply cross the planet’s orbit, without experiencing any interaction. Therefore, pebble accretion depends on the pebble mass flux and, in particular, on how many pebbles are globally available. The low efficiency problem is especially severe when pebbles do not reside in a thin layer, i.e., for turbulent disks.

7.2 The Physics of Pebble Accretion

In this section I outline the key requirements for pebble accretion and derive order of magnitude expressions for pebble accretion rates based on timescales analysis. These expressions are, within orders of unity, consistent with recent works (Ormel and Klahr 2010; Ormel and Kobayashi 2012; Lambrechts and Johansen 2012, 2014; Guillot et al. 2014; Ida et al. 2016).

Fig. 7.2

Sketch of the pebble-planet interaction, viewed in the frame of the circularly moving planet (center). Pebbles, characterized by their aerodynamical size or stopping time, t _stop, approach a planet of gravitational mass GM _pl at impact parameter b. The relative velocity, v _∞ , is given by a combination of the disk headwind, v _hw, and the Keplerian shear. The unperturbed trajectory is indicated by the dashed line. Key timescales are the duration of the encounter, t _enc = 2b∕v _∞ , the settling timescale, t _settl = b∕v _settl, where v _settl is the sedimentation velocity evaluated at closest approach, and the stopping time, t _stop, of the pebble

7.2.1 Requirements and Key Expressions

An intuitive understanding of pebble accretion can be obtained from the timescales involved in an encounter between a gravitating body (planetesimal, planet) and a test particle . These are (see Fig. 7.2):

• The encounter time t _enc. The duration of the encounter or the time over which the particle experiences most of the gravitational force . It is given by t _enc = 2b∕v _∞ , where v _∞ is the (unperturbed) velocity at impact parameter b.

• The settling time t _settl. The time needed for a particle to sediment to the planet. The settling time is evaluated at the minimum distance b of the unperturbed encounter. There, the settling velocity reads v _settl = g _pl t _stop where the planet acceleration g _pl is evaluated at b. Hence t _settl = b∕v _settl = b ³∕GM _pl t _stop.

• The stopping time, t _stop. The aerodynamical size of the pebble.

Settling Condition The interaction will operate in the settling regime when:

• 1. The encounter is long enough for particles to couple to the gas during the encounter t _stop < t _enc; and

• 2. The encounter is long enough for particles to settle to the planet, t _settl < t _enc.

These conditions can also be combined into t _stop + t _settl < t _enc.

When either of the above does not materialize, there are no settling encounters and (according to our definition) there is no pebble accretion. The first condition expresses that gas drag matters during the interaction, which is where pebble accretion differs from planetesimal accretion. The second condition tells whether pebbles can actually sediment to the planet.

It is clear that a massive planet promotes settling, since the second condition becomes easier to fulfill and the first condition works better at larger b in any case. However, regarding the particle size the conditions work against each other. Very small particles (small t _stop) are always well coupled to the gas (condition 1), yet it can take them too long to settle (condition 2), unless b is small. On the other hand, large particles (large t _stop) satisfy the second condition at larger impact parameter, but they may nevertheless not qualify as “settling,” because they fail to meet condition 1.

7.2.2 Pebble Accretion Regimes

In order to derive the pebble accretion rates , the following strategy is employed. First, by equating t _settl and t _enc the largest impact parameter (b _col) is found that obeys condition 2. Then, a posteriori, it is verified whether b _col also satisfies condition 1.

The relative velocity v _∞ between pebble and planet follows from the headwind and the Keplerian shear :

$$\displaystyle{ v_{\infty }\simeq v_{\mathrm{hw}} + \frac{3} {2}\varOmega _{K}b. }$$

(7.6)

Therefore, an impact parameter of $b \sim \frac{2} {3}v_{\mathrm{hw}}/\varOmega _{K}$ divides two velocity regimes :

• The shear regime , valid at large b;

• The wind regime , valid when impact parameters are small.

These regimes are referred to as “Hill” and “Bondi,” respectively, by Lambrechts and Johansen (2012). Note that in the shear regime encounters last a dynamical timescale , t _enc ∼ Ω _K ⁻¹, meaning that particles τ _s < 1 satisfy condition 1.

7.2.2.1 Shear (Hill) Limit

Equating t _enc = Ω _K ⁻¹ with the settling timescale , we obtain

$$\displaystyle{ b_{\mathrm{sh}} \sim \left (\frac{GM_{\mathrm{pl}}t_{\mathrm{stop}}} {\varOmega _{K}} \right )^{1/3} \sim \tau _{ s}^{1/3}R_{\mathrm{ Hill}}\qquad (M_{\mathrm{pl}}\gtrsim M_{\mathrm{hw/sh}}), }$$

(7.7)

where R _Hill is the Hill radius. For τ _s ∼ 1 particles the impact parameter is comparable to the Hill radius, greatly exceeding the gas free limit [see Fig. 7.1e and Eq. (7.15)]. For τ _s < 1 impact cross sections decrease but not by much; particles down to τ _s = 0. 01 still accrete at impact parameter ≈ 20% of the Hill radius.

7.2.2.2 Headwind (Bondi) Limit

In the headwind limit, t _enc = 2b∕v _hw = t _settl gives

$$\displaystyle{ b_{\mathrm{hw}} \sim \sqrt{\frac{2GM_{\mathrm{pl } } t_{\mathrm{stop } } } {v_{\mathrm{hw}}}} \qquad (M_{{\ast}}\lesssim M_{\mathrm{pl}}\lesssim M_{\mathrm{hw/sh}}). }$$

(7.8)

The impact parameter increases as the square root of the stopping time and the planet mass , more steeply than in the shear limit . The transition from the headwind (valid for small t _stop or M _pl) to the shear limit occurs at the mass M _hw∕sh where b _hw = b _sh:

$$\displaystyle{ M_{\mathrm{hw/sh}} = \frac{v_{\mathrm{hw}}^{3}} {8G\varOmega _{K}^{2}t_{\mathrm{stop}}} = \frac{1} {8} \frac{M_{t}} {\tau _{s}}, }$$

(7.9)

where

$$\displaystyle{ M_{t} = \frac{v_{\mathrm{hw}}^{3}} {G\varOmega _{K}} = 1.6 \times 10^{-3}\,M_{ \oplus }\:\left ( \frac{v_{\mathrm{hw}}} {50\,\text{m s}^{-1}}\right )^{3}\left ( \frac{M_{\star }} {M_{\odot }}\right )^{-1/2}\left ( \frac{r} {\mathrm{AU}}\right )^{3/2} }$$

(7.10)

is a fiducial mass that measures the relative importance of headwind vs shear. Note that M _t is larger in the outer disk.

The headwind regime applies for M _pl ≤ M _hw∕sh. In addition, condition 1 also curtails the validity of the headwind regime. Equating t _enc = 2b _hw∕v _hw with t _stop it follows that pebble accretion shuts off for M _pl < M _∗ where

$$\displaystyle{ M_{{\ast}} = \frac{v_{\mathrm{hw}}^{3}t_{\mathrm{stop}}} {8G} = \frac{1} {8}M_{t}\tau _{s}. }$$

(7.11)

Interactions where M _pl < M _∗ follow ballistic trajectories, where accretion relies on hitting the surface of the planet (Fig. 7.1b). In that case the impact parameter can be obtained from the usual Safronov-type gravitational focusing with v _hw for the relative velocity , b _Saf ≃ R _pl v _esc∕v _hw where $v_{\mathrm{esc}} = \sqrt{2GM_{\mathrm{pl } } /R_{\mathrm{pl }}}$ is the surface escape velocity of the planet and R _pl its radius.

7.2.2.3 Aerodynamic Deflection

When the gravitational mass of the planetesimal becomes small (v _esc < v _hw) a natural minimum impact parameter is the physical radius R _pl. However, very small particles, very tightly coupled to the gas, will follow gas streamlines, avoiding accretion (Sekiya and Takeda 2003; Sellentin et al. 2013). This is referred to as aerodynamic deflection and is well known in the literature of, e.g., atmospheric sciences (Slinn 1976). It reduces the collisional cross section below the geometrical limit. The importance of aerodynamic deflection is quantified by the Stokes number³ Stk = v _hw t _stop∕R _pl. Particles of Stk ≪ 1 avoid accretion as they react to the gas flow on times (t _stop) smaller than the crossing time of the planetesimal t _enc ∼ R _pl∕v _hw.

However for gravitating bodies there is always a channel to accrete particles by settling, because the large t _enc—a lower limit to t _enc is always ∼ R _pl∕v _hw—enables the settling condition. To zeroth order, Eq. (7.8) still applies, even in cases where b _hw ≪ R _pl. A more detailed analysis should account for the modification of the flow pattern in the vicinity of the gravitating body, which depends on the Reynolds number (Johansen et al. 2015; Visser and Ormel 2016).

7.2.3 The Accretion Rate

In both the headwind and the shear regimes , the accretion rate $\dot{M} =\pi b^{2}v_{\infty }\rho _{P}$, is:

$$\displaystyle{ \dot{M}_{\mathrm{3D}} \sim 2\pi GM_{\mathrm{pl}}t_{\mathrm{stop}}\rho _{P} = 6\pi R_{\mathrm{Hill}}^{3}\tau _{ s}\varOmega _{K}\rho _{P} }$$

(7.12)

(as immediately follows from equating t _settl = t _enc and solving for b ² v _∞ ) where ρ _P is the density in pebbles. There is no transition between the shear and headwind regimes in terms of the accretion rate. However, Eq. (7.12) did assume that the pebbles are spread out in a thick disk; the accretion is 3D. When the pebbles reside in a thin layer, the accretion becomes rather:

$$\displaystyle{ \dot{M}_{\mathrm{2D}} \sim 2v_{\infty }b_{\mathrm{PA}}\varSigma _{P} = \left \{\begin{array}{ll} \sqrt{8GM_{\mathrm{pl } } t_{\mathrm{stop } } v_{\mathrm{hw }}}\varSigma _{P}&\quad \text{headwind reg.} \\ 2R_{\mathrm{Hill}}^{2}\varOmega _{K}\tau _{s}^{2/3}\varSigma _{P} &\quad \text{shear reg.} \end{array} \right. }$$

(7.13)

where Σ _P is the surface density in pebbles. It is instructive to contrast these rates with the classical expressions for Safronov focusing

$$\displaystyle{ \dot{M}_{\mathrm{Saf}} =\pi \left (\frac{v_{\mathrm{esc}}} {v_{\mathrm{hw}}}\right )^{2}R_{\mathrm{ pl}}^{2}v_{\mathrm{ hw}}\rho _{P} = \frac{2\pi R_{\mathrm{pl}}GM_{\mathrm{pl}}} {v_{\mathrm{hw}}} \rho _{P}, }$$

(7.14)

assuming that the surface escape velocity v _esc > v _hw and the 3D limit; and with the gas-free, planar, zero eccentricity limit:

$$\displaystyle{ \dot{M}_{\mathrm{gas-free}} \approx 11\sqrt{R_{\mathrm{pl } } R_{\mathrm{Hill } }^{3}}\varOmega _{K}\varSigma _{P} }$$

(7.15)

(Nishida 1983; Ida and Nakazawa 1989).

Although pebble accretion is fast and the rates increases with M _pl, the rates are not superlinear. If $\dot{M} \propto M^{\kappa }$ then κ = 1, 1∕2 and 2∕3 in Eq. (7.12) and Eq. (7.13), respectively. Only Safronov focusing is a runaway growth phenomenon (κ = 4∕3 for constant internal density); pebble accretion is not. However, the transition between Safronov-focusing and pebble accretion proceeds at a super-linear pace, since $\dot{M}_{\mathrm{3D}}$ is usually much larger than $\dot{M}_{\mathrm{Saf}}$ [see also Eq. (7.19)].

7.2.4 The Pebble Flux

The pebble accretion rates given above scale with the amount of pebbles that are locally available (Σ _P or ρ _P ). Because of their drift this quantity is expected to vary with time. It is useful to express the surface density in terms of the pebble mass flux through the disk $\dot{M}_{\mathrm{P,disk}}$:

$$\displaystyle{ \varSigma _{P} = \frac{\dot{M}_{\mathrm{P,disk}}} {2\pi rv_{\mathrm{drift}}(\tau _{s})}, }$$

(7.16)

where I have ignored diffusive transport .

A simple model for the mass flux $\dot{M}_{\mathrm{P,disk}}$ can be obtained from a timescale analysis (Birnstiel et al. 2012; Lambrechts and Johansen 2014). This entails that at any radius r dust grains coagulate into pebbles that start drifting at a size where the growth timescale t _growth exceeds the pebble drift timescale t _drift = r∕v _drift. This results in a mass flux $\dot{M}_{\mathrm{P,disk}} = 2\pi r_{0}\varSigma _{0}v_{\mathrm{dr,0}}$, where the subscript “0” refers to the radius where the pebbles enter the drift-dominated regime —the pebble front (Lambrechts and Johansen 2014)—and Σ ₀ is the initial density in solids. Clearly, r ₀ > r with r ₀(t) increasing with time, since coagulation proceeds slower in the outer disk.

The drift-limited solution (t _grow = t _drift; Birnstiel et al. 2012) also gives the (aerodynamic) size of the pebbles for r < r ₀ (the region where pebbles drift). Typically, pebble sizes are then τ _s ∼ 10⁻² (Lambrechts and Johansen 2014). However, it must be emphasized that all of this depends, to considerable extent, on dust coagulation physics—sticking properties, relative velocities , fragmentation threshold, internal structure, etc.; see Johansen et al. (2014) for a review—and also on the structure of the evolving outer disk. In this review I will not adopt a global pebble model, but formulate conclusions based on the local conditions of a growing planetary embryo.

7.2.5 The Pebble Isolation Mass

When the planet mass becomes large it will start to perturb the disk, changing the radial pressure gradient (∇_log P) in its vicinity. Clearly, when the perturbation becomes non-linear—planets massive enough such that their Hill radius exceeds the scale height of the disk, R _Hill > h _gas—a gap will open and a pressure maximum emerges upstream (Lin and Papaloizou 1986). Pebbles then stop their drift at the pressure maximum. The gap opening condition can be rewritten M _pl∕M _⋆ > (h _gas∕r)³, which translates into a pebble isolation mass of

$$\displaystyle{ M_{\mathrm{P,iso}} \sim 40\,M_{\oplus }\left (\frac{h_{\mathrm{gas}}/r} {0.05} \right )^{3}. }$$

(7.17)

for a solar-mass star. In a more detailed analysis, based on radiation hydrodynamical simulations, Lambrechts et al. (2014) and Bitsch et al. (2015a) argue for a numerical pre-factor of 20 M _⊕. For comparison, the classical isolation mass (valid for bodies that do not drift) is (Kokubo and Ida 2000):

$$\displaystyle{ M_{\mathrm{iso,clas}} \sim 0.16\,M_{\oplus }\:\left ( \frac{\tilde{b}} {10}\right )^{3/2}\left ( \frac{\varSigma _{\mathrm{solid}}} {10\,\text{g cm}^{-2}}\right )^{3/2}\left ( \frac{r} {\mathrm{AU}}\right )^{3}\left ( \frac{M_{\star }} {M_{\odot }}\right )^{-1/2}, }$$

(7.18)

where $\tilde{b}$ is distance between protoplanets in mutual Hill radii.

The pebble isolation mass is of great importance for the formation of giant planets. Since pebble accretion halts for M _pl > M _P,iso, it sets an upper limit to the heavy elements mass of giant planets. Reaching the pebble isolation mass, however, does not spell an end to giant planet formation . In contrast, it may even accelerate it, because the pre-planetary envelope has lost an important source of accretional heating and opacity. Gas runaway accretion sets in once envelope and core mass are similar (Rafikov 2006) and this may well be triggered soon after the pebble isolation mass is reached.

7.2.6 Summary: Accretion Regimes

Fig. 7.3

Sketch of the accretion regimes as function of the pebble aerodynamical properties (x-axis) and that of the planet(esimal) (y-axis). The dimensionless planet mass $\mathcal{M}_{\mathrm{pl}}$ (left y-axis) is defined as $\mathcal{M}_{\mathrm{pl}} = M_{\mathrm{pl}}/M_{t}$, where M _t is given by Eq. (7.10). The conversion to physical masses (right y-axis) holds for a radius of 1 AU and an internal density of ρ _• = 3 g cm⁻³. The primary dividing line is M _p = M _∗, distinguishing ballistic encounters, where gas-drag effects are unimportant, from settling encounters, where particles accrete by sedimentation. The line M _pl = M _hw∕sh indicates where Keplerian shear becomes important and the line Stk = 1 where aerodynamical deflection matters

Figure 7.3 summarizes the accretion regimes as function of the pebble dimensionless stopping time τ _s (x-axis) and the planet mass (y-axis). For the planet Eq. (7.10) has been used to convert to a dimensionless mass $\mathcal{M}_{\mathrm{pl}}$. Lines of M _pl = M _∗ and M _pl = M _hw∕sh are invariant in terms of the dimensionless $(\tau _{s},\mathcal{M}_{\mathrm{pl}})$, but not in terms of the physical mass. Now consider a small planetesimal (e.g. 1 km) that accretes pebbles of a certain stopping time (e.g. τ _s = 0. 1). Initially, it accretes those pebbles with the geometric cross section (σ _col ∼ πR _pl ²), but at:

• M _pl = R _pl v _hw ²∕2G (v _esc = v _hw) accretion switches to the so-called Safronov regime , where gravitational focusing enhances the collisional cross section by a factor of (v _esc∕v _hw)². Pebble accretion commences at

• M _pl = M _∗ [Eq. (7.11)], where ballistic accretion gives way to accretion by settling. This transition is abrupt.⁴ Specifically, the boost obtained from crossing the M _pl = M _∗ line is:

  $$\displaystyle{ \left ( \frac{\dot{M}_{\mathrm{3D}}} {\dot{M}_{\mathrm{Saf}}}\right )_{M_{\mathrm{pl}}=M_{{\ast}}} \sim \frac{\tau _{s}^{2/3}} {R_{\mathrm{pl}}/R_{\mathrm{Hill}}} \sim 100, }$$

  (7.19)

  at 1 AU. Accretion proceeds in the headwind regime at a rate given by Eqs. (7.12) or (7.13), dependent on the thickness of the pebble disk. At

• M _pl = M _hw∕sh [Eq. (7.9)], pebble accretion switches to the shear limit. Pebble accretion continues until

• M _pl = M _P,iso [Eq. (7.17)], where the pebble isolation mass is reached.

The ballistic:settling transition heralds the onset of pebble accretion. From Eq. (7.10) it follows that the transition occurs at a larger mass for increasing orbital radius. Visser and Ormel (2016) have calculated a more precise expression for the radius R _PA where pebble accretion commences:

$$\displaystyle{ R_{\mathrm{PA}} \approx \: 520\,\mathrm{km}\:\left ( \frac{v_{\mathrm{hw}}} {50\,\mathrm{m\,s}^{-1}}\right )\left ( \frac{\rho _{\bullet }} {\text{g cm}^{-3}}\right )^{-0.36}\left ( \frac{r} {\mathrm{AU}}\right )^{0.42}\tau _{ s}^{0.28}. }$$

(7.20)

Once pebble accretion commences, the jump in $\dot{M}$ is also more dramatic in the outer disk (Eq. (7.19), since R _pl∕R _Hill is lower). In addition, for the outer disk, aerodynamic deflection is less of an issue since pebbles will have a larger stopping time, because of the lower gas density.

7.3 Results

I illustrate the outcome of pebble accretion with a series of contour plots, where contours of a quantity Q are plotted as function of planet mass and particle size . Instead of the order-of-magnitude expressions derived above, I employ more precise expressions that have been calibrated to numerical integrations (Ormel and Klahr 2010; Ormel and Kobayashi 2012; Visser and Ormel 2016). But many of the key features highlighted in Fig. 7.3 will resurface.

I adopt the following disk profiles for the gas surface density and midplane temperature:

$$\displaystyle{ \varSigma _{\mathrm{gas}} = 10^{3}\,\text{g cm}^{-2}\left ( \frac{r} {\mathrm{AU}}\right )^{-1};\qquad T = 300\,\mathrm{K}\:\left ( \frac{r} {\mathrm{AU}}\right )^{-1/2} }$$

(7.21)

and take the disk headwind to be v _hw = 50 m s⁻¹. I further assume that planetesimals’ internal density increases according to:

$$\displaystyle{ \rho _{\bullet }(R_{\mathrm{pl}}) = 0.08\,\text{g cm}^{-3}\left (\frac{R_{\mathrm{pl}}} {\mathrm{km}} \right )^{0.5}, }$$

(7.22)

which crudely interpolates between “porous planetesimals” and rocky planets. The internal density of pebbles is taken to be ρ _• = 1 g cm⁻³. The standard value of the turbulent strength is α _T = 10⁻⁴.

7.3.1 The Collision Cross Section

Fig. 7.4

Collision factor f _coll: the collision cross section with respect to the geometrical cross section at 1 AU. The thick dashed line delineates the ballistic regime from the settling regime. Note the sharp increase in f _coll across this line at higher t _stop

First, in Fig. 7.4, the collision cross section, normalized to the geometrical cross section, is plotted, f _coll = (b∕R)², for r = 1 AU. The lower x-axis now gives the pebble radius (in cm) and the upper x-axis translates this to dimensionless stopping time . Remark that the tick marks for τ _s are much denser spaced beyond τ _s = 10⁻², because of the transition to Stokes drag. The y-axis again gives the planet mass or radius. The thick, dashed, black line denotes the transition between the ballistic and the settling regimes .

Many of the features of Fig. 7.3 can also be identified in Fig. 7.4. Below R _pl ∼ 100 km the cross section is that of the geometrical cross section (white area). Also, a steepening of the ballistic:settling transition (the dashed line) occurs below 1 mm, where aerodynamic deflection becomes important. Indeed, the collisional cross section can become very low. While micron-size dust grains may be produced by (colliding) planetesimals, they are not accreted by them! However, in a turbulent medium particles will collide more easily to the planetesimal (Homann et al. 2016). This effect is not included here.

In any case, it is clear that aerodynamically very small particles (τ _s ∼ 10⁻⁵–10⁻⁶) are hard to accrete and that settling (pebble accretion) of small particles gives low f _coll (upper left corner). This simply reflects the strong coupling to the gas, which is not accreted. Rates are much larger for bodies that accrete larger pebbles (τ _s ∼ 10⁻³–1) in the settling regime, which happens when the planetesimal crosses ∼ 100 km. In particular, at this ballistic:settling transition accretion rates jump dramatically. For example, from R _pl = 200 to 400 km and τ _s = 0. 1 f _coll increases a 100-fold [see also Eq. (7.19)]. Once f _coll ∼ 10⁴ (top right corner) pebbles are accreted at the (maximum) Hill cross section, σ _col ∼ R _Hill ².

7.3.2 Accretion Efficiencies: 2D and 3D

Does a large accretion cross section also imply a high accretion rate? For pebble accretion this is a difficult question to answer since pebbles drift. The accretion rate [Eq. (7.12)] depends on the surface density of pebbles Σ _P that are locally available. Due to their drift, pebbles are constantly rejuvenated: old pebbles leave the accretion region while new pebbles from the outer disk drift in. The question how large accretion rates are at a certain time therefore depends on the evolution of all solids. Analytical approaches (which work for smooth disk; see Sect. 7.2.4) or numerical ones (Birnstiel et al. 2012; Dra̧żkowska et al. 2016; Sato et al. 2016; Krijt et al. 2016) have also been developed.

However, even though the accretion rate requires a global model, a useful local quantity can still be defined: the pebble accretion efficiency or accretion probability P _eff. This is simply the pebble accretion rate on the planet [Eq. (7.12)] divided by the pebble accretion rate through the disk:

$$\displaystyle{ P_{\mathrm{eff}} = \frac{\dot{M}} {\dot{M}_{\mathrm{P,disk}}} = \frac{\dot{M}} {2\pi rv_{\mathrm{drift}}\varSigma _{P}}, }$$

(7.23)

where $\dot{M}$ is given by either Eq. (7.12) or Eq. (7.13). Note that Eq. (7.23) is independent of Σ _P . An efficiency of P _eff ≥ 1 guarantees accretion of the pebble. On the other hand, when P _eff ≪ 1 most pebbles avoid capture to continue their radial drift to the star.

Fig. 7.5

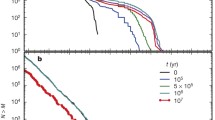
The efficiency of pebble accretion or accretion probability P _eff for (a) the 2D limit (pebbles reside in the midplane) and (b) for the general 3D case with our standard α _T = 10⁻⁴ for 10 AU. Values around 1 indicate very efficient accretion, while P _eff ≪ 1 indicates most pebbles drift to the interior disk, instead of being accreted. The thin-dashed line in (b) indicates the transition between 2D and 3D accretion (h _p = b _col)

In Fig. 7.5a contours of P _eff are plotted in the 2D-limit ($\dot{M} =\dot{ M}_{\mathrm{2d}}$). In the 2D limit it is assumed that the pebbles have settled to the disk midplane, which would be the case for a laminar disk. As is clear from Fig. 7.5a a pebble is more likely to be accreted by a larger planet(esimal), which is obvious. Much less obvious is the trend in the horizontal direction. On the one hand, large pebbles result in larger cross sections, increasing $\dot{M}_{\mathrm{2d}}$, but in the 2D limit $\dot{M}_{\mathrm{2D}}$ is sublinear in τ _s , $\dot{M}_{\mathrm{2D}} \propto \tau _{s}^{1/2}$ or ∝ τ _s ^2∕3 [Eq. (7.13)]. On the other hand, the drift velocity is linear in τ _s [Eq. (7.2)]. Hence, the drift dependence wins out: smaller pebbles are more likely to be accreted.

However, even for moderate turbulence accretion may well proceed in the 3D limit: the pebbles are distributed in a vertical layer of thickness larger than the impact radius b _col. Correspondingly, a scale height correction is applied to get a net accretion rate of:

$$\displaystyle{ \dot{M} =\dot{ M}_{\mathrm{2D}} \frac{b_{\mathrm{col}}} {b_{\mathrm{col}} + h_{\mathrm{peb}}\sqrt{8/\pi }}, }$$

(7.24)

where h _peb is the scale height of the pebble layer (Dubrulle et al. 1995; Cuzzi et al. 1993; Youdin and Lithwick 2007):

$$\displaystyle{ h_{\mathrm{peb}} = \sqrt{ \frac{\alpha _{T } } {\alpha _{T} +\tau _{s}}}h_{\mathrm{gas}}. }$$

(7.25)

The form of $\dot{M}$ adopted in Eq. (7.24) ensures the 2D and 3D expressions in the limits of b _col ≫ h _peb (2D) and b _col ≪ h _peb (3D), respectively.

The scale height-corrected accretion probability is presented in Fig. 7.5b. The 3D probability is always lower than the 2D limit and the lines are more horizontal. Even Earth-mass planets accrete pebbles rather inefficiently, meaning that a large pebble flux is needed for these planets to grow. For fixed planet mass the pebble size where b _col = h _peb, i.e., the transition from 2D to 3D (thin dashed line), has the highest accretion probability.

7.3.3 The Pebble Accretion Growth Mass, M _P,grw

From the pebble accretion probability P _eff, I define

$$\displaystyle{ M_{\mathrm{P,grw}} = \frac{M_{\mathrm{pl}}} {P_{\mathrm{eff}}}, }$$

(7.26)

as the amount of pebbles needed to grow the planet. This is a very useful quantity since it immediately highlights where growth is slow or fast. For example, a very large M _P,grw—e.g., thousands of Earth masses—indicates a bottleneck for the growth of the planet, because it is unlikely that so many pebbles are available. On the other hand, low M _P,grw likely indicate that growth is rapid. To obtain the actual growth timescale, M _P,grw should be divided by the pebble flux $\dot{M}_{\mathrm{P,disk}}$. Guillot et al. (2014) already introduced Eq. (7.26) as the filtering mass: M _P,grw is also the mass in planetesimals needed to ensure accretion of a single pebble.

Fig. 7.6

Required mass in pebbles to grow a planet by pebble accretion as function of pebble size (x-axis) and planet mass (y-axis) at 10 AU for the standard disk model [Eq. (7.21)] and α _T = 10⁻⁴. Contours denote the total amount of pebbles in Earth masses needed to e-fold the planet’s mass and include the pebbles that are drifting past without accretion. In red regions, growth is likely to stall. Above the ballistic:settling dividing line (thick dashed) growth is significantly boosted but nevertheless requires tens-to-hundreds of Earth masses in pebbles. Above the thin dashed line pebble accretion reaches its 2D limit

In Fig. 7.6 M _P,grw is plotted for r = 10 AU. What is immediately obvious is that M _P,grw is very large just below the pebble accretion initiation threshold (the black dashed line). Clearly, geometric and Safronov accretion are not effective in growing planetesimals large; and the initiation of pebble accretion relies on the presence of a massive-enough seed that is produced by a process other than sweep up of small particles. Such a seed may result from classical self-coagulation mechanisms (i.e., runaway growth of planetesimals) or, more directly, from the high-mass tail of the planetesimal formation mechanism , e.g., by streaming or gravitational instabilities (Cuzzi et al. 2010; Johansen et al. 2015; Simon et al. 2016; Schäfer et al. 2017).

Even in the settling regime, the required pebble masses are substantial. Also note that M _P,grw refers only to one e-folding growth in mass. In general, growth from an initial mass M _ini to a final mass M _fin takes a total mass of

$$\displaystyle{ M_{\mathrm{P,tot}} =\int _{ M_{\mathrm{ini}}}^{M_{\mathrm{fin}} }M_{\mathrm{P,grw}}(\tau _{s},M)\mathrm{d}\log M }$$

(7.27)

in pebbles. For example, growth from 10⁻³ to 10 Earth masses involves almost 10 e-foldings. Clearly, giant planet formation by pebble accretion requires massive disks ; at least several hundreds of Earth masses are needed to form a 10 M_⊕ core. Also, the pebbles need to be of the right (aerodynamic) size. Pebbles of τ _s ≈ 1 are not very suitable, as they drift too fast. Smaller pebbles are preferred.

Fig. 7.7

Required pebble masses at 1 AU at standard (a) and high (b) turbulence levels. The α _T = 10⁻⁴ case is shown in Fig. 7.6

Figure 7.7a shows contours of M _P,grw at 1 AU. At 1 AU M _P,grw is significantly lower than at 10 AU, because the pebbles are more efficiently accreted. The larger P _eff is caused by (1) a higher probability of encountering the planet because of the smaller circumference (2πr); and (2) a reduced scale height of the pebble layer . However, it is especially below the ballistic:settling line where the change is the largest. Windmark et al. (2012) and Garaud et al. (2013) have hypothesized that some particles could cross the fragmentation/bouncing barriers that operate around τ _s = 1, because of fortuitously colliding with particles at low collision energies. To grow into planetesimals, these “lucky” particles, however, still need to grow fast. Ignoring the radial drift problem, and with some tuning of the parameters this could work at 1 AU, but for r ≫ 1 AU sweep up growth in the geometric and settling regimes becomes simply too slow, as is seen in Fig. 7.6.

Fig. 7.8

Required pebble masses at 10 AU for (a) strong turbulence and weak turbulence (b)

A major determinant for the efficacy of pebble accretion, and a key unknown, is the turbulence strength parameter, α _T . Since disks are observed to accrete onto their host stars , it has been hypothesized that disks are turbulent, with the turbulent viscosity providing the angular momentum transport . For example, the magneto-rotational instability (Balbus and Hawley 1991), which operates in sufficiently ionized disks, provides α _T ∼ 10⁻². However, the turbulence could also be hydrodynamically driven, such as the recently postulated vertical shear instability (Nelson et al. 2013; Stoll and Kley 2014), the spiral wave instability (Bae et al. 2016), or the baroclinic instability (Klahr and Bodenheimer 2006), which provide perhaps α _T ∼ 10⁻⁴. Or one could imagine layered accretion (Gammie 1996), of which the disk wind model has recently become popular (Bai 2014, 2016). In that case the midplane—relevant here—stays laminar. Given these uncertainties—indeed α _T is very hard to constrain observationally (Teague et al. 2016)—it is best to consider α _T as a free parameter and test how it affects the pebble accretion rates.

In Fig. 7.7b M _P,grw is plotted for α _T = 10⁻², which significantly reduces the spatial density in pebbles in the midplane and increases M _P,grw compared to the nominal α = 10⁻⁴ value. For $\tau _{s}\lesssim \alpha _{T} = 10^{-2}$ M _P,grw is very flat. The reason is that accretion is now in the 3D limit, where $\dot{M}$ is linear in both τ _s and M _pl—dependencies that cancel upon conversion to M _P,grw. Still, at 1 AU pebble accretion is relatively efficient. However, at 10 AU the dependence on α _T becomes more extreme. In Fig. 7.8 contours of M _P,grw are plotted for α _T = 10⁻² and α _T = 10⁻⁶, (the nominal α _T = 10⁻⁴ case is plotted in Fig. 7.6). From Fig. 7.8 it follows that the mass requirements are very high for turbulent disks (α _T = 10⁻²), but more comfortable for laminar disks (α _T = 10⁻⁶). For the outer disk in particular, the ability of pebble accretion to spawn planets strongly depends on the level of turbulence.

Fig. 7.9

This figure illustrates the dependence of the required pebble mass on the headwind parameter, v _hw—compare with Fig. 7.6, above

In addition to α _T , the pebble accretion efficiency is sensitive to the radial pressure gradient in the gas [∇_log P; see Eq. (7.4)]. In the case where the pressure gradient reverses—i.e., at a pressure maximum—pebbles will no longer drift inwards. It is clear that at these locations pebble accretion becomes very fast and the planet’ growth is given by the rate at which the pebbles flow in, $\dot{M}_{\mathrm{P,disk}}$. More generally, pebble accretion is quite sensitive to v _hw as Fig. 7.9 demonstrates. In Fig. 7.9 the disk headwind has been increased (a) or decreased (b) by a factor 2 with respect to the default v _hw = 50 m s⁻¹ (see Fig. 7.6). An increase by a factor 2 may arise, for example, from a corresponding increase in the temperature of the disk (hotter disks rotate slower). From Fig. 7.9 it is clear that v _hw affects (1) the pebble accretion rates in the settling regime and (2) the dividing line between ballistic and settling regimes. Pebble accretion can be triggered more easily and proceeds faster when v _hw is lower.

7.3.4 Summary

From these numerical experiments the following conclusions emerge:

• 1. Pebble accretion is generally an inefficient process. Not all pebbles are accreted .

• 2. The efficiency of pebble accretion and its capability to produce large planets strongly depends on the vertical thickness of the pebble layer , which is determined by the disk turbulence. In particular in the outer disk, pebbles simply drift past the planet without experiencing an interaction. Efficiencies are also boosted in regions where the radial gas pressure gradient is small.

• 3. Pebble accretion is more efficient for particles of $\tau _{s}\lesssim 0.1$. Specifically, for a given mass, pebble accretion is most efficient for particle sizes where the growth modes switches from 2D to 3D, i.e., where h _peb ≈ b _col.

• 4. Pebble accretion requires an initial seed that must lie above the M _pl = M _∗ line [Eq. (7.20)] distinguishing ballistic from settling encounters. Such a seed must be produced from the planetesimal formation process or (failing that) by classical coagulation among planetesimals. The pebble accretion initiation mass is much larger in the outer disk.

7.4 Applications

I close this chapter with a brief recent overview of applications of pebble accretion.

7.4.1 Solar System

Lambrechts et al. (2014) argue that that the pebble isolation mass [Eq. (7.17)]—the upper limit at which planetary cores can accrete pebbles—naturally explains the heavy element contents in the solar system’s outer planets. After this mass is reached, pebble accretion shuts off; and the lack of accretional heating (and arguably opacity) will trigger runaway accretion of H/He gas. In their model, Uranus and Neptune never reached M _P,iso and accreted pebbles during the lifetime of the disk. Their arguments rely on an efficient accretion of pebbles (indeed they do consider the 2D limit), which means that turbulence levels had to be low or that the solar nebula contained massive amounts of pebbles.

A key parameter in the pebble accretion scenario is the size and number of the initial seeds. Here, the classic planetesimal-formation model has the advantage that growth proceeds through a runaway growth phase, where the biggest bodies outcompete their smaller siblings, since $\dot{M}_{\mathrm{Saf}}$ is superlinear [Eq. (7.14)]. However, pebble accretion is a more “democratic” process; embryos will tend to stay similar in terms of mass (Sect. 7.2.3). This was demonstrated by the N-body simulations of Kretke and Levison (2014), in which the pebbles were shared more-or-less evenly among the growing embryos, resulting in a bunch of Mars-to-Earth size planets, but not the ∼ 10 M _⊕ needed to form gas giants.

A way to remedy this problem is to invoke classical planet formation concepts. In Levison et al. (2015a) pebbles were fed into the simulation on much longer timescales ( ∼ Myr), resulting in the dynamical excitation of especially the smallest embryos. Pebbles then were preferentially accreted by the largest embryos, recovering the “winner-takes-it-all” feature that giant planet formation requires. This, so-called “viscously-stirred pebble accretion” (essentially a blend between classical planetesimal accretion and pebble accretion) was also applied to the inner solar system (Levison et al. 2015b). Here, the authors claim to have found a possible solution to the persistent “small Mars” problem (e.g. Raymond et al. 2009) by reversing the mass-order of planetary embryos: more massive embryos can form further in because accretion is more efficient. Although encouraging, it must be emphasized that these N-body models contain a great number of free parameters—ranging from the initial size-distribution of planetesimals, their location in the disk, to the properties of the pebbles and the gas—which means a proper investigation would imply a (prohibitively?) large scan of the parameter space.

Adopting a more basic approach, Morbidelli et al. (2015) claimed that solar system’s “great dichotomy”—small Mars next to big Jupiter—naturally follows from pebble accretion. The key feature is the iceline. Pebbles (τ _s ) as well as the pebble flux ($\dot{M}_{\mathrm{P,disk}}$) are large exterior to it; the first because of the fragmentation velocity threshold of silicate vs icy grains and the second because the pebbles lose their ice after crossing the iceline. Morbidelli et al. (2015) find that the τ _s = 10^−1. 5 pebbles beyond the iceline accrete more efficiently than the smaller pebbles (τ _s ≈ 10^−2. 5) interior to it (Fig. 7.6, albeit for different disk parameters, gives the gist of their result). Hence, Jupiter’s core grows faster than Mars’ and eventually, when it opens a gap, will starve the inner disk of pebbles. A similar result, using a more elaborate model, was found by Chambers (2016).

7.4.2 Exoplanetary Systems

7.4.2.1 Super Earths

One of the key surprises of the last decade has been the discovery of the super-Earth planet population (Fressin et al. 2013; Petigura et al. 2013): close-in planets (r ∼ 0. 1 AU) of mass between Earth and Neptune, which are rock-dominated but often have a gaseous envelope (Lopez et al. 2012). Because super-Earths orbit their host stars at close distance, there is no longer a timescale problem for their assembly—even without gravitational focusing coagulation proceeds fast. In the classical in situ model there is however a mass budget problem and to form super-Earths in situ the canonical Minimum-Mass Solar Nebula surface density profile (Weidenschilling 1977b; Hayashi 1981) has to be cranked up (Chiang and Laughlin 2013). Another challenge is that the isolation masses at ∼ 0. 1 AU are very small and that embryos need to merge at a later stage through giant impacts, while preserving their hydrogen/helium atmospheres (Inamdar and Schlichting 2015; Lee and Chiang 2016).

In the context of the pebble accretion model super-Earths formation at/near the inner disk edge seems very natural. The idea is that pebbles drift inwards until they meet a pressure maximum. This could simply be the disk edge (provided pebbles do not evaporate!) or an MRI active/dead transition region (Kretke and Lin 2007; Chatterjee and Tan 2014; Hu et al. 2016). At the pressure maximum, mass piles up until gravitational instability is triggered. Pebble accretion then proceeds until the pebble isolation mass [Eq. (7.17)], which indeed evaluates to super-Earth masses. An advantage of pebble migration over planet migration is that pebbles, due to their coupling to the gas, avoid trapping in mean motion resonance, which is needed to explain those very compact systems. However, to reproduce the exoplanet architecture in a framework that includes Type I migration remains challenging (Ogihara et al. 2015; Liu et al. 2017).

Fig. 7.10

Pebble mass reservoir to grow planets in the outer disk

7.4.2.2 Distant Planets

Another hallmark of the exoplanet field has been the discovery of distant planets, of which the HR-8799 system is the poster boy (Marois et al. 2008, 2010). HR-8799 harbors four super-Jupiter planets at, respectively, 15, 24, 38, and 68 AU—too far to form with the classical core-accretion model. It has therefore been proposed that these planets formed from a gravitational unstable disk (Dodson-Robinson et al. 2009; Boss 2011). Pebble accretion of the resulting clumps can accelerate their collapse, because the accretion effectively cools the clump (Nayakshin 2016). Pebble accretion may also re-invigorate the core-accretion model, provided the disk is laminar. In Fig. 7.10 the required pebble masses for moderate (α _T = 10⁻⁴) and very low turbulence levels (α _T = 10⁻⁶) are given. For moderate turbulence, pebble accretion requires a pebble reservoir of hundreds of Earth masses, while in the laminar case accretion becomes quite efficient when the particles are of sub-mm size. Although challenging, forming these distant planets by pebble accretion cannot be dismissed at first hand.

7.4.2.3 Population Synthesis Models

The assembly of a solid core is a critical (albeit not the only!) part of planet population synthesis models (see, e.g., Ida and Lin 2004; Mordasini et al. 2009 and their sequels). Because they rely on the classical (planetesimal-driven) scenario, sufficiently large planetary embryos can only form around ∼ 5 AU (because of the isolation mass constraint [Eq. (7.18)]. On the other hand, as also discussed in Sect. 7.1.3, accretion is getting progressively slower in the outer disk.⁵ Consequently, there is a limited range in the disk where giant planets can form; and success relies on fortuitous placement of initial seeds in massive disks (Bitsch et al. 2015b).

Because of pebble drift, growing cores have in principle access to the entire solid mass of the disk. This, according to Bitsch et al. (2015b), makes pebble accretion attractive. From the results described in this review, it is clear that success also depends on the turbulent state of the (outer) disk and on the existence of a massive pebble reservoir ; but it is true that once conducive conditions materialize there is no longer a timescale problem. In addition Bitsch et al. (2015b) find a prolific formation of super-Earths and ice giants . Recently, pebble accretion-driven models have also been adopted to understand the composition and chemistry of Jupiter-size planets (Madhusudhan et al. 2016; Ali-Dib 2017)—a potentially observable characteristic. However, any population synthesis model is as strong as its weakest link. In this regard, key concerns are the lack of a physical model for the formation of the seeds and the hyper-sensitivity of the synthesized planet population to the prescription for planet migration (Coleman and Nelson 2014). Nevertheless, accounting for pebble accretion opens up new avenues to understand the exoplanet population as a whole.