5.1 Introduction

Dust coagulation is the first step in planet formation . Dust grains are solid materials in molecular cloud cores composed of silicates, water ice , carbonaceous materials and others. These solid bodies measure ∼ 0.1–1 μm (e.g., Mathis et al. 1977). During the star formation process via gravitational collapse of a molecular cloud core, the tiny solid bodies are dragged by gas and accrete to the circumstellar disk around the young star . In the gas disk , dust grains stick to each other to form larger bodies , owing to their frequent collisions due to high solid density. This hit-and-stick process ultimately causes planets to form (e.g., Weidenschilling 1977; Hayashi 1981). We aim to reveal that this dust coagulation process forms planets using astronomical observations, theoretical studies, and laboratory experiments.

There are an enormous number of problems during dust coagulation depending on size. The size of the solid bodies ranges from 0. 1 μm to 1000 km, which is 13 orders of magnitude in size and thus 39 orders of magnitude in mass. The dynamics of the solid bodies is determined by the friction between gas and dust, which depends of course on the size of the solid bodies. Thus, there are different problems corresponding to each grain size range.

The first problem is the charge barrier, where negatively charged particles cannot collide with other particles because the electrostatic repulsive force is high enough to avoid the collisions (Okuzumi 2009; Okuzumi et al. 2011a,b). The radial drift problem appears when dust grains range from millimeters to meters in size. These dust grains are decoupled from the gas, which results in facing the gas drag in an azimuthal direction. This reduces the angular momentum of the grains and they migrate to the central star , prohibiting further growth because the time scale of radial migration is shorter than the growth time scale (Adachi et al. 1976; Weidenschilling 1977). There are also problems due to microphysics of dust collisions, which are fragmentation and bouncing. If the collisional energy of dust grains is high enough to disrupt the grains, dust grains cannot grow further. The threshold velocity of fragmentation is a few meters per second for silicate-like aggregates , much smaller than the typical highest collision velocity of ∼ 50 m s−1 in disks (Blum and Münch 1993; Blum and Wurm 2008; Wada et al. 2007, 2009, 2013). Dust grains of some size ranges do not stick, but rather bounce (Güttler et al. 2010; Zsom et al. 2010). Even if these problems are solved and kilometer-size planetesimals are successfully formed, there are problems with the migration of protoplanets and others, which are beyond the scope of this chapter.

There have been many attempts to solve these problems: streaming instability (e.g., Johansen et al. 2007), direct coagulation with high dust-to-gas ratio (e.g., Brauer et al. 2008), pressure trapping (e.g., Whipple 1972; Pinilla et al. 2012), vortex trapping (e.g., Lyra et al. 2009), dead zone edge (Dra̧żkowska et al. 2013), lucky particle approach (Windmark et al. 2012), growth by condensation close to snow-lines (Ros and Johansen 2013), direct formation of planets through gravitational instability (Boss 2000), etc. We do not exclude any of these possibilities, but we discuss another topic in this chapter: porosity evolution.

Dust grains have usually been assumed to have a constant internal density during dust coagulation for simplicity. Readers can picture this by thinking about the evolution of water droplets. Two spherical water droplets stick to each other to form larger spherical water droplets with the same density. However, dust grains are not liquid but solid. The dust grains are mainly composed of water ice , which has a sublimation temperature of ∼ 150 K at the pressure in the disk, which corresponds to a location at ∼ 1 AU from the central star . Even inside the snowline, the dust grains are composed of silicates, which have a sublimation temperature of ∼ 1700 K. Therefore, when dust grains stick to each other, they naturally form pores inside. The aggregates of dust grains have lower internal density, which equates to a lower volume filling factor. We note that the internal density ρ int is written as ρ int = ρ 0 f, where ρ 0 is the material density and f is the filling factor, and the porosity is given as p = 1 − f. This has a great effect on dust coagulation because the enhanced cross-section causes the frequent collisions to reduce the growth timescale and increase the friction against the disk gas to change the dynamics. Furthermore, it also changes the optical properties, which may change the interpretations of observations.

In this chapter, we discuss porosity evolution during dust coagulation in protoplanetary disks based on the recent progress in numerical studies. As a result, we argue that treating porosity evolution naturally solves many severe problems in planetesimal formation. In addition, we also discuss how it affects planetesimal formation and observations of protoplanetary disks . Finally, we also mention future directions of the study of porosity evolution.

5.2 Porosity Evolution

First, we describe our assumptions regarding dust grains. The first dust grains are assumed to be spherical dust grains with the same radius, called monomers. The monomers are assumed to be 0.1 μm in size and composed of water ice .

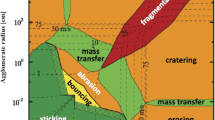
Porosity evolution is divided into four stages, as shown in Fig. 5.1. The first stage is the hit-and-stick. The relative velocity between two small dust grains is dominated by their thermal Brownian motion, which results in collisions with a velocity of ∼ mm/s. This collisional energy is not sufficient to restructure the aggregates because of the collisions. Therefore, one of the two colliding dust aggregates stays at the point where it first hits the colliding aggregate . Thus, at this stage, the porosity evolution is understood to be geometric growth. The filling factor evolution of sequential collisional growth can be understood as a function of the mass ratio of the two colliding aggregates. If the mass ratio of colliding aggregates is always unity, which corresponds to hitting the copy of the same aggregates from a random direction, this yields dust aggregates with the fractal dimension of ∼ 1.9 (e.g., Mukai et al. 1992). If the mass ratio approaches 0, at the other extreme, which corresponds to a monomer always hitting an aggregate, the fractal dimension yields ∼ 3. The former case is called ballistic cluster-cluster aggregation (BCCA) whereas the latter is called ballistic particle-cluster aggregation (BPCA). The nature of dust coagulation in planet formation is between these two types of aggregation and the question is which case describes the initial growth of dust grains well. Ormel et al. (2007) have performed a pioneering work on porosity evolution. In terms of porosity evolution, dust aggregates form porous dust aggregates , which have a filling factor of ∼ 1%, due to the simple interpolation for collisions in the intermediate aggregates between BCCA and BPCA. This was investigated later by numerical simulations of dust collisions (Okuzumi et al. 2009, 2012), which shows that similar-mass collisions lead to many more fluffy aggregates with fractal dimensions close to ∼ 2. As long as the dust coagulation occurs with similar-sized collisions, therefore, the dust aggregates become more and more porous because of hit-and-stick growth.

Fig. 5.1
figure 1

Schematic illustration of each stage of porosity evolution. (a) The dust aggregate hits another aggregate to coagulate. This reduces the dust density, and occurs in the early stage of dust growth. (b) When the collisional velocity is high enough to disrupt the dust aggregates, they are compressed. (c) The dust aggregate has a relative velocity with respect to the gas, and they feel the ram pressure of the gas. The ram pressure statically compresses the dust aggregates. (d) When the dust aggregates becomes so massive that they do not support their structures, they are compressed by their self-gravity. This figure is published as Fig. 2 in Kataoka et al. (2013a)

Full size image

The second stage is collisional compression. Once the collisional compression energy exceeds a critical energy to move one connection of monomers, the first restructuring occurs. The critical energy is that used to roll the monomers in contact, which is defined as rolling energy E roll (Dominik and Tielens 1997). This corresponds to the onset of collisional compressions. The mass and filling factor of the dust aggregates in typical protoplanetary disks are derived to be m ∼ 10−4 g and f ∼ 10−5. However, even when collisional compression occurs, dust aggregates are not compactified as much: the filling factor remains constant or continues to decrease (Suyama et al. 2008, 2012; Okuzumi et al. 2012). This can be understood as follows. When two dust aggregates collide, they create a new void region, which severely reduces the filling factor. Most of the collisional energy is consumed to compress this newly created void region. As a result, the pre-existing void regions are not very compactified. Even the collisional velocity increases with increasing Stokes number. This effect is not effective enough to compress the aggregates (Okuzumi et al. 2012); therefore, there must be other mechanisms to compress the porous dust aggregates .

The third and fourth stages are quasi-static compression processes. Dust aggregates always feel ram pressure from the disk gas. This ram pressure causes the aggregates to compress. For small filling factors, the compressive strength has been obtained by numerical simulations and is derived to be

$$\displaystyle{ \rho _{\mathrm{eq}} = \left ( \frac{r_{0}^{3}} {E_{\mathrm{roll}}}P\right )^{1/3}\rho _{ 0}, }$$
(5.1)

where ρ eq is the internal mass density of the aggregate, r 0 the monomer radius, E roll the rolling energy, P the compressive strength, and ρ 0 the material density of the dust grains (Kataoka et al. 2013b). The ram pressure can be written as

$$\displaystyle{ P_{\mathrm{gas}} = \frac{mv} {\uppi r^{2}} \frac{1} {t_{\mathrm{s}}}, }$$
(5.2)

where P gas is the ram pressure of the disk gas, m the mass of the aggregate, v the relative velocity between the gas and the aggregate, r the radius of the aggregate, and t s the stopping time . Equalizing these two equations, we can obtain the equilibrium filling factor (or internal density ), which represents the lower limit of the filling factor. In the same manner, the fourth stage of the self-gravitational compression can be understood. When dust aggregates become sufficiently massive, they are compressed by their own gravity. The pressure of the self-gravity of the

$$\displaystyle{ P_{\mathrm{grav}} = \frac{Gm^{2}} {\uppi r^{4}}, }$$
(5.3)

where P grav is the pressure due to self-gravity, G is the gravitational constant.

Combining these stages, we finally reveal the overall filling factor evolution in protoplanetary disks, as shown in Fig. 5.2 (Kataoka et al. 2013a). The 0.1-μm-sized dust grains become extremely fluffy dust aggregates with a filling factor of ∼ 10−5. The dust aggregates coagulate to form larger bodies maintaining the equilibrium filling factor at the ram pressure of the gas, which results in the filling factor of ∼ 10−4. Finally, when the dust aggregates become as massive as 1012 g, dust aggregates are compressed to form relatively compact bodies with f = 0. 1. Note that we stop the calculation at f = 0. 1 because the static compressive strength formula is applicable where \(f\lesssim 0.1\), whereas the pathway of the filling factor is expected to approach the filling factor of unity. Interestingly, the mass and filling factor of the resultant aggregates are in relatively good agreement with those of comets, which are believed to be the remnants of planetesimals (A’Hearn 2011). In this way, the overall filling factor evolution has been revealed, with the intermediate stage of extremely fluffy dust aggregates. We discuss how they avoid the radial drift barrier indicated in Fig. 5.2 in the next section.

Fig. 5.2
figure 2

The overall porosity evolution from 0.1 μm-sized dust grains to 10-km-sized planetesimals. The orbital radius is at 5 AU. The black, blue, and red solid lines correspond to hit-and-stick, gas compression, and self-gravitational compression of dust aggregates. The red shaded region represents where the growth time scale is shorter than the drift time scale. This figure is published as a part of Fig. 3 in Kataoka et al. (2013a)

Full size image

5.3 Growth Barriers in Dust Coagulation

We have revealed the overall filling factor evolution from dust grains to planetesimals . Here, we discuss how this fluffy growth is beneficial to avoiding growth barriers in planetesimal formation.

5.3.1 Radial Drift Barrier

The radial drift problem is that the dust growth time scale is larger than the migration time scale of dust grains, especially when the Stokes number becomes unity. The growth time scale is strongly affected by the gas drag law. The gas drag law is in the Epstein regime if the aggregate radius is less than the mean free path of the gas, whereas it is in the Stokes regime if the radius is larger than the mean free path of the gas. As long as the gas drag is in the Epstein regime, both growth and drift time scales depend on the mass-to-area ratio of dust aggregates. Therefore, even if the filling factor changes, the growth time scale is always larger than the drift time scale: the radial drift barrier is not avoidable. However, if the radius of dust aggregates exceeds the mean free path of the gas, then the gas drag law changes to the Stokes regime. In this regime, the growth time scale becomes shorter. On the pathway of the filling factor evolution, when the dust aggregates have a Stokes number of unity, the radius of the aggregates is ∼ 100 m, which is much larger than the mean free path of the gas, ∼ 1 m. More details can be found in Okuzumi et al. (2012). The region where the growth time scale is shorter than the drift time scale is shown in Fig. 5.2. The revealed pathway of filling factor evolution clearly avoids the radial drift barrier. Whether the radial drift problem is avoided depends on the location of the protoplanetary disks. Roughly speaking, rapid coagulation to avoid the radial drift barrier occurs within ∼ 10–20 AU but outside of the water snow line (see Okuzumi et al. 2012; Kataoka et al. 2013a).

5.3.2 Fragmentation Barrier

When two dust aggregates collide with a sufficiently high velocity, they are disrupted and lose their mass during the collision, which causes a problem with regard to grain growth . Theoretically, the minimum amount of energy required for catastrophic disruption of dust aggregates is calculated by assuming that the collision energy is equal to the energy needed to cut all the connections between the monomers in the aggregates, which is

$$\displaystyle{ E_{\mathrm{imp}} \sim 10n_{\mathrm{k}}E_{\mathrm{break}}, }$$
(5.4)

where E imp is the collision energy, n k is the number of all connections of the monomers, and E break is the energy required to cut one connection among monomers that are in contact (Chokshi et al. 1993; Dominik and Tielens 1997; Wada et al. 2007). As E imp is proportional to the mass, which is proportional to a number of monomers, and n k should be proportional to a number of monomers, the breaking-up velocity does not depend on mass. Therefore, for the catastrophic disruption, the threshold velocity has been intensively studied. Although the threshold velocity of fragmentation does not depend on the aggregate mass, it depends on materials and the size of the monomers.

Enormous efforts have been made with laboratory experiments that show that the threshold velocity of silicate grains is a few m s−1 (e.g., Blum and Münch 1993) and a few tens of m s−1 for ice (Gundlach and Blum 2015). In the series of numerical simulations (Wada et al. 2007, 2008, 2011), on the other hand, the final form of the threshold velocity for the net growth is revealed to be

$$\displaystyle{ v_{\text{col, crit}} = \left \{\begin{array}{@{}l@{\quad }l@{}} 80\left (r_{0}/0.1\,\upmu \mathrm{m}\right )^{-5/6}\quad &\ \mathrm{[m\,s}^{-1}]\ \mathrm{for\ ice}, \\ 8\left (r_{0}/0.1\,\upmu \mathrm{m}\right )^{-5/6} \quad &\ \mathrm{[m\,s}^{-1}]\ \mathrm{for\ silicate}, \end{array} \right. }$$
(5.5)

where r 0 is the monomer radius (Wada et al. 2013). This is in excellent agreement with the laboratory experiments.

We turn now from microphysics to astrophysical applications. The typical maximum collision velocity between dust aggregates depends on the disk models. The collisional velocity becomes maximal when the Stokes number of dust aggregates becomes unity. The maximum collisional velocity is mainly determined by the gas turbulent velocity at the midplane of the disk. The midplane temperature is significantly lower than the surface that is irradiated by stellar radiation (e.g., Chiang and Goldreich 1997). Considering this cold midplane, the typical maximum collisional velocity is around 30 m s−1. This indicates that the fragmentation problem is significant for silicate dust grains because the fragmentation threshold velocity is ∼ 1–8 m s−1 if we assume the monomer radius to be between 0.1 and 1 μm. However, the fragmentation problem can be avoided if we assume icy particles to have a small monomer size, because the fragmentation threshold velocity ranges from ∼ 10 to 80 m s−1 if we assume the monomer size to be between 0.1 and 1 μm. Therefore, as long as we assume 0.1-μm-sized icy particles, the fragmentation is not a problem for planetesimal formation.

Here, we should note how this could be consistent with the observations of protoplanetary disks , which suggest that they might be full of small grains (e.g, Dullemond and Dominik 2005). If we assume that the fragmentation is completely inefficient, this is not consistent with the observations. One way of solving this problem is to introduce partial fragmentations. The fragmentation threshold velocity in the series of numerical simulations (e.g., Wada et al. 2013) is defined by whether the target aggregates gain mass from the projectile, called net growth. Therefore, even if the collision velocity is lower than the fragmentation velocity, the dust aggregates still produce small fragments, and this may explain the observations. Another possibility is to introduce high mass ratio fragmentation, which could lead to many fragments being produced (Seizinger et al. 2013; Krijt et al. 2015). However, we should also mention that Wada et al. (2013) argue that the growth efficiency via fragmentation does not depend on the mass ratio of the colliding aggregates .

5.3.3 Bouncing Barrier

Bouncing behavior has been reported in laboratory experiments: when two dust aggregates collide, they do not stick, but rebound, which causes a problem with dust growth (Güttler et al. 2010; Zsom et al. 2010). On the other hand, bouncing behavior has not been observed in numerical simulations. However, Wada et al. (2011) found that extremely highly packed compact aggregates can bounce, even in numerical simulations. The transition between sticking and bouncing is determined by an average coordination number of dust aggregates; this is equivalent to how many monomers are connected to a single monomer. The critical coordination number for bouncing is 6 (Wada et al. 2011), which is realized only when dust aggregates are compact. The corresponding filling factor is uncertain, but is around f = 0. 3–0.6 (Wada et al. 2011; Seizinger and Kley 2013; Kothe et al. 2013). Therefore, as long as the filling factor is less than ∼ 0.3–0.6, bouncing does not occur. This is always valid if the filling factor evolution is as described in the previous section. Thus, bouncing is not a barrier to growth if we include porosity evolution in dust coagulation.

5.3.4 Short Summary and Discussion

We have discussed the notion that planetesimal formation via direct coagulation is possible if we include porosity evolution. The conditions are such that the monomer size is ∼ 0.1 μm, the monomers are composed of ice to avoid the fragmentation barrier, and the location of planetesimal formation should be within 10–20 AU in protoplanetary disks to avoid the radial drift barrier. Of course, this does not fully solve the planetesimal formation problems, but this certainly gives us a theory that planetesimals form under certain conditions. Furthermore, this asks us another question: what are we looking at through radio observations? If porosity evolution is correct, it is applicable even for the outer radius, which means that the emission may be coming not from compact spheres, which has usually been assumed, but from fluffy aggregates . This also gives us an opportunity to test the fluffy growth scenario. We discuss this point in the next section.

Also, we discuss the assumptions and limitations of the numerical and theoretical modeling that we used in this work. First of all, the monomers are always assumed to have a single size in the numerical simulations. In reality, however, the monomers also have a size distribution and whether the behavior is characterized by a representative size is uncertain. Furthermore, owing to the limitation of the number of monomers that we can treat in numerical simulations, the parameter space of mass and filling factor has not been completely studied. Moreover, the mass ratio of the projectile and the target and off-center collisions has been studied, but is still under discussion. Readers should also see the papers that we did not discuss in this chapter (Paszun and Dominik 2009; Seizinger et al. 2013; Ringl et al. 2012), and should be cautious about the assumptions that we and other authors have made.

5.4 Opacity Evolution

Observations of protoplanetary disks have revealed the dust and gas structure. To measure grain size in particular, the spectral index at millimeter wavelengths is key. The opacity of dust grains at millimeter wavelengths becomes flatter with increasing grain size (Miyake and Nakagawa 1993). The opacity index β has been shown to be ∼ 0–1 for protoplanetary disks (Beckwith and Sargent 1991) if the disk is optically thin . This indicates a significant dust growth to millimeters in size from the interstellar medium where the grain size is in microns (Pollack et al. 1994). These results are supported by later interferometric observations with high spatial resolution (e.g., Andrews and Williams 2007; Isella et al. 2009; Ricci et al. 2010a,b; Guilloteau et al. 2011). However, if the dust grains are not compact, are they really millimetric? To answer the question, in this section, we describe the dependence of the absorption opacity of dust aggregates on their filling factor.

To calculate the opacity of dust aggregates precisely, we need to use special calculations such as discrete dipole approximation (DDA; Draine 1988) and the T-matrix method (TMM; Mackowski and Mishchenko 1996). There are many applications of calculations of dust grains in the context of dust grains in disks (e.g., Mukai et al. 1992; Min et al. 2005, 2007). Here, we want to investigate at least the millimeter-sized grains, which are composed of 1012 of 0.1 μm-sized monomers. However, the calculations are limited by computer power and it is impossible to calculate the opacity of dust aggregates composed of such a large number of monomers. We therefore use a simpler method, which is the effective medium theory (EMT).

The EMT method is a mixing rule to compute the effective refractive index of the aggregates. The EMT approximation should be valid as long as the substructure (i.e., monomer scale) is much smaller than the wavelengths. In addition, especially for the absorption opacity, the EMT has good agreement with DDA and TMM (Kozasa et al. 1992). Here, we consider the absorption opacity of dust aggregates that are composed of micron-sized monomers at millimeter wavelengths . Therefore, the EMT approximation should be valid.

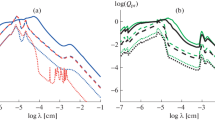
Figure 5.3 represents the absorption opacity of dust aggregates where the aggregate radius a and the filling factor f have values of (a, f) = (1 mm, 1. 0), (1 cm, 10−1), (10 cm, 10−2), (1 m, 10−3), (10 m, 10−4). The absorption opacities are a good match for the five lines except for the compact grains at ∼ 1 mm. This indicates that as long as the product of af is constant, the absorption opacity is degenerated even if the filling factor is changed. We have also derived a semi-analytical formula and confirm the fact that the absorption opacity is characterized by af except for the compact grains at the wavelengths of λ = 2πa (see Kataoka et al. 2014). We also note that Cuzzi et al. (2014) obtained similar conclusions on the opacity of porous dust aggregates.

Fig. 5.3
figure 3

The absorption opacity of dust aggregates is af = 1 mm, where the aggregate radius is a and the filling factor is f. There are five parameter sets, where (a, f) = (1 mm, 1. 0), (1 cm, 10−1), (10 cm, 10−2), (1 m, 10−3), (10 m, 10−4) presented in the same figure. This figure is published as a part of Fig. 3 in Kataoka et al. (2014)

Full size image

This tells us that we could possibly distinguish between compact spherical grains and porous dust aggregates with the filling factor of \(\lesssim\) 0.1. Figure 5.4 shows an opacity index profile as a function of a max f. The opacity index β is ∼ 1.7 for both compact grains and porous dust aggregates. In the case of compact grains, as dust size increases, the opacity index β is enhanced to be ∼ 2.7 at the size of a max f ∼ 0. 7 mm, and then decreases with increasing size. In the case of porous dust aggregates, however, the opacity index β monotonically decreases with increasing size. Therefore, if the opacity index of an intermediate size such as a max f ∼ 0. 7 mm is constrained, we can distinguish between spherical compact bodies and porous dust aggregates \(f\lesssim 0.1\). This could be possible by measuring the radial dependence of β in protoplanetary disks. The growth timescale is shorter at inner radii, and longer for outer radii. Therefore, the radial profile of β roughly corresponds to the β as a function of different grain sizes. There have been some observational constraints on the radial profile by using interferometric observations at radio wavelengths, which shows that β is small inside the disk and large outside the disk (e.g., Isella et al. 2010; Guilloteau et al. 2011; Pérez et al. 2012, 2015; Tazzari et al. 2016). The results are still consistent with both compact and porous dust models. Future observations with higher angular resolution and greater sensitivity would reveal whether grains are compact or not.

Fig. 5.4
figure 4

The dust opacity index β as a function of a max f, where a max is the maximum aggregate radius when af is constant. The aggregate size distribution is assumed to be n ∝ (af)−2. This figure is published as a part of Fig. 11 in Kataoka et al. (2014)

Full size image

5.5 Future Directions

Based on numerical and theoretical modeling, we argue that dust grains coagulate to form extremely fluffy aggregates in protoplanetary disks. These fluffy aggregates account for the observed radio emission, but the porosity and mass are highly degenerated in emission and it is hard to distinguish between compact grains and fluffy aggregates from continuum emission .

First, we must determine the size of the monomers. The fragmentation barrier is avoided if the monomer size is as small as 0.1 μm. However, the barrier is still severe if the monomer size is as large as 1 μm. Therefore, it is important to determine the monomer size in protoplanetary disks. There have been some studies aimed at constraining the micron-sized particles . For instance, infrared emission of dense molecular cores is well explained by intensity scattered by micron-sized dust grains (e.g., coreshine effect; Pagani et al. 2010). For another example, infrared-scattered emission of protoplanetary disks is significantly fainter than expected, which is explained well by the backward scattering of a few micron-sized particles (Mulders et al. 2013). However, this analysis is based on the assumption that dust grains are compact. If they are aggregates, the infrared scattering opacity could be enhanced by the aggregated structure (Köhler et al. 2012) and the scattering properties are determined by the monomer size (Min et al. 2016; Tazaki et al. 2016).

Second, the porosity of dust aggregates should be measured in observations of protoplanetary disks. The radial profile of the opacity index β could distinguish between spherical bodies and porous aggregates. However, once the filling factor becomes less than ∼ 0.1, it is impossible distinguish. To measure the porosity, we have to know information on both the absorption and the scattering opacity: the absorption opacity tells us the mass-to-area ratio (equivalent to af) of dust aggregates (Kataoka et al. 2014), whereas the scattering opacity tells us the size of the aggregates (Tazaki et al. 2016). Although there had been no way of constraining the scattering opacity of large grains or aggregates, we recently proposed that millimeter-wave polarization of protoplanetary disks could be due to dust scattering (Kataoka et al. 2015).

Finally, it is also important to compare the porous planetesimals as a result of porosity evolution with comets in the solar system. Comets are believed to be remnants of planetesimals. We have already compared the mass and filling factor relation, which shows a filling factor of 10–50% (see A’Hearn 2011, and references therein). Nowadays, thanks to the Rosetta mission, an enormous amount of information on the comet 67P/Churyumov-Gerasimenko has been successfully obtained, which could constrain the formation history of comets (e.g., Thomas et al. 2015).