Keywords

1 Introduction

The ABC analysis is a popular and widely used technique for the inventory classification problem and categorizes inventory items into three groups: A, B, or C based on some criteria in order to establish appropriate levels of control over each group.

For some time now, several metaheuristics have been deployed to tackle the MCIC problem. Tsai and Yeh [31] uses the particle swarm optimization technique and presents an inventory classification algorithm that simultaneously search the optimum number of inventory classes and perform classification, while Mohammaditabar et al. deploys the simulating annealing method [24] and proposes an integrated model to categorize the items and at the same time find the best policy. Saaty [30] has developed the Analytic Hierarchy Process (AHP) method, which has been widely deployed by some researchers to tackle the MCIC problem [4, 7, 8, 27, 28]. Other researchers [12, 14, 15] used a fuzzy version of the AHP method (FAHP). Lolli et al. [22] established a multi-criteria classification model called AHP-K-Veto, based on the AHP method and the K-means algorithm. Bhattacharya et al. [3] developed a model which combines Topsis (Technique for Order Preferences by Similarity to the Ideal Solution) with AHP method in order to generate a ranking items and then an ABC classification. Chen et al. [6] proposed an alternative approach to MCIC problem by using Topsis and two virtual items. Guvenir and Erel [9] developed a method that uses the generic algorithm for the sake of learning criteria weight, and established cut-off points between the classes A-B and B-C, in order to generate a classification of items. Then they showed in a second study [10] that their method based on genetic algorithm gives better performance than the AHP method. Al-Obeidat et al. [1] proposed an hybrid model which combine Differential Evolution method with the PROAFTN method, by using the evolutionary algorithm to inductively obtain PROAFTN’s parameters from data to achieve a high classification accuracy. Liu et al. [21] combined the methods of Electre III and the simulating annealing to deal with the compensatory effect of the items against criteria and opted for grouping criteria. A new MCDM method of Evaluation based on Distance from Average Solution (called EDAS) [19] is introduced by calculating the best alternative according to the distance from positive and negative solutions.

To the best of our knowledge, the Artificial Bee Colony algorithm [16–18] and the VIKOR method [23, 26, 32] were not used to solve the ABC MCIC problem. In this paper, we present a new hybrid approach based on these two methods, which attempt to combine the main advantages of each used method. In our approach, the multi-criterion decision problem is modeled by using Vikor model whose parameters are tuned by using a bee colony optimization algorithm. Each established classification is evaluated by using an estimation function based on the inventory cost and the fill rate service level [2], which also represents the objective function of our model, by minimizing the classification cost.

The rest of the paper is organized as follows. In Sect. 2, the ABC algorithm and the VIKOR method are briefly presented. We also describe our proposed hybrid optimization model by adapting the ABC algorithm to be in compliance with the constraints of the problem. Section 3 presents the experimental results and a comparative numerical study with some models from the literature, based on a widely used dataset. We end this paper with a conclusion and discussion regarding future research.

2 The Proposed Work

2.1 Artifical Bee Colony Algorithm

The Artificial Bee Colony optimization algorithm which belongs to the family of evolutionary algorithms is based on a particular intelligent behavior of swarms bees. This approach is inspired by the real behaviors of the bees in their food research and how to share the information on the location of these food sources with other bees from the hive. The method classify the artificial bees into three distinct groups with specific tasks for each category of bees (employed bees, onlookers and scouts). More explicitly, the ABC algorithm is defined by the following steps:

  • Initialization: We begin by generating randomly the initial population in the search space following this equation:

    $$\begin{aligned} u_{j} = x^{min}_{j} + rand[0, 1 ](x^{max}_{j} - x^{min}_{j}) \end{aligned}$$
    (1)

    Where \(x^{min}_{j}\) and \(x^{max}_{j}\) represent the bounds of the search space and \(rand[0, 1 ]\) generates a random number between 0 and 1. Each employed bee evaluate the nectar amount of a food source corresponding to the quality (Fitness) of the associated solution, by:

    $$\begin{aligned} Fitness(i) = \frac{1}{F_{Objective}(i)} \end{aligned}$$
    (2)

    Where \(F_{Objective}\) represents the objective function used in our approch.

  • Moving onlooker bees: The onlookers choose a food source according to the probability value associated with this food source, denoted \(P_{i}\) and calculated by the following expression:

    $$\begin{aligned} P_{i} = \frac{Fitness(i)}{\sum _{n=1}^{SN} Fitness(n)} \end{aligned}$$
    (3)

    where SN is the number of food sources equal to the number of employed bees. The onlooker bee selects a food source and then evaluates its amounts of nectar. Then, the bee moves according to the following formula:

    $$\begin{aligned} v_{ij} = x_{ij} + \phi _{ij} (x_{ij} - x_{kj}) \end{aligned}$$
    (4)

    Where \(k \in [1,2,...,SN]\) and \(j \in [1,2,...,D]\) are randomly chosen indexes. Although k is determined randomly, it has to be different from i. \(\phi _{ij}\) is a random number between \([-1, 1]\). It controls the production of neighbor food sources around \(x_{ij}\).

  • Moving scout bees: If the values of the fitness function of employed bees are not improved for a predetermined number of iterations (Limit), these food sources are abandoned, and the bee that is in this area will move randomly to explore other new food sites, hence the conversion of employed bee to the scout bees. The movement is done by this following equation:

    $$\begin{aligned} v_{ij} = v_{ij}^{min} + rand[0, 1 ](v_{ij}^{max} - v_{ij}^{min}) \end{aligned}$$
    (5)

    At each iteration, the solution having the best value of the Fitness function and the position of the food source found by bees are saved. All these steps are repeated for a predefined number of iterations or until a stopping criterion is satisfied.

2.2 VIKOR

Starting with criteria weights, the VIKOR method operates in order to obtain a compromise ranking-list, as well as the compromise solution, and determines the weight stability intervals for preference stability of the compromise solution. The basic idea of this MCDM method is that the ranking items is based on an index, computed from the measure of “closeness” to the “ideal” solution [23, 26, 32].

We consider that the value of the \(i^{th}\) criterion function for the alternative \(a_{j}\) is denoted \(f_{ij}\) and the alternatives are denoted \(a_{1},a_{2}, ..., a_{J}\), with n as the total number of criteria. \(f^{*}_{i}\) and \(f^{-}_{i}\) represents the best and the worst values of all criterion functions, and B and C represent respectively the sets of benefit and cost criteria. The VIKOR method use the following \(L_{p}-metric\) as an aggregate function:

$$\begin{aligned} L_{p,j}= & {} \left\{ \sum _{i=1}^{n}[(w_{j}(f^{*}_{i} - f_{ij})/ (f^{*}_{i} - f^{-}_{i}) ]^{p}\right\} ^{\frac{1}{p}} 1 \le p \le \infty ; j = 1,2,...,J. \end{aligned}$$
(6)
$$\begin{aligned} f^{*}_{i}= & {} \{(max_{j} \{f_{ij}\} | j \in B, min_{j} \{f_{ij}\} | j \in C)\} \end{aligned}$$
(7)
$$\begin{aligned} f^{-}_{i}= & {} \{(min_{j} \{f_{ij}\} | j \in B, max_{j} \{f_{ij}\} | j \in C)\} \end{aligned}$$
(8)

The next step consists of calculating the three measures S, R and Q (VIKOR Index) of compromise ranking method VIKOR and sort all the alternatives according to these 3 ordered lists:

$$\begin{aligned} S_{j}= & {} \sum _{i=1}^{n} w_{j}(f^{*}_{i} - f_{ij})/ (f^{*}_{i} - f^{-}_{i}) \end{aligned}$$
(9)
$$\begin{aligned} R_{j}= & {} max_{i} \Big [ (w_{j}(f^{*}_{i} - f_{ij})/ (f^{*}_{i} - f^{-}_{i}) \Big ] \end{aligned}$$
(10)
$$\begin{aligned} Q_{j}= & {} v (S_{j} - S^{*}) / (S^{-} - S^{*}) + (1 - v) (R_{j} - R^{*}) / (R^{-} - R^{*}) \nonumber \\ S^{*}= & {} min_{j}~S_{j}, \quad S^{-} = max_{j}~S_{j},\quad R^{*} = min_{j}~R_{j}, \quad R^{-} = max_{j}~R_{j}. \end{aligned}$$
(11)

\(w_{i}\) are the criteria weights and v represents a factor used by the decision maker and reflects the weight of the strategy of “the maximum group utility”. By convention, this factor v is set to 0.5. Once the VIKOR indexes \(Q_{j}\), \(S_{j}\) and \(R_{j}\) are calculated, it only remains to sort all the alternatives in decreasing order of the values S, R and Q, for the purpose of obtaining three ranking lists. The VIKOR algorithm proposes as a compromise solution, for given criteria weights, the alternative (\(a'\)), which is the best ranked by measure Q, if a two conditions are satisfied [26].

2.3 A New Hybrid Approach for ABC MCIC

We present our proposed hybrid approach developed for the ABC MCIC problem. First, we describe the adjustments made to the Artificial Bee Colony algorithm, in order to comply with the constraints of the problem. The ABC algorithm initializes a population of solutions where each solution has D parameters. These parameters are generated respectively according to the Eqs. 1 and 5 and each vector represents a candidate solution for the optimization problem. But, given that the sum of these generated value may be different from 1, we used a generation procedure of initial solutions to adjust these values according to the constraints of VIKOR method, using the following equation:

$$\begin{aligned} x_{i,j} = x_{max} - rand\left[ 0,\Big [x_{max} - \sum _{t=1}^{D} x_{i,t}\Big ]\right] \end{aligned}$$
(12)

This formulation ensures whenever the sum of the solution parameters is equal to 1. When the onlooker bee move (Eq. 4), the mutation operation of ABC algorithm must be adapted, because the values of the generated solution can overflow the search space. To address this ambiguity, we calibrated the values so that the parameters are still within the range of our required search space:

$$\begin{aligned} X_{i,j} = \left\{ \begin{array}{ll} 0 &{} \text{ if } X_{i,j} < 0\\ \\ 1 &{} \text{ if } X_{i,j} > 1\\ \\ X_{i,j} &{} \text{ otherwise. } \end{array} \right. \end{aligned}$$
(13)

This adjustment values can still generate values that their sum is not equal to 1. In this sense, we proceeded to the normalization of the vector to achieve a unitary sum, using the following equation:

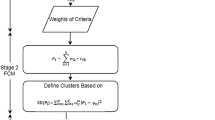
$$\begin{aligned} X_{i,j} = \frac{X_{i,j}}{\sum _{z=1}^{D} X_{i,z}} \end{aligned}$$
(14)

Once these solutions are generated by the ABC algorithm, they will be considered by the VIKOR method as an input parameters, to calculate a score for each item, establish a total ranking items and consequently generate an ABC classification (according to the 20 %–30 %–50 % ABC distribution).

3 Experimental Results

To evaluate the performance of our proposed hybrid approach in the ABC MCIC problem, we consider a data set provided by an Hospital Respiratory Therapy Unit (HRTU). This data set has been widely used in the literature and contains 47 inventory items evaluated in terms of three criteria. This data set is displayed in the Table 1. The ABC classification results of the existing ABC classification models (R model [29], ZF model [33], Chen model [5], H model [11], NG model [25], ZF-NG model [20] and ZF-H model [13]) and our model are showed also in Table 1. Note that all the established classifications respect the same ABC distribtion, with 10 items in the class A, 14 items in the class B and 23 items in the class C. We clearly observe that our proposed approach provides a more efficient classification cost (833.677) than all other models presented from the literature, with a good Fill Rate (0.972) reflecting a good classification.

Table 1. Our approach vs existing classification models
Full size table

4 Conclusions

In this paper, we present a new hybrid approach for ABC MCIC problem. The main contribution of the proposed work is to exploit the efficiency of the ABC algorithm and the method VIKOR on a hybrid manner, to classify the inventory items based on objective weights and to reduce the inventory cost. A comparison has been made between the proposed approach and some existing methods and showed the good performance of the proposed method that outperforms some models from the literature. The idea of combining these two methods in our approach can be easily applied to general multi-criteria classification problems, not just the ABC MCIC problem. To extend this research, it would be interesting to assess the benefits of applying our model empirically using larger datasets.