Abstract
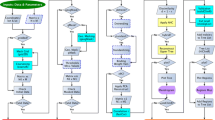
The purpose of this work is to present a new methodology for identifying geographical regions within which the climatic behaviour of a meteorological variable is coherent. We have chosen temperature as the variable of interest, and thermal coherence is defined here in the sense of having a strong (negative) correlation between terrain altitude and temperature. An improved method of constrained spatial cluster analysis is described in the form of a new constrained clustering algorithm. The methodology includes spatial bootstrap statistical tests to provide a more realistic measure of the uncertainty of the coefficient of correlation together with a spatial test of the correlation of residuals. The results are used as optimal estimates of areal temperature averages. The methodology is illustrated by applying it to the annual mean temperature measured at 1220 temperature stations across Spain.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Carrega P (1995) A method for reconstruction of mountain air temperatures with automatic cartographic application. Theor Appl Climatol 52:69–84
DeGaetano AT (2001) Spatial grouping of United States climate stations using a hybrid clustering approach. Int J Climatol 21:791–807
Fereday DR, Knight JR, Scaife AA, Folland CK (2008) Cluster analysis of North Atlantic-European circulation types and links with tropical Pacific sea surface temperatures. J Clim 21:3687–3703
Gerstengarbe F-W, Werner PC, Fraedrich K (1999) Applying non-hierarchical cluster analysis algorithms to climate classification: some problems and their solution. Theor Appl Climatol 64:143–150
Gordon AD (1981) Classification: methods for the exploratory analysis of multivariate data. Chapman and Hall, London. ISBN 0412228505
Gordon AD (1996) A survey of constrained classification. Comput Stat Data Anal 21:17–29
Hoffman FM, Hargrove JR, Erickson DJ, Oglesby RJ (2005) Using clustered climate regimes to analyse and compare predictions from fully coupled general circulation models. Earth Interact 9:1–27
Mahlstein I, Knutti R (2010) Regional climate change patterns identified by cluster analysis. Clim Dyn 35:587–600
Morice CP, Kennedy JJ, Rayner NA, Jones PD (2012) Quantifying uncertainties in global and regional temperature change using an ensemble of observational estimates: the HadCRUT4 data set. J Geophys Res 117:1–22
Robeson SM (1994) Influence of spatial sampling and interpolation on estimates of air temperature change. Clim Res 4:119–126
Stooksbury DE, Michaels PJ (1991) Cluster analysis of South-Eastern U.S. climate stations. Theor Appl Climatol 44(3):143–150
Tang L, Su X, Shao G, Zhang H, Zhao J (2012) Clustering-assisted regression(CAR) approach for developing spatial climate data sets in China. Environ Model Softw 38:122–128
Thacker WC, Lewandowicz R (1997) Partitioning the North Atlantic into regions of similar seasonal sea-surface temperature anomalies. Int J Climatol 17:3–23
Unal Y, Kindap T, Karaca M (2003) Redefining the climate zones of Turkey using cluster analysis. Int J Climatol 23:1045–1055
Viers G (1975) Éléments de climatologie. Fernand Nathan, Paris, 309p
Zhou D, Khan S, Abbas A, Rana T, Zhang H, Chen Y (2009) Climatic regionalisation mapping of the Murrumbidgee irrigation area, Australia. Proc Natl Acad Sci U S A 19:1773–1779
Zscheischler J, Mahecha MD, Harmeling S (2012) Climate classification: the value of unsupervised clustering. Procedia Comp Sci 9:897–906
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this chapter
Cite this chapter
Dowd, P., Wang, H., Pardo-Igúzquiza, E., Yang, Y. (2017). Constrained Spatial Clustering of Climate Variables for Geostatistical Reconstruction of Optimal Time Series and Spatial Fields. In: Gómez-Hernández, J., Rodrigo-Ilarri, J., Rodrigo-Clavero, M., Cassiraga, E., Vargas-Guzmán, J. (eds) Geostatistics Valencia 2016. Quantitative Geology and Geostatistics, vol 19. Springer, Cham. https://doi.org/10.1007/978-3-319-46819-8_61
Download citation
DOI: https://doi.org/10.1007/978-3-319-46819-8_61
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-46818-1
Online ISBN: 978-3-319-46819-8
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)