A Minimal Solution for Non-perspective Pose Estimation from Line Correspondences

Abstract

In this paper, we study and propose solutions to the relatively un-investigated non-perspective pose estimation problem from line correspondences. Specifically, we represent the 2D and 3D line correspondences as Plücker lines and derive the minimal solution for the minimal problem of three line correspondences with Gröbner basis. Our minimal 3-Line algorithm that gives up to eight solutions is well-suited for robust estimation with RANSAC. We show that our algorithm works as a least-squares that takes in more than three line correspondences without any reformulation. In addition, our algorithm does not require initialization in both the minimal 3-Line and least-squares n-Line cases. Furthermore, our algorithm works without a need for reformulation under the special case of perspective pose estimation when all line correspondences are observed from one single camera. We verify our algorithms with both simulated and real-world data.

1 Introduction

Pose estimation is a well-known problem in Computer Vision. It refers to the problem of finding the rigid transformation between a camera frame and a fixed world frame, given a set of 3D structures expressed in the world frame, and its corresponding 2D projections on the camera image. The 2D image projection to 3D structure correspondences can be either points or lines, or less commonly a combination of both. A minimum of three 2D-3D correspondences is needed to solve for the camera pose. Solutions to the pose estimation problem have significant importance in many real-world applications such as robotics localization, visual Simultaneous Localization and Mapping (vSLAM)/Structure-from-Motion (SfM), and augmented reality etc.

The pose estimation problem for a single camera from point or line correspondences is a very well-studied problem, and a huge literature of robust and efficient solutions had been proposed [2, 6, 9, 20, 21, 23, 24, 28] since the 1850s. This problem is also commonly known as the perspective pose estimation problem. In the recent years, due to the increasing popularity of multi-camera systems for robotics applications such as self-driving cars [7, 15, 16, 19] and Micro-Aerial Vehicles [10, 11], many researchers turned their attentions to the so-called non-perspective pose estimation problem [4, 13, 17, 18, 22] from point correspondences. The main difference between the perspective and non-perspective pose estimation problem is that for the latter, light rays casted from the 3D points do not meet at a single point, i.e. there is no single camera center. Consequently, many new algorithms [4, 13, 17, 18, 22] for the non-perspective pose estimation problem from point correspondences were proposed.

Despite the fact that the perspective pose estimation problem from point and line correspondences, and non-perspective pose estimation problem from point correspondences are well-studied, the non-perspective pose estimation problem from line correspondences remains relatively un-investigated. The increasingly wide-spread of multi-camera applications, availability of 3D models from line reconstructions [12], and line detector/descriptor algorithms [8, 27] made the non-perspective pose estimation problem from line correspondences imperatively relevant.

In this paper, we study and propose solutions to the non-perspective pose estimation problem from line correspondences. Specifically, we represent the 2D and 3D line correspondences as Plücker lines and derive the minimal solution for the minimal problem of three line correspondences with Gröbner basis. Our minimal 3-Line algorithm that gives up to eight solutions is well-suited for robust estimation with RANSAC [1]. We show that our algorithm works as a least-squares that takes in more than three line correspondences without any reformulation. In addition, our algorithm does not require initialization in both the minimal 3-Line and least-squares n-Line cases. Furthermore, our algorithm works without a need for reformulation under the special case of perspective pose estimation when all line correspondences are observed from one single camera. We verify our algorithms with both simulated and real-world data.

2 Related Works

It was mentioned in the previous section that to the best of our knowledge no prior work on the non-perspective pose estimation problem from line correspondences exist. Nonetheless, we will discuss some of the relevant existing works on the perspective pose estimation problem from line correspondences in this section.

One of the earliest work on perspective pose estimation from line correspondences was presented by Dhome et al. [6]. They solve the perspective pose estimation problem as a minimal problem that uses three line correspondences. A major disadvantage of their algorithm is that it does not work with more than three line correspondence, which makes it difficult for least-squares estimation in the presence of noise. The fact that their algorithm requires a line to be collinear with the x-axis, and another line to be parallel to the xy-plane made it impossible to extend their work to the non-perspective case.

Ansar and Daniilidis [2] proposed a linear formulation for the perspective pose estimation problem from line correspondences. Their formulation works for four or more line correspondences, but an addition step of Singular Value Decomposition (SVD) is needed for the case of four line correspondences. A problem with [2] is that it resulted in a linear system of equations with 46 variables. The high number of variables compromises the accuracy of the solution [3]. We did not adopt Ansar’s formulation although it is possible to extend the algorithm for the non-perspective pose estimation problem. This is because similar to the perspective case, it results in a linear system of equations with high number of variables. Moreover, the formulation is not minimal, thus not ideal for robust estimation with RANSAC [1].

More recently, Mirzaei et al. [20] proposed an algorithm for perspective pose estimation from three or more line correspondences. They formulated the problem as non-linear least-squares, and solve it as an eigenvalue problem using the Macaulay matrix without a need for initialization. The algorithm yields 27 solutions, and this makes it difficult to identify the correct solution. We do not choose Mirzaei’s formulation despite the fact that it is possible to extend the algorithm for non-perspective pose estimation because of the high number of solutions.

In [28], Zhang et al. proposed an algorithm for perspective pose estimation with three or more line correspondences. In contrast to Mirzaei et al. [20], the algorithm proposed by Zhang et al. is more practical since it yields up to only eight solutions. However, the requirement to align one of the 3D lines with the z-axis of the camera frame made it impossible to extend the algorithm for non-perspective pose estimation.

The most recent work on perspective pose estimation from line correspondences is presented by Pr̆ibyl et al. [23]. They represent the 2D-3D line correspondences as, and proposed a linear algorithm that works with nine or more correspondences. Unfortunately, their algorithm uses high number of correspondences, i.e. nine or more, thus is unsuitable for RANSAC. We adopt their representation of line correspondences as Plücker lines and extend their work to non-perspective pose estimation. Furthermore, we derive the minimal solution for the 3-Line minimal problem that is suitable for RANSAC, and show that our algorithm works without a need for reformulation under the special case of perspective pose estimation when all line correspondences are observed from the same camera.

3 Problem Definition

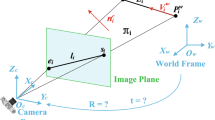
Figure 1 shows an example of a minimal case multi-camera non-perspective pose estimation problem from line correspondences. We are given three 3D lines $L_{W_1}, L_{W_2}, L_{W_3}$ defined in a fixed world frame $F_W$, and its corresponding 2D image projections $l_{c_1}, l_{c_2}, l_{c_3}$ seen respectively by three cameras $F_{C_1}, F_{C_2}, F_{C_3}$. These three cameras are rigidly fixed together, and $F_G$ is the reference frame. We made the assumption that the cameras are fully calibrated, i.e. the camera intrinsics $K_i$ and extrinsics $T^G_{C_i}$ for $i=1,2,3$ are known. Here, $T^G_{C_i}$ is the $4 \times 4$ homogeneous transformation matrix that brings a point defined in $F_{C_i}$ to $F_{G}$. Note that in general, the minimal case for non-perspective pose estimation can be three 2D-3D line correspondences from a multi-camera system made up of either two or three cameras.

Fig. 1.

An example of the non-perspective pose estimation problem from line correspondences.

Definition 1

The non-perspective pose estimation problem seeks to find the pose of the multi-camera system with respect to the fixed world frame, i.e. relative transformation

$$\begin{aligned} T^W_G = \begin{pmatrix} R^W_G &{} t^W_G \\ 0_{3 \times 3} &{} 1 \end{pmatrix} \end{aligned}$$

(1)

that brings a point defined in the multi-camera reference frame $F_G$ to the fixed world frame $F_W$ from the 2D-3D line correspondences $L_{W_j} \leftrightarrow l_{c_j}$, where j is the line correspondence index. We refer to the problem as the Non-Perspective 3-Line (NP3L) or Non-Perspective n-Line problems (NPnL) depending on the number of 2D-3D line correspondences that are used.

4 NP3L: 3-Line Minimal Solution

We represent the 2D-3D line correspondence as a 6-vector Plücker line in our formulation for the non-perspective pose estimation problem. Let us denote $P_a^W = [P_{ax}^W~P_{ay}^W~P_{az}^W~1]^T$ and $P_b^W = [P_{bx}^W~P_{by}^W~P_{bz}^W~1]^T$ as the homogeneous coordinates expressed in the world frame $F_W$ that represent the two end points of the 3D line segment $L_W$. The 6-vector Plücker line of the 3D line segment is given by $L_W = [U_W^T~V_W^T]^T$, where

$$\begin{aligned} V_W = \frac{P_b^W - P_a^W}{\left\| P_b^W - P_a^W \right\| },~~ U_W = P_a^W \times V_W. \end{aligned}$$

(2)

Fig. 2.

A 2D-3D line correspondence represented as Plücker lines.

Geometrically, $V_W$ is the unit direction vector of the 3D line segment, and $U_W$ is the vector that represents the moment of the first 3D line segment end point $P_a^W$ and the unit direction vector $V_W$ as illustrated by Fig. 2. Note that for simplicity, we only show the illustration for one camera and one 2D-3D line correspondence in Fig. 2, and we drop the camera and line indices for brevity. $L_W = [U_W^T~V_W^T]^T$ is known in the non-perspective pose estimation problem and it is expressed in the coordinate frame of the fixed world frame $F_W$.

The Plücker line $L_W$ can be expressed in the camera reference frame $F_C$ as follows:

$$\begin{aligned} L_C = \mathcal {T}_W^CL_W = \begin{pmatrix} R_W^C &{} \lfloor t_W^C \rfloor _{\times } R_W^C \\ 0_{3 \times 3} &{} R_W^C \end{pmatrix}L_W, \end{aligned}$$

(3)

where $\mathcal {T}_W^C$ is the transformation matrix that brings a Plücker line defined in the fixed world frame $F_W$ to the camera reference frame $F_C$. $R_W^C$ and $t_W^C$ are the $3 \times 3$ rotation matrix and $3 \times 1$ translation vector. Specifically,

$$\begin{aligned} T_W^C = \begin{pmatrix} R_W^C &{} t_W^C \\ 0_{1 \times 3} &{} 1 \end{pmatrix} = \begin{pmatrix} R_G^C &{} t_G^C \\ 0_{1 \times 3} &{} 1 \end{pmatrix} \begin{pmatrix} R_W^G &{} t_W^G \\ 0_{1 \times 3} &{} 1 \end{pmatrix} = \begin{pmatrix} R_G^C R_W^G &{} R_G^C t_W^G + t_G^C \\ 0_{1 \times 3} &{} 1 \end{pmatrix}, \end{aligned}$$

(4)

where $(R_G^C,~t_G^C)$ is the known camera extrinsics, and $(R_W^G,~t_W^G)$ is the unknown pose of the multi-camera system defined in the previous section. Since $L_C = [U_C^T~V_C^T]^T$,

$$\begin{aligned} U_C = \begin{pmatrix} R_W^C \; \lfloor t_W^C \rfloor _{\times } R_W^C \end{pmatrix} \begin{pmatrix} U_W \\ V_W \end{pmatrix} \end{aligned}$$

(5)

is a vector defined in $F_C$ that is perpendicular to the plane formed by the projection of the 3D line onto the camera image as shown in Fig. 2, and

$$\begin{aligned} V_C = R_W^C V_W \end{aligned}$$

(6)

is the unit direction vector of the 3D line in the camera reference frame $F_C$.

In addition to the end points $P_a^W$ and $P_b^W$ of the 3D line segment $L_W$, we are also given the image coordinates of the end points $p_a = [p_{ax}~p_{ay}~1]^T$ and $p_b=[p_{bx}~p_{by}~1]^T$ from the 2D image line correspondence $l_C$ of the 3D line. Similar to $L_W$, we can also represent $l_C$ as a Plücker line $[u_C^T~v_C^T]^T$, where

$$\begin{aligned} v_C = \frac{\hat{p}_b - \hat{p}_a}{\left\| \hat{p}_b - \hat{p}_a \right\| },~~ u_C = \hat{p}_a \times v_C. \end{aligned}$$

(7)

$\hat{p}_a = [\hat{p}_{ax}~\hat{p}_{ay}~1]^T = K^{-1}p_a$ and $\hat{p}_b = [\hat{p}_{bx}~\hat{p}_{by}~1]^T = K^{-1}p_b$ are the camera matrix normalized image coordinates. $v_C$ is the unit direction vector of the 2D image line segment, and it is parallel to $V_C$ from Eq. 6. The third element of $v_C$ is always zero since $l_C$ lies on the image plane that is parallel to the xy-plane of $F_C$. $u_C$ is the vector that represents the moment of the first camera matrix normalized 2D image line segment end point $\hat{p}_a$ and the unit direction vector $v_C$ as shown in Fig. 2, and it is parallel to $U_C$ from Eq. 5.

4.1 Solving for $R^G_W$

It is important to note that the moment vector U is always perpendicular to the unit direction vector V in any Plücker line $[U^T~V^T]^T$, i.e. the dot product of U and V must be zero. As a result, we get the following constraint from Eq. 6:

$$\begin{aligned} U_C^T R_W^C V_W = 0. \end{aligned}$$

(8)

Since we know that $u_C$ is parallel to $U_C$, and $R_W^C = R_G^C R_W^G$, we can rewrite Eq. 8 as

$$\begin{aligned} u_C^T R_G^C R_W^G V_W = 0, \end{aligned}$$

(9)

where the only unknown is $R_W^G$. Equation 9 can be rearranged into the form of a homogeneous linear equation $ar = 0$, where a is a $1 \times 9$ matrix made up of the known variables $u_C^T$, $R_G^C$ and $V_W$, and $r = [r_{11}~r_{12}~r_{13}~r_{21}~r_{22}~r_{23}~r_{31}~r_{32}~r_{33}]^T$ is a 9-vector made up the nine entries of the unknown rotation matrix $R_W^G$. Given three 2D-3D line correspondences in the minimal case, we obtain a homogeneous linear equation

$$\begin{aligned} Ar = 0, \end{aligned}$$

(10)

where A is a $3 \times 9$ matrix made up of $a_j$ for $j=1,2,3$. Taking the Singular Value Decomposition (SVD) of the matrix A gives us six vectors denoted by $b_1, b_2, b_3, b_4, b_5, b_6$ that span the right null-space of A. Hence, r is given by

$$\begin{aligned} r = \beta _1b_1 + \beta _2b_2 + \beta _3b_3 + \beta _4b_4 + \beta _5b_5 + \beta _6b_6. \end{aligned}$$

(11)

$\beta _1, \beta _2, \beta _3, \beta _4, \beta _5, \beta _6$ are any scalar values that made up the family of solutions for r. Setting $\beta _6 = 1$, we can solve for $\beta _1, \beta _2, \beta _3, \beta _4, \beta _5$ using the additional constraints from the orthogonality of the rotation matrix $R_W^G$. Following [25], enforcing the orthogonality constraint on the rotation matrix $R_W^G$ gives us 10 constraints:

$$\begin{aligned} ||\mathbf{r_1}||\mathbf{\mathbf{^2}} - ||\mathbf{r_2}||\mathbf{^2} = \mathbf{0},~~ ||\mathbf{r_1}||\mathbf{^2} - ||\mathbf{r_3}||\mathbf{^2} = \mathbf{0},\end{aligned}$$

(12a)

$$\begin{aligned} ||\mathbf{c_1}||\mathbf{^2} - ||\mathbf{c_2}||\mathbf{^2} = \mathbf{0},~~ ||\mathbf{c_1}||\mathbf{^2} - ||\mathbf{c_3}||\mathbf{^2} = \mathbf{0},\end{aligned}$$

(12b)

$$\begin{aligned} \mathbf{r_1} \mathbf{r_2}\mathrm{\mathbf{^T}} = \mathbf{0},~~ \mathbf{r_1} \mathbf{r_3}\mathrm{\mathbf{^T}} = \mathbf{0},~~ \mathbf{r_2} \mathbf{r_3}\mathrm{\mathbf{^T}} = \mathbf{0}, \end{aligned}$$

(12c)

$$\begin{aligned} \mathbf{c_1}\mathrm{\mathbf{^T}} \mathbf{c_2} = \mathbf{0},~~ \mathbf{c_1}\mathrm{\mathbf{^T}} \mathbf{c_3} = \mathbf{0},~~ \mathbf{c_2}\mathrm{\mathbf{^T}} \mathbf{c_3} = \mathbf{0}. \end{aligned}$$

(12d)

Here, $\mathbf{r_j}$ for $j=1,2,3$ and $\mathbf{c_j}$ for $j=1,2,3$ are the rows and columns of the rotation matrix $R_W^G$. Putting r from Eq. 11 into the 10 orthogonality constraints in Eq. 12, we get a system of 10 polynomial equations in terms of $\beta _1, \beta _2, \beta _3, \beta _4, \beta _5$, i.e.

$$\begin{aligned} f_j(\beta _1, \beta _2, \beta _3, \beta _4, \beta _5) = 0,~~~j=1,2...10. \end{aligned}$$

(13)

We use the automatic generator provided by Kukelova et al. [14] to generate the solver for the system of polynomials in Eq. 13. A maximum of up to eight solutions can be obtained. $\beta _1, \beta _2, \beta _3, \beta _4, \beta _5$ are substituted back into Eq. 11 to get the solutions for r that makes up the rotation matrix $R^G_W$. For each of the solutions, we divide $R^G_W$ by the norm of its first row $||\mathbf{r_1}||$ to enforce the orthonormal constraint for a rotation matrix. Furthermore, we ensure that $R^G_W$ follows a right-handed coordinate system by multiplying it with $-1$ if ${det(R^G_W) = -1}$.

4.2 Solving for $t_W^G$

It was mentioned earlier that $u_C$ is the vector that represents the moment of the first camera matrix normalized 2D image line segment end point $\hat{p}_a$ and the unit direction vector $v_C$ as shown in Fig. 2, and it is parallel to $U_C$ from Eq. 4. This means that we can write

$$\begin{aligned} \lambda u_C = U_C, \end{aligned}$$

(14)

where $\lambda$ is a scalar value. Substituting Eq. 14 into Eq. 5, we get

$$\begin{aligned} \lambda u_C = \begin{pmatrix} R_W^C \; \lfloor t_W^C \rfloor _{\times } R_W^C \end{pmatrix} \begin{pmatrix} U_W \\ V_W \end{pmatrix}. \end{aligned}$$

(15)

$[R_W^C~~\lfloor t_W^C \rfloor _{\times } R_W^C]$ can be seen as a $3 \times 6$ projection matrix that projects a 3D Plücker line $[U_W^T~V_W^T]^T$ onto a 2D image. It can be easily seen from Fig. 2 that $\lambda u_C$ is the normal vector of the plane formed by the projection of the 3D Plücker line $[U_W^T~V_W^T]^T$ onto the image plane.

Taking the cross product of $u_C$ on both sides of Eq. 15 to get rid of the unknown $\lambda$, we get

$$\begin{aligned} \left\lfloor u_C \right\rfloor _{\times } \begin{pmatrix} R_W^C \; \lfloor t_W^C \rfloor _{\times } R_W^C \end{pmatrix} \begin{pmatrix} U_W \\ V_W \end{pmatrix} = 0. \end{aligned}$$

(16)

We substitute the known camera extrinsics $(R_G^C, t_G^C)$ and rotation matrix $R^G_W$ that we solved in Sect. 4.1 into Eq. 16 to get two constraints with the unknown translation $t_W^G$ for each 2D-3D line correspondence $u_C \leftrightarrow [U_W^T~V_W^T]^T$:

$$\begin{aligned} \left\lfloor u_C \right\rfloor _{\times } \begin{pmatrix} R_G^C R^G_W \; \lfloor R_G^C t_W^G + t_G^C \rfloor _{\times } R_G^C R^G_W \end{pmatrix} \begin{pmatrix} U_W \\ V_W \end{pmatrix} = 0. \end{aligned}$$

(17)

Equation 17 can be rearranged into a homogeneous linear equation $bt = 0$, where b is a $2 \times 4$ matrix made up of all the known variables $R_G^C, t_G^C, R^G_W, u_C, U_W$ and $V_W$, and $t = [t_x~t_y~t_z~1]^T$ is a 4-vector made up of the three entries of the unknown translation vector $t_W^G$. Given three 2D-3D line correspondences in the minimal case, we obtain a overdetermined homogeneous linear equation

$$\begin{aligned} Bt = 0. \end{aligned}$$

(18)

B is a $6 \times 4$ matrix made up of $b_j$ for $j=1,2,3$. We solve for t by taking the 4-vector that spans the right null-space of B. The final solution is obtained by dividing the 4-vector with its last element since $t = [t_x~t_y~t_z~1]^T$. Finally, $t_W^G$ is the first three elements of t.

We get up to eight solutions for the unknown pose $(R_W^G, t_W^G)$ of the world frame $F_W$ to the multi-camera system $F_G$. We use each of the solution to transform the end points $P_a^W$ and $P_b^W$ from each of the 3D line into the camera frame $F_C$, and retain the solutions that give the most number of lines with at least one end point from each line that appears in front of the camera, i.e. $P_{az}^C > 0$ or $P_{bz}^C > 0$. Finally, the correct solution can be identified from the reprojection errors (see Sect. 6 for the details of reprojection errors) for all the other 2D-3D line correspondences. A 2D-3D line correspondence is chosen as an inlier if the reprojection error is lesser than a pre-defined threshold, and the correct solution is chosen as the one that yields the most number of inliers.

5 NPnL: $\ge$3 Line Correspondences

In general, the solution steps remain unchanged for $n\ge 3$ 2D-3D line correspondences. The system of homogeneous linear equations $Ar=0$ from Eq. 10 is valid for $n\ge 3$ 2D-3D line correspondences, i.e. A is a $n \times 9$ matrix where $n\ge 3$. Similar to the minimal case, we can find six vectors $b_1, b_2, b_3, b_4, b_5, b_6$ that spans the right null-space of A using SVD, where $b_6$ is set to 1. The solution for $R_W^G$ is obtained by enforcing the orthogonality constraints in Eq. 12. We get up to eight solutions for $R_W^G$. For each solution of $R_W^G$, we solve for $t_W^G$ following the steps described in Sect. 4.2. $Bt=0$ from Eq. 18 is now a $2n \times 4$ matrix, where $n\ge 3$. Solutions that give the most number of lines with at least one end point from each line that appears in front of the camera are retained. The final solution for $(R_W^G, t_W^G)$ is chosen to be the one with the highest number of inliers.

6 Reprojection Error for RANSAC

Figure 3 shows an illustration of the reprojection error that we use to reject outliers within RANSAC, and to determine the correct solution for the pose of the multi-camera system. For each estimated pose $(R_W^G, t_W^G)$, we transform the 3D end points ($P_a^W$, $P_b^W$) defined in the world frame $F_W$ into the camera frame $F_C$ as follows:

$$\begin{aligned} P_k^C = \begin{pmatrix} R_G^C R_W^G &{} R_G^C t_W^G + t_G^C \\ 0_{1 \times 3} &{} 1 \end{pmatrix} P_k^W,~~~~k=a,b, \end{aligned}$$

(19)

where ($R_G^C$, $t_G^C$) is the known camera extrinsics. Next, we compute the reprojection of $P_a^C$ and $P_b^C$ onto the image:

Fig. 3.

An illustration of reprojection error from a 2D-3D line correspondence.

$$\begin{aligned} \tilde{p}_k = K P_k^C,~~~~ \tilde{p}_k = \frac{\tilde{p}_k}{\tilde{p}_{kz}},~~~~k=a,b, \end{aligned}$$

(20)

where K is the camera intrinsics. Note that the division by $\tilde{p}_{kz}$ is to ensure that $\tilde{p}_a$ and $\tilde{p}_b$ are homogeneous coordinates. The reprojection error e is then computed as the mean of the shortest distances $d_a$ and $d_b$ from the camera matrix normalized 2D line end points $\hat{p}_a$ and $\hat{p}_b$ to the infinite line formed by the camera matrix normalized reprojected correspondence line end points $K^{-1}\tilde{p}_a$ and $K^{-1}\tilde{p}_b$. We remove the influence from the length of the line segment by normalizing the reprojection error with the distance between $\hat{p}_a$ and $\hat{p}_b$. Specifically,

$$\begin{aligned} e = \frac{d_a + d_b}{2(\left\| \hat{p}_b - \hat{p}_a \right\| )}. \end{aligned}$$

(21)

Any 2D-3D line correspondence with $e \ge \alpha$, where $\alpha$ is a pre-defined threshold is rejected as an outlier.

7 Special Cases

One Camera: The problem becomes the perspective pose estimation problem with line correspondences when all correspondences are seen by only one camera. Here the camera extrinsics ($R_G^C$, $t_G^C$) from Eq. 4 vanishes, and we directly solve for the camera orientation $R_W^C$ from Eq. 8 without the need to decompose the orientation into $R_G^C R_W^G$. Similarly, we can solve for the camera translation $t_W^C$ directly from Eq. 16. The steps for solving the single camera pose from $\ge 3$ line correspondences remain the same as described in Sect. 5.

Parallel 3D Lines: This is the minimal case where two or all the three 3D lines are parallel. Since the unit directions $V_W$ from Eq. 8 are the same for parallel lines, the rank of matrix A from Eq. 10 drops below 3. Consequently, $R^G_W$ from Sect. 4.1 cannot be solved. Fortunately, we can easily prevent this degenerate case by omitting parallel lines.

8 Results

We validate our non-perspective pose estimation algorithm with line correspondences from both simulated and real-world datasets. Our algorithm is implemented on Matlab and takes $\sim 0.07$ s to solve for the solution. Note that due to the absence of prior methods for non-perspective pose estimation from line correspondences as comparisons, we focus our evaluations on the stability and accuracy of our algorithm based on different configurations of the multi-camera system. In addition, we also do a comparison of our algorithm under the special case of one camera with the existing methods from Zhang et al. [28] and Mirzaei et al. [20].

8.1 Simulations

One Line Per Camera: We first evaluate the accuracy of our algorithm for different number of cameras in the multi-camera system. We randomly generate 500 different multi-camera poses $T^W_{G}$ uniformly drawn from a range of $[-5,5]$ m and $[-1,1]$ rad for all x, y, z axes, and roll, pitch and yaw angles. For each of these multi-camera pose, we randomly generate the extrinsics $T^G_{C_i}$, for $i=3,10,50,100$ cameras. All the cameras all generated to lie on a sphere centered on the multi-camera frame $F_G$ with their z-axis pointing outwards. Hence, the extrinsics $T^G_{C_i}$ are uniformly drawn from a sphere radius range of [1, 5] m with the xy-plane orientation on the sphere uniformly drawn from a range of $[-\pi ,\pi ]$ rad. We randomly generate one 2D line for each camera, where the line end points are uniformly drawn within the range of the image width and height. We fixed the image size at $1280 \times 1024$. Only 2D lines with length more than 30 pixels are accepted. The depths that correspond to the end points of the 2D image lines are uniformly drawn from a range of [5, 10] m.

Fig. 4.

Comparisons of the average relative (a) rotational and (b) translational errors for 3, 10, 50 and 100 cameras with 1 line correspondence per camera. Note that the configuration with 3 cameras is the minimal case. (Color figure online)

Figure 4 shows the plots of the average relative rotational and translational errors for 3, 10, 50, 100 cameras with one line per camera, where the end points of the 2D image lines are corrupted by noise that follows an uniform distribution with variance of 1 to 20 pixels at a step size of 1 pixel centered around the original end point values. Following [24], the relative translational error is computed as $\frac{2(||\tilde{t}-t||)}{||\tilde{t}||+||t||}$, where $\tilde{t}$ and t is the ground truth and estimated translations. The relative rotational error is computed as the norm of the Euler angles from $\tilde{R}^TR$, where $\tilde{R}$ and R are the ground truth and estimated rotation matrices. We can observe from Fig. 4 that the rotational and translational errors is the highest for the minimal case (shown in green) and decreases with increasing number of cameras. We can also see that the errors remain small with increasing noise.

Ten Cameras: Figure 5 shows the comparisons of the average relative rotational and translational errors for 500 randomly generated multi-camera system with 10 cameras, where each camera sees 1, 10, 50, 100 lines with the end points corrupted with noise from 1 to 20 pixels at a step size of 1 pixel. We can see that the errors for the 1 line per camera case (shown in green) is the highest, and decrease gradually for the 10, 50, 100 lines per camera cases. Overall, the errors increase but remain small with increasing pixel noise.

Fig. 5.

Comparisons of the average relative (a) rotational and (b) translational errors for 1, 10, 50 and 100 lines per camera with 10 cameras. (Color figure online)

One Camera: Figure 6 shows the comparisons of the average rotational and translational errors from our algorithm, [20, 28] for 500 randomly generated single cameras, where the end points of the 2D image lines are corrupted with noise from 1 to 20 pixels at a step size of 1 pixel. The number of lines seen by the camera vary from 3 (our), 4 [20, 28], 10, 50 and 100. It is the minimal case when the number of lines is 3. Note that no results from the minimal case are shown for [20, 28] since the open-source Matlab codes are implemented for $\ge 4$ line correspondences. Despite the fact the our algorithm is formulated for non-perspective pose estimation, it can be observed from Fig. 6 that our algorithm shows similar accuracy as [20, 28] under the influence of noise for perspective pose estimation without a need for reformulation.

Fig. 6.

Comparisons of the average relative (a) rotational and (b) translational errors from our algorithm, [20, 28] for 3 (our), 4 [20, 28], 10, 50 and 100 lines in one camera. Note that the configuration with 3 lines in one camera is the minimal case for our algorithm.

8.2 Real-World Data

We test the accuracy of our non-perspective pose estimation algorithm with the 3D line models shown in Figs. 7 and 8. The 3D line models are reconstructed from 113 (Dataset 01) and 229 (Dataset 02) images respectively. We first do a 3D reconstruction with [26] to get the camera poses (shown in red) and sparse 3D points of the structures. Next, we discard the 3D points and use the camera poses to compute the 3D lines of the structures (shown in blue) using [12]. In our experiments, we emulate a multi-camera system by randomly selecting $\ge 3$ cameras from the cameras in the 3D models. One of the selected cameras is chosen to be the reference frame of the multi-camera system. The ground truth pose of the multi-camera system, i.e. pose of the reference frame, and the extrinsics of the other cameras in the multi-camera system are computed with the known poses from the 3D reconstruction. The camera poses shown in green from Figs. 7 and 8 are examples of the emulated multi-camera system. The images shown on the left of the 3D line models are the images seen by the selected multi-camera system shown in green. For each emulated multi-camera system, we remove the cameras from the 3D model, find the 2D-3D line correspondences, and compute the pose of the multi-camera system with our non-perspective pose estimation algorithm. The estimated pose is then compared with the ground truth, i.e. pose of the reference frame for evaluation.

Fig. 7.

3D Line model from Dataset 01 (113 images) for testing our non-perspective pose estimation algorithm. (Color figure online)

Fig. 8.

3D Line model from Dataset 02 [5] (229 images) for testing our non-perspective pose estimation algorithm. (Color figure online)

Table 1 shows the comparisons of the average relative rotational and translational errors from our non-perspective pose estimation algorithm with multi-camera systems that are made up of 3, 5, 10, 20, 25 cameras from both Dataset 01 and 02 respectively. For each multi-camera system, the average rotational and translational errors are computed from 80 sets of randomly selected cameras. We can see that the average errors for both datasets remain low and stable for the different number of cameras in the multi-camera system.

Table 1. Average relative rotational (R Error, Radian) and translational (t Error, No Units) errors for multi-camera systems emulated with 3, 5, 10, 20 and 25 cameras from datasets 01 and 02 respectively.

Table 2. Comparisons of the average relative rotational (R Error, Radian) and translational (t Error, No Units) errors from our algorithm, and [20, 28] for one camera.

Table 2 shows the comparisons of the average relative rotational and translational errors from our algorithm, [20, 28] for the special case of one camera. The average relative rotational and translational errors are computed from 80 randomly selected cameras. We can see that the average errors from our algorithm are small and comparable to [20, 28]. Note that RANSAC is used to eliminate outliers for all the algorithms.

9 Conclusions

We derived the minimal solution for the relatively un-investigated minimal problem of non-perspective pose estimation from line correspondences. We showed that our minimal 3-Line algorithm gives up to eight solutions, and is well-suited for robust estimation with RANSAC. Our algorithm works as a least-squares that takes in more than three line correspondences without any reformulation. In addition, our algorithm does not require initialization in both the minimal 3-Line and least-squares n-Line cases. We further showed that our algorithm works without any need for reformulation under the special case of perspective pose estimation when all line correspondences are observed from one single camera. We verified our algorithms with both simulated and real-world data.