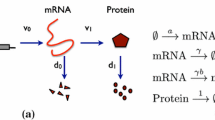
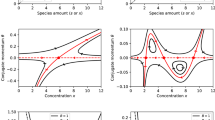
Abstract
The stochastic nature of chemical reactions has resulted in an increasing research interest in discrete-state stochastic models and their analysis. A widely used approach is the description of the temporal evolution of such systems in terms of a chemical master equation (CME). In this paper we study two approaches for approximating the underlying probability distributions of the CME. The first approach is based on an integration of the statistical moments and the reconstruction of the distribution based on the maximum entropy principle. The second approach relies on an analytical approximation of the probability distribution of the CME using the system size expansion, considering higher order terms than the linear noise approximation. We consider gene expression networks with unimodal and multimodal protein distributions to compare the accuracy of the two approaches. We find that both methods provide accurate approximations to the distributions of the CME while having different benefits and limitations in applications.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
Noncentral moments can be easily obtained from central ones. For instance, the second noncentral moment \(\mu ^{(2)}\) is obtained from the variance \(\sigma ^2\) and the mean \(\mu \) as \(\mu ^{(2)} = \sigma ^2 + \mu ^2\).
References
H. H. McAdams and A. Arkin.: “Stochastic mechanisms in gene expression”. Proc Natl Acad Sci 94.3 (1997), pp. 814–819.
P. S. Swain, M. B. Elowitz, and E. D. Siggia.: “Intrinsic and extrinsic contributions to stochasticity in gene expression”. Proc Natl Acad Sci 99.20 (2002), pp. 12795–12800.
T. J. Perkins and P. S. Swain.: “Strategies for cellular decision-making”. Mol Syst Biol 5 (2009).
M. B. Elowitz et al.: “Stochastic gene expression in a single cell”. Sci Signal 297.5584 (2002), p. 1183.
D. Wilkinson.: Stochastic Modelling for Systems Biology. Chapman & Hall, 2006.
D. T. Gillespie.: “Exact stochastic simulation of coupled chemical reactions”. J Phys Chem 81.25 (1977), pp. 2340–2361.
N. Maheshri and E. K. O’Shea.: “Living with noisy genes: how cells function reliably with inherent variability in gene expression”. Annu Rev Biophys Biomol Struct 36 (2007), pp. 413–434.
B. Munsky and M. Khammash.: “The finite state projection algorithm for the solution of the chemical master equation”. J Chem Phys 124.4 (2006), p. 044104.
M. Mateescu et al.: “Fast Adaptive Uniformisation of the Chemical Master Equation”. IET Syst Biol 4.6 (2010), pp. 441–452.
D. T. Gillespie.: “Stochastic simulation of chemical kinetics”. Annu Rev Phys Chem 58 (2007), pp. 35–55.
J. Elf and M. Ehrenberg.: “Fast evaluation of fluctuations in biochemical networks with the linear noise approximation”. Genome Res 13.11 (2003), pp. 2475–2484.
R Grima. “An effective rate equation approach to reaction kinetics in small volumes: Theory and application to biochemical reactions in nonequilibrium steady-state conditions”. J Chem Phys 133.3 (2010), p. 035101.
P. Thomas, H. Matuschek, and R. Grima.: “How reliable is the linear noise approximation of gene regulatory networks?” BMC Genomics 14. Suppl 4 (2013), S5.
S. Engblom.: “Computing the moments of high dimensional solutions of the master equation”. Appl Math Comput 180 (2 2006), pp. 498 -515.
C. Gillespie. “Moment-closure approximations for mass-action models”. IET Syst Biol 3.1 (2009), pp. 52–58.
A. Ale, P. Kirk, and M. P. H. Stumpf.: “A general moment expansion method for stochastic kinetic models”. J Chem Phys 138.17 (2013), p. 174101.
A. Andreychenko, L. Mikeev, and V.Wolf.: “Model Reconstruction for Moment-Based Stochastic Chemical Kinetics”. ACM Trans Model Comput Simul 25.2 (2015), 12:1–12:19.
A. Andreychenko, L. Mikeev, and V. Wolf.: “Reconstruction of Multimodal Distributions for Hybrid Moment-based Chemical Kinetics”. To appear in Journal of Coupled Systems and Multiscale Dynamics (2015).
N. G. Van Kampen.: Stochastic Processes in Physics and Chemistry. Third. Amsterdam: Elsevier, Amsterdam, 1997.
P. Thomas and R. Grima. : “Approximate probability distributions of the master equation”. Phys Rev E 92.1 (2015), p. 012120.
L. Bortolussi.: “Hybrid Behaviour of Markov Population Models”. Information and Computation (2015 (accepted)).
P. Thomas, N. Popović, and R. Grima.: “Phenotypic switching in gene regulatory networks”. Proc Natl Acad Sci 111.19 (2014), pp. 6994–6999.
D. T. Gillespie: “A diffusional bimolecular propensity function”. J Chem Phys 131.16 (2009), p. 164109.
P. Thomas, H. Matuschek, and R. Grima.: “Computation of biochemical pathway fluctuations beyond the linear noise approximation using iNA”. Bioinformatics and Biomedicine (BIBM), 2012 IEEE International Conference on. IEEE. 2012, pp. 1–5.
P. Whittle.: “On the Use of the Normal Approximation in the Treatment of Stochastic Processes”. J R Stat Soc Series B Stat Methodol 19.2 (1957), pp. 268–281.
J. H. Matis and T. R. Kiffe.: “On interacting bee/mite populations: a stochastic model with analysis using cumulant truncation”. Environ Ecol Stat 9.3 (2002), pp. 237–258.
I. Krishnarajah et al.: “Novel moment closure approximations in stochastic epidemics”. Bull Math Biol 67.4 (2005), pp. 855–873.
A. Singh and J. P. Hespanha.: “Lognormal moment closures for biochemical reactions”. Decision and Control, 2006 45th IEEE Conference on. IEEE. 2006, pp. 2063–2068.
A. Singh and J. P. Hespanha.: “Approximate moment dynamics for chemically reacting systems”. Automatic Control, IEEE Transactions on 56.2 (2011), pp. 414–418.
D. Schnoerr, G. Sanguinetti, and R. Grima.: “Comparison of different momentclosure approximations for stochastic chemical kinetics”. J Chem Phys 143.18 (2015), p. 185101.
D. Schnoerr, G. Sanguinetti, and R. Grima.: “Validity conditions for moment closure approximations in stochastic chemical kinetics”. J Chem Phys 141.8 (2014), p. 084103.
R. Grima.: “A study of the accuracy of moment-closure approximations for stochastic chemical kinetics”. J Chem Phys 136.15 (2012), p. 154105.
J. Hasenauer et al.: “Method of conditional moments for the Chemical Master Equation”. J Math Biol (2013), pp. 1–49.
M. Lapin, L. Mikeev, and V. Wolf.: “SHAVE - Stochastic Hybrid Analysis of Markov Population Models”. Proceedings of the 14th International Conference on Hybrid Systems: Computation and Control (HSCC’11). ACM International Conference Proceeding Series. 2011.
A.L. Berger, V.J.D. Pietra, S.A.D. Pietra, A Maximum Entropy Approach to Natural Language Processing. Comput Ling 22(1), 39–71 (1996)
R. Abramov.: “The multidimensional maximum entropy moment problem: a review of numerical methods”. Commun Math Sci 8.2 (2010), pp. 377–392.
Z. Wu et al.: “A fast Newton algorithm for entropy maximization in phase determination”. SIAM Rev 43.4 (2001), pp. 623–642.
L. R. Mead and N. Papanicolaou: “Maximum entropy in the problem of moments”. J Math Phys 25 (1984), p. 2404.
G. W. Alldredge et al.: “Adaptive change of basis in entropy-based moment closures for linear kinetic equations”. J Comput Phys 258 (2014), pp. 489–508.
Á . Tari, M. Telek, and P. Buchholz.: “A unified approach to the moments based distribution estimation-unbounded support”. Formal Techniques for Computer Systems and Business Processes. Springer, 2005, pp. 79–93.
J. Elf et al.: “Mesoscopic kinetics and its applications in protein synthesis”. Systems Biology. Springer, 2005, pp. 95–18.
L. Comtet.: Advanced Combinatorics: The art of finite and infinite expansions. Springer Science & Business Media, 1974.
E. Giampieri et al.: “Active Degradation Explains the Distribution of Nuclear Proteins during Cellular Senescence”. PloS one 10.6 (2015), e0118442.
V. Shahrezaei and P. S. Swain.: “Analytical distributions for stochastic gene expression”. Proc Natl Acad Sci 105.45 (2008), pp. 17256–17261.
P. Thomas, A. V. Straube, and R. Grima.: “Communication: Limitations of the stochastic quasi-steady-state approximation in open biochemical reaction networks”. J Chem Phys 135(18), 181103 (2011)
K. R. Sanft, D. T. Gillespie, and L. R. Petzold.: “Legitimacy of the stochastic Michaelis-Menten approximation”. Syst Biol, IET 5.1 (2011), pp. 58–69.
D. A. Levin, Y. Peres, and E. L. Wilmer.: Markov chains and mixing times. American Mathematical Soc., 2009.
T. M. Cover and J. A. Thomas.: Elements of information theory. John Wiley & Sons, 2012.
Acknowledgements
PT acknowledges support from the Royal Commission for the Exhibition of 1851 in form of a Research Fellowship.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Andreychenko, A., Bortolussi, L., Grima, R., Thomas, P., Wolf, V. (2017). Distribution Approximations for the Chemical Master Equation: Comparison of the Method of Moments and the System Size Expansion. In: Graw, F., Matthäus, F., Pahle, J. (eds) Modeling Cellular Systems. Contributions in Mathematical and Computational Sciences, vol 11. Springer, Cham. https://doi.org/10.1007/978-3-319-45833-5_2
Download citation
DOI: https://doi.org/10.1007/978-3-319-45833-5_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-45831-1
Online ISBN: 978-3-319-45833-5
eBook Packages: EngineeringEngineering (R0)