Abstract
This paper presents an encoding of a non-temporal fragment of the \({\textsc {TLA}} ^{{+}}\) language, which includes untyped set theory, functions, arithmetic expressions, and Hilbert’s \(\varepsilon \) operator, into many-sorted first-order logic, the input language of state-of-the-art smt solvers. This translation, based on encoding techniques such as boolification, injection of unsorted expressions into sorted languages, term rewriting, and abstraction, is the core component of a back-end prover based on smt solvers for the \({\textsc {TLA}} ^{{+}}\) Proof System.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
Non-temporal reasoning is enough for proving safety properties and makes up the vast majority of proof steps in liveness proofs.
- 2.
In this paper we use the terms type and sort interchangeably.
- 3.
\({\textsc {TLA}} ^{{+}}\) operator symbols correspond to the standard function and predicate symbols of first-order logic but we reserve the term “function” for \({\textsc {TLA}} ^{{+}}\) functional values.
- 4.
Both axioms (2.6) and (2.7) for set comprehension objects are instances of the standard axiom schema of replacement: taking the two single-valued predicates
 and
and  , we can define
, we can define  and
and  . The replacement axiom says that, given an expression S and a binary predicate \(\phi \), such that \(\phi \) is single-valued for any x in S, that is, \( \forall x \in S :\forall y,z :\phi (x,y) \wedge \phi (x,z) \Rightarrow y = z, \) then there exists a set object \(\mathcal {R}(S,\phi )\), and that \(x \in \mathcal {R}(S,\phi ) \Leftrightarrow \exists y \in S : \phi (x,y)\).
. The replacement axiom says that, given an expression S and a binary predicate \(\phi \), such that \(\phi \) is single-valued for any x in S, that is, \( \forall x \in S :\forall y,z :\phi (x,y) \wedge \phi (x,z) \Rightarrow y = z, \) then there exists a set object \(\mathcal {R}(S,\phi )\), and that \(x \in \mathcal {R}(S,\phi ) \Leftrightarrow \exists y \in S : \phi (x,y)\). - 5.
The standard semantics of \({\textsc {TLA}} ^{{+}}\) offers three alternatives to interpret expressions [10, Sect. 16.1.3]. In the liberal interpretation, an expression like \(42 \Rightarrow \{\}\) always has a truth value, but it is not specified if that value is true or false. In the conservative and moderate interpretations, the value of \(42 \Rightarrow \{\}\) is completely unspecified. Only in the moderate and liberal interpretation, the expression \(\textsc {false}\Rightarrow \{\}\) has a Boolean value, and that value is true. In the liberal interpretation, all the ordinary laws of logic, such as commutativity of \(\wedge \), are valid, even for non-Boolean arguments.
- 6.
The typical injectivity axiom \( \forall m^\mathsf {Int},n^\mathsf {Int}:\mathsf {i2u} (m) = \mathsf {i2u} (n) \Rightarrow m = n \) generates instantiation patterns for every pair of occurrences of \(\mathsf {i2u}\). Noting that \(\mathsf {i2u}\) is injective iff it has a partial inverse \(\mathsf {u2i}\), we use instead the axiom \( \forall n^\mathsf {Int}:\mathsf {u2i} (\mathsf {i2u} (n)) = n, \) which generates a linear number of \(\mathsf {i2u} (n)\) instances, where \(\mathsf {u2i}: \mathsf {U} \rightarrow \mathsf {Int}\) is unspecified.
- 7.
This encoding does not allow us to implement the standard \({\textsc {TLA}} ^{{+}}\) interpretation of strings, which are considered as tuples of characters. Fortunately, characters are hardly used in practice.
References
Baader, F., Nipkow, T.: Term rewriting and all that. Cambridge University Press, Cambridge (1999)
C. Barrett, A. Stump, and C. Tinelli. The Satisfiability Modulo Theories Library (SMT-LIB)(2010). www.SMT-LIB.org
Blanchette, J.C., Böhme, S., Paulson, L.C.: Extending Sledgehammer with SMT solvers. J Autom. Reasoning 51(1), 109–128 (2013)
Cousineau, D., Doligez, D., Lamport, L., Merz, S., Ricketts, D., Vanzetto, H.: TLA\(^{+}\) proofs. In: Giannakopoulou, D., Méry, D. (eds.) FM 2012. LNCS, vol. 7436, pp. 147–154. Springer, Heidelberg (2012)
Déharbe, D., Fontaine, P., Guyot, Y., Voisin, L.: SMT solvers for Rodin. In: Derrick, J., Fitzgerald, J., Gnesi, S., Khurshid, S., Leuschel, M., Reeves, S., Riccobene, E. (eds.) ABZ 2012. LNCS, vol. 7316, pp. 194–207. Springer, Heidelberg (2012)
Delahaye, D., Doligez, D., Gilbert, F., Halmagrand, P., Hermant, O.: Zenon Modulo: when Achilles Outruns the tortoise using deduction modulo. In: McMillan, K., Middeldorp, A., Voronkov, A. (eds.) LPAR-19 2013. LNCS, vol. 8312, pp. 274–290. Springer, Heidelberg (2013)
Douceur, J.R., Lorch, J.R., Parno, B., Mickens, J., McCune, J.M.: Memoir-Formal Specs and Correctness Proofs. Technical report MSR-TR–19, Microsoft Research (2011)
Hansen, D., Leuschel, M.: Translating TLA\(^{+}\) to B for validation with ProB. In: Derrick, J., Gnesi, S., Latella, D., Treharne, H. (eds.) IFM 2012. LNCS, vol. 7321, pp. 24–38. Springer, Heidelberg (2012)
Konrad, M., Voisin, L.: Translation from set-theory to predicate calculus. Technical report, ETH Zurich (2012)
Lamport, L.: Specifying Systems: The TLA\(^{+}\) Language and Tools for Hardware and Software Engineers. Addison-Wesley, Boston (2002)
Manzano, M.: Extensions of First-Order Logic. Cambridge Tracts in Theoretical Computer Science, 2nd edn. Cambridge University Press, Cambridge (2005)
Mentré, D., Marché, C., Filliâtre, J.-C., Asuka, M.: Discharging proof obligations from Atelier B using multiple automated provers. In: Derrick, J., Fitzgerald, J., Gnesi, S., Khurshid, S., Leuschel, M., Reeves, S., Riccobene, E. (eds.) ABZ 2012. LNCS, vol. 7316, pp. 238–251. Springer, Heidelberg (2012)
Merz, S., Vanzetto, H.: Automatic verification of TLA\(^{+}\) proof obligations with SMT solvers. In: Bjørner, N., Voronkov, A. (eds.) LPAR-18 2012. LNCS, vol. 7180, pp. 289–303. Springer, Heidelberg (2012)
Merz, S., Vanzetto, H.: Harnessing SMT Solvers for TLA\(^{+}\) Proofs. Electron. Commun. Eur. Assoc. Softw. Sci. Tech., 53 (2012)
Merz, S., Vanzetto, H.: Refinement types for tla \(^{+}\). In: Badger, J.M., Rozier, K.Y. (eds.) NFM 2014. LNCS, vol. 8430, pp. 143–157. Springer, Heidelberg (2014)
Plagge, D., Leuschel, M.: Validating B,Z and TLA \(^{+}\) Using ProB and Kodkod. In: Giannakopoulou, D., Méry, D. (eds.) FM 2012. LNCS, vol. 7436, pp. 372–386. Springer, Heidelberg (2012)
Sutcliffe, G.: The TPTP problem library and associated infrastructure. J. Autom. Reason. 43(4), 337–362 (2009)
Urban, J.: Translating Mizar for first-order theorem. In: Asperti, A., Buchberger, B., Davenport, J.H. (eds.) MKM 2003. LNCS, vol. 2594, pp. 203–215. Springer, Heidelberg (2003)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this paper
Cite this paper
Merz, S., Vanzetto, H. (2016). Encoding TLA\(^{+}\) into Many-Sorted First-Order Logic. In: Butler, M., Schewe, KD., Mashkoor, A., Biro, M. (eds) Abstract State Machines, Alloy, B, TLA, VDM, and Z. ABZ 2016. Lecture Notes in Computer Science(), vol 9675. Springer, Cham. https://doi.org/10.1007/978-3-319-33600-8_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-33600-8_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-33599-5
Online ISBN: 978-3-319-33600-8
eBook Packages: Computer ScienceComputer Science (R0)


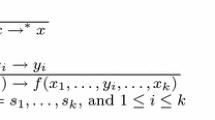


 and
and  , we can define
, we can define  and
and  . The replacement axiom says that, given an expression S and a binary predicate
. The replacement axiom says that, given an expression S and a binary predicate