A Variational Approach for Mean-Variance-Optimal Deterministic Consumption and Investment

Abstract

A significant number of life insurance contracts are based on deterministic investment strategies—this justifies to restrict the set of admissible controls to deterministic controls. Optimal deterministic controls can be identified by Hamilton-Jacobi-Bellman techniques, but for the corresponding partial differential equations only numerical solutions are available and so the general existence of optimal controls is unclear. We present a non-constructive existence result and derive necessary characterizations for optimal controls by using a Pontryagin maximum principle. Furthermore, based on the variational idea of the Pontryagin maximum principle, we derive a numerical optimization algorithm for the calculation of optimal controls.

Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Among many other applications, individual investment strategies arise in pension saving contracts, see for example Cairns [6]. While in dynamic optimal consumption-investment problems one typically aims to find an optimal control from the set of adapted processes, in insurance practice quite a number of contracts rely on deterministic investment strategies. Deterministic investment and consumption strategies have the advantage that they are easier to organize in asset management, that they make future consumption predictable, and that they are easier to communicate. From a mathematical point of view, deterministic control avoids unwanted features of stochastic control such as diffusive consumption, satisfaction points and consistency problems. For further arguments and a detailed comparison of stochastic versus deterministic control see also Menkens [17].

The present paper is motivated by Christiansen and Steffensen [9], where mean-variance-optimal deterministic consumption and investment is discussed in a Black-Scholes market. Sufficient conditions for optimal strategies are derived from a Hamilton-Jacobi-Bellman approach, but only numerical solutions and no analytical solutions are given. That means that the general existence of solutions remains unclear. We fill that gap, allowing for a slightly more general model with non-constant Black-Scholes market parameters. By applying a Pontryagin maximum principle, we additionally verify that the sufficient conditions of Christiansen and Steffensen [9] for optimal controls are actually necessary. Furthermore, we present an alternative numerical algorithm for the calculation of optimal controls. Therefore, we make use of the variational idea behind the Pontryagin maximum principle. In a first step, we define generalized gradients for our objective function, which, in a second step, allows us to construct a gradient ascent method.

Mean-variance investment is a true classic since the seminal work by Markowitz [16]. Since then various authors have improved and extended the results, see for example Korn and Trautmann [12], Korn [13], Zhou and Li [18], Basak and Chabakauri [3], Kryger and Steffensen [15], Kronborg and Steffensen [14], Alp and Korn [1], Björk, Murgoci and Zhou [5] and others.

Deterministic optimal control is fundamental in Herzog et al. [11] and Geering et al. [10]. But apart from other differences, they disregard income and consumption and focus on the pure portfolio problem without cash flows. Bäuerle and Rieder [2] study optimal investment for both, adapted stochastic strategies and deterministic strategies. They discuss various objectives including mean-variance objectives under constraints. In the present paper, we discuss an unconstrained mean-variance-objective and we also control for consumption.

The paper is structured as follows. In Sect. 2, we set up a basic model framework and specify the optimal consumption and investment problem that we discuss here. In Sect. 3, we present an existence result for the optimal control. Section 4 derives necessary conditions for optimal controls by applying a Pontryagin maximum principle. Section 5 defines and calculates generalized gradients for the objective, which helps to set up a numerical optimization algorithm in Sect. 6. In Sect. 7 we illustrate the numerical algorithm.

2 The Mean-Variance-Optimal Deterministic Consumption and Investment Problem

Let $B([0,T])$ denote the space of bounded Borel-measurable functions, equipped with the uniform norm $\Vert \cdot \Vert _{\infty }$. On some finite time interval $[0,T]$, we assume that we have a continuous income with nonnegative rate $a \in B([0,T])$ and a continuous consumption with nonnegative rate $c \in B([0,T])$. Let $C([0,T])$ bet the set of continuous functions on $[0,T]$. The positive initial wealth $x_{0}$ and the stochastic wealth $X(t)$ at $t>0$ is distributed between a bank account with risk-free interest rate $r\in C([0,T])$ and a stock or stock fund with price process

$$\begin{aligned} \mathrm{d}S(t)=S(t)\alpha (t) \mathrm{d}t+S(t)\sigma (t) \mathrm{d}W(t),\quad S(0)=1, \end{aligned}$$

where $\alpha (t) >r(t)\ge 0$, $\sigma (t) >0$ and $\alpha , \sigma \in C([0,T])$. We write $\pi (t)$ for the proportion of the total value invested in stocks and call it the investment strategy. The wealth process $X(t)$ is assumed to be self-financing. Thus, it satisfies

$$\begin{aligned} \mathrm{d}X(t)=X(t)(r(t)+(\alpha (t) -r(t))\pi (t))\mathrm{d}t+(a(t)-c(t))\mathrm{d}t+X(t)\sigma (t) \pi (t)\mathrm{d}W(t) \end{aligned}$$

(1)

with initial value $X(0)=x_{0}$ and has the explicit representation

$$\begin{aligned} X(t)=x_{0}e^{\int _{0}^{t}\mathrm{d}U}+\int \limits _{0}^{t}(a(s)-c(s))e^{\int _{s}^{t}\mathrm{d}U}\mathrm{d}s, \end{aligned}$$

(2)

where

$$\begin{aligned} \mathrm{d}U(t)&=(r(t)+(\alpha (t) -r(t))\pi (t)-\frac{1}{2}\sigma (t) ^{2}\pi (t)^{2})\mathrm{d}t\nonumber \\&\quad +\sigma (t)\pi (t)\mathrm{d}W(t), \quad U(0)=0. \end{aligned}$$

(3)

It is important to note that the process $(X(t))_{t\ge 0}$ depends on the choice of the investment strategy $(\pi (t))_{t \ge 0}$ and the consumption rate $(c(t))_{t \ge 0}$. In order to make that dependence more visible, we will also write $X=X^{(\pi ,c)}$. For some arbitrary but fixed risk aversion parameter $\gamma >0$ of the investor, we define the risk measure

$$\begin{aligned} MV_{\gamma }[\,\cdot \,]:=E[\,\cdot \,]-\gamma Var[\,\cdot \,]. \end{aligned}$$

We aim to maximize the functional

$$\begin{aligned} G(\pi ,c) := MV_{\gamma }\left[ \int \limits _{0}^{T}e^{-\rho s}c(s)\mathrm{d}s+e^{-\rho T}X^{(\pi ,c)}(T)\right] \end{aligned}$$

(4)

with respect to the investment strategy $\pi$ and the consumption rate $c$. The parameter $\rho \ge 0$ describes the preference for consuming today instead of tomorrow.

3 Existence of Optimal Deterministic Control Functions

In Christiansen and Steffensen [9], where a Hamilton-Jacobi-Bellman approach is used, the existence of optimal control functions is related to the existence of solutions for the Hamilton-Jacobi-Bellman partial differential equation. However, only numerical solutions are available, so the general existence of solutions is unclear. Here, we fill that gap by giving an existence result for optimal deterministic control functions. The proof needs rather weak assumptions, but it is not constructive.

Theorem 1

Let $G:D \rightarrow (-\infty ,\infty )$ be defined by (4) for

$$\begin{aligned} D:=\big \{(\pi ,c)\in B([0,T])\times B([0,T]):\underline{c}(t)\le c(t)\le \overline{c}(t),\quad t\in [ 0,T] \big \} \end{aligned}$$

with lower and upper consumption bounds $\underline{c},\overline{c} \in B([0,T])$. Then, the functional $G$ is continuous and has a finite upper bound.

Proof

We first show that $MV_{\gamma }[X(T)] = MV_{\gamma }[X^{(\pi ,c)}(T)]$ has a finite upper bound that does not depend on $(\pi ,c)$. Defining the stochastic process

$$\begin{aligned} Y(t) := X(t) - \gamma X(t)^2 + \gamma E[X(t)]^2, \quad t \in [0,T], \end{aligned}$$

(5)

we have $MV_{\gamma }[X(T)] = E\left[ Y(T) \right]$. So it suffices to show that $E\left[ Y(T) \right]$ has a finite upper bound that does not depend on $(\pi ,c)$. Since the quadratic variation process of $X$ satisfies $\mathrm{d}[X](t)= X(t)^2 \sigma (t)^2 \pi (t) ^2 \mathrm{d}t$, from Ito’s Lemma we get that

$$\begin{aligned}&\quad \mathrm{d}E[X(t)]=E[X(t)]\,\big \{r(t)+(\alpha (t) -r(t))\pi (t)\big \}\mathrm{d}t+(a(t)-c(t))\mathrm{d}t,\end{aligned}$$

(6)

$$\begin{aligned}&\,\begin{array}{ll} \mathrm{d}E[X(t)^2] &{} = 2 E[X(t)^2] \big \{r(t)+(\alpha (t) -r(t))\pi (t)\big \}\mathrm{d}t + E[X(t)]\, (a(t)-c(t)) \mathrm{d}t \\ &{} \quad +\, E[X(t)^2] \sigma (t)^2 \pi (t) ^2 \mathrm{d}t. \end{array} \end{aligned}$$

(7)

Hence, the expectation function of $Y$ solves the differential equation

$$\begin{aligned} \begin{array}{ll} \mathrm{d}E[Y(t)] &{}= E[X(t)]\,\big \{ r(t)+(\alpha (t) -r(t))\pi (t)\big \}\mathrm{d}t+(a(t)-c(t))\mathrm{d}t\\ &{} \quad -\, \gamma E[X(t)^2] \sigma (t)^2 \pi (t) ^2 \mathrm{d}t- 2 \gamma \big (E[X(t)^2]- E[X(t)]^2 \big )\\ &{}\quad \times \,\big \{r(t)+(\alpha (t) -r(t))\pi (t)\big \}\mathrm{d}t . \end{array} \end{aligned}$$

(8)

The right hand side of (8) is maximal with respect to $\pi (t)$ for

$$\begin{aligned} \pi ^{*} (t) = \frac{1}{2\gamma }\frac{\alpha (t)-r(t)}{\sigma (t)^2} \frac{E[X(t)]- 2\gamma \, \mathrm{Var}[ X(t)]}{E[X(t)^2]}. \end{aligned}$$

(9)

Plugging (9) into (8) and rearranging terms yields

$$\begin{aligned} \begin{array}{ll} \mathrm{d}E[Y(t)] &{}\le r(t) \big (E[X(t)] -2\gamma Var[X(t)]\big ) \mathrm{d}t + (a(t)-c(t))\mathrm{d}t \\ &{} \qquad +\,\displaystyle {\frac{1}{4\gamma }}{\frac{(\alpha (t)-r(t))^2}{\sigma (t)^2}} {\frac{\big (E[X(t)]- 2\gamma \, \mathrm{Var}[ X(t)]\big )^2}{E[X(t)^2]}}\mathrm{d}t. \end{array} \end{aligned}$$

(10)

Recall that we assumed $\gamma >0$ and $\sigma (t) >0$, so the first and second denominator are never zero. If the third denominator $E[X(t)^2]$ is zero, we implicitly get $E[X(t)]=0$, and (10) is still true by defining $0/0:=0$. The first line on the right hand side of (10) has an upper bound of

$$\begin{aligned} r(t)\, E[Y(t)] \mathrm{d}t + (a(t)-c(t)) \mathrm{d}t. \end{aligned}$$

With the help of the equality

$$\begin{aligned} \big (E[X(t)]- 2\gamma \, \mathrm{Var}[ X(t)]\big )^2 = E[X(t)]^2 - 4 \gamma \, \mathrm{Var} [X(t)] \, E[Y(t)] \end{aligned}$$

and the inequalities $(E[X(t)])^2 \le E[X(t)^2]$ and $\mathrm{Var}[X(t)]\le E[X(t)^2]$, we can show that the second line on the right hand side of (10) has an upper bound of

$$\begin{aligned} \frac{1}{4\gamma }\frac{(\alpha (t)-r(t))^2}{\sigma (t)^2} \Big ( 1 + 4\gamma \,|E[Y(t)]|\Big ) \mathrm{d}t. \end{aligned}$$

All in all, we obtain

$$\begin{aligned} \mathrm{d}E[Y(t)]&\le \big ( C_1 |E[Y(t)]| + C_2\big ) \mathrm{d}t, \quad t \in [0,T] \end{aligned}$$

(11)

for some finite positive constants $C_1$ and $C_2$, since the functions $r(t), a(t), \alpha (t)$ are uniformly bounded on $[0,T]$, since $- c(t) \le - \underline{c}(t)$ for a uniformly bounded function $\underline{c}$, and since the positive and continuous function $\sigma (t)$ has a uniform lower bound greater than zero. Thus, we have $E[Y(t)] \le g(t)$ for $g(t)$ defined by the differential equation

$$\begin{aligned} \mathrm{d} g(t) = \big ( C_1\, |g(t)| + C_2\big ) \mathrm{d}t, \quad g(0) = Y(0) = x_0 >0. \end{aligned}$$

(12)

This differential equation for $g(t)$ has a unique solution, which is bounded on $[0,T]$ and does not depend on the choice of $(\pi ,c)$. Hence, also $MV_{\gamma }[X(T)] =E[Y(T)]$ has a finite upper bound that does not depend on the choice of $(\pi ,c)$. The same is true for the functional (4), since

$$\begin{aligned} G(\pi ,c) \le \int \limits _{0}^{T}e^{-\rho s}\overline{c}(s)\mathrm{d}s+ e^{-\rho T} MV_{\gamma e^{-\rho T} }\left[ X(T)\right] . \end{aligned}$$

Now we show the continuity of the functional $G$. Suppose that $(\pi _n,c_n)_{n\ge 1}$ is an arbitrary but fixed sequence in $D$ that converges to $(\pi _0,c_0)$ with respect to the supremum norm. Since $D$ is a Banach space, the limit $(\pi _0,c_0)$ is also an element of $D$. Let $X_n(t) := X^{(\pi _n,c_n)}(t)$ for all $t$. As the sequence $(\pi _n,c_n)_{n\ge 1}$ is convergent and within $D$, the absolutes $|\pi _n(t)|$ and $|c_n(t)|$ have finite upper bounds, uniformly in $n$ and uniformly in $t$. Therefore, analogously to inequality (11), from Eq. (6) we get that

$$\begin{aligned} \mathrm{d}E[X_n(t)]&\le \big ( C_3 \,|E[X_n(t)]| + C_4\big ) \mathrm{d}t, \quad t \in [0,T], \quad n=0,1,2,\ldots \end{aligned}$$

for some positive finite constants $C_3$ and $C_4$. Arguing analogously to (12), we obtain that $E[X_n(t)] \le f(t)$ for some bounded function $f(t)$. Using similar arguments for $-E[X_n(t)]$, we get that also the absolute $|E[X_n(t)]|$ is uniformly bounded in $n$ and in $t$. Applying Eq. (7), we obtain

$$\begin{aligned} \mathrm{d}E[X_n(t)^2]&= 2 E[X_n(t)^2] \big \{r(t)+(\alpha (t) -r(t))\pi _n (t)\big \}\mathrm{d}t \\&\quad + E[X_n(t)]\, (a(t)-c_n(t)) \mathrm{d}t+ E[X_n(t)^2] \sigma (t)^2 \pi _n(t) ^2 \mathrm{d}t. \end{aligned}$$

Using the uniform boundedness of $|E[X_n(t)]|$, $|\pi _n(t)|$ and $|c_n(t)|$, we can conclude that

$$\begin{aligned} \mathrm{d}E[X_n(t)^2]&\le \big ( C_5 \,E[X_n(t)^2] + C_6\big ) \mathrm{d}t, \quad t \in [0,T], \quad n=0,1,2,\ldots \end{aligned}$$

for some positive finite constants $C_5$ and $C_6$. Hence, arguing analogously to above, the value $E[X_n(t)^2]$ is uniformly bounded in $n$ and in $t$. Let $Y_n(t)$ be the process according to definition (5) but with $X_n$ instead of $X$. Using (8) and the uniform boundedness of $|E[X_n(t)]|$, $E[X_n(t)^2]$, $|\pi _n(t)|$ and $|c_n(t)|$, we can show that

$$\begin{aligned} \mathrm{d}E[Y_0(t)-Y_n(t)]&\le \bigg ( C_7\, \sup _{t\in [0,T]}| \pi _0(t)- \pi _n(t)| + \sup _{t\in [0,T]}| c_0(t)- c_n(t)|\bigg ) \mathrm{d}t, \quad t \in [0,T] \end{aligned}$$

for some positive finite constant $C_7$. Thus, we get

$$\begin{aligned} E[Y_0(T)-Y_n(T)] \le T\,C_7\, \sup _{t\in [0,T]}| \pi _0(t)- \pi _n(t)| + T \,\sup _{t\in [0,T]}| c_0(t)- c_n(t)|, \end{aligned}$$

where we used that $Y_0(0)-Y_n(0)=x_0-x_0=0$. Arguing similarly for $-E[Y_0(t)-Y_n(t)]$, we can conclude that

$$\begin{aligned}&|G(\pi _0,c_0) - G(\pi _n,c_n)| \\&= \Big | \int \limits _0^Te^{-\rho s} (c_0(s)-c_n(s)) \mathrm{d}s + e^{-\rho T} MV_{\gamma e^{-\rho T} }\left[ X_0(T)\right] - e^{-\rho T} MV_{\gamma e^{-\rho T} }\left[ X_n(T)\right] \Big |\\&\le T \, \sup _{t\in [0,T]}| c_0(t)- c_n(t)| + e^{-\rho T} \big | E[\widetilde{Y}_0(T)-\widetilde{Y}_n(T)] \big |\\&\le T\,C_8\, \sup _{t\in [0,T]}| \pi _0(t)- \pi _n(t)| + 2T \,\sup _{t\in [0,T]}| c_0(t)- c_n(t)| \end{aligned}$$

for some finite constant $C_8$, where the processes $\widetilde{Y}_0(t)$ and $\widetilde{Y}_n(t)$ are defined as above but with $\gamma$ replaced by $\gamma e^{-\rho T}$. Since we assumed that $(\pi _n,c_n)_{n\ge 1}$ converges in supremum norm, we obtain that $G(\pi _n,c_0)$ converges to $G(\pi _0,c_0)$, i.e. the functional $G$ is continuous.

As $G$ has a finite upper bound on the domain $D$, the supremum

$$\begin{aligned} \sup _{(\pi ,c)\in D} G(\pi , c) \end{aligned}$$

indeed exists. Since $G$ is continuous and $D$ is a Banach space, we can conclude that on each compact subset $K$ of $D$ there exists a pair $(\pi ^{*}, c^{*})$ for which

$$\begin{aligned} G(\pi ^{*}, c^{*}) = \sup _{(\pi ,c)\in K} G(\pi , c). \end{aligned}$$

(13)

4 A Pontryagin Maximum Principle

Christiansen and Steffensen [9] identify characterizing equations for optimal investment and consumption rate by using a Hamilton-Jacobi-Bellman approach. Here, we show that those characterizing equations are indeed necessary by using a Pontryagin maximum principle (cf. Bertsekas [4]).

Defining the moment functions

$$\begin{aligned} \begin{array}{ll} m_{i}(t)&{}=E[(X(t))^i],\qquad i=1,2,\\ p_{i}(t)&{} =E[(\int _{t}^{T}\left( a(s)-c(s)\right) e^{\int _{s}^{T}\mathrm{d}U}\mathrm{d}s)^{i}], \qquad i=1,2, \\ n_{i}(t)&{} =E[e^{i\int _{t}^{T}\mathrm{d}U}], \qquad i=1,2, \\ k(t)&{} =E[e^{\int _{t}^{T}\mathrm{d}U}\int _{t}^{T}(a(s)-c(s))e^{\int _{s}^{T}\mathrm{d}U}\mathrm{d}s], \end{array} \end{aligned}$$

(14)

as in Christiansen and Steffensen [9], we can represent the objective function $G(\pi ,c)$ by

$$\begin{aligned} \begin{array}{ll} G(\pi ,c) &{} =\int \limits _{0}^{T}e^{-\rho s} c(s)\mathrm{d}s+e^{-\rho T}\left( m_{1}( t) n_{1}( t) +p_{1}( t) \right) \\ &{} \quad -\gamma e^{-2\rho T} \left( m_{2}(t) n_{2}( t) +2m_{1}( t) k( t) +p_{2}( t) -\left( m_{1}( t) n_{1}( t) +p_{1}( t) \right) ^{2}\right) \end{array}\end{aligned}$$

(15)

for any $t$ in $[0,T]$. Simple calculations give us that

$$\begin{aligned} \begin{array}{ll} \frac{{\mathrm{d}}}{{\mathrm{d}t}}m_{1}(t) &{}=\left( r(t)+(\alpha (t) -r(t))\pi (t)\right) m_{1}(t)+(a(t)-c(t)), \\ \frac{{\mathrm{d}}}{{\mathrm{d}t}}m_{2}( t) &{}=\left( 2r(t)+2\left( \alpha (t) -r(t)\right) \pi ( t) +\pi ( t)^{2}\sigma (t) ^{2}\right) m_{2}( t) +2\left( a( t) -c\left( t\right) \right) m_{1}( t). \end{array}\end{aligned}$$

(16)

Similarly to $m_{1}$ and $m_{2}$, also $n_{1}$, $n_{2}$, $p_{1}$, $p_{2}$, and $k$ solve a system of ordinary differential equations but with terminal instead of initial conditions, see Christiansen and Steffensen [9].

Theorem 2

Let $(\pi ^{*}, c^{*})$ be an optimal control in the sense of (13), and let $m^{*}_i(t)$, $p^{*}_i(t)$, $n^{*}_i(t)$, $i=1,2$, and $k^{*}(t)$ be the corresponding moment functions according to (14). Then, we have necessarily

$$\begin{aligned} \pi ^{*}(t)&=\frac{\alpha (t) -r(t)}{\sigma (t) ^{2}}\bigg (\frac{ e^{\rho T}m_{1}^{*}(t)n_{1}^{*}(t) -2\gamma m_{1}^{*}(t)\Big (k^{*}(t)-n_{1}^{*}(t)m^{*}_1(T) \Big )}{2\gamma m_{2}^{*}(t)n_{2}^{*}(t)} -1\bigg ), \end{aligned}$$

(17)

$$\begin{aligned} c^{*}(t)&=\left\{ {\begin{array}{ll} \overline{c}(t) &{}\quad \mathrm{if }\; e^{\rho (T-t)}-n_{1}^{*}(t)+2\gamma e^{-\rho T}\Big (m_{1}^{*}(t)n_{2}^{*}(t)+ k^{*}(t)-n_{1}^{*}(t)m_{1}^{*}(T)\Big ) > 0\\ \underline{c}(t)&{} \quad \mathrm{else. } \end{array}} \right. \end{aligned}$$

(18)

Proof

With $(\pi ^{*},c^{*})$ being an optimal control, we define local alternatives by

$$\begin{aligned} (\pi ^{\varepsilon }(t),c^{\varepsilon }(t)) = \left\{ \begin{array}{ll} (\pi ^{*}(t),c^{*}(t))+ (h(t),l(t)) &{}\quad \mathrm{for }\; t \in (t_0-\varepsilon , t_0] \\ (\pi ^{*}(t),c^{*}(t)) &{}\quad \mathrm{else} \\ \end{array} \right. \end{aligned}$$

for continuous functions $h$ and $l$. As $G(\pi ^{*},c^{*})$ is maximal, by applying (15) for $t=t_0$ we obtain that

$$\begin{aligned} G(\pi ^{*},c^{*}) - G(\pi ^{\varepsilon },c^{\varepsilon })&= - \int \limits _{t_0-\varepsilon }^{t_0}e^{-\rho s} l(s)\mathrm{d}s+e^{-\rho T}\big ( m^{*}_{1}( t_0) - m^{\varepsilon }_1(t_0) \big ) n^{*}_1( t_0) \nonumber \\&\quad -\,\gamma e^{-2\rho T} \Big \{ \big (m^{*}_{2}( t_0) - m^{\varepsilon }_2(t_0) \big ) n^{*}_{2}( t_0) +2\big (m^{*}_{1}( t_0) - m^{\varepsilon }_1(t_0) \big ) k^{*}( t_0) \nonumber \\&\qquad \qquad \qquad \qquad -\,\big ( m^{*}_{1}( t_0)^2-m^{\varepsilon }_1( t_0)^2 \big ) n^{*}_{1}( t_0)^2 - 2( m^{*}_{1}( t_0)\nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad -\, m_1^{\varepsilon }( t_0) ) n^{*}_1(t_0) p^{*}_{1}( t_0) \Big \}\nonumber \\&= - \int \limits _{t_0-\varepsilon }^{t_0}e^{-\rho s} l(s)\mathrm{d}s + \big ( m^{*}_{1}( t_0) - m^{\varepsilon }_1(t_0) \big )\nonumber \\&\quad \times \, \Big \{ e^{-\rho T} n^{*}_1( t_0) - 2\gamma e^{-2\rho T} \big ( k^{*}( t_0) - n^{*}_1(t_0) p^{*}_{1}( t_0)\big ) \Big \}\nonumber \\&\quad -\, \big ( m^{*}_{1}( t_0)^2-m^{\varepsilon }_1( t_0)^2 \big ) \gamma e^{-2\rho T} n^{*}_{1}( t_0)^2\nonumber \\&\quad -\, \big (m^{*}_{2}( t_0) - m^{\varepsilon }_2(t_0) \big ) \gamma e^{-2\rho T} n^{*}_{2}( t_0) \end{aligned}$$

(19)

must be nonnegative. Equation (16) implies that

$$\begin{aligned} m^{*}_{1}( t_0) - m^{\varepsilon }_1(t_0)&= \int \limits _{t_0-\varepsilon }^{t_0} \Big (\frac{{\mathrm{d}}}{{\mathrm{d}s}} m^{*}_{1}( s) - \frac{\mathrm{d}}{{\mathrm{d}s}} m^{\varepsilon }_1(s)\Big )\mathrm{d}s\\&= \int \limits _{t_0-\varepsilon }^{t_0}\bigg ( \Big \{ \big (r(s) + (\alpha (s) -r(s) )\pi ^{*}(s)\big ) m_1^{*}(s) \\&\qquad \qquad \qquad - \big (r(s) + (\alpha (s) -r(s) )\pi ^{\varepsilon }(s)\big ) m_1^{\varepsilon }(s) \Big \} + l(s) \bigg ) \mathrm{d}s, \end{aligned}$$

since $\Vert m^{*}_1- m^{\varepsilon }_1\Vert \rightarrow 0$ for $\varepsilon \rightarrow 0$. Moreover, since we have $m^{*}_1(t) \rightarrow m^{*}_1(t_0)$, $r(t) \rightarrow r(t_0)$, $\alpha (t) \rightarrow \alpha (t_0)$, $\sigma (t) \rightarrow \sigma (t_0)$ for $t\rightarrow t_0$, we get that

$$\begin{aligned} m^{*}_{1}( t_0) - m^{\varepsilon }_1(t_0)&= - (\alpha (t_0) -r(t_0) ) \, m_1^{*}(t_0) \int \limits _{t_0-\varepsilon }^{t_0}h(s) \mathrm{d}s + \int \limits _{t_0-\varepsilon }^{t_0}l(s) \mathrm{d}s + o(\varepsilon ). \end{aligned}$$

(20)

For the squared functions we use

$$\begin{aligned} m^{*}_{1}( t_0)^2 - m^{\varepsilon }_1(t_0)^2&= \big (m^{*}_{1}( t_0) - m^{\varepsilon }_1(t_0)\big )\big (m^{*}_{1}( t_0) + m^{\varepsilon }_1(t_0)\big )\\&= 2 m^{*}_{1}( t_0) \big (m^{*}_{1}( t_0) - m^{\varepsilon }_1(t_0)\big ) - \big (m^{*}_{1}( t_0) - m^{\varepsilon }_1(t_0)\big )^2 \end{aligned}$$

and then apply the asymptotic formula (20), which leads to

$$\begin{aligned} m^{*}_{1}( t_0)^2 - m^{\varepsilon }_1(t_0)^2&= - 2 (\alpha (t_0) -r(t_0) ) \, m_1^{*}(t_0)^2 \int \limits _{t_0-\varepsilon }^{t_0}h(s) \mathrm{d}s\\&\quad + 2 m_1^{*}(t_0) \int \limits _{t_0-\varepsilon }^{t_0}l(s) \mathrm{d}s + o(\varepsilon ). \end{aligned}$$

Similarly, we can show that

$$\begin{aligned}&\begin{array}{ll} m^{*}_{2}( t_0) - m^{\varepsilon }_2(t_0) &{} = \Big \{-2(\alpha (t_0) -r(t_0) )\, m_2^{*}(t_0) \\ &{}\quad -\, 2\pi ^{*}(t_0) \sigma (t_0)^2 m_2^{*}(t_0) \Big \} \int \limits _{t_0-\varepsilon }^{t_0}h(s) \mathrm{d}s \\ &{}\quad +\, 2 m_1^{*}(t_0) \int \limits _{t_0-\varepsilon }^{t_0}l(s) \mathrm{d}s + o(\varepsilon ). \end{array} \nonumber \\[-16pt] \end{aligned}$$

(21)

Plugging Eq. (21) into Eq. (19) and rearranging, we get

$$\begin{aligned} o ( \varepsilon )&\le \int \limits _{t_0-\varepsilon }^{t_0} l(s) \mathrm{d}s \bigg (-e^{\rho t_0} + e^{-\rho T} n_1^{*}(t_0) - 2 \gamma e^{-2\rho T} \Big \{ m_1^{*}(t_0)n_2^{*}(t_0)+ k^{*}(t_0) \\&\qquad \qquad \qquad \qquad -n_1^{*}(t_0) \big ( n_1^{*}(t_0) m_1^{*}(t_0)+p_1^{*}(t_0)\big )\Big \} \bigg )\\&\quad + \int \limits _{t_0-\varepsilon }^{t_0} h(s)\; \mathrm{d}s \, (\alpha (t_0)-r(t_0)) \bigg ( - m_1^{*}(t_0)n_1^{*}(t_0) e^{-\rho T}- 2\gamma e^{-2\rho T} m_1^{*}(t_0)\\&\quad \qquad \qquad \qquad \qquad \times \Big \{- k^{*}(t_0) + n_1^{*}(t_0) \big (n_1^{*}(t_0) m_1^{*}(t_0)+p_1^{*}(t_0) \big ) \Big \} \bigg )\\&\quad - 2\gamma e^{-2\rho T} m_2^{*}(t_0)n_2^{*}(t_0) \Big \{ -1 - \pi ^{*}(t_0) \frac{\sigma (t_0)^2}{\alpha (t_0)-r(t_0)} \Big \} \end{aligned}$$

for all continuous functions $l$ and $h$. Note that $n_1^{*}(t_0) m_1^{*}(t_0)+p_1^{*}(t_0) = m_1^{*}(T)$. Consequently, we must have that the sign of $l(t_0)$ equals the sign of

$$\begin{aligned} -e^{\rho t_0} + e^{-\rho T} n_1^{*}(t_0) - 2 \gamma e^{-2\rho T} \Big ( m_1^{*}(t_0)n_2^{*}(t_0)+ k^{*}(t_0) -n_1^{*}(t_0) m_1^{*}(T)\Big ), \end{aligned}$$

which means that (18) holds, and we have necessarily that

$$\begin{aligned} \begin{array}{ll} 0=&{} - m_1^{*}(t_0)n_1^{*}(t_0) e^{-\rho T}- 2\gamma e^{-2\rho T} m_2^{*}(t_0)n_2^{*}(t_0) \Big ( -1 - \pi ^{*}(t_0) \frac{\sigma (t_0)^2}{\alpha (t_0)-r(t_0)} \Big ) \\ &{} - 2\gamma e^{-2\rho T} m_1^{*}(t_0) \Big (- k^{*}(t_0) + n_1^{*}(t_0) m_1^{*}(T) \Big ), \end{array}\end{aligned}$$

(22)

which means that (17) is satisfied.

Recalling that $n_1^{*}(t_0) m_1^{*}(t_0)+p_1^{*}(t_0) = m_1^{*}(T)$, we observe that Eqs. (17) and (18) are equal to Eqs. (19) and (20) in Christiansen and Steffensen [9], which means that the latter equations are not only sufficient but also necessary.

5 Generalized Gradients for the Objective

For differentiable functions on the Euclidean space, a popular method to find maxima is to use the gradient ascent method. We want to follow that variational concept, however our objective is a mapping on a functional space. Therefore, we first need to discuss the definition and calculation of proper gradient functions.

Theorem 3

Let $(\pi ,c) \in D$ for $D$ as defined in Theorem 1. For each pair of continuous functions $(h,l)$ on $[0,T]$, we have

$$\begin{aligned} \lim _{\delta \rightarrow 0} \frac{G(\pi +\delta h, c +\delta l) -G(\pi ,c)}{\delta }&= \int \limits _0^T h(s) (\nabla _{\pi } G(\pi ,c))(s) \mathrm{d}s\\&\quad + \int \limits _0^T l(s) (\nabla _{c} G(\pi ,c))(s) \mathrm{d}s \end{aligned}$$

with

$$\begin{aligned} (\nabla _{\pi } G(\pi ,c))(s)&= (\alpha (s)-r(s))\bigg ( m_1(s)n_1(s) e^{-\rho T}- 2\gamma e^{-2\rho T} m_2(s)n_2(s) \\&\quad \quad \qquad \qquad \qquad \qquad \times \Big ( 1 + \pi (s) \frac{\sigma (s)^2}{\alpha (s)-r(s)} \Big ) - 2\gamma e^{-2\rho T} m_1(s) \\&\qquad \qquad \qquad \qquad \qquad \times \Big ( k(s) - n_1(s) m_1(T)\Big )\bigg ) \end{aligned}$$

and

$$\begin{aligned} (\nabla _{c} G(\pi ,c))(s)&= e^{\rho s} - e^{-\rho T} n_1(s) \\&\quad + 2 \gamma e^{-2\rho T} \Big ( m_1(s)n_2(s)+ k(s) -n_1(s) m_1(T)\Big ) . \end{aligned}$$

The limit

$$\begin{aligned} \lim _{\delta \rightarrow 0} \frac{G(\pi +\delta h, c +\delta l) -G(\pi ,c)}{\delta } = \frac{\mathrm{d}}{\mathrm{d}\delta }\Big |_{\delta =0} G(\pi +\delta h, c +\delta l) \end{aligned}$$

is the so-called Gateaux derivative (or directional derivative) of the functional $G$ at $(\pi ,c)$ in direction $(h,l)$. Following Christiansen [7], we interpret the two-dimensional function $(\nabla _{\pi } G(\pi ,c), \nabla _{\pi } G(\pi ,c))$ as the gradient of $G$ at $(\pi ,c)$.

Proof

(Proof of Theorem 3) In the proof of Theorem 2 we already implicitly showed that

$$\begin{aligned} G(\pi , c ) -G(\pi +h \mathbf 1 _{(t_0-\varepsilon ,t_0]},c+l\mathbf 1 _{(t_0-\varepsilon ,t_0]})&= -(\nabla _{\pi } G(\pi ,c))(t_0) \int \limits _{t_0-\varepsilon }^{t_0} h(s) \mathrm{d}s \\&\quad -(\nabla _{c} G(\pi ,c))(t_0) \int \limits _{t_0-\varepsilon }^{t_0} l(s) \mathrm{d}s +o ( \varepsilon ) \end{aligned}$$

for all $t_0 \in [0,T]$, $(\pi ,c) \in D$, and $h,l \in C([0,T])$. Defining an equidistant decomposition of the interval $[0,T]$ by

$$\begin{aligned} \tau _i := \frac{i}{n} T, \quad i=0,\ldots ,n, \end{aligned}$$

we can rewrite the difference $G(\pi +\delta h,c+\delta l) - G(\pi , c )$ to

$$\begin{aligned}&G(\pi +\delta h,c+\delta l) - G(\pi , c )\\&= \sum _{i=1}^n \Big ( G(\pi + \delta h \mathbf 1 _{[0,\tau _i]},c+\delta l\mathbf 1 _{[0,\tau _i]})-G(\pi +\delta h \mathbf 1 _{[0,\tau _{i-1}]},c+\delta l\mathbf 1 _{[0, \tau _{i-1}]}) \Big )\\&= \delta \sum _{i=1}^n(\nabla _{\pi } G(\pi +\delta h \mathbf 1 _{[0,\tau _{i-1}]},c+\delta l\mathbf 1 _{[0,\tau _{i-1}]}))(\tau _{i}) \int \limits _{\tau _{i-1}}^{\tau _i} h(s) \mathrm{d}s \\&\quad + \delta \sum _{i=1}^n (\nabla _{c} G(\pi +\delta h \mathbf 1 _{[0,\tau _{i-1}]},c+\delta l\mathbf 1 _{[0,\tau _{i-1}]}))(\tau _i) \int \limits _{\tau _{i-1}}^{\tau _i}l(s) \mathrm{d}s +\sum _{i=1}^n o ( T/n) \end{aligned}$$

for all $0 < \delta \le 1$. The moments $p_1,p_2,n_1,n_2,k$, interpreted as mappings of $(\pi ,c)$ from the domain $B([0,T])^2$ with $L_2$-norm into the codomain $C([0,T])$ with supremum norm, are continuous. Hence, the gradient functions on the right hand side of the last equation are continuous with respect to the parameters $\tau _{i-1}$ and $\tau _{i}$. Thus, for $n\rightarrow \infty$ we obtain

$$\begin{aligned} \frac{G(\pi +\delta h,c+\delta l) - G(\pi , c )}{\delta }&= \int \limits _0^T (\nabla _{\pi } G(\pi +\delta h \mathbf 1 _{[0,t]},c+\delta l\mathbf 1 _{[0,s]}))(s) h(s) \mathrm{d}s \\&\quad + \int \limits _0^T (\nabla _{c} G(\pi +\delta h \mathbf 1 _{[0,s]},c+\delta l\mathbf 1 _{[0,s]}))(s) l(s) \mathrm{d}s. \end{aligned}$$

Since the moment functions $p_1,p_2,n_1,n_2,k$ (interpreted as mappings of $(\pi ,c)$ from the domain $B([0,T])^2$ with supremum-norm into the codomain $C([0,T])$ with supremum norm) are even uniformly continuous, the above gradient functions are uniformly continuous with respect to parameter $\delta$. Thus, for $\delta \rightarrow 0$ we end up with the statement of the theorem.

6 Numerical Optimization by a Gradient Ascent Method

With the help of the gradient function $(\nabla _{\pi } G(\pi ,c), \nabla _{\pi } G(\pi ,c))$ of the objective $G(\pi ,c)$, we can construct a gradient ascent method. A similar approach is also used in Christiansen [8].

Algorithm

• 1. Choose a starting control $(\pi ^{(0)},c^{(0)})$.

• 2. Calculate a new scenario by using the iteration

  $$\begin{aligned} (\pi ^{(i+1)},c^{(i+1)}) := (\pi ^{(i)},c^{(i)}) + K\, \Big (\nabla _{\pi } G(\pi ^{(i)},c^{(i)}), \nabla _{\pi } G(\pi ^{(i)},c^{(i)})\Big ) \end{aligned}$$

  where $K > 0$ is some step size that has to be chosen. If $c^{(i+1)}$ is above or below the bounds $\overline{c}$ and $\underline{c}$, we cut it off at the bounds.

• 3. Repeat step 2 until $\big | G(\pi ^{(i+1)},c^{(i+1)}) - G(\pi ^{(i)},c^{(i)})\big |$ is below some error tolerance.

7 Numerical Example

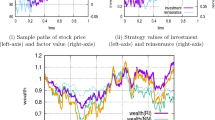
Here, we demonstrate the gradient ascent method of the previous section with a numerical example. For simplicity, we fix the consumption rate $c$ and only control the investment rate $\pi$. We take the same parameters as in Christiansen and Steffensen [9] in order to have comparable results: For the Black-Scholes market we assume that $r=0.04$, $\alpha =0.06$ and $\sigma =0.2$. The time horizon is set to $T=20$, the initial wealth is $x_{0}=200$, and the savings rate is $a(t)-c(t)=100-80=20$. The preference parameter of consuming today instead tomorrow is set to $\rho =0.1$, and the risk aversion parameter is set to $\gamma =0.003$.

Starting from $\pi ^{(0)}=0.5$, Fig. 1 shows the converging series of investment rates $\pi ^{(i)}$, $i=0,\ldots ,40$ for $K=0.2$. The last iteration step $\pi ^{(40)}$ perfectly fits the corresponding numerical result in Christiansen and Steffensen [9].

Fig. 1

Sequence of investment rates $\pi ^{(i)}$, $i=0,\ldots ,40$ calculated by the gradient ascent method. The higher the number $i$ the darker the color of the corresponding graph