Abstract
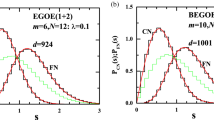
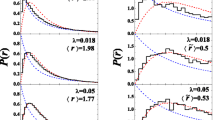
First non-trivial but at the same time very important, from the point of view of its applications, embedded ensemble is the embedded Gaussian orthogonal ensemble of one plus two-body interactions with spin degree of freedom [EGOE(1+2)-s] for a system of interacting fermions. This ensemble is directly applicable, as spin degree of freedom is explicitly included, to mesoscopic systems such as quantum dots and small metallic grains. Extensive numerical calculations are used to show that EGOE(1+2)-s ensemble exhibits three chaos markers, just as the EGOE(1+2) for spinless fermion systems, with the markers depending on the total m fermion spin S. This dependence is derived using propagation equations for fixed-S spectral variances. Spin degree of freedom allows for inclusion of both exchange interaction and pairing interaction in the Hamiltonian and algebraic properties of these two interactions are discussed.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
V.K.B. Kota, R.U. Haq, Spectral Distributions in Nuclei and Statistical Spectroscopy (World Scientific, Singapore, 2010)
J.M. Deutsch, Quantum statistical mechanics in a closed system. Phys. Rev. A 43, 2046–2049 (1991)
M. Srednicki, Chaos and quantum thermalization. Phys. Rev. E 50, 888–901 (1994)
M. Rigol, V. Dunjko, M. Olshanii, Thermalization and its mechanism for generic isolated quantum systems. Nature (London) 452, 854–858 (2008)
L.F. Santos, M. Rigol, Onset of quantum chaos in one dimensional bosonic and fermionic systems and its relation to thermalization. Phys. Rev. E 81, 036206 (2010)
L.F. Santos, M. Rigol, Localization and the effects of symmetries in the thermalization properties of one-dimensional quantum systems. Phys. Rev. E 82, 031130 (2010)
V.K.B. Kota, A. Relaño, J. Retamosa, M. Vyas, Thermalization in the two-body random ensemble, J. Stat. Mech. P10028 (2011)
C. Mejía-Monasterio, G. Benenti, G.G. Carlo, G. Casati, Entanglement across a transition to quantum chaos. Phys. Rev. A 71, 062324 (2005)
S. Montangero, L. Viola, Multipartite entanglement generation and fidelity decay in disordered qubit systems. Phys. Rev. A 73, 040302(R) (2006)
I. Piz̆orn, T. Prosen, T.H. Seligman, Loschmidt echoes in two-body random matrix ensembles. Phys. Rev. B 76, 035122 (2007)
W.G. Brown, L.F. Santos, D.J. Starling, L. Viola, Quantum chaos, delocalization and entanglement in disordered Heisenberg models. Phys. Rev. E 77, 021106 (2008)
V.K.B. Kota, N.D. Chavda, R. Sahu, One plus two-body random matrix ensemble with spin: analysis using spectral variances. Phys. Lett. A 359, 381–389 (2006)
H.E. Türeci, Y. Alhassid, Spin-orbit interaction in quantum dots in the presence of exchange correlations: an approach based on a good-spin basis of the universal Hamiltonian. Phys. Rev. B 74, 165333 (2006)
M. Vyas, V.K.B. Kota, N.D. Chavda, Transitions in eigenvalue and wavefunction structure in (1+2)-body random matrix ensembles with spin. Phys. Rev. E 81, 036212 (2010)
Ph. Jacquod, A.D. Stone, Ground state magnetization for interacting fermions in a disordered potential: kinetic energy, exchange interaction, and off-diagonal fluctuations. Phys. Rev. B 64, 214416 (2001)
L. Kaplan, T. Papenbrock, C.W. Johnson, Spin structure of many-body systems with two-body random interactions. Phys. Rev. C 63, 014307 (2000)
J. Planelles, F. Rajadell, J. Karwowski, Spectral density distribution moments of N-electron Hamiltonians in the low-density limit. J. Phys. A 30, 2181–2196 (1997)
J. Karwowski, Statistical theory of spectra. Int. J. Quant. Chem. 51, 425–437 (1994)
J. Karwowski, F. Rajadell, J. Planelles, V. Mas, The first four moments of spectral density distribution of an N-electron Hamiltonian matrix defined in an antisymmetric and spin-adapted model space. At. Data Nucl. Data Tables 61, 177–232 (1995)
J. Planelles, F. Rajadell, J. Karwowski, V. Mas, A diagrammatic approach to statistical spectroscopy of many-fermion Hamiltonians. Phys. Rep. 267, 161–194 (1996)
K.K. Mon, J.B. French, Statistical properties of many-particle spectra. Ann. Phys. (N.Y.) 95, 90–111 (1975)
J.C. Parikh, Group Symmetries in Nuclear Structure (Plenum, New York, 1978)
V.K.B. Kota, Sizes of effective single particle fields for s-d shell effective interactions. Phys. Rev. C 20, 347–356 (1979)
V.K.B. Kota, K. Kar, Group symmetries in two-body random matrix ensembles generating order out of complexity. Phys. Rev. E 65, 026130 (2002)
K.T. Hecht, Summation relation for U(N) Racah coefficients. J. Math. Phys. 15, 2148–2156 (1974)
K.T. Hecht, J.P. Draayer, Spectral distributions and the breaking of isospin and supermultiplet symmetries in nuclei. Nucl. Phys. A 223, 285–319 (1974)
B. Georgeot, D.L. Shepelyansky, Breit-Wigner width and inverse participation ratio in finite interacting Fermi systems. Phys. Rev. Lett. 79, 4365–4368 (1997)
I. Talmi, Simple Models of Complex Nuclei: The Shell Model and Interacting Boson Model (Harwood Academic Publishers, Chur, 1993)
K.T. Hecht, Some simple R 5 Wigner coefficients and their application. Nucl. Phys. 63, 177–213 (1965)
K.T. Hecht, Five-dimensional quasi-spin the n, T dependence of shell-model matrix elements in the seniority scheme. Nucl. Phys. A 102, 11–80 (1967)
K.T. Hecht, J.P. Elliott, Coherent-state theory for the proton-neutron quasispin group. Nucl. Phys. A 438, 29–40 (1985)
K.T. Hecht, Wigner coefficients for the proton-neutron quasispin group: an application of vector coherent state techniques. Nucl. Phys. A 493, 29–60 (1989)
V.K.B. Kota, J.A. Castilho Alcarás, Classification of states in SO(8) proton-neutron pairing model. Nucl. Phys. A 764, 181–204 (2006)
D.J. Rowe, J.L. Wood, Fundamentals of Nuclear Models: Foundational Models (World Scientific, Singapore, 2010)
M.A. Caprio, J.H. Skrabacz, F. Iachello, Dual algebraic structures for the two-level pairing model. J. Phys. A, Math. Theor. 44, 075303 (2011)
V.K.B. Kota, Two-body ensembles with group symmetries for chaos and regular structures. Int. J. Mod. Phys. E 15, 1869–1883 (2006)
B.G. Wybourne, Symmetry Principles and Atomic Spectroscopy (Wiley, New York, 1970)
M. Vyas, V.K.B. Kota, N.D. Chavda, One-plus two-body random matrix ensembles with spin: results for pairing correlations. Phys. Lett. A 373, 1434–1443 (2009)
C. Quesne, S. Spitz, Spectral distributions of mixed configurations of identical nucleons in the seniority scheme I. Generalized seniority scheme. Ann. Phys. (N.Y.) 85, 115–151 (1974)
C. Quesne, S. Spitz, Spectral distributions of mixed configurations of identical nucleons in the seniority scheme II. Configuration-seniority scheme. Ann. Phys. (N.Y.) 112, 304–327 (1978)
B.J. Dalton, S.M. Grimes, J.P. Vary, S.A. Williams (eds.), Moment Methods in Many Fermion Systems (Plenum, New York, 1980)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2014 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Kota, V.K.B. (2014). One Plus Two-Body Random Matrix Ensembles for Fermions with Spin Degree of Freedom: EGOE(1+2)-s . In: Embedded Random Matrix Ensembles in Quantum Physics. Lecture Notes in Physics, vol 884. Springer, Cham. https://doi.org/10.1007/978-3-319-04567-2_6
Download citation
DOI: https://doi.org/10.1007/978-3-319-04567-2_6
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-04566-5
Online ISBN: 978-3-319-04567-2
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)