Abstract
Data Envelopment Analysis (DEA) employs mathematical programming to measure the relative efficiency of Decision Making Units (DMUs). One of the topics of this chapter is concerned with development of indicators to determine whether or not the specification of the input and output space is supported by data in the sense that the variation in data is sufficient for estimation of a frontier of the same dimension as the input output space. Insufficient variation in data implies that some inputs/outputs can be substituted along the efficient frontier but only in fixed proportions. Data thus locally support variation in a subspace of a lower dimension rather than in the input output space of full dimension. The proposed indicators are related to the existence of so-called Full Dimensional Efficient Facets (FDEFs). To characterize the facet structure of the CCR- or the BCC-estimators, (Charnes et al. Eur J Oper Res 2:429–444, 1978; Banker et al. Manage Sci 30(9):1078–1092, 1984) of the efficient frontier we derive a dual representation of the technologies. This dual representation is derived from polar cones. Relying on the characterization of efficient faces and facets in Steuer (Multiple criteria optimization. Theory, computation and application, 1986), we use the dual representation to define the FDEFs. We provide small examples where no FDEFs exist, both for the CCR- and the BCC estimator. Thrall (Ann Oper Res 66:109–138, 1996) introduces a distinction between interior and exterior facets. In this chapter we discuss the relationship between this classification of facets and the distinction in Olesen and Petersen (Manage Sci 42:205–219, 1996) between non-full dimensional and full dimensional efficient facets. Procedures for identification of all interior and exterior facets are discussed and a specific small example using Qhull to generate all facets is presented. In Appendix B we present the details of the input to and the output from Qhull. It is shown that the existence of well-defined marginal rates of substitution along the estimated strongly efficient frontier segments requires the existence of FDEFs. A test for the existence of FDEFs is developed, and a technology called EXFA that relies only on FDEFs and the extension of these facets is proposed, both in the context of the CCR-model and the BCC-model. This technology is related to the Cone-Ratio DEA. The EXFA technology is used to define the EXFA efficiency index providing a lower bound on the efficiency rating of the DMU under evaluation. An upper bound on the efficiency rating is provided by a technology defined as the (non-convex) union of the input output sets generated from FDEFs only. Finally, we review recent uses of efficient faces and facets in the literature.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
- 2.
In the case of parametric estimation, extreme collinearity is defined as the existence of an exact linear relation among the explanatory variables. However, the distinction between independent and explanatory variables is not straightforward in the context of DEA. Hence, we will refrain from giving any precise definition of extreme collinearity in relation to DEA; it suffices to note that extreme collinearity in relation to DEA includes the case, where there exists a vector a \(\alpha \in \mathbb{R}^{m},\alpha \neq 0\), such that \(\alpha^{T}X=0\), or \(\beta \in \mathbb{R}^{s},\beta \neq 0\), such that \(\beta^{T}Y=0\), where X is the \(m\times N\) matrix of N input vectors and Y is the \(s\times N\) matrix of N output vectors from N DMUs.
- 3.
n corresponds to the number of inputs and outputs in a DEA analysis.
- 4.
In this paper we take the term facet of a convex polyhedral set \(P\in \mathbb{R}^{n}\) to mean a maximal face of P distinct from P (maximal under inclusion), (see Klee 1953; Schrijver 1986). Furthermore, we follow this definition in our specification of the term efficient facet in the sense that an efficient facet is a maximal efficient face, i.e. an efficient face not included in any other efficient face. Using this definition of the term efficient facet we may encounter efficient facets of any dimension \(d,1\leq d\leq n-1\); efficient facets of dimension n-1 is termed full dimensional efficient facets (FDEF). However, as pointed out by one of the referees of (Olesen and Petersen 1996), some authors define a facet of a convex polyhedral set in \(\mathbb{R}^{n}\) as a face of dimension n − 1; consequently, all facets are of dimension n − 1 and a non full dimensional facet does not exist. Following that tradition a FDEF is simply an efficient facet and a non-FDEF is a maximal efficient face of dimension less than n − 1.
- 5.
Thrall (1996) distinguishes between interior and exterior facets. In this notation ABC is an interior facet and ACc’a’ is an exterior facet. We will return to this classification of facets in Sect. Sect. 6.4.
- 6.
An efficient point \(\left( x_{o},y_{o}\right)\) in the production possibility set T is weakly efficient if \(\left( \theta x_{o},y_{o}\right) \notin T,\forall \theta \in \left( 0,1\right)\) and \(\left( \left\{ \left( x,y\right) :x\leq x_{o},y\geq y_{o}\right\} \cap T\right) \backslash \left\{ \left( x_{o},y_{o}\right) \right\} \neq \varnothing\). \(\left( x_{o},y_{o}\right)\) is strongly efficient if \(\left\{ \left( x,y\right) :x\leq x_{o},y\geq y_{o}\right\} \cap T=\left\{ \left( x_{o},y_{o}\right) \right\}\). Charnes et al. (1991, p. 205) further classify a strongly efficient DMUj in relation to the CCR-model as being extreme efficient if the dimension of the cone of feasible multipliers
$$ \mathcal{F}^{CCR}\left( \left\{ j\right\} \right) \equiv \left\{\left( u,-v\right) \in \mathcal{P}_{CCR},u^{T}Y_{j}-v^{T}X_{j}=0\right\}$$in (6.5) below is equal to \(s+m\). Otherwise, the strongly efficient DMU is denoted non-extreme efficient.
- 7.
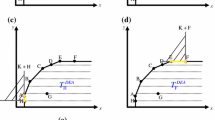
It is a peculiar phenomenon that any CCR frontier with at least two extreme efficient observations in a three dimensional input output space will have no non full dimensional efficient facets. To illustrate geometrically the concept of a non full dimensional efficient facet we need at least a four dimensional input output space. Hence, for a geometric illustration of this concept (Olesen and Petersen 1996) use an output isoquant in a three dimensional output space. Notice however, that it is very easy to illustrate a non full dimensional efficient facet in the BCC model in a three dimensional input output space, see below.
- 8.
The problem is thus of the same nature as collinearity in the parametric approach.
- 9.
See note 6.
- 10.
\( conv\left( \left\{ z_{1},\ldots,z_{n}\right\} \right) \equiv \left\{ z | z=\sum\limits_{j=1}^{n}\lambda _{j}z_{j},\sum\limits_{j=1}^{n}\lambda_{j}=1,\lambda_{j}\in \left[ 0,1 \right],\forall j\right\}.\)
- 11.
\(\left\vert \mathbb{E} \right\vert\) denotes the number of elements in the index set \(\mathbb{E}\).
- 12.
\(\left\vert J\right\vert\) denotes the number of elements in the index set J.
- 13.
In other words we know the convex set in either sum form or in intersection form.
- 14.
- 15.
- 16.
Actually, it is recommended only to put one number on each line in the input file to Qhull.
- 17.
How to specify M relatively to the size of the numbers expressing the inputs and outputs is left for further research. Clearly, there is a trade-off between precision and numerical stability of the results obtained from Qhull. If high precision of the normal vectors and the offsets is of importance then one probably should “reestimate” these vectors as soon as the vertices on each facet are identified. Consider e.g. a facet containing the vertices \(\left(0,0,0,0\right),\left( x_{11},x_{21},y_{11},y_{21}\right),\left(M,0,0,0\right),\left( 0,0,-M,0\right).\) A second stage reestimation of the normal vector would be an estimation of the hyperplane containing the following four points: \(\left( 0,0,0,0\right),\left( x_{11},x_{21},y_{11},y_{21}\right),\left(x_{11}+M,x_{21},y_{11},y_{21}\right),\left( x_{11},x_{21},0,y_{21}\right).\)
- 18.
The necessity of this regularity condition was pointed out by Professor R. M. Thrall. If a subset of \(s+m-1\) columns is linear dependent, and these columns span an efficient face of the frontier, then the dimension of this efficient face will be strictly less than \(s+m-1\). Hence, this regularity condition allows us to determine the dimension of a particular efficient face directly from the number of DMUs located on this efficient face. A test of an eventual violation of RC1 can be performed by a MILP program included in Appendix A.
- 19.
Recall the definition in (6.5):
$$ \mathcal{F}^{CCR}\left( \left\{ j\right\} \right) \equiv \left\{\left( u,-v\right) \in \mathcal{P}_{CCR},u^{T}Y_{j}-v^{T}X_{j}=0\right\}.$$ - 20.
An Extended Facet Approach has been proposed by Bessent et al. (1988) by the name “Constrained Facet Analysis.” One problem with the procedure proposed in that paper is that a given subset of DMUs may span a non FDEF. Hence, it may be impossible to reach a FDEF starting from this given subset of DMUs. The existence of non FDEFs could be the reason why their procedure fails to identify FDEFs in 41.4 percents of the reported runs.
- 21.
The so-called Polyhedral Cone-Ratio DEA Models are presented in Charnes et al. (1990) along with an application of one of these models to a set of 48 commercial banks. Using the CCR model in the evaluation of these 48 U.S. commercial banks the authors conclude that “the results were not satisfactory so recourse was made to a polyhedral cone-ratio DEA model with results that passed muster in subsequent reviews with wide experience in banking” (p. 86). The transformational matrix used by the authors to form the cones used in the cone-ratio model consists of optimal virtual multiplier vectors of three CCR extreme efficient “model banks.” One problem related to this application is the following: there is in general no unique dual optimal multiplier for a CCR extreme efficient DMU. Hence, the three CCR extreme efficient model banks will probably contribute to the spanning of many different efficient facets. Three of these efficient facets of full dimension are indicated by the three strict positive normal vectors exhibited in Table 6.3, p. 87 in Charnes et al. (1990). However, if the model banks contribute to the spanning of say six different FDEFs then a set of all six strict positive scaled normal vectors to these FDEFs could/should have been used in the specification of the transformation matrix; or if only a subset is wanted then any subset of these six scaled normal vectors could equally well have been used. In relation to the present paper it is of interest to notice that the extended facet model and the polyhedral cone-ratio model have some common characteristics. In fact, the extended facet MILP program (6.27) can be used to solve the problem related to the application of the cone-ratio model to commercial banks. A cone ratio efficiency analysis based on a transformation matrix consisting of all strict positive optimal virtual multiplier vectors of the three model banks is the result of solving the following MILP program:
$$\begin{aligned}\begin{array}{lllll} \text{max} & u^{T}Y_{j_{o}} & & & \\ s.t. & u^{t}Y_{j}-v^{t}X_{j}+s_{j} & = & 0 & j\in \mathbb{E} \\ & v^{T}X_{j_{o}} & = & 1 & \\ & s_{j}-b_{j}M & \leq & 0 & j\in \mathbb{E} \\ & \sum_{j\in \mathbb{E}}b_{j}-\left\vert \mathbb{E}\right\vert \mathbb{-} \left( s+m-1\right) & \leq & 0 & \\ & b_{j}=0,j\in \left\{ j_{1},j_{2},j_{3}\right\} & & & \\ & b_{j} \text{binary}, s_{j}\geq 0,\forall j\in \mathbb{E},u\geq \varepsilon e,u\in \mathbb{R}_{+}^{s},v\geq \varepsilon e,v\in \mathbb{R}_{+}^{m} & & &\end{array}\end{aligned}$$if we assume the regularity condition RC1. M is a large scalar, \(j_{o}\in \left\{ 1,\ldots,48\right\}\) is the index of the bank being evaluated, \(\mathbb{E}\) is the index set of all the CCR extreme efficient banks among the 48 banks, and \(j_{i}\in \mathbb{E},\) \(i=1,2,3\) is the index of the three model banks.
- 22.
Notice, that regularity condition RC3 is satisfied if we have at least one FDEF with an intercept term being strictly positive.
- 23.
This need of course not to be the case. If the data points included in the Ifile include inefficient data points (points that will turn up as being located in the interior of the convex hull) then these points are declared non-vertex points and are ignored in the generation of the convex hull.
- 24.
See e.g. http://xlr8r.info/mPower/install.html.
References
Aparicio J, Pastor JT (2013) A well-defined efficiency measure for dealing with closest target in DEA. Appl Math Comput 219:9142–9154
Aparicio J, Ruiz AJL, Sirvent AI (2007) Closest targets and minimum distance to the Pareto efficient frontier in DEA. J Prod Anal 28:209–218
Appa G, Argyris N, Williams HP (2006) A methodology for cross-evaluation in DEA, working paper
Asmild M, Hougaard JL, Olesen OB (2013) Testing over-representation of observations in subsets of a DEA technology. Eur J Oper Res 230:88–96
Banker RD, Charnes A, Cooper WW (1984) Some models for estimating technical and scale inefficiencies in data envelopment analysis. Manage Sci 309:1078–1092
Banker RD, Conrad RF, Strauss RP (1986) A comparative application of data envelopment analysis and translog methods: an illustrative study of hospital production. Manage Sci 32(1):230–244
Banker RD, Charnes A, Cooper WW, Maindiratta A (1988) A comparison of DEA and translog estimates of production frontiers using simulated observations from a known technology. In: Dogramaci A, Färe R (eds) Applications of modern production theory. Kluwer, Boston, pp 33–55
Bessent A, Bessent W, Elam J, Clark T (1988) Efficiency frontier determination by constrained facet analysis. Oper Res 36(5):785–795
Briec W, Leleu H (2003) Dual representations of non-parametric technologies and measurement of technical efficiency. J Prod Anal 20:71–96
Brockett PL, Roussau JJ, Wang Y, Zhow L (1997) Implementation of DEA models using GAMS. Research Report 765, University of Texas, Austin
Chambers RG, Mitchell T (2001) Homotheticity and non-radial changes. J Prod Anal 15:31–39
Chambers RG, Chung Y, Färe R (1996) Benefit and distance functions. J Econ Theory 70:407–419
Chambers RG, Chung Y, Färe R (1998) Profit, directional distance functions and Nerlovian efficiency. J Optim Theory Appl 98(2):351–364
Charnes A, Cooper WW, Rhodes E (1978) Measuring the efficiency of decision-making units. Eur J Oper Res 2:429–444
Charnes A, Cooper WW, Rhodes E (1979) Short communication: measuring the efficiency of decision-making units. Eur J Oper Res 3:33–9
Charnes A, Cooper WW, Golany B, Seiford L, Stutz J (1985) Foundations of data envelopment analysis for Pareto-Koopmans efficient empirical production functions. J Econom 30:91–107
Charnes A, Cooper WW, Huang ZM, Rousseau JJ (1989) Efficient facets and the rate of change: geometry and analysis of some Pareto-efficient empirical production possibility sets. CCS Research Report 622, Center for Cybernetic Studies, University of Texas at Austin
Charnes A, Cooper WW, Huang ZM, Sun DB (1990) Polyhedral cone-ratio DEA models with an illustrative application to large commercial banks. J Econom 46(1–2):73–91
Charnes A, Cooper WW, Thrall RM (1991) A structure for classifying and characterizing efficiencies and inefficiencies in data envelopment analysis. J Prod Anal 2:197–237
Cook WD, Seiford L (2009) Data envelopment analysis (DEA)—thirty years on. Eur J Oper Res 192:1–17
Cooper WW, Ruiz JL, Sirvent I (2007) Choosing weights from alternative optimal solutions of dual multiplier models in DEA. Eur J Oper Res 180:443–458
Cooper WW, Ruiz JL, Sirvent I (2011) Choices and uses of DEA weights. In: Cooper WW, Seiford LW, Zhu J (eds) Handbook of DEA, 2 edn, Chap. 4, p 10–9
Doyle J, Green R (1994a) Efficiency and cross-efficiency in DEA: derivations, meaning and uses. J Oper Res Soc 45(5):567–578
Doyle JR, Green RH (1994b) Strategic choice and data envelopment analysis: comparing computeres across many dimensions. J Inform Technol 9:61–69
Färe R, Lovell CAK (1978) Measuring the technical efficiency of production. J Econ Theory 19:150–162
Färe R, Grosskopf S, Lovell CAK (1985) The measurement of efficiency of production. Kluwer- Nijhoff Publisher, Boston
Fukuyama H, Sekitani K (2012) Decomposing the efficient frontier of the DEA production possibility set into a smallest number of convex polyhedrons by mixed integer programming. Eur J Oper Res 221:165–174
Førsund FR, Hjalmarsson L, Krivonozhko VE, Utkin OB (2007) Calculation of scale elsticities in DEA models: direct and indirect approaches. J Prod Anal 28(1/2):45–56
Green RH, Doyle JR, Cook WD (1996) Efficiency bounds in data envelopment analysis. Eur J Oper Res 89:482–490
Grünbaum B (1961) Measures of symmetry for convex sets, Proceedings of the seventh symposium in pure mathematics of the American Mathematical Society, Symposium on Convexity, pp 233–270
Klee VL (1953) Convex sets in linear spaces. Duke Math J 20:33–97
Koopmans TC (1957) Three essays on the state of economic science. Mc. Grawhill, New York
Krivonozhko V, Volodin AV, Sablin IA, Patrin M (2004) Construction of economic functions and calculating of marginal rates in DEA using parametric optimization methods. J Oper Res Soc 55(10):1049–1058
Lang P, Yolalan OR, Kettani O (1995) Controlled envelopment by face extensions in DEA. J Oper Res Soc 46(4):473–491
Lewin AY, Morey RC (1981) Measuring the relative efficiency and output potential of public sector organizations: an application of data envelopment analysis. Int J Policy Anal Inform Syst 5(4):267–285
Olesen OB, Petersen NC (1996) Indicators of ill-conditioned data sets and model misspecification in data envelopment analysis: an extended facet approach. Manage Sci 42:205–219
Olesen OB, Petersen NC (2003) Identification and use of efficient faces and facets in DEA. J Prod Anal 20:323–360
Portela MCAS, Thanassoulis E (2005) Profitability of a sample of Portuguese bank branches and its decomposition into technical and allocative components. Eur J Oper Res 162:850–866
Portela MCAS, Borges PC, Thanassoulis E (2003) Finding closest targets in non-oriented DEA models: the case of convex and non-convex technologies. J Prod Anal 19:251–269
Rockefellar RT (1970) Convex analysis. Princeton University Press, New Jersey
Schrijver A (1986) Theory of linear and integer programming. Wiley, New York
Steuer RE (1986) Multiple criteria optimization. Theory, computation and application. Wiley, New York
Takeda A, Nishimo H (2001) On measuring the inefficiency with the inner-product norm in data envelopment analysis. Eur J Oper Res 133:377–393
Thrall RM (1996) Duality, classification and slacks in DEA. Ann Oper Res 66:109–138.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2015 Springer Science+Business Media New York
About this chapter
Cite this chapter
Olesen, O., Petersen, N. (2015). Facet Analysis in Data Envelopment Analysis. In: Zhu, J. (eds) Data Envelopment Analysis. International Series in Operations Research & Management Science, vol 221. Springer, Boston, MA. https://doi.org/10.1007/978-1-4899-7553-9_6
Download citation
DOI: https://doi.org/10.1007/978-1-4899-7553-9_6
Published:
Publisher Name: Springer, Boston, MA
Print ISBN: 978-1-4899-7552-2
Online ISBN: 978-1-4899-7553-9
eBook Packages: Business and EconomicsBusiness and Management (R0)