A Model for Coupled Outbreaks Contained by Behavior Change

Abstract

Large epidemics such as the recent Ebola crisis in West Africa occur when local efforts to contain outbreaks fail to overcome the probabilistic onward transmission to new locations. As a result, there may be large differences in total epidemic size from similar initial conditions. This work seeks to determine the extent to which the effects of behavior changes and metapopulation coupling on epidemic size can be characterized. While mathematical models have been developed to study local containment by social distancing, intervention and other behavior changes, their connection to larger-scale transmission is relatively underdeveloped. We make use of the assumption that behavior changes limit local transmission before susceptible depletion to develop a time-varying birth-death process capturing the dynamic decrease of the transmission rate associated with behavior changes. We derive an expression for the mean outbreak size of this model and show that the distribution of outbreak sizes is approximately geometric. This allows a probabilistic extension whereby infected individuals may initiate new outbreaks. From this model we characterize the overall epidemic size as a function of the behavior change rate and the probability that an infected individual starts a new outbreak. We find good agreement between the analytical results and stochastic simulations leading to novel findings including critical learning rates that demarcate large and small epidemic sizes.

1 Introduction

Many questions arise during outbreaks of emerging infectious diseases. How transmissible is the new pathogen within the initially exposed population? How fast will it spread to other populations? What must be done to achieve containment? How large will the final epidemic be? These questions and others are amenable to theoretical analysis using dynamic models [12]. Most models of disease transmission, however, assume time constant parameters and do not account for changing human behavior or other interventions. The 2014–2015 West Africa Ebola epidemic illustrates this point. With an $R_0$ around 1.7–3.0 [4, 6, 17] and a population of around 20 million persons [16] in the three primarily affected countries, the final size of an outbreak contained by susceptible depletion [13] would be from 11.7 to 18.8 million persons. In contrast, the actual epidemic size of ${\approx } 30{,}000$ persons is much less than 1 % of this size.

Because standard models admit containment only after the outbreak becomes self-limiting through depletion of susceptible persons, they are inappropriate for making predictions about apparent infections, where self-protective behaviors may be quickly adopted, and in modern societies, where global financial, medical, and logistic resources are rapidly mobilized to contain emerging pathogens like SARS, MERS, and Ebola. But, if behaviors change and resources are quickly mobilized, then why have outbreaks of these emerging pathogens persisted as long as they have? One possible explanation is that behavior change and intervention are local events that occur only around transmission clusters and are not completely efficient, so that while behavior change and intervention act to reduce transmission where it is high, a small fraction of infections escape isolation to seed new outbreaks in spatially or socially adjacent populations. According to this idea, the persistence of the pathogen in the population—and the propensity to transition from outbreak to epidemic proportions—is based on a balance between the ability of the pathogen to spark new outbreaks and the capacity of behavior change and intervention to contain these outbreaks before further spread occurs.

Fig. 1

In the 2014–2015 West Africa Ebola epidemic, the virus spread throughout the administrative units of Liberia during weeks 20 through 40 despite the fact that nation-wide containment measures, including border closure, were put in place beginning in week 30 and the World Health Organization declared the Ebola epidemic to be a Public Health Emergency of International Concern one week later. Here, the cumulative number of cases in each administrative unit is plotted against epidemiological week. These nearly parallel epidemic curves suggest that the same process of outbreak and control was replicated in one county after the next with local interventions and behavior change realized some finite time after cases began accumulating. For instance, approximately the same take-off rate was exhibited by Montserrado as by Grand Cape Mount, despite the fact that their first cases were separated by twelve weeks. Data from the World Health Organization situation reports

Our motivation for this idea comes from the 2014–2015 West Africa Ebola epidemic. For instance, spread among counties in Liberia seems to be consistent with this picture (Fig. 1). Here we see that the epidemic was maintained by a series of outbreaks, each of which recapitulates a common pattern of explosive transmission, followed by a decline in the rate of transmission and eventual containment. Because the transmission process in each county occurs almost independently of the other counties (coupling is primarily important for the initial spark and possibly subsequent reinfections), a single compartmental model cannot accurately represent the associated dynamics. Instead, what is required is a model of coupled epidemics. In the following sections we develop a simple, conceptual model of this process. We imagine an epidemic starting with an outbreak originating at a single location. In contrast to most models, we assume that this outbreak is quickly contained by reductions in transmission. The stochastic nature of transmission when only a small number of persons are infected gives rise to a probability distribution in the outbreak size. Although the outbreak is quickly contained, there is a small chance that the infection is spread to an adjacent population before complete containment is achieved. If this occurs, then the process is repeated until finally no further outbreaks occur. It is this outbreak-of-outbreaks that we call an epidemic. To model this two-scale process, we first propose a simple model for the stochastic dynamics of an outbreak subject to behavior change, for which we obtain the mean outbreak size, denoted M. M is important for three reasons. First, it enables calculation of the chance that a secondary outbreak is caused, which may be iterated until no further outbreaks result. Guided by numerical experiments, we propose to approximate the probability distribution of the number of outbreaks by a geometric distribution. The second role played by the mean outbreak size is to parameterize the geometric distribution of outbreak number. Finally, by summing a random number of outbreaks with the mean size M, we obtain an approximation for the epidemic size, i.e., the size of all outbreaks added together. The accuracy of this approximation is studied through comparison with simulations.

Models that explicitly take account of within and between household transmission have yielded important understanding of the role of host social structure on epidemic development. Part of their success lies in the relatively simple task of enumerating all possible infection statuses of individuals in small households and of assuming a constant hazard of transmission to uninfected cohabitors [2]. In contrast, when attempting to describe connections between local outbreaks (involving population sizes much bigger than households) and larger-scale epidemics against the backdrop of reduced transmission over time, tracking the local outbreak sizes can be challenging. Previous modeling studies of behavior change to limit transmission have generally assumed that transmission dynamics may additionally be slowed by susceptible depletion, e.g., [3, 5, 15]. By instead assuming that behavior changes act before susceptible depletion, birth-death branching process techniques can be utilized. As well as lending analytical tractability, these models likely capture the rapid social distancing and learned risk-averse behavior associated with deadly diseases such as Ebola. In the recent West African outbreak, outbreak sizes were considerably smaller than population sizes (Fig. 1).

2 Final Size of a Single Outbreak with Behavior Change

We assume that local outbreaks are contained by behavior changes over time that act to reduce transmission (rather than the standard assumption of susceptible depletion). We employ a simple time-varying function for the transmission rate, $\beta _0 e^{-\phi t}$. Parameter $\beta _0$ is the intrinsic transmission rate operating in the absence of behavior change, and $\phi$ is the rate of decay in the transmission rate where large values of $\phi$ imply that effective behaviors such as social distancing are adopted rapidly. Because the removal rate $\mu$ is assumed constant then local transmission dynamics are described by

$$\begin{aligned} \frac{dI}{dt}=\beta _0 e^{-\phi t} I - \mu I; \quad \frac{dR}{dt}=\mu I. \end{aligned}$$

(1)

This is a generalized continuous-time birth-death process with time-varying birth rate, as discussed by Kendall [10]. Following Kendall, the mean final size, $R(\infty )$, is given by

$$\begin{aligned} M=1+\int _{0}^{\infty } e^{-\rho (\tau )} \beta (\tau ) d\tau \end{aligned}$$

(2)

where

$$\begin{aligned} \rho (t)= & {} \int _{0}^t (\mu -\beta (\tau )) d\tau \end{aligned}$$

(3)

$$\begin{aligned}= & {} \mu t - \int _{0}^t \beta (\tau ) d\tau \end{aligned}$$

(4)

$$\begin{aligned}= & {} \mu t - \beta _0 \int _{0}^t e^{-\phi t} d\tau \end{aligned}$$

(5)

$$\begin{aligned}= & {} \mu t + \frac{\beta _0}{\phi } [e^{-\phi \tau }]_{0}^t \end{aligned}$$

(6)

$$\begin{aligned}= & {} \mu t + \frac{\beta _0}{\phi } (e^{-\phi t}-1). \end{aligned}$$

(7)

So consequently, we are seeking to solve

$$\begin{aligned} \int _{0}^{\infty } e^{-\mu \tau - \frac{\beta _0}{\phi } (e^{-\phi \tau }-1)} \beta _0 e^{-\phi \tau } d\tau \end{aligned}$$

(8)

$$\begin{aligned} \beta _0 \int _{0}^{\infty } e^{-(\mu +\phi ) \tau - \frac{\beta _0}{\phi }e^{-\phi \tau }} d\tau \end{aligned}$$

(9)

$$\begin{aligned} \beta _0 e^{\frac{\beta _0}{\phi }} \int _{0}^{\infty } e^{-(\mu +\phi ) \tau } e^{ - \frac{\beta _0}{\phi }e^{-\phi \tau }} d\tau . \end{aligned}$$

(10)

Let $z=\frac{\beta _0}{\phi }e^{-\phi \tau }$, then $dz=-\beta _0 e^{-\phi \tau } d\tau$, $d\tau =\frac{-1}{\beta _0}e^{\phi \tau } dz$, $\frac{\phi z}{\beta _0}=e^{-\phi \tau }$, $\mathrm{ln}(\frac{\phi z}{\beta _0})=-\phi \tau$, $\tau =\frac{-1}{\phi }\mathrm{ln}(\frac{\phi z}{\beta _0})$. Now the integral can be written as

$$\begin{aligned} \frac{-\beta _0}{\beta _0}e^{\frac{\beta _0}{\phi }} \int _{\frac{\beta _0}{\phi }}^{0} e^{\frac{\mu +\phi }{\phi }\mathrm{ln}(\frac{\phi z}{\beta _0})} e^{-z} e^{-\mathrm{ln}(\frac{\phi z}{\beta _0})} dz \end{aligned}$$

(11)

$$\begin{aligned} -e^{\frac{\beta _0}{\phi }} \int _{\frac{\beta _0}{\phi }}^{0} \frac{\phi z}{\beta _0}^{\frac{\mu +\phi }{\phi }-1} e^{-z} dz \end{aligned}$$

(12)

$$\begin{aligned} -e^{\frac{\beta _0}{\phi }} \frac{\phi }{\beta _0}^{\frac{\mu +\phi }{\phi }-1}\int _{\frac{\beta _0}{\phi }}^{0} z^{\frac{\mu +\phi }{\phi }-1} e^{-z} dz \end{aligned}$$

(13)

$$\begin{aligned} e^{\frac{\beta _0}{\phi }} \frac{\phi }{\beta _0}^{\frac{\mu +\phi }{\phi }-1} \gamma \left( \frac{\mu +\phi }{\phi },\frac{\beta _0}{\phi }\right) , \end{aligned}$$

(14)

and the final size is

$$\begin{aligned} M=1+e^{\frac{\beta _0}{\phi }} \frac{\phi }{\beta _0}^{\frac{\mu +\phi }{\phi }-1} \gamma \left( \frac{\mu +\phi }{\phi },\frac{\beta _0}{\phi }\right) , \end{aligned}$$

(15)

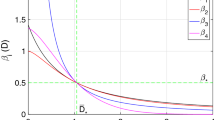
where $\gamma$ is the lower incomplete gamma function. This expression yields some insights into how underlying processes govern outbreak size. Particularly, the left panel of Fig. 2 shows the expected outbreak size to increase greater than exponentially as $\beta _0$ increases. Similarly, the outbreak size initially drops dramatically with learning rate (between 0 and ${\approx } 0.05$ in the right panel of Fig. 2), diminishing as the realized transmission rate becomes small ($\phi > 0.05$). In this figure, the shoulder occurs when $\phi$ is about one fortieth of $\beta _0$.

Fig. 2

Mean outbreak size, M, as a function of $\beta _0$ and $\phi$ (with $\mu$ held at 1.0, $\phi$ is fixed at 0.1 in the left panel, and $\beta _0$ fixed at 2 in the right panel). Note the non-linear functions in semi-log space

Stochastic simulations of Eq. 1, obtained using Gillespie’s direct method, show that outbreak size is “fat-tailed” with high variance, considerable right skew, and a spike at zero (Fig. 3). This suggests the outbreak size distribution might be approximated by a geometric distribution with mean M (Eq. 15). Figure 3 compares 5,000 simulated outbreak sizes with the corresponding approximation (dashed line). The mean of the approximating distribution (solid line) is only slightly larger than the mean of the simulations.

Fig. 3

Histogram of the final outbreak size based on 5000 replicates of the stochastic version of Eq. 1 with $I(0)=1$, $\beta _0=2.0$, $\phi =0.5$ and $\mu =1.0$. The vertical dotted line shows the sample mean oubreak size from these stochastic simulations. The solid vertical line represents the theoretical mean outbreak size (Eq. 15) and the dashed curve is the density of the geometric distribution parameterized with the sample mean outbreak size

3 Global Epidemic Model

To scale up from local outbreaks to epidemics we adopt a probabilistic model in which local outbreaks are connected by movement of infected individuals among communities. In general, we assume that the number of uninfected communities is large so that the chance that an infected individual sparks an outbreak in another community may be represented by a small constant $0 < \varepsilon \ll 1$. Let $p_x$ be the probability mass function for an outbreak of size x. Since the probability that an individual doesn’t spark a secondary outbreak is $1-\varepsilon$, the probability that an outbreak of size x fails to spark a secondary outbreak will be $(1- \varepsilon )^x$ by an assumption of independence. The probability that there is an outbreak of size x and that it fails to spark any secondary outbreaks is therefore $p_x(1-\varepsilon )^x$. By enumeration of all possible outbreak sizes, the probability that an outbreak of unknown size will spark at least one secondary outbreak is

$$\begin{aligned} \alpha = 1- \sum _{x=1}^\infty p_x(1-\varepsilon )^x. \end{aligned}$$

(16)

With $\varepsilon \ll 1$, we assume that each outbreak sparks, at most, only one secondary outbreak.

Let $j = 1, 2, 3, ..., N$ index the local outbreaks so that N is the total number of local outbreaks. The probability that the first outbreak is also the last one is just $p(N=1) = 1- \alpha$. By contrast, the probability that the first outbreak gives rise to a secondary outbreak (with probability $\alpha$) and that the second outbreak fails to give rise to a third (with probability $1-\alpha$) is $p(N=2) = \alpha (1-\alpha )$. Proceeding to $j=3$, the probability that both outbreaks one and two give rise to a secondary outbreak and that the third outbreak is the last yields $p(N=3) = \alpha ^2(1-\alpha )$. By induction, we see that the general rule is given by

$$\begin{aligned} f(m) = p(N=m) = \alpha ^{m-1}(1-\alpha ). \end{aligned}$$

(17)

The next challenge is to ascertain the total number of cases in these m outbreaks. Let $X_j$ be the random number of cases in the jth outbreak. The total number of cases in the epidemic will be the sum of cases in the local outbreaks, i.e.,

$$\begin{aligned} Y_m = \sum _{j=1}^m X_j. \end{aligned}$$

(18)

Since the $X_j$ are independently and identically distributed according to distribution $p_x$, it follows that the distribution of $Y_m$ is just the m-fold convolution of $p_x$, denoted $p_x^{m*}$. The probability that there are exactly m outbreaks and that these give rise to Y cases is

$$\begin{aligned} p_y = p_x^{m*}f(m). \end{aligned}$$

(19)

Using the notation of Johnson et al. [8], we have the following re-parameterization for the distribution of outbreak sizes.

$$\begin{aligned} M = (1-p)/p \rightarrow p = 1/(M+1), \end{aligned}$$

(20)

$$\begin{aligned} P = (1-p)/p = M, \end{aligned}$$

(21)

and

$$\begin{aligned} Q = 1/p = M+1. \end{aligned}$$

(22)

If k outbreaks are summed, the result is negative binomially distributed with parameters k and P. Let k be the number of non-primary outbreaks. Applying the same rationale used to arrive at Eq. 17, we obtain $P(k=0) = 1-\alpha = a$ and in general $P(k=n) = (1-a)^na$. So, the number of non-primary outbreaks is a geometric distribution with parameter $p=a$.

Following Johnson et al. [8], the distribution formed by taking a negative binomial with k drawn from a geometric distribution with parameters $Q'$ and $P'$ is also a geometric distribution with parameter $QQ'-P'$. Identifying parameters in Eq. 17, we have $Q'=1/(1-\alpha )$ and $P'=\alpha Q'$ yielding $Q=(M+1)(\frac{1}{1-\alpha }) - \frac{\alpha }{(1-\alpha )}$. Expanding to obtain the unconditional total epidemic size distribution, we have

$$\begin{aligned} P(Y=y) = \pi (1-\pi )^{y-1}, \end{aligned}$$

(23)

where

$$\begin{aligned} \pi =\left( (M+1)(\frac{1}{1-\alpha }) - \frac{\alpha }{(1-\alpha )} \right) ^{-1}. \end{aligned}$$

(24)

This simplifies to

$$\begin{aligned} P(Y=y) = \frac{(1-\alpha )(M/(M+1-\alpha ))^{y-1}}{M+1-\alpha } \end{aligned}$$

(25)

with expected value

$$\begin{aligned} 1/\pi = (M+1)\left( \frac{1}{1-\alpha }\right) - \frac{\alpha }{(1-\alpha )}. \end{aligned}$$

(26)

Fig. 4

Example output from model simulating coupled outbreak dynamics initiated by a single individual. The local outbreak dynamic parameters are $\beta _0=3.0$, $\mu =1.0$ and $\phi =0.1$. The per capita rate of sparking a new outbreak is $\varepsilon =0.25$. In this example, there are 16 local outbreaks before the process stops

4 Comparison with Numerical Results

This derivation of Eq. 25 relies on approximations for the probability of a secondary outbreak given an outbreak of unknown size (Eq. 16) and the distribution of outbreak sizes (assumed to be approximated by a geometric distribution), as well as the assumption that outbreak number and outbreak sizes are independent. We evaluated these assumptions by comparing Eq. 25 with numerical simulations in which chains of outbreaks were probabilistically generated by linking individual outbreaks simulated as in Sect. 2. Figure 4 shows an example solution that is visually similar to the data on Ebola shown in Fig. 1. Figure 5 compares the mean and 99th percentile of epidemic size for the approximation and simulated results over a range of $\varepsilon$ and $\phi$. The two solutions are similar to order of magnitude for most combinations of these parameters, failing primarily when $\phi$ becomes very small.

Fig. 5

Left-hand panels (top to bottom) show the predicted mean epidemic size, Eq. 26, the simulated mean epidemic size and the difference between the two as a function of model parameters $\varepsilon$ and $\phi$. Right-hand panels show analogous information for the 99th percentile of epidemic sizes. Constant model parameters are $\beta _0=2.0$ and $\mu =1.0$. Epidemic sizes are simulated from 5000 replications. Contours are indicated by white lines

5 Discussion

The goal of this work has been to develop a relatively simple model that nevertheless provides valid insight into the effects of behavior change and coupling among local populations on the final size of potentially extensive outbreaks. Such processes are invariably at work in outbreaks of novel pathogens that ultimately affect large, distributed populations, notably outbreaks of Ebola [17], SARS [11], and MERS [14]. The model we developed considers epidemics to consist of multiple coupled outbreaks where outbreak trajectories are contained by local behavior response. Containment is counteracted with the potential of each local outbreak to spark secondary outbreaks through the movement of infected persons so that the final epidemic size reflects the tension between these two processes.

Focusing first on the distribution of outbreak sizes, this work shows that initially supercritical outbreaks that are intrinsically contained through a decline in the transmission rate (assumed to be exponential with time since the outbreak began), give rise to a fat-tailed distribuion of local outbreak sizes. Moreover, the outbreak size distribution changes in a strongly nonlinear fashion with respect to both the initial rate of transmission and the learning rate. Approximating this distribution by a geometric distribution with mean given by Eq. 15 enables one to investigate the tension between containment and expansive spread, i.e., epidemics. Figure 5 shows there to be a large region of the upper left of the $\varepsilon - \phi$ parameter space in which epidemics (i.e., extensive outbreaks with multiple communities affected) are exceedingly unlikely. To the right hand of each panel in Fig. 5, i.e., as $\varepsilon \rightarrow 1$, the outbreak size contours turn up rapidly, beyond which movement of infected individuals is so common that the epidemic is effectively well mixed. Outside this range, the outbreak size contours are practically horizontal, illustrating very little dependence on the rate of individual movement so that learning—and the propensity to self-containment—becomes the much more important process. We are unaware of prior results suggesting this transition between epidemics dominated by movement and epidemics dominated by learning.

The super-exponetial scaling of the outbreak size shown in Fig. 2 is recapitulated in the distribution of outbreak sizes. Thus, for instance, as one moves from the top of each panel in Fig. 5 the contours become closer together. Similarly, the fat-tail in the outbreak size distribution (Fig. 3) propagates to the epidemic size distribution. This is perhaps most easily seen by noting that there is an approximately one logarithm displacement between the contours for the average epidemic size and the 99th percentile in Fig. 5. Thus, for an average epidemic size of 1,000, it is not improbable for an epidemic of 10,000 to be realized. Comparison of the approximate analytic results in the first row of Fig. 5 with the exact results from stochastic simulation in the second row shows that although the approximation comes at a small cost in terms of bias, these qualitative conclusions are robust to the range of assumptions required for their solution, particularly the assumption that the zero-inflated distribution of outbreak sizes can be reasonably approximated by a geometric distribution.

Other assumptions we have made include that the probability any local outbreak sparks more than one secondary outbreak is negligible and that there is no effect of susceptible depletion. The first of these assumptions biases downward our expression for the total number of outbreaks (Eq. 17). This bias becomes more severe as $\varepsilon \rightarrow 1$, i.e., to the right in each panel of Fig. 5, which would further differentiate our two modes for epidemic expansion. The second issue is of negligible consequence unless the total epidemic size tends to be large relative to the population size (precisely what containment prevents) or where the contacts among susceptible persons are highly structured. While there has been a great deal of theory about this latter condition [9], whether it obtains in generalized epidemics like Ebola remains poorly understood. Additionally, the modeling approach adopted here may admit other assumptions (particularly concerning the underlying distribution of local outbreak sizes) and extensions, including the seeding of multipe new outbreaks from a single outbreak and a time-varying “death” rate in the birth-death process, representing more rapid treatment/isolation with increasing experience.

Multiscale modeling of infectious diseases remains a significant mathematical and computational challenge [7]. The simplifying, plausible assumptions made here have allowed us to relate ultimate epidemic size to the rate at which transmission at a local scale is reduced by behavior change and the probability that a new outbreak is seeded elsewhere before local containment. These analytical results are achieved even though the model does not describe a stationary process and illustrates the value of combining modeling approaches, here the outcome of a potentially large number of branching processes accumulated via convolution. One of the key results is that epidemic size grows faster than exponential with decreasing behavioral learning rate, suggesting that there are critical rates above which behaviors acting to reduce transmission will dramatically reduce the overall number of persons infected during a series of outbreaks. Qualitatively, this phenomenon points to a potential connection between the approach undertaken here and random network modeling [1] where the addition of a few links can lead to explosive percolation suddenly connecting a large proportion of nodes. Practically, it underscores the importance of early response to epidemic containment.