Abstract
This article surveys the development of observational understanding of the interior rotation of the Sun and its temporal variation over approximately forty years, starting with the 1960s attempts to determine the solar core rotation from oblateness and proceeding through the development of helioseismology to the detailed modern picture of the internal rotation deduced from continuous helioseismic observations during solar cycle 23. After introducing some basic helioseismic concepts, it covers, in turn, the rotation of the core and radiative interior, the “tachocline” shear layer at the base of the convection zone, the differential rotation in the convection zone, the near-surface shear, the pattern of migrating zonal flows known as the torsional oscillation, and the possible temporal variations at the bottom of the convection zone. For each area, the article also briefly explores the relationship between observations and models.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The internal rotation of the Sun is intimately related to the processes that drive the activity cycle. Brown et al. (1989) stated that, “Knowledge of the internal rotation of the Sun with latitude, radius, and time is essential for a complete understanding of the evolution and the present properties of the Sun,” and this remains true today.
The Sun rotates on its axis approximately once every 27 days; however, the rotation is not uniform, being substantially slower near the poles than at the equator. This superficial aspect of the solar differential rotation was well known from sunspot observations as early as the 17th century. However it is only within the last 30 years that it has become possible to observe the rotation profile in the solar interior, and mostly within the most recent solar cycle that its subtle temporal variations have become evident. Helioseismology — the study of the waves that propagate within the Sun and the inference from their properties of the solar interior structure and dynamics — is the most important tool we have to measure this internal rotation.
In this review, we start by introducing some of the basic concepts of helioseismology (Section 2) and the inversion problem (Section 3) as it applies to the internal solar rotation. Next, after a brief historical overview (Section 4) of the observations, we consider what we have learned from helioseismology about the rotation profile and its variation with depth.
We consider first the time-invariant part of the solar rotation profile. The main features of interest are (Figure 1):
-
1.
the radiative interior and core, which appear to rotate approximately as a solid body, though the innermost core may behave differently (Section 5);
-
2.
the tachocline, a relatively thin zone of shear between the differentially rotating convection zone and the radiative interior, which is believed to play an important role in the solar dynamo (Section 6);
-
3.
the differential rotation in the bulk of the convection zone (Section 7); and
-
4.
the subsurface shear layer between the fastest-rotating layer at about 0.95 R⊙ and the surface (Section 8).
A section through the interior of the Sun, showing the contours of constant rotation and the major features of the rotation profile, for a temporal average over about 12 years of MDI data. The cross-hatched areas indicate the regions in which it is difficult or impossible to obtain reliable inversion results with the available data.
We will consider each of these in turn, working outwards from the core to the surface, and then discuss the time-varying part of the rotation — the torsional oscillation (Section 9) and the possible variations at the base of the convection zone (Section 10). We attempt to place the observations in the context of models; however, this is a review from an observer’s point of view, and an exhaustive examination of the models themselves is beyond its scope.
2 Acoustic Modes
2.1 Introduction
The raw data of helioseismology consist of measurements of the photospheric Doppler velocity — or in some cases intensity in a particular wavelength band — taken at a cadence of about one minute and generally collected with as little interruption as possible over periods of months or years; the measurements can be either imaged or integrated (“Sun as a Star”). An overview of the observation techniques can be found in Hill et al. (1991a). Figure 2 shows a typical single Doppler velocity image of the Sun, and Figure 3 a portion of an l = 0 time series, derived by averaging the velocity over the visible disk for each successive image in a set of observations. The five-minute period and the rich beat structure are clearly visible in the time series. For an example of an integrated-sunlight spectrum from a long series of observations, see Figure 15.
A single Doppler velocity image of the Sun from one GONG [Global Oscillation Network Group] instrument (left), and the difference between that image and one taken a minute earlier (right), with red corresponding to motion away from, and blue to motion towards, the observer. The shading across the first image comes from the solar rotation.
As was first discovered by Deubner (1975), the velocity or intensity variations at the solar surface have a spectrum in k − ω or l − ν space that reveals their origin in acoustic modes propagating in a cavity bounded above by the solar surface and below by the wavelength-dependent depth at which the waves are refracted back towards the surface. These “p modes” can be classified by their radial order n, spherical harmonic degree l, and azimuthal order m; as discussed, for example, in Section 2.2 of Birch and Gizon (2005), the radial displacement of a fluid element at time t, latitude θ and longitude ϕ can be written in the form
where ξnlm is the radial eigenfunction of the mode with frequency ωnlm and \(Y_{l}^{m}(\theta,\phi)\) is a spherical harmonic. As seen in Figure 4, the power in the spectrum falls along distinct “ridges” in the l − ν plane, each ridge corresponding to one radial order. The modes making up the n = 0 ridge are the so-called f modes, which are surface gravity waves. The p modes, so called because their restoring force is pressure, are excited at the surface and have their largest amplitudes there. Another class of modes, the g modes with gravity as the restoring force, excited in the core and with amplitudes vanishing at the surface, are hypothesized to exist but have so far not been definitely observed (Section 5.9).
The longer the horizontal wavelength — and the lower the degree — the more deeply the modes penetrate, with the radial l = 0 mode going all the way to the core of the Sun (but providing no rotational information), while modes with l ≥ 200 or so penetrate only a few megameters below the surface and are generally too short-lived to form global standing waves; these are the modes used for local helioseismology. The lower turning point radius, rt, is a monotonic function of the phase speed ν/L, where \(L = \sqrt {l(l + 1)} \approx l + 1/2\), as shown in Figure 5. The varying penetration depth with degree, as illustrated in Figure 6, makes it possible to deduce the rotation and other properties of the solar interior profile as a function of depth.
Lower turning point of acoustic modes as a function of phase speed ν/L, based on Model S of Christensen-Dalsgaard et al. (1996).
Locations of modes in the l, ν plane for a typical MDI mode set. The colored shading represents the radial regions in which the modes have their lower turning points; the core, r ≤ 0.2 R⊙, the radiative interior, 0.2 ≤ r/R⊙ ≤ 0.65, the tachocline, 0.65 ≤ r/R⊙ ≤ 0.75, the bulk of the convection zone, 0.75 ≤ r/R⊙ ≤ 0.95, and the near-surface shear layer, r/R⊙ ≥ 0.95; the dashed line on the lower right corresponds to r/R⊙ = 0.99.
The lowest-degree modes are observed in integrated sunlight, but for the purposes of measuring the interior rotation profile we are mostly concerned with what are termed medium-degree (l ≤ 300) modes, which can be observed with imaging instruments of relatively modest (≈ 10 arcsec) resolution. The power in the modes peaks at about 3 mHz, or a period of 5 minutes; useful measurements can be made for modes between about 1.5 and 5 mHz, with the frequency determination becoming more challenging at the extremes due to signal-to-noise issues and, at the high-frequency end, to the increasing breadth of the peaks.
2.2 Differential rotation and rotational splitting
The Sun’s rotation lifts the degeneracy between modes of the same l and different m, resulting in “rotational splitting” of the frequencies as waves propagating with and against the direction of rotation (prograde and retrograde) have higher and lower frequencies. To first order, the splitting δνm,l ≡ ν−m,l − ν+m,l is proportional to the rotation rate multiplied by m.
Figure 7 shows a typical m − ν acoustic spectrum of GONG data at l = 100. The effect of the rotation causes the ridges at each n to slant away from the ν = 0 axis; closer examination reveals that the ridges have an S-curve shape that arises from the differential rotation, and also shows the ridge structure due to leakage, which will be discussed below in Section 2.3.
Because modes of different m values sample different latitude ranges, with the sectoral (∣m∣ = l) modes confined to a belt around the equator and the zonal or m = 0 modes reaching to the poles, as illustrated in Figure 8, we can measure the rotation as a function of latitude.
A given (n, l) multiplet consists of 2l + 1 frequency measurements if each (l, m) spectrum is analyzed separately, though some fraction of these frequencies may be missing in any given data set. This amount of data was somewhat unwieldy in the early days of helioseismology. It is therefore common to express νnl(m) as a polynomial expansion, for example,
where the basis functions are polynomials related to the Clebsch-Gordan coefficients \(C_{j0lm}^{lm}\) by
(Ritzwoller and Lavely, 1991). Indeed, in many analysis schemes coefficients of the expansion are derived by fitting directly to the acoustic spectrum and the individual frequencies are not measured. This approach can improve the stability of the fits, perhaps at the cost of imposing systematic errors. Early work used Legendre polynomials; however, most modern work uses either Clebsch-Gordan coefficients or the Ritzwoller-Lavely formulation, which come closer to being truly orthogonal for the solar rotation problem. Only the odd-order coefficients encode the rotational asymmetry, while the even-order coefficients contain information about the structural asphericity. Roughly speaking, the a1 coefficient describes the rotation rate averaged over all latitudes, and the a3 and higher coefficients describe the differential rotation.
2.3 Spherical harmonics and leakage
Spherical harmonic masks are used to separate the contributions from modes of different degree and azimuthal order into complex time series, which can then be transformed to acoustic Fourier spectra.
The radial component of the velocity at the solar surface from a mode with a given degree l, azimuthal order m, and radial order n is given by
where Re[…] denotes the real part, ϕ is longitude, and θ is latitude (see, for example, Schou and Brown 1994a). The masks used separate the different spherical harmonics take the form
where A is an apodization function and \(\rho \equiv \sqrt {{{\cos}^2}\theta + {{\sin}^2}\theta {{\sin}^2}\phi}\) represents the fractional distance from disk center in the solar image. The line-of-sight projection factor is \(V = \sqrt {1 - {\rho ^2}}\).
Because only part of the solar surface is visible at any time, the masks are not completely orthogonal and the modes “leak” into neighboring spectra. This leakage complicates the analysis and can cause systematic errors in the measured frequencies if it is not correctly taken into account. For a detailed discussion of the calculation of the so-called “leakage matrix,” see Schou and Brown (1994a) and Hill and Howe (1998). Briefly, the leakage matrix element s(l, m, l′, m′) for leakage from the l′, m′ mode to the l, m spectrum can be computed as
Symmetry properties in this expression lead to some simple exclusion rules; for example, leaks with odd ∣δl + δm∣ (where δm ≡ m − m′ and δl ≡ l − l′) are not allowed.
One example of the importance of the leakage is in the contribution of the so-called m-leaks (δl = 0, δm = ±2) to the estimation of low-degree splittings. As pointed out, for example, by Howe and Thompson (1998), these leaks are strongest for small ∣m∣; they are also asymmetrical, especially for ∣m∣ = l, where the m = l peak has an m = l − 2 leak on one side and no counterbalancing m = l + 2 leak on the other. Especially for l = 1, this can introduce a serious systematic error into the estimate of the splitting if not properly accounted for.
Leakage also means that integrated-sunlight instruments (which effectively use the l = 0 mask) can detect modes of 0 ≤ l ≤ 5, though the sensitivity falls off rapidly for l > 1. All these modes appear in a single acoustic spectrum; the instruments are sensitive to odd-m modes for odd l and to even-m modes for even l, with the sectoral, or ∣m∣ = l, modes most strongly detected.
In general, the leakage has effects throughout the acoustic spectrum, but the most deleterious effects arise when the leaks cannot be resolved from the target peaks. This occurs for m-leaks at frequencies above about 2 mHz; for higher-degree modes the leakage between modes of adjacent l becomes a problem, as the ridges become both broader, and more closely spaced in frequency, at around l = 150. Beyond this point the peaks cannot be fitted independently, and some modeling of the leakage is essential in order to estimate the mode parameters.
2.4 Estimating rotation properties directly from coefficients
It is possible to make some inferences about the rotation profile without carrying out a full-scale inversion. Simple examination of the odd-order coefficients, sorted by the lower turning-point radius of the modes, reveals the existence of the near-surface shear, the differential rotation within the convection zone, and a discontinuity in the differential rotation at the base of the convection zone, as shown in Figure 9. More sophisticated analysis is also possible. For example, Wilson and Burtonclay (1995) gave approximate expressions for the rotation profile at different latitudes as sensed by a particular n, l multiplet, \({\bar \Omega ^{nl}}\), as follows:
These estimates, where the subscripts on the LHS refer to the latitude in degrees, are noisy for individual multiplets, but Wilson and Burtonclay (1995) were able to build up a picture of the internal rotation from BBSO data by forming cumulative averages with the input data sorted in ascending order of ν/L.
a1 (top) and a3 (bottom) coefficients for (left) 1986 BBSO observations, (middle) 108 days of GONG observations in 1996, (right) the mean of 35 consecutive 108-day periods of GONG observations from 1995–2005, plotted as a function of phase speed with the turning point radius marked on the upper axis.
3 Inversion Basics
Various inversion techniques are used to infer the internal rotation profile from the observed frequency splittings. The aim of the inversion procedure is to form linear combinations of the data that give well-localized inferences of the rotation at a particular location within the Sun. We will discuss only linear inversion methods, as non-linear approaches are not needed for the relatively low velocities involved in the global rotation.
3.1 The inversion problem
The basic 2-dimensional rotation inversion problem can be stated as follows: we have a number M of observations di, from which we wish to infer the rotation profile Ω(r, θ) where r is distance from the center of the Sun, and θ is (conventionally) colatitude. Each datum is a spatially weighted average of the rotation rate:
where R⊙ is the solar radius, the error term ε corresponds to the noise and measurement error in the data, and K is a model-dependent spatial weighting function known as the kernel (Hansen et al., 1977; Cuypers, 1980). For the two-dimensional rotation inversion, the radial part is related to the eigenfunction of the mode and the latitudinal part to the associated Legendre polynomial; Schou et al. (1994) give the expression for the kernel as
where
x = cos θ, L2 = l(l + 1), ξnl is the radial displacement for the eigenfunction of the mode, L−1ηnl is the horizontal displacement, and ρ(r) is the density (see Figure 10 for illustrations of sample kernels).
The aim of the inversion is to find
where (r0, θ0) is the location at which the inferred rotation rate \(\bar{\Omega}\) is to be found and the ci are the coefficients to be used to weight the data; the inversion process can be thought of as the search for the best values for these coefficients.
3.2 Averaging kernels
By substituting Equation (11) into the RHS of Equation (14) we obtain
where
is the averaging kernel for the location (r0, θ0). The averaging kernels are independent of the values of the data. However, because the uncertainties in the data are used to weight the inversion calculation that generates the coefficients ci, as described below in Sections 3.4 and 3.5, these do enter indirectly into the averaging kernels. The averaging kernels also depend on which modes are present in the input data set. They provide a useful tool for assessing the reliability of an inversion inference from a particular mode set (see, for example, Schou et al., 1992, 1994).
3.3 Inversion errors
If the errors on the input data are uncorrelated and properly described by a normal distribution whose width corresponds to the quoted uncertainty σi, the formal uncertainty on the inferred profile is given by
In the (usually unrealistic) case where the errors on the input data are all equal, we can write
where the “error magnification” is given by
As discussed, for example, by Christensen-Dalsgaard et al. (1990), a quantitative choice of regularization parameters can then be made by finding the “knee” of a tradeoff curve where the error magnification is plotted against the width of the averaging kernel. However, in the two-dimensional case this does not always give a clear result, and this formulation of the error magnification is not very useful for modern data sets where the uncertainties on the parameters are anything but uniform. Instead, one can consider the uncertainty on the inferred quantity at a particular location.
Even when the errors on the input data are uncorrelated, the errors on the inferred profile will not be, as discussed by Howe and Thompson (1996). (As a simple way to understand this, consider the case where one measurement is significantly “off”, this will affect the inferred profile at every location where the inversion coefficient ci for that datum is non-zero.) In the one-dimensional case, the correlation between the errors for two points r0 and r1 is given by
this can easily be generalized to the two-dimensional case. Howe and Thompson (1996) found that the spatial scale over which the inversion errors are significantly correlated is usually similar to that for the averaging kernels, though for some cases where the inversion parameters have been badly chosen the results can be correlated over long distances even when the averaging kernels appear well formed.
Error correlations by definition should not distort the inferred profile beyond the distribution predicted by the formal uncertainty on the inferences, provided always that the input uncertainties are correct. However, the finite width of averaging kernels also gives rise to a systematic error that can be much larger. Consider, for example, the case where a thin shear layer is not resolved; then all the estimated rotation rates on one side of the shear could be underestimated, and those on the other side overestimated, by several times the formal uncertainty. Such systematic errors and their relationship to the averaging kernels have been discussed, for example, by Christensen-Dalsgaard et al. (1990).
Gough et al. (1996) pointed out that it is not sufficient for the rotation rates at two locations to have non-overlapping errors as calculated in Equation (17), and described a method for increasing the error estimates on inversions to allow truly significant differences between the inferred rotation rate at different locations to be determined. This method, however, has not been widely used.
Because the input data are noisy and of finite resolution, the inversion problem does not have a unique solution; there will always be a tradeoff between noise and good localization. Two widely-used approaches to balancing these criteria are “regularized least squares” (RLS) and “optimally localized averaging” (OLA).
3.4 Regularized least squares
The RLS approach to the inversion problem is to find (essentially through a least-squares fit) the model profile that best fits the data, subject to a smoothness penalty term, or regularization. More regularization — a larger weighting for the penalty term — results in poorer spatial resolution (and potentially more systematic error) but smaller uncertainties. In one such implementation (Schou et al., 1994), we minimize
with μr and μθ being the radial and latitudinal tradeoff parameters. The RLS inversion has the advantages of being computationally inexpensive and always (thanks to the second-derivative regularization, which amounts to an a priori assumption of smoothness) providing some kind of estimate of the quantity of interest even in locations that are not, strictly speaking, resolved by the data. In this method, the averaging kernels \({\cal K}\) can (but need not be) calculated from the coefficients in a separate step. They are not guaranteed to be well localized, though they are forced to have a center of mass at the specified location r0,θ0. Figure 11 illustrates typical averaging kernels for a 2dRLS inversion of an MDI data set.
Averaging kernels for a typical RLS inversion of MDI data, for target latitudes 0 (a), 15 (b), 30 (c), 45 (d), 60 (e), and 75 (f) degrees as marked by the dashed radial lines, and target radii 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 0.95, 0.99 R⊙ indicated by colors from blue to red as denoted by the dashed concentric circles. Contour intervals are 5% of the local maximum value closest to the target location, with dashed contours indicating negative values.
3.5 Optimally localized averaging
In the Subtractive OLA (SOLA) approach (Backus and Gilbert, 1968, 1970), the minimization is applied to the difference between the actual averaging kernels \({\cal K}\) and a target kernel \({\cal T}\), for example a 2-dimensional Gaussian or Lorentzian function. In this case (Pijpers and Thompson, 1992, 1994) the function minimized is
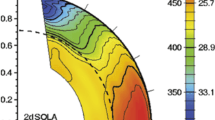
Both the tradeoff parameter λ and the radial and latitudinal resolution of the inversions must be chosen before running the inversion. If the choice of target kernel is poor — too narrow or too wide for the quantity and quality of the data — the reliability of the inversion will suffer. In OLA inversions, setting target locations outside the regions that can be resolved using the data will result in averaging kernels displaced from their targets, and this should be taken into account when interpreting the results. Figure 12 illustrates typical averaging kernels for a 2d SOLA inversion of an MDI data set.
As Figure 11, for a SOLA inversion.
Another approach, older, and more computationally expensive, is the Multiplicative OLA (MOLA) described by Pijpers and Thompson (1992, 1994). Here, no target form is imposed on the averaging kernel, but it is multiplied by a term which penalizes large values away from the target location.
3.6 Other methods
Alternatives to full 2-dimensional inversions are the so-called “1.5-dimensional” approach, in which 1-dimensional radial inversions are carried out separately for each of the coefficients describing the latitudinal rotation variation, and “1d⊗1d” inversions in which the radial and latitudinal variations of the rotation rate are integrated separately. For details of many of these methods, please see Schou et al. (1998) and references therein.
3.7 Limitations
It is important to bear in mind the limitations of the inversion process when considering the results. The deepest and shallowest depths that can be resolved, for example, are limited by the deepest and shallowest turning-point radii of the available modes. The rotational splitting at a given m is to first order proportional to the rotation rate multiplied by ∣m∣; since the only mode whose latitudinal kernel reaches the pole is the m = 0 mode, which has no longitudinal structure and so can convey no rotational information, and the modes of small ∣m∣/l have only a few nodes around the equator and hence have low sensitivity to the rotation, the 2d inversion becomes progressively less reliable at high latitudes. Furthermore, since only modes of relatively low degree (l ≤ 20) penetrate into the radiative interior, the latitudinal resolution in this region is quite poor and becomes progressively worse with depth; radial resolution also becomes coarser in the interior. The practical effects of such limitations can be assessed by careful inspection of the averaging kernels, or by performing forward-calculation tests in which the averaging kernels are convolved with known test profiles.
Another point to bear in mind when considering inversion results is that the inversion can measure only the north — south symmetric part of the profile; any asymmetry between the hemispheres is averaged out. The inversions are also insensitive to meridional motions. Some information on hemispheric differences can be obtained using the techniques of local helioseismology, as reviewed by Birch and Gizon (2005), but these techniques, using high-degree modes, are mostly sensitive only to the outer layers of the Sun.
4 Observations: A Brief Historical Overview
Systematic helioseismic observations stretch back nearly 30 years, as illustrated in the schematic chart in Figure 13.
Schematic time line of helioseismic observations in the last three solar cycles (top panel), with the filled part of each bar representing approximate duty cycle, plotted on the same temporal scale as the butterfly diagram (bottom panel) of the gross magnetic field strength from Kitt Peak observations.
Prior to the identification of global low-degree modes by Claverie et al. (1979), observing runs were usually short and carried out at a single site. However, the advantages of more extended observations (to obtain better frequency resolution), and of observations not modulated by the day-night cycle, were soon recognized. Grec et al. (1980), Duvall Jr and Harvey (1984), and Duvall Jr et al. (1984, 1986) carried out important observations at the South Pole during the Austral summer, but for long time series it is more practical to observe either from a network of sites spaced around the world, or from space.
Some of the first long-term sets of low-degree observations came from the Active Cavity Irradiance Monitor (ACRIM) experiment (Woodard and Noyes, 1985, 1988) aboard the Solar Maximum Mission spacecraft, which took helioseismic measurements in 1980 and 1984–1985, the Mark I instrument in Tenerife (Pallé et al., 1989), and the precursors of the Birmingham Integrated Solar Network (BiSON) (Elsworth et al., 1990a). Meanwhile, resolved-Sun observations were carried out at the South Pole by Duvall and collaborators, and by various other observers in the USA; these observations will be discussed in more detail later.
Libbrecht and Woodard (1990) observed the medium-degree modes from Big Bear Solar Observatory (BBSO) in the 1986–1990 rising phase of solar cycle 22. The first observations from widely separated sites were carried out by the Birmingham/Tenerife group in 1981 (Claverie et al., 1984), and by 1992 the six-station BiSON network was complete; it has been operating ever since. Another network of integrated-sunlight instruments, the French-based IRIS (Fossat, 1995), operated from 1989–2003.
The Global Oscillation Network Group (GONG) (Harvey et al., 1996) has been collecting continuous, high-duty-cycle observations of the medium-degree p modes since 1995, using a six-station worldwide network, and the Michelson Doppler Imager (MDI) instrument (Scherrer et al., 1995) aboard the SOHO spacecraft has been in operation since 1996, so that these two projects have essentially complete coverage of solar cycle 23. SOHO also carries instruments dedicated to the study of low-degree oscillations; LOI (Luminosity Oscillations Imager) (Fröhlich et al., 1995), and GOLF (Global Oscillations at Low Frequencies) (Gabriel et al., 1995). This wealth of high-quality data has given us the opportunity to study the solar interior rotation and its solar-cycle changes in more detail than ever before.
Also worth noting are the LOWL-ECHO project (Tomczyk et al., 1993), which made medium-degree observations from one or two sites from 1994 to 2004, and the high-degree Taiwanese Oscillations Network (Chou et al., 1995) deployed over the 1993–1996 period.
All these observations will be considered in more detail as we proceed to examine the results pertaining to the interior rotation.
5 The Core and Radiative Interior
5.1 The oblateness controversy
Interest in the rotation of the deep solar interior predates systematic helioseismic observation. One other possible diagnostic of the internal rotation is provided by the solar oblateness; because the Sun is not a solid body, both gravitational and rotational effects cause a very slight flattening. The lowest-order term in this effect is related to the quadrupole moment J2; confusingly, the next-highest term, J4, is sometimes called octopole and sometimes hexadecapole. According to Rozelot and Rösch (1997), who give a useful review of attempts to measure the solar oblateness, for a non-rotating Sun the oblateness Δr = req − rpol is given by
where req and rpol are the equatorial and polar radii, respectively, and r0 is the radius of the best sphere passing through req and rpol. If there is an additional δr contribution from the surface rotation this expression becomes
The units of δr and Δr are conventionally arc ms.
Dicke (1964) noted that, if the Sun were oblate because of fast interior rotation, the effect on its gravitational potential might destroy the agreement between the predictions of General Relativity and the observations of the perihelia of the inner planets, (specifically Mercury, though Venus could in principle experience a smaller effect) potentially leaving room for alternate theories of gravitation. Dicke sets out to determine the solar oblateness from ground-based measurements — a challenging endeavor that produced controversial results. Models (e.g., Brandt 1966) suggested that the interior of the Sun could still be spinning at the rapid rate at which it originally formed, while the exterior had been slowed down by the torque of the solar wind. (As will be further discussed in Section 6, in the absence of direct observations of the solar interior the picture of solar interior dynamics was not at all clear, although the existence of something like what we now call the tachocline could be inferred from theoretical arguments.) Dicke and Goldenberg (1967b) reported finding a solar oblateness value of 5 × 10−5, which would be sufficient to create an 8% discrepancy between observations and the Einsteinian prediction for the precession of the perihelion of Mercury, and would imply a fast-rotating core.
The results, and the inferences Dicke and collaborators drew from them, raised a storm of controversy that may well have helped to stimulate interest in the Sun’s interior rotation profile. The criticisms and Dicke’s responses to them would fill a lengthy review article by themselves; we give only a few examples here. Roxburgh (1967) suggested that the result might be explained by the solar differential rotation, an idea rejected by Dicke and Goldenberg (1967a). Howard et al. (1967) concluded, on the basis of a variety of simple models of the solar “spin-down,” that the Sun should have reached a state of uniform rotation quite quickly after its initial formation. Sturrock and Gilvarry (1967) pointed out that the presence of magnetic field in the solar interior might well complicate the issue, and in an accompanying article Gilvarry and Sturrock (1967) suggested using a space probe in a highly eccentric orbit as a more direct test of general relativity — or, alternatively, that “more complete theoretical and observational knowledge of the visible layers and the interior of the Sun” was needed.
At least partly inspired by the controversy, Kraft (1967) studied the rotational velocities of young solar-type stars in the Pleiades and concluded that angular momentum was lost on a timescale of about half a billion years, but noted in his conclusion that “it is wrong to conclude that the present work in any way supports the Dicke result.” Goldreich and Schubert (1968) considered the stability of differentially rotating stars and concluded that it was possible but not likely that a radial rotation gradient such as that required by the Dicke and Goldenberg (1967b) result might exist.
H. Hill, a former colleague of Dicke who had helped to build the instrument with which the 1964 observations were made (Dicke, 1964), and collaborators, also attempted to measure the solar oblateness, using an instrument, SCLERA [Santa Catalina Observatory for Experimental Relativity by Astrometry], which was later to play a role in the early days of helioseismology. This measurement, carried out in 1973, (Hill and Stebbins, 1975), found a 9.6 × 10−6 value for the oblateness, much smaller than that of Dicke and Goldenberg (1967b). Hill et al. (1974) also pointed out a time-varying difference between the brightness of the solar limb and poles that might account for the anomalously high oblateness measurement.
Ulrich and Hawkins (1981a, b) made an early attempt to deduce what the J2 and J4 terms should be based on a simple differential rotation profile deduced from surface measurements, obtaining predicted values of between 1 and 1.5 × 10−7 for J2 and between 2 and 5 × 10−9 for J4 depending on the size of the convective envelope.
Dicke et al. (1986, 1987) repeated the 1966 measurements with an improved instrument, and obtained significantly smaller values for the oblateness, with some weak evidence for a solar-cycle variation. Lydon and Sofia (1996) made measurements using a balloon-based instrument and obtained values of 1.8 × 10−7 for J2 and 9.8 × 10−7 for J4. By this point, however, the focus in the solar oblateness studies had moved away from trying to infer the core rotation. Mecheri et al. (2004) used more realistic models of the internal rotation profile to suggest that the J4 term should be particularly sensitive to the subsurface shear. Recent work on determining the oblateness from the shape of the solar limb has taken into account considerations of near-surface temperature or magnetic variations. Kuhn et al. (1998) and Emilio et al. (2007) used observations from MDI during rolls of the SOHO spacecraft and Fivian et al. (2008) used the RHESSI X-ray telescope. The work with SOHO revealed a temporal variation in the shape of the solar limb, with greater apparent oblateness at solar maximum, suggesting that hotter, brighter activity belts have greater apparent diameter. This poses an apparent contradiction to the results obtained from helioseismic inferences of the asphericity. Indeed, Fivian et al. (2008) suggest that all the temporally-varying, excess oblateness found in the observations can be corrected away by removing an ad-hoc term related to magnetic elements in the enhanced network.
Meanwhile, a much more flexible tool — helioseismology — had become available for probing the interior solar rotation.
5.2 Early low-degree helioseismic results
Around the early 1970s there were numerous attempts to search for global p-mode oscillations, with interest at first focusing on longer-period oscillations, the low-order, low-degree modes. Various theoretical predictions (Scuflaire et al., 1975; Iben Jr, 1976; Christensen-Dalsgaard and Gough, 1976) of the periods were available, offering the hope that global oscillations could be used to probe the rotation and structure deep inside the Sun. At first most of the results (Livingston et al., 1977; Musman and Nye, 1977; Grec and Fossat, 1977), were negative, except for the 160-minute period of Severnyi et al. (1976); Brookes et al. (1976), which was later (Elsworth et al., 1989) determined to be spurious and will not be further discussed here. The SCLERA group (Brown et al., 1978; Hill and Caudell, 1979; Caudell and Hill, 1980) found a variety of longer-period fluctuations in their solar-diameter data, but these results were not universally accepted; for example Fossat et al. (1981a, see also references therein) claimed that the SCLERA results were consistent with pure noise.
Low-degree helioseismology became a reality when the Birmingham group (Claverie et al., 1979) identified oscillations in the five-minute frequency band in integrated sunlight as low-degree global modes, using observations from Tenerife and Pic du Midi during the summers of 1976–1978; these initial data were adequate only to identify the spacing between modes of the same l and different n, without resolving separate l = 0 and l = 1 peaks.
A French-American team (Grec et al., 1980; Fossat et al., 1981b) obtained five days of continuous observations at the South Pole in the austral summer of 1979–1980, and were able to identify peaks of degree 0, 1, 2, and 3 and even a weak l = 4 peak by superposing sections of the acoustic spectrum with different radial order. These modes were identified as being of radial order around 12–30, as opposed to the very low-order modes that had been sought in the low-frequency spectrum; both the noise characteristics of the spectrum and the low amplitude of the lower-order modes mean that the fundamental (l = 0, n = 1) mode remains unobserved to this day, although some low-degree modes with single-digit n have been identified (Chaplin et al., 1996b).
Soon, the Birmingham team (Claverie et al., 1981), using 28 days of integrated-sunlight data from the Tenerife site and an analysis that involved “collapsing” segments of the acoustic spectrum so as to average together modes of the same degree and different radial order, reported finding three rotationally split components in the l = 1 modes and five in l = 2, with an average separation of 0.75 µHz. If correct, this would have implied a solar core rotation substantially faster than the surface. Isaak (1982) suggested that the excess component peaks (when two and three would be the expected number for l = 1 and l = 2 respectively) could be explained if the solar core were rotating on an oblique axis and had a very strong magnetic field; this idea, which was also mooted by Dicke (1983) to explain an oscillation of about half the solar rotation period seen in the oblateness data (Dicke, 1976), was rebutted in some detail by Gough (1982).
Fossat et al. (1981b) reported that initial results from 5 days of low-degree observations at the South Pole suggested quite short lifetimes, about 2 days; the l = 0 peaks appeared narrower than those of l = 1 and l = 2. Grec et al. (1983) later identified about 80 normal modes in the South Pole data, but did not confirm the Claverie et al. (1981) rotational splitting result, instead reporting that the l = 1 peak seemed too narrow to accommodate the reported splitting.
Claverie et al. (1982) reported a periodicity of approximately 13 days in the radial solar velocity, as measured using the resonant-scattering technique and the potassium D-line, and interpreted this as an effect of the solar core rotation; however, this effect was quickly explained away (Durrant and Schröter, 1983; Andersen and Maltby, 1983; Edmunds and Gough, 1983; Duvall Jr et al., 1983) as an artifact caused by the rotation of surface features — sunspots and plage — across the disk.
Meanwhile, the low-degree five-minute acoustic spectrum had also been observed using the Active Cavity Irradiance Monitor (ACRIM) aboard the Solar Maximum Mission (SMM) spacecraft (Woodard and Hudson, 1983b). Woodard and Hudson (1983a) agreed with Fossat et al. (1981b) in finding that the modes had lifetimes of about two days, too short for the rotational splitting reported by Claverie et al. (1981) to be real.
Later work (Libbrecht, 1988a; Elsworth et al., 1990b; Chaplin et al., 1997) revealed that the width of the peaks — inversely proportional to the mode lifetimes — was strongly dependent on frequency across the five-minute spectrum, with lifetimes of a few days in the middle of the five-minute band and weeks or months at low frequencies where, unfortunately, the amplitudes of the modes are also small. Reliable direct measurement of the low-degree splittings would have to wait for some years, while sufficiently long, high-quality time series of data accumulated.
5.3 Resolved-Sun measurements
In the meantime, resolved-Sun observations provided some information about the rotation in the radiative interior. Duvall Jr and Harvey (1984) reported observations at Kitt Peak, from 10–26 May 1983, for degrees 0 ≤ l ≤ 100. When plotted as a function of degree, the results show a slow decrease in the rotational splitting, from the highest degrees down to about l = 6, with an unexplained bump at l = 11, followed by an increase at lower degrees up to a value of 660 nHz for l = 1. These data, inverted by Duvall Jr et al. (1984), yielded a rotation profile with much of the radiative interior rotating at or below the surface rate, but with a modest increase in the interior. A similar pattern was found by Brown (1985), using 6 days of observations from the newly-developed Fourier Tachometer, a true 2-dimensional imaging instrument that gave access to all the azimuthal orders for degrees between 8 and 50; however, the coincidence of the l = 11 bump seems to have been merely a coincidence of noise, as it was not reproduced in the early observations from the Big Bear Solar Observatory (Libbrecht, 1986).
5.4 The SCLERA modes
Hill et al. (1982) derived splittings from the SCLERA low-frequency peaks, and from those inferred a core rotating at 6 times the surface rate; however, Woodard (1984) used ACRIM data to place an upper limit of 2.2 times the surface rate on the interior rotation rate, inconsistent with these splittings. Later, Hill (1985) identified low-degree rotational splittings in the five-minute band of the SCLERA acoustic spectrum, but Libbrecht (1986) and Brown et al. (1989) found that these results were inconsistent with the other evidence and were probably the result of misidentification of the modes. Given the complexity of the spectrum in question, whose derivation from measurements sampled at a few points on the solar limb made it difficult to separate out spectra of different degree, this seems a likely explanation.
5.5 Low-degree acoustic mode splittings 1988–2002
The next several years were active ones for low-degree helioseismology, with the development of the BiSON (Birmingham-based) and IRIS (based in Nice) networks. Together with the IPHIR instrument that rode the PHOBOS spacecraft on its cruise phase to Mars, and the ground tests of the LOI (Luminosity Oscillations Imager) instrument that would later be mounted on the SOHO spacecraft, these brought a succession of estimates of the low-degree splitting, as summarized in Table 1 and Figure 14. In addition to the MDI instrument for medium and high-degree observations, the SOHO spacecraft carried both LOI and GOLF (Global Oscillations at Low Frequencies) specifically for observing low-degree modes. Even though GOLF malfunctioned and could not be operated in its intended differential mode, instead being confined to making Doppler observations on one side of an absorption line, it provided some of the best available long-term, low-degree observations.
The reported results show considerable variation, but apart from the early Tenerife result, which was based on much shorter and lower-duty-cycle observations than most of the others, they all cluster around the surface rotation rate, some (particularly the IRIS results) pointing to a core rotation faster than the surface rate and some (in particular the BiSON results) to one substantially below it, perhaps as low as zero. As we approach the present time and the observation and analysis improve, the values tend to converge on a splitting quite close to that which would correspond to the surface rate. Early in this period, there was room to speculate (e.g., Chaplin et al., 1996a) that the differences reflected a temporal variation, but this could not explain away all the discrepancies.
5.6 Pitfalls of low-degree splitting measurements
Unfortunately, all the measurements described in Section 5.5 suffer from similar problems, as summarized below:
-
1.
The two components of the l = 1 mode are so close together (probably less than one microhertz apart) that they are resolved only for modes below about 2.2 mHz. This has implications for the measurements:
-
(a)
Estimates of the splittings of unresolved components are highly prone to systematic error (Appourchaux et al., 2000a).
-
(b)
The components that can be resolved have small amplitudes (Figure 15) and therefore require both observations over extended periods and high signal-to-noise ratios.
-
(c)
On the other hand, these low-frequency modes have the advantage that they show very little frequency shift with the solar cycle, which simplifies the analysis of long time series.
-
(a)
-
2.
Even though the low-degree modes penetrate deep into the solar interior, they spend most of their time in the outer layers of the Sun and are not very sensitive to the core; conversely, estimates of the core rotation are very sensitive to small errors in the splitting measurements.
-
3.
In order to properly estimate the rotation profile in the deep interior it is necessary to combine the low-degree splittings with medium-degree ones in an inversion. However, because the low-degree modes are so few — a few dozen at most, compared to a couple of thousand medium-degree multiplets with tens of thousands of individual frequencies or coefficients — the need for extremely precise measurements is even more pressing. Also, combining data from different instruments with different systematic errors may cause problems, particularly if the observations were made at different epochs of the solar cycle.
Point 1 above was noted by Loudagh et al. (1993) and Elsworth et al. (1995), and point 2 by Loudagh et al. (1993) and Lazrek et al. (1996), who point out that “An accuracy of about 30 nHz, or (1 year)−1 on the measurement of the l = 1 rotation splitting does not really permit, then, to discriminate between a solar core rotating twice as fast as the rest or not rotating at all!”. An approach to addressing point 3 was made by Tomczyk et al. (1995) with the newly-built LOWL instrument, an imaging instrument optimized for lower degrees. They obtained splittings for 1 ≤ l ≤ 100, and inferred a rotational profile down to 0.2 R⊙, finding a rotation rate that barely varied with radius between 0.2 R⊙ and 0.6 R⊙, apart from a low-significance bump around 0.4 R⊙.
Eff-Darwich and Korzennik (1998) further addressed point 3 when they combined results from several different instruments, including GONG, BiSON, MDI, and GOLF. They give a nice illustration of the tendency of higher-frequency low-degree mode splittings to be biased upward by the mode width, a point that was further illustrated by Chaplin et al. (2001), and conclude that with the then-available data it is not possible to rule out fast rotation in the core below 0.18R⊙.
Charbonneau et al. (1998) used a genetic forward-modeling approach to analyze the LOWL data, with results favoring a rigidly-rotating core.
5.7 A new millennium for low-degree helioseismology
Starting around the turn of the century, there was a move towards more collaborations and comparisons between different projects in an effort to understand the systematic errors and better constrain the solar core dynamics. By this time, multi-year observations were available from GONG and the SOHO instruments, as well as good-quality observations from BiSON stretching back to 1991.
Chaplin et al. (1999) combined the LOWL higher-degree splittings with the very precise low-frequency BiSON splittings for the lowest-degree modes, and concluded that the data were consistent either with rigid rotation or with a slight downturn in the rotation rate in the core (the latter being at best a 1-σ result); on the other hand, Corbard et al. (1998b) had used a very similar analysis of GOLF and MDI data to deduce a slight increase in the rotation rate below 0.25 R⊙, but García et al. (2003), also using MDI and GOLF data, obtained rather low splitting values from a 2243-day time series and tentatively concluded that they could rule out a high rotation rate in the core.
Eff-Darwich et al. (2002), following on from the work of Eff-Darwich and Korzennik (1998), again combined BiSON, GOLF, GONG and MDI data and found a very small downturn in rotation in the core, while Couvidat et al. (2003) found a flat rotation profile down to 0.2 R⊙ using combined GOLF, MDI and LOWL data.
Fletcher et al. (2003) investigated the problem of fitting the poorly-resolved higher-frequency low-degree mode splittings to integrated-sunlight observations such as those from BiSON. Using genetic fitting algorithms, they were able to reduce, though not eliminate, the bias towards higher splittings for these fits. They also found, in common with previous work, a strong anticorrelation between the estimated splitting value and its formal error, which would tend to cause overestimated splittings to be more heavily weighted in inversions.
García et al. (2004) considered two years of “sun-as-a-star” observations from early in the solar cycle, obtained from GOLF, GONG, MDI, VIRGO and BiSON, and were able to extract not only sectoral splittings but also a3 and a5 coefficients from the data, suggesting that it may be possible to infer differential rotation even in stars from which we will never have resolved data.
Chaplin et al. (2004) used artificial data to address the question the detectability of a rotation-rate gradient in the core. They concluded that, based on the best available data from ten years of observations, the difference between the rotation rate at 0.1 R⊙ and 0.35 R⊙ would be detectable only if it exceeded 110 nHz.
Chaplin et al. (2006) carried out an exhaustive “hare-and-hounds” exercise, in which one participant (the “hare” supplies the same set of artificial data to the others, the “hounds,” who then apply their various fitting methods without knowing the “true” answer, and compare the results. They obtained good agreement between the different techniques for l = 1, but systematic differences for the l > 1 splittings, which are attributed to different assumptions about the relative heights and spacing of the non-sectoral (∣m∣ < l) components.
5.8 Summary of the acoustic-mode results
To summarize, the best evidence we have so far seems to imply that the rotation rate between about 0.2 R⊙ and the base of the convection zone is most likely approximately constant with radius and spherically symmetric. It is not possible to rule out a different rotation rate for the inner core, but there is no evidence from p-mode observations to support such a difference. Between about 0.2 R⊙ and the base of the tachocline, no significant departure from rigid-body rotation has been found. As discussed by Eff-Darwich et al. (2002), for example the available constraints already seem to rule out the simplest models of hydrodynamic spin-down, which would show a detectable increase in the rotation rate below 0.3 R⊙. Understanding both of the relationship between p mode splittings and the interior rotation, and of the care needed to measure them, has greatly advanced since the early days of helioseismology, but the rotation rate of the innermost nuclear-burning core remains uncertain.
5.9 Gravity modes
One possible way to improve the constraints on the core rotation would be to use g modes, or gravity waves, instead of p modes. Because these modes have their greatest amplitude in the solar interior, they should be much more sensitive to the core properties. Unfortunately, they also have very small amplitudes at the surface. The history of helioseismology is littered with unconfirmed reports of g-mode identification; see, for example, Delache and Scherrer (1983), van der Raay (1988),Thomson et al. (1995), and the review by Hill et al. (1991b). The most promising recent work has been carried out using long time series from the GOLF instrument aboard SOHO. Appourchaux et al. (2000b) placed an upper limit of 10 mm/s on g-mode amplitudes based on two years of observations, and Gabriel et al. (2002) reduced this limit further, to 6 mm/s, using 5 years of data. Most recently, García et al. (2007) report finding a pattern of peaks with constant spacing in period corresponding to the model-predicted spacing for l = 2 g modes with δl = 0, δn = 1, and with a splitting that they interpret as corresponding to a core rotation rate of 3–5 times the surface rate; however, this is still a preliminary result in need of confirmation.
In a related paper, Mathur et al. (2007) point out that the current predictions for low-order g-mode frequencies are much more consistent than was the case a decade earlier, resulting in a period for the fundamental g-mode between 34–35 minutes. This finding does make one wonder about the usefulness of the g-mode observations for discriminating among models; on the other hand, it lends somewhat more credence to the current identification.
6 The Tachocline
6.1 Observations
While the bulk of radiative interior appears to rotate almost as a solid body, the base of the convection zone at 0.71 R⊙ coincides with a region of strong radial shear, above which the convection zone exhibits a differential rotation pattern that depends strongly on latitude and only weakly on depth. This shear layer is known as the tachocline, a term introduced to the literature by Spiegel and Zahn (1992), who attribute to D.O. Gough the correction of the earlier term “tachycline” (Spiegel, 1972). As is evident from the date of the latter reference, the notion of a shear layer at the bottom of the convection zone had been present in models for some time prior to its observational discovery, though its exact location was somewhat uncertain.
The existence of a layer of radial shear around the base of the convection zone, with approximately solid-body rotation below it, was first demonstrated by Brown et al. (1989), using the data of Brown and Morrow (1987); however, the significance of their results was quite low and they were at pains to point out that other interpretations of the data were possible. Dziembowski et al. (1989) used BBSO data to improve the picture of rotation at the base of the convection zone, again finding that the low-latitude rotation rate increased, and the high-latitude rate decreased, towards a common value at the base of the convection zone. The position of the base of the convection zone was determined by Christensen-Dalsgaard et al. (1991) using sound-speed inversions of helioseismic frequencies from the work of Duvall Jr et al. (1988) and Libbrecht and Kaufman (1988); their value of 0.713 R⊙, confirmed by Basu and Antia (1997), has been accepted ever since.
The discovery of this shear layer (as pointed out by Brown et al.) offered a solution to the puzzle of the apparent absence of a radial gradient of rotation in the convection zone that could drive a solar dynamo, leading to speculation that the dynamo must operate in the tachocline region instead of in the bulk of the convection zone.
The tachocline lies in the region where modes of l ≈ 20 have their lower turning points, and the resolution of the inversions is quite low — about 5–10% of the solar radius in the radial direction. The thickness of the shear layer is therefore likely not to be resolved in inversions, and some ingenuity (and forward modeling) is required to estimate it and account for the effect of the finite-width averaging kernels in smoothing out the inversion inferences. The results of various efforts to parameterize the tachocline shape at the equator are summarized in Table 2. They mostly concur in placing the centroid of the shear layer slightly below the seismically-determined base of the convection zone, and its thickness at around 0.05 R⊙. The largest value for the thickness, that of Wilson et al. (1996b), was obtained using forward calculation and direct combination of splitting coefficients rather than a true inversion, while the very low value of Corbard et al. (1999) was obtained using an inversion technique specifically designed to allow a discontinuous step in the rotation rate at the tachocline. The analysis of Elliott and Gough (1999) was somewhat different from the others, in that it involved calibrating a particular model of the tachocline against the inferred sound-speed rather than against a rotation profile.
Antia et al. (1998) and Corbard et al. (1999) found no significant evidence for a variation in the position or thickness of the tachocline with latitude, but Charbonneau et al. (1999) found a significant prolateness, with the tachocline (0.024 ± 0.004) R⊙ shallower at latitude 60° than at the equator. Basu and Antia (2003) also found a slightly thicker and shallower tachocline at high latitudes, and speculated that the tachocline location might be discontinuous at the latitude (around 30°) where the shear vanishes and changes sign.
6.2 Models and the tachocline
Even the most generous estimates for the observed tachocline thickness are small enough to pose an interesting theoretical question: what prevents the shear from spreading further into the radiative interior, destroying the observed uniform rotation? The literature on tachocline modeling is extensive, far beyond the scope of this review. In brief, three main candidate mechanisms have been proposed: turbulent flows (Spiegel and Zahn, 1992); “fossil” magnetic fields (e.g., Gough and McIntyre 1998); and gravity waves, known to observational helioseismologists as g modes (e.g., Zahn et al. 1997), but all these scenarios have problems when considered as the sole mechanism. Recent advances in computing have made possible detailed three-dimensional simulations to explore these issues, but these models have not yet been able to reproduce a self-sustaining tachocline. For a review from a modeler’s perspective, see Miesch (2005). Also, a variety of discussions of tachocline models are collected in the book edited by Hughes et al. (2007).
7 Rotation in the Bulk of the Convection Zone
7.1 Observational history
The surface differential rotation, with the equator rotating faster than the poles, was known from, for example, sunspot tracking, long before helioseismology opened up the solar interior. Most models in the pre-helioseismology era predicted or assumed a rotation rate constant on cylinders parallel to the axis of rotation. This is a consequence of the so-called Taylor-Proudman constraint, a well-known result in fluid dynamics.
Duvall Jr and Harvey (1984) and Duvall Jr et al. (1984) observed from the South Pole, using only sectoral modes; their instrument used intensity images in a Calcium absorption line, scanning rather than imaging the whole Sun at once. Their main conclusion was that: “Most of the Sun’s volume rotates at a rate close to that of the surface”.
Brown (1985) had a different instrument, the Fourier Tachometer, which produced 100 × 100 pixel velocity images. Brown’s initial crude analysis of five days of data used cross-correlation, and expanded the multiplet frequencies using low-order polynomial fits; the results showed little sign of any depth variation in the differential rotation.
Duvall Jr et al. (1986), again using data from South Pole observations but now covering the full range of azimuthal orders, found values of the a3 coefficient (the first-order measure of differential rotation) consistent with the surface rotation and rather larger than was consistent with the results of Brown (1985).
Brown and Morrow (1987), with 15 days (not all consecutive) of Fourier Tachometer data, could not distinguish between rotation on cylinders and latitude-dependence, but found that there was definitely less differential rotation in the radiative interior below the convection zone; their a3 values were now closer to those of Duvall Jr et al. (1986), and they declared the previous ones erroneous. Brown et al. (1989) carried out a much more detailed analysis of the Brown and Morrow (1987) data, strengthening the evidence for mostly depth-independent rotation in the convection zone, as shown in Figure 16.
Summary of rotation inferences from Brown et al. (1989) (reproduced by permission of the AAS).
Both the South Pole observations and those of Brown and collaborators were relatively noisy and of poor resolution; although they strongly hinted at a picture with little radial differential rotation in the convection zone and little differential rotation at all below it, other interpretations were possible.
Libbrecht (1989) published splittings from 100 days of BBSO observations in summer 1986, broadly confirming the results of Brown et al. (1989) with substantially smaller uncertainties. Dziembowski et al. (1989) inverted these data, and inferred a sharp radial gradient at the base of the convection zone and roughly constant rotation at each latitude above that. They also found a bump in the rotation rate in the middle of the convection zone, to which we will return below. Other inversions of the same data set were presented by Christensen-Dalsgaard and Schou (1988) and Libbrecht (1988b), with similar results, though not all the early inversions (cf. Korzennik et al. 1988; Sekii 1991) produce such recognizable results; this may be an example of the difficulty of using OLA-type techniques for data with insufficient higher-degree modes. Another (2dOLA) inversion of these data, shown in Figure 17, was carried out by Schou et al. (1992), who illustrated their averaging kernels; these were rather broad, but adequate to rule out a rotation-on-cylinders model. This paper was also the first to make the important point that the so-called “polar” rotation rate inferred from inversions is actually localized somewhat away from the pole.
Rotation profile based on analysis of BBSO splittings, (Schou et al., 1992) (reproduced by permission of the AAS).
Gough et al. (1993) continued to challenge the observers to completely exclude rotation on cylinders, pointing out that it was possible to construct a cylindrical model that satisfied the constraint of the BBSO data, but Schou and Brown (1994b) showed that such a model could not be made consistent with both the Fourier Tachometer data and the gravitational stability of the rotating Sun.
Bachmann et al. (1993) analyzed Fourier Tachometer observations from 1989 and pointed out a “wiggle” in the splitting coefficients at ν/L ≃ 40µHz, (corresponding to a turning-point radius of about 0.85 R⊙); attributed to daily modulation of the observations, this now well-known effect accounts for the “feature” seen in the middle of the convection zone in many inversions of single-site data.
Better data, with long time series free from daily modulation, were obviously needed before much more progress could be made, and with the advent of the GONG network in 1995 and the MDI instrument aboard SOHO in 1996 such data became available. Preliminary rotation profiles were presented by Thompson et al. (1996) for GONG and by Kosovichev et al. (1997) for MDI, both showing the now familiar pattern of almost-constant rotation in the convection zone, with shear layers both at the base of the convection zone and below the surface.
Schou et al. (1998) carried out a comprehensive analysis of the rotation profile based on the first 144 days of observations from MDI, using and comparing several different rotation inversion techniques with an input data set consisting of coefficients up to a36 for p modes up to l = 194 and f modes up to l = 250. They were able to obtain consistent and robust results from the surface to about 0.5 R⊙ at low latitudes; at higher latitudes the domain of reliability was shallower. Roughly speaking, the inversions could not be well localized within about 0.2 R⊙ of the rotation axis. The results (Figure 18) showed that the rotation in the bulk of the convection zone, below 0.95 R⊙, had a slow increase with radius at most latitudes, but was definitely incompatible with rotation on cylinders.
7.2 The “polar jet”
In addition to the other general features described here, Schou et al. found some evidence for a “jet” of faster rotation at about 75° latitude and 0.95 R⊙; although this was more obvious in some inversions than in others, it did seem to have a signature in the coefficients themselves (see also Howe et al. 1998). However, this feature was not reproduced in inversions of GONG data (e.g., Howe et al., 2000b), or even in inversions of MDI data analyzed with the GONG pipeline (Schou et al., 2002), and it is now believed to be an artifact related to the MDI data analysis.
7.3 GONG/MDI comparison
Once both GONG and MDI had been running for a few years, it became evident that the two projects were producing inferences of the interior rotation profile that were different in some significant details, particularly at high latitudes within the convection zone. Schou et al. (2002) carried out a careful comparison, taking data from three epochs at different phases of the solar cycle from each project and deriving rotational splittings or splitting coefficients from each, both with the usual algorithms and with those regularly used for the other project’s data, before using both RLS and OLA inversions. The results clearly showed that most of the discrepancies arose from the analysis pipelines rather from the data themselves. The “CA” peak-fitting algorithm used for the MDI data was able to extract modes from the GONG data to somewhat higher degrees and lower frequencies than the “AZ” algorithm could manage with either GONG or MDI input data. However, for both MDI and GONG data, the “CA” algorithm introduced an anomaly in the splitting coefficients centered at around 3.3 mHz, which in turn caused the inversion inferences to show a higher rotation rate deep in the convection zone at higher latitudes. Excluding these data brought the GONG and MDI data (analyzed with the “AZ” and “CA” pipelines respectively) into much better agreement, at the cost of somewhat degraded resolution. Restricting both data sets to the common mode set below 3 mHz reduced the discrepancies even farther, but did not remove the “jet” in the MDI data. Since the “jet” feature was only seen in the MDI data analyzed with the CA pipeline, however, the authors concluded that this feature was probably spurious.
7.4 Slanted contours
Although much of the debate in the early 1990s centered on discriminating between rotation constant on cylinders and rotation constant along radial lines, neither picture gave a complete description of the data. Gilman and Howe (2003) and Howe et al. (2005) pointed out that the differential rotation in the bulk of the convection zone, at least at low- to mid-latitudes, could be quite well described by saying that the contours of constant rotation lay at about a 25° angle to the rotation axis, as illustrated in Figure 19.
Figure 20 compares idealized rotation profiles for the cylindrical, radial, and slanted-contour configurations.
Idealized rotation profiles for rotation constant on cylinders (left), radial lines (middle), and lines at 25° to the rotation axis (right). The top row shows contours of constant rotation, while the lower row shows rotation rate as a function of radius at constant latitude for latitudes at 15° intervals from the equator (top) to 75° (bottom). The rotation rate is matched to the GONG inferences at 0.99 R⊙ and smoothed to simulate the broadening effect of inversion resolution on the tachocline; the near-surface shear was not included.
7.5 Polar rotation
Another interesting feature revealed by the early GONG and MDI observations (Schou et al., 1998; Birch and Kosovichev, 1998) was that, while the surface rotation rate was mostly well described by the usual three-term expansion in the cosine of the colatitude θ, Ω(θ) = A + B cos2 θ + C cos4 θ, (e.g., Snodgrass 1984) the rotation rate close to the poles was significantly slower than that. The authors speculated that this might be a result of drag from the solar wind, and that the effect might therefore disappear or become less marked at epochs of higher activity. In fact, though the inferred high-latitude rate did speed up during solar maximum — as seen, for example, in Howe et al. (2005) and in Figure 26 — it remained at all times lower than the extrapolation of the three-term fit.
7.6 Models and rotation in the convection zone
The interior rotation is only one part of the complex system that drives the solar cycle, but it is perhaps still the easiest part to measure in the solar interior; the meridional circulation can be directly measured only in the shallower subsurface layers, and buried magnetic fields can at best only be inferred indirectly. The differential rotation in the convection zone must arise from the interaction of convection cells and Coriolis forces, with the meridional motions playing an important part.
Early depictions of the solar dynamo (see, for example, Köhler 1974; Durney 1975) required a rotation rate increasing inward, and a meridional flow rising at the poles and sinking at the equator, in order to drive the solar cycle migration of the activity belts in the observed sense. This picture, taken together with rotation on cylinders, would have meant that the observed surface differential rotation was a superficial phenomenon, with the dynamo operating in the unobservable deeper layers. At this stage, there does not seem to have been a clear distinction made between the direction of the meridional circulation at the surface and the direction of migration of the magnetic activity belts during the solar cycle, which are of course now understood to operate in opposite directions; the poleward meridional flow at the surface was first measured by Duvall Jr (1979).
The models of Glatzmaier (1985) and Gilman and Miller (1986), which were among the first numerical simulations of solar rotation and the dynamo, have been cited, for example by Wilson (1992) as dating from “Prior to the advent of helioseismology,” but this is not quite correct. In fact, both these papers refer to the Duvall and Harvey data, and Gilman and Miller (1986) also mentions the observations of Brown (1985), suggesting that the model results could be consistent with the helioseismic observations if there were a layer of inward-increasing velocity below the surface and above the domain of the simulation. The simulations in both cases, like their precursors over the previous several years such as that described by Gilman and Miller (1981), produced rotation approximately constant on cylinders and increasing outward, which would result in a dynamo wave propagating poleward if the dynamo were operating in the bulk of the convection zone. The main message that modelers in the late 1980s seem to have taken from the observations was that the rotation rate was increasing outward, in agreement with the simulations of Gilman and Miller (1986) but in disagreement with the α-effect dynamo picture, which required a rotation rate increasing inward; see Parker (1987) for a review representing a theorist’s perspective on the state of play at this stage. This led Gilman and Miller (1986) to suggest (not for the first time; see also, for example, Galloway and Weiss 1981) that the dynamo might be operating in a thin layer at the bottom of the convection zone; this speculation was further reinforced by the later helioseismic inferences that clearly showed this shear layer, or tachocline (see Section 6) and the approximately radial configuration of the rotation in the convection zone.
Even quite recent global simulations of convection (Brun et al., 2004, for example,) still show some tendency towards rotation on cylinders, but the higher-resolution calculation of Miesch et al. (2008) mostly eliminates the cylindrical effect and produces a rotation pattern, based on giant convection cells, that after suitable temporal averaging looks quite solar-like, as illustrated in Figure 21.
8 The Near-Surface Shear
One persistent puzzle in the measurements of rotation at the photosphere had been that direct Doppler measurements consistently gave somewhat slower rotation rates than the measurements made by tracing surface features. For example, Brown et al. (1989) summarized the results of Snodgrass (1983, 1984) as
for magnetic features and
for the surface plasma, respectively, where μ is the sine of the latitude. For an overview of such measurements, see Beck (2000). The usual explanation for the discrepancy is that while the Doppler techniques measure the velocity at the surface, the tracers such as sunspots are anchored in a faster-rotating layer deeper down. For example, Gilman and Foukal () noted that the observations implied a subsurface shear layer and suggested that this might arise from angular momentum conservation in the supergranular layer.
An extremely early attempt to measure the subsurface rotation was made by Rhodes Jr et al. (1979), when the identification of the 5-minute oscillations with p modes was still a relatively recent discovery. These authors used high-degree modes, probing about the upper 20 Mm (0.03 R⊙) of the convection zone, and detected an inwards-increasing gradient. If these measurements are reliable, they represent the first detection of the subsurface shear. However, most of the early helioseismic measurements of the internal rotation profile were restricted to a degree range that did not allow the near-surface shear to be resolved in inversions. Rhodes Jr et al. (1990), attempting to measure the rotation in the bulk of the convection zone, also saw hints of a gradient, opposite to that seen at the base of the convection zone, below the surface, and Wilson (1992) used forward calculation techniques on the data of Brown and Morrow (1987) and Libbrecht (1989) to deduce that the rotation rate must increase inward immediately below the surface. We should remember, however, that at this time the picture of the internal rotation profile was not as clear as it is today, and it is not always obvious whether interpretation of the observations as gradients of rotation refers to the near-surface shear, the shear at the base of the convection zone, or some unresolved amalgamation of the two. Wilson, for example, was not arguing for a near-surface shear layer but against the model with rotation constant along radii.
With the advent of GONG and MDI, measuring modes to higher degrees than had previously been possible, the near-surface shear could be seen in global inversions; it is visible in the early results presented by Thompson et al. (1996) for GONG and by Kosovichev et al. (1997) for MDI, in both cases apparently changing sign at higher latitudes.
Schou et al. (1998) found clear evidence of the near-surface shear in inversions of MDI data. All the inversion methods agreed well on the shear at low latitudes, but at high latitudes the picture was complicated by the proximity of the submerged “jet” feature and the methods agreed less well. The disagreement may have been partly due to systematic errors in the splitting coefficients. In the comparisons of MDI and GONG data and analysis carried out by Schou et al. (2002), the high-latitude reversal of the shear is seen only in data analyzed with the “CA” pipeline; this may be partly because the “AZ” pipeline mostly fails to recover the splittings of the (narrow, low-amplitude) f-mode peaks, but the reversal persists in the MDI data even for the restricted common mode set.
The near-surface shear (down to about 15 Mm) was studied in detail by Corbard and Thompson (2002), using f modes from MDI data. They measured the slope of the rotation rate, close to the surface at low latitudes, as about −400 nHz/R⊙, decreasing to a very small value by about 30° latitude and possibly reversing in sign at higher latitudes (though this result, seen in only the outer 5 Mm, was dependent on only the highest-degree modes, those with l ≥ 250). The low-latitude rotation rate was found to vary almost linearly with depth in the subsurface region, while if angular momentum was conserved in parcels of fluid moving with respect to the rotation axis, it would be expected to vary with the inverse square of the distance from the axis.
The near-surface shear is also accessible to the methods of local helioseismology, at least for latitudes below 50–60°. Basu et al. (1999) and Howe et al. (2006a) compared results from local ring-diagram analysis and global inversions and found, at latitudes ≤ 30°, quite good agreement between the dΩ/dr values obtained from local and global inversion results. However, although the slope from local measurements does show some variation with latitude (Figure 22), it by no means vanishes at 52.5°, the highest latitude at which the measurement is made. The ring-diagram results allow us to consider the northern and southern hemispheres separately, but Basu et al. (1999) found very little difference in the shear between the two hemispheres.
Radial variation of the mean rotation rate after subtraction of the tracking rate, for global inversions (blue) and north-south averaged local inversions of MDI (green) and GONG (red) data at latitudes 0° (a), 15° (b), 30° (c), and 45° (d); similar to Howe et al. (2006a).
Some attempts have been made to use the near-surface shear to drive or at least contribute to a solar dynamo, for example by Brandenburg (2005), but Dikpati et al. (2002) showed that any dynamo contribution from the shear of the outer layers could only provide a fraction of the effect needed to power the solar cycle.
9 The Torsional Oscillation
9.1 The torsional oscillation before helioseismology
The so-called Torsional Oscillation is a pattern of migrating bands of faster- and slower-than-average zonal (i.e., parallel to the equator) flow associated with the equatorward drift of the activity belts during the solar cycle. It was first described by Howard and LaBonte (1980), who used 12 years (1966–1978) of full-disk velocity observations from the 150-foot tower at the Mount Wilson observatory and found evidence of a pattern of flow bands migrating towards the equator; the greatest concentration of active regions is associated with the poleward edge of the main equatorward-moving band. They initially interpreted the high-latitude variations as consisting of bands of faster rotation starting at the poles and taking a full 22-year Hale cycle to drift to the equator. Scherrer and Wilcox (1980a) and Scherrer et al. (1980), observing at the Stanford Solar Observatory, found no evidence of changes in the equatorial rotation rate for data from 1976–1979, but as this period was close to a solar minimum, and the resolution of the Stanford instrument was not high, this is neither surprising nor inconsistent with the results of Howard and LaBonte. LaBonte and Howard (1982) note that Scherrer and Wilcox (1980b) (at a AAS meeting), had “confirmed the existence of the global velocity field,” though this is not apparent from the latter’s published abstract.
A somewhat different pattern of velocity variations is seen when magnetic features rather than Doppler measurements are used to determine the surface rotation rate, as described for example by Komm et al. (1993a), who found that the pattern derived from magnetograms lay equatorward of that from Doppler measurements, with the slower-than-average bands coinciding with the zones of greater magnetic flux.
Mount Wilson Doppler observations since 1986, clearly showing the pattern of migrating zonal-flow bands, were presented by Ulrich (1998, 2001); see also Howe et al. (2006a) for updated results. The bands extend over about 10° in latitude, and have zonal velocities a few meters per second faster or slower than the surrounding material, corresponding to excess angular velocity of less than 0.5% of the overall rotation, or a few nanohertz.
9.2 Early helioseismic measurements
The first hints of the signature of the migrating flow bands in helioseismic data can be seen in the BBSO data (Woodard and Libbrecht, 1993), as was pointed out by Howe et al. (2000c), but these measurements do not give much information on the radial extent of the flows. Kosovichev and Schou (1997) found evidence of the flows, a few meters per second faster than the general rotation profile, in f-mode measurements from early MDI data; Giles et al. (1998) found a similar pattern using the time-distance technique of local helioseismology, while Schou (1998) and Schou (1999) clearly showed that these flows were migrating in a manner consistent with the Mount Wilson Doppler observations. The first radially-resolved evidence of zonal flow migration was reported by Howe et al. (2000c) for GONG and by Toomre et al. (2000) for MDI, while Howe et al. (2000a) combined MDI and GONG data and concluded that the equatorward-migrating part of the flow pattern (at latitudes below about 40°) penetrated to at least 0.92 R⊙ (56 Mm below the surface). Antia and Basu (2000) also reported similar findings. Antia and Basu (2001) studied the evolution of the variations poleward of 50°, which had much higher amplitudes than the equatorward-moving flows and which showed signs of propagating poleward over time. The larger amplitude of the high-latitude signal may be related to the smaller angular momentum closer to the rotation axis.
9.3 Recent results
As more data accumulated, the signature of the torsional oscillation pattern in the helioseismic observations became clearer. Vorontsov et al. (2002) studied the evolution of the flows in MDI data from 1996 through 2001. They concluded that at least the high-latitude region of changing rotation involves the whole depth of the convection zone. The results on the radial extent of the flows at lower latitudes were less clear, with evidence that the bands of slower rotation might penetrate close to the base of the convection zone, while the bands of faster rotation appeared to reach about 0.9 R⊙ but no deeper. Another interesting feature of that paper was the introduction of the use of 11-year sinusoids to characterize the variation of the rotation rate at any given location. This innovation had the useful effect of clarifying the pattern, making obvious the poleward propagation of the high-latitude flows even with data from little more than half a cycle. The existence of a weak third-harmonic component to the 11-year cycle, however, was not confirmed in later work.
Basu and Antia (2003) found similar results in MDI and GONG data up to 2002, as seen in Figure 23. These results also hint at another subtlety; at low latitudes, the phase of the flow pattern is not constant along radial lines. In fact, the variation in the lower part of the convection zone appears to lead that close to the surface by a year or two, with the low-latitude band of faster rotation following roughly the same 25° slant as the rotation contours. This tendency was further studied by Howe et al. (2005, 2006b), who compared inversions of MDI and GONG data with forward-modeled profiles based on different flow configurations, including some derived from dynamo models. Although some detail was lost and distorted due to the resolution and uncertainties in the inversions, the authors were able to conclude that the low-latitude branch probably penetrates through much of the convection zone, but is sufficiently displaced in phase at greater depths that the correlation between the surface pattern and that deeper down almost vanishes. In this work, the 11-year sinusoid analysis showed evidence of a second-harmonic component rather than the third harmonic reported by Vorontsov et al. (2002).
Contour diagrams of constant rotation velocity residuals at 0.98R⊙, obtained using two dimensional RLS inversion of the GONG data, from Basu and Antia (2003) (reproduced by permission of the AAS).
Zonal flow pattern derived from MDI f-mode measurements, with smooth profile subtracted. Based on a figure from Schou (1999), updated and used by kind permission of J. Schou (2008, private communication.)
Figures 25, 26, and 27 show the variations in rotation rate, based on the results and figures in Howe et al. (2005, 2006b), but brought up to date with the most recent GONG and MDI observations available at the time of writing. The plots were prepared using the same 2dRLS inversion codes for both MDI and GONG medium-degree data, and 2dSOLA for MDI, that were used for the work of Howe et al. (2000a) and the other related papers. Figure 28 shows the phase and amplitude profiles for 11-year sine functions fitted to the rotation variations.
9.4 Local helioseismology and the torsional oscillation
The torsional oscillation pattern, at least at lower latitudes and closer to the surface, is also suitable for measurements using the techniques of local helioseismology, in which short-wavelength, short-lived waves are used to infer the structure and dynamics of localized areas of the Sun. Because these waves do not penetrate very far below the surface, such techniques are restricted to the outer few megameters of the solar envelope, but this region can be studied in much greater detail and with shorter averaging times than is possible with global helioseismology.
Basu and Antia (2000) detected the zonal flow migration using MDI data and the ring-diagram technique (Hill, 1988), in which the displacement of three-dimensional acoustic power spectra derived from small areas of the solar disk is used to infer horizontal flows in both the zonal and meridional directions. Later, Haber et al. (2002) measured both the zonal flows and a corresponding modulation of the meridional flow pattern, as seen in Figure 29 (left). Beck et al. (2002), using the time-distance technique, which considers the correlations between oscillations at spatially separated locations, also found bands of meridional flow away from the activity belts associated with the zonal flow bands. Chou and Dai (2001) and Chou and Ladenkov (2005), using data from the Taiwan Oscillations Network [TON]), also found diverging meridional flows associated with the activity belts. Zhao and Kosovichev (2004) measured the zonal (Figure 29 right) and meridional flows with the time-distance technique, and reported meridional flow converging on the activity belts above a depth of 12 Mm, with diverging flows below 18 Mm, forming circulation cells around the activity belts. The presence of inflows into the activity belts was also observed at the surface by Komm et al. (1993b) and Komm (1994). Komm et al. (2005) studied the flows in about a year of high-resolution GONG (“GONG+”) data, and concluded that the overall flow pattern existed whether or not active regions were included in the analysis; in other words, the zonal flow bands and their associated converging/diverging meridional flows appear to exist independently of the flows in the immediate vicinity of strong active regions.
Howe et al. (2006a) compared the results from ring-diagram analysis of the MDI data, global analysis of MDI and GONG data, and the Mount Wilson Doppler observations. They found very similar results for the north-south symmetrized flow pattern close to the surface in all three observations. Both the global and local helioseismic data indicated that the strength of the flow pattern did not fall off steeply below the surface.
It should be noted that the local helioseismic observations are somewhat prone to systematic errors, some of which follow the changing B0 angle, or tilt of the solar rotation axis relative to the observer, as shown for example by Zaatri et al. (2006). This can result, for example, in a pronounced and almost certainly non-solar north-south variation of the zonal flow measurements, which is generally corrected for by subtracting suitable averages.
Some further features of the torsional oscillation pattern as we know it from a full cycle of observations from GONG and MDI (and nearly two cycles of surface Doppler observations) are worth noting:
-
1.
The exact appearance of the pattern is quite sensitive to the background term that is subtracted. For example, compare the f-mode results shown in Figure 24, which were plotted as the difference from a smooth 3-term expansion of the rotation rate, with the plots in Figure 25, which were plotted by subtracting the temporal mean at each location.
-
2.
Although the pattern repeats — of course not precisely — with each (approximately) 11-year activity cycle, each equatorward-migrating flow band exists for about eighteen years, emerging at mid-latitudes soon after the maximum of one cycle and finally disappearing at the equator a couple of years after the minimum of the following cycle; thus, the band of faster rotation associated with the activity of cycle 22 was still visible at the beginning of GONG and MDI observations in early cycle 23, and the band that is expected to accompany cycle 24 became visible around 2002 (if we look at the mean-subtracted residuals), or 2005–2006 (if we use the smooth-function subtraction). On the other hand, each poleward-moving branch seems to last only about nine years, appearing a year or so after solar minimum and moving to the pole before the next minimum.
-
3.
Although the equatorward-migrating bands of faster rotation are clearly associated with the migrating activity belts of the magnetic butterfly diagram, the relationship is not completely straightforward. The new equatorward-propagating branch is clearly visible some years before noticeable new cycle active regions begin to erupt, and the phase/latitude profiles of the magnetic index and the velocity are very different. Also, as was noted by LaBonte and Howard (1982) and by Howe et al. (2006a), the strength of the torsional oscillation signal has not shown much change over the last few solar cycles, while the level of magnetic activity varies much more from one cycle to another.
-
4.
Although the equatorward branch of the zonal flow migration pattern shows some relationship to the pattern of enhanced activity in the Fe xiv corona going back to 1973 (Altrock, 1997), the “extended solar cycle” seen in these observations starts at a much higher latitude, apparently about 70°, before migrating to the equator over about eighteen years; thus even the equatorward edge of these coronal activity bands seems to be at higher latitude than the observed new branch in the zonal flows that starts at about the same time.
-
5.
Finally, we note that because the angular velocity changes associated with the torsional oscillation signal are relatively small compared to the difference in angular velocity between the surface and the bottom of the near-surface shear layer, while the amplitude of the signal does not decrease rapidly with depth, the magnitude of the shear at a given location varies by only a fraction of its value during the solar cycle. However, the fractional change in the shear is much greater than the fractional change in the rotation rate.
9.5 Models of the torsional oscillation
While observers, for example Howard and LaBonte (1980) and Ulrich (2001), have speculated that the torsional oscillation pattern might itself be part of the driving mechanism for the solar cycle, perhaps generating activity by shearing magnetic loops, modelers have generally seen it rather as a side-effect of the magnetic fields.
Schüssler (1981) and Yoshimura (1981) modeled the torsional oscillation as a result of the Lorentz force due to dynamo waves; according to the latter paper, the phenomenon would be important only close to the surface, and would have only equatorward, not poleward, moving bands. LaBonte and Howard (1982) objected to the Yoshimura model on the grounds that it would predict a strong correlation between the strength of the surface magnetic field and that of the velocity signal, which did not seem to be the case in the observations.
Küker et al. (1996) used a different mechanism to generate the torsional oscillation signal in their model, considering it as the response of the Reynolds stress on the time-dependent dynamo magnetic field rather than a direct effect of the large-scale Lorentz force. This model gave a very weak poleward branch for the torsional oscillation signal.
Once the flows had been shown observationally to penetrate well below the surface, Durney (2000) suggested that, “the pattern of torsional oscillations appear to have the potential of critically discriminating between different dynamo models as, e.g., the Babcock-Leighton and interface models.”
Covas et al. (2000) used a model in which the observed rotation profile was imposed and the rotation variations arises from the action of the Lorentz force of the dynamo-generated magnetic field on the angular velocity. They were able to simulate approximately solar-like patterns of zonal flow bands and magnetic activity. In subsequent papers they focused on the the possibility of so-called “spatio-temporal fragmentation” allowing cycles of different periods in different regions, and in calculations with no density stratification in the convection zone they found this to be feasible (Covas et al., 2001a). The effect was not too sensitive to uncertainties in the rotation law (Covas et al., 2001b, 2002), and somewhat sensitive to the boundary conditions at the outer surface (Tavakol et al., 2002). Adding density stratification (Covas et al., 2004) did not substantially change the results, though the amplitude of the oscillations in the deeper layers of the convection zone did decrease as the density gradient increased. However, they did find that introducing quite a small amount of α-quenching (magnetic feedback on turbulent convection) would suppress the torsional oscillation effect.
Spruit (2003) modeled the torsional oscillation pattern as a “geostrophic flow” driven by temperature variations near the surface associated with magnetic activity, and therefore having its greatest amplitude at the surface and falling to 1/3 of its surface value at 0.92 R⊙. This model also accounts for the observed inflows into the activity belts. There are some problems in reconciling this model with the observations; it is difficult to see how the observed depth-dependent phase pattern could arise from a surface-originated cause, and the existence of the flows even at epochs where there are no active regions is also hard to explain, though Spruit suggested that the flows might be produced by unobserved small-scale and short-lived magnetic regions.
Rempel (2007) used a mean-field flux-transport dynamo model, with a model-derived differential rotation profile and meridional flow, to investigate the effects of various driving mechanisms for the torsional oscillation. The author concluded that the poleward-propagating branch of the pattern could be explained by a periodic forcing at mid-latitudes without any underlying migration of buried polar field. On the other hand, in this type of model the observed equatorward-propagating branch could not be reproduced without adding a thermal forcing after the manner of the Spruit (2003) model. Howe et al. (2006b) compared such a model with the observations, and found it not to be completely consistent with the observed interior behavior of the flows at lower latitudes.
10 Tachocline Variations
10.1 The 1.3 year signal
Howe et al. (2000b) reported finding variations of the equatorial rotation rate close to the tachocline with a 1.3 year period during the early years (1995–1999) of GONG and MDI observations. The strongest signal was seen at 0.72 R⊙, with a weaker anticorrelated signal below the tachocline at 0.63 R⊙. At higher latitudes, there was also an apparent 1-year periodicity. The signal was more clearly seen in the GONG data, and due to the different temporal sample of the MDI data it was difficult to make a quantitative comparison, but the visual appearance of similar variations in both data sets was quite persuasive. Figure 31 extends the data up to the present for the equatorial locations just above and below the tachocline.
Because of the role of the tachocline region in the dynamo, as well as the coincidence of the period with that seen in some heliospheric and geomagnetic observations (Silverman and Shapiro, 1983; Richardson et al., 1994; Paularena et al., 1995), this claim attracted considerable interest, inspiring modelers such as Covas et al. (2001a) to try to build models in which different periods could exist at the top and bottom of the convection zone. However, Antia and Basu (2000) and Basu and Antia (2001), with a slightly different analysis of the same MDI and GONG data, reported finding no significant variations (Basu and Antia (2001) did see a signal somewhat similar to that reported by Howe et al. (2000b) but did not consider it significant).
Moreover, the periodic signal disappears in the post-2001 data even in the original authors’ analysis (Toomre et al., 2003; Howe et al., 2007), as shown in Figure 32, and it seems likely that the high-latitude 1-year period was an artifact. Intermittency in short-period variations is a known phenomenon in the geomagnetic-index data (Silverman and Shapiro, 1983) and does not in itself imply that the phenomenon was not real. It will be interesting to see whether the oscillation will reappear in the new solar cycle.
10.2 Tachocline jets
Christensen-Dalsgaard et al. (2004) searched for evidence of jets close to the tachocline, which are predicted, for example, by the model of Dikpati et al. (2004). Using GONG data they reported finding possible evidence of a jet at the tachocline, migrating equator-wards by about 30 degrees in two years but not at the same latitude as the surface activity belts. The significance and meaning of this finding remain unestablished.
10.3 Angular momentum variations
Given estimates of both density and rotation as functions of depth and latitude, one can calculate the solar angular momentum locally or globally. Of course, such calculations will reflect, and in some cases enhance, any errors in the input data, and should therefore be approached with caution.
Komm et al. (2003) investigated the angular momentum variation based on the inversions of GONG and MDI data used by Howe et al. (2000b, a) and found variations reflecting the torsional oscillation well into the convection zone and 1.3 year variations close to the tachocline. Because the density increases steeply with decreasing radius, variations at greater depths will be more strongly seen in the angular momentum than in the rotation rate, but it should be remembered that no new information has been added to the data.
Lanza (2007) approached the problem from the other direction, considering the role of angular momentum transport in the modeling of the torsional oscillation.
Antia et al. (2008) investigated temporal variations of the solar kinetic energy, angular momentum and higher-order gravitational multipole moments as derived from helioseismic inferences of the internal rotation rate; they found variations on the time scale of the solar cycle (but not the 1.3 year cycle), with some discrepancies between MDI and GONG results. They also speculate that the kinetic-energy changes might contribute to the observed irradiance variations during the solar cycle; however, it is not clear that such a contribution is needed, as the usual view is that the solar-cycle variation in irradiance can be modeled simply from the effects of sunspots and plage on the surface, as discussed, for example, by Jones et al. (2008).
11 Summary and Discussion
Since the 1970s, helioseismology has provided several insights into the interior solar rotation: the approximately-rigid rotation of the radiative interior; the differential rotation throughout the convection zone; the thin tachocline; the extension of the surface torsional oscillation throughout the convection zone. More than once, these discoveries have overturned theoretical expectations, inspiring modelers to improve their calculations in an effort to reproduce the observed behavior. Because of the surprising nature of many of the findings, it has been important to have more than one source of observations, so that it is possible to distinguish between real solar features — especially the unexpected ones — and systematic error.
It may be that in the future solar cycle 23, with MDI and GONG operating in parallel, will be seen as a golden age of helioseismology. At the time of writing, we eagerly anticipate the launch of the Solar Dynamics Observatory [SDO] with its Helioseismic and Magnetic Imager [HMI], a successor to MDI that will provide near-continuous helioseismic observations at higher resolutions than ever before and may help in unraveling the relationships between active region flows, magnetic fields, and geoeffective solar activity as well as providing a continued watch on the longer-term variations in the solar velocity fields. Sadly, however, current plans call for both GONG and MDI to cease to collect data soon after the successful launch of SDO, which would leave HMI without any independent cross-checks, while on the low-degree front the BiSON network has recently lost its funding and there are no new dedicated low-degree space-based instruments currently scheduled.
There are still areas — such as the strength of the near-surface shear at high latitudes, the rotation of the inner core, and any inhomogeneities and changes in the tachocline — that remain unclear. Furthermore, a complete numerical model of the solar dynamo — vital for any long-term predictive capability — is still lacking, and helioseismic observations still have an important part to play in constraining such models as they develop.
References
Altrock, R.C., 1997, “An ‘extended solar cycle’ as observed in Fe xiv”, Solar Phys., 170, 411–423. [ADS] (Cited on page 50.)
Andersen, B.N. and Maltby, P., 1983, “Has rapid solar core rotation been observed?”, Nature, 302, 808–810. [ADS] (Cited on page 25.)
Antia, H.M. and Basu, S., 2000, “Temporal Variations of the Rotation Rate in the Solar Interior”, Astrophys. J., 541, 442–448. [DOI], [ADS], [arXiv:astro-ph/0004335] (Cited on pages 42 and 53.)
Antia, H.M. and Basu, S., 2001, “Temporal Variations of the Solar Rotation Rate at High Latitudes”, Astrophys. J. Lett., 559, L67–L70. [DOI], [ADS], [arXiv:astro-ph/0108226] (Cited on page 42.)
Antia, H.M., Basu, S. and Chitre, S.M., 1998, “Solar internal rotation rate and the latitudinal variation of the tachocline”, Mon. Not. R. Astron. Soc., 298, 543–556. [ADS], [arXiv:astro-ph/9709083] (Cited on pages 31 and 32.)
Antia, H.M., Chitre, S.M. and Gough, D.O., 2008, “Temporal variations in the Sun’s rotational kinetic energy”, Astron. Astrophys., 477, 657–663. [DOI], [ADS], [arXiv:0711.0799] (Cited on page 55.)
Appourchaux, T., Toutain, T., Telljohann, U., Jiménez, A., Rabello-Soares, M.C., Andersen, B.N. and Jones, A.R., 1995, “Frequencies and splittings of low-degree solar p modes: results of the Luminosity Oscillations Imager”, Astron. Astrophys., 294, L13–L16. [ADS] (Cited on page 27.)
Appourchaux, T., Chang, H.-Y., Gough, D.O. and Sekii, T., 2000a, “On measuring low-degree p-mode frequency splitting with full-disc integrated data”, Mon. Not. R. Astron. Soc., 319, 365–376. [ADS] (Cited on page 28.)
Appourchaux, T., Fröhlich, C., Andersen, B., Berthomieu, G., Chaplin, W.J., Elsworth, Y., Finsterle, W., Gough, D.O., Hoeksema, J.T., Isaak, G.R., Kosovichev, A.G., Provost, J., Scherrer, P.H., Sekii, T. and Toutain, T., 2000b, “Observational Upper Limits to Low-Degree Solar g-Modes”, Astrophys. J., 538, 401–414. [DOI], [ADS] (Cited on page 30.)
Bachmann, K.T., Schou, J. and Brown, T.M., 1993, “Observations of intermediate degree solar oscillations: 1989 April–June”, Astrophys. J., 412, 870–879. [DOI], [ADS] (Cited on page 34.)
Backus, G.E. and Gilbert, J.F., 1968, “The Resolving Power of Gross Earth Data”, Geophys. J. R. Astr. Soc., 16, 169–205. [DOI], [ADS] (Cited on page 17.)
Backus, G.E. and Gilbert, J.F., 1970, “Uniqueness in the Inversion of Inaccurate Gross Earth Data”, Philos. Trans. R. Soc. London, Ser. A, 266, 123–192. [ADS] (Cited on page 17.)
Basu, S., 1997, “Seismology of the base of the solar convection zone”, Mon. Not. R. Astron. Soc., 288, 572–584. [ADS] (Cited on page 32.)
Basu, S. and Antia, H.M., 1997, “Seismic measurement of the depth of the solar convection zone”, Mon. Not. R. Astron. Soc., 287, 189–198. [ADS] (Cited on page 31.)
Basu, S. and Antia, H.M., 2000, “Solar Cycle Variations of Large-Scale Flows in the Sun”, Solar Phys., 192, 469–480. [ADS], [arXiv:astro-ph/0001294] (Cited on page 44.)
Basu, S. and Antia, H.M., 2001, “A study of possible temporal and latitudinal variations in the properties of the solar tachocline”, Mon. Not. R. Astron. Soc., 324, 498–508. [ADS], [arXiv:astro-ph/0101314] (Cited on pages 53 and 54.)
Basu, S. and Antia, H.M., 2003, “Changes in Solar Dynamics from 1995 to 2002”, Astrophys. J., 585, 553–565. [DOI], [ADS], [arXiv:astro-ph/0211548] (Cited on pages 31, 32, and 43.)
Basu, S., Antia, H.M. and Tripathy, S.C., 1999, “Ring Diagram Analysis of Near-Surface Flows in the Sun”, Astrophys. J., 512, 458–470. [DOI], [ADS], [arXiv:astro-ph/9809309] (Cited on page 41.)
Beck, J.G., 2000, “A comparison of differential rotation measurements — (Invited Review))”, Solar Phys., 191, 47–70. [ADS] (Cited on page 40.)
Beck, J.G., Gizon, L. and Duvall Jr, T.L., 2002, “A New Component of Solar Dynamics: North-South Diverging Flows Migrating toward the Equator with an 11 Year Period”, Astrophys. J. Lett., 575, L47–L50. [DOI], [ADS] (Cited on page 44.)
Bertello, L., Henney, C.J., Ulrich, R.K., Varadi, F., Kosovichev, A.G., Scherrer, P.H., Roca Cortés, T., Thiery, S., Boumier, P., Gabriel, A.H. and Turck-Chièze, S., 2000, “Comparison of Frequencies and Rotational Splittings of Solar Acoustic Modes of Low Angular Degree from Simultaneous MDI and GOLF Observations”, Astrophys. J., 535, 1066–1077. [DOI], [ADS] (Cited on page 27.)
Birch, A.C. and Gizon, L., 2005, “Local Helioseismology”, Living Rev. Solar Phys., 2, lrsp-2005-6. URL (accessed 30 January 2009): http://www.livingreviews.org/lrsp-2005-6 (Cited on pages 7 and 20.)
Birch, A.C. and Kosovichev, A.G., 1998, “Latitudinal Variation of Solar Subsurface Rotation Inferred from p-Mode Frequency Splittings Measured with SOI-MDI and GONG”, Astrophys. J. Lett., 503, L187–190. [DOI], [ADS] (Cited on page 36.)
Brandenburg, A., 2005, “The Case for a Distributed Solar Dynamo Shaped by Near-Surface Shear”, Astrophys. J., 625, 539–547. [DOI], [ADS], [arXiv:astro-ph/0502275] (Cited on page 41.)
Brandt, J.C., 1966, “Consequences of the Torque Exerted on the Sun by the Solar Wind”, Astrophys. J., 144, 1221–1222. [DOI], [ADS] (Cited on page 23.)
Brookes, J.R., Isaak, G.R. and van der Raay, H.B., 1976, “Observation of free oscillations of the Sun”, Nature, 259, 92–95. [ADS] (Cited on page 24.)
Brown, T.M., 1985, “Solar rotation as a function of depth and latitude”, Nature, 317, 591–594. [ADS] (Cited on pages 26, 33, and 38.)
Brown, T.M. and Morrow, C.A., 1987, “Depth and latitude dependence of solar rotation”, Astrophys. J. Lett., 314, L21–L26. [DOI], [ADS] (Cited on pages 31, 33, and 40.)
Brown, T.M., Stebbins, R.T. and Hill, H.A., 1978, “Long-period oscillations of the apparent solar diameter: Astronomical observations”, Astrophys. J., 223, 324–338. [DOI], [ADS] (Cited on page 24.)
Brown, T.M., Christensen-Dalsgaard, J., Dziembowski, W.A., Goode, P., Gough, D.O. and Morrow, C.A., 1989, “Inferring the Sun’s internal angular velocity from observed p-mode frequency splittings”, Astrophys. J., 343, 526–546. [DOI], [ADS] (Cited on pages 5, 26, 31, 33, 34, and 40.)
Browning, M.K., Miesch, M.S., Brun, A.S. and Toomre, J., 2006, “Dynamo Action in the Solar Convection Zone and Tachocline: Pumping and Organization of Toroidal Fields”, Astrophys. J. Lett., 648, L157–L160. [DOI], [ADS], [arXiv:astro-ph/0609153] (Cited on page 39.)
Brun, A.S., Miesch, M.S. and Toomre, J., 2004, “Global-scale turbulent convection and magnetic dynamo action in the solar envelope”, Astrophys. J., 614, 1073–1098. [ADS] (Cited on pages 38 and 39.)
Caudell, T.P. and Hill, H.A., 1980, “On the statistical significance of the reported phase coherence for solar oscillations”, Mon. Not. R. Astron. Soc., 193, 381–383. [ADS] (Cited on page 24.)
Chaplin, W.J., Elsworth, Y., Howe, R., Isaak, G.R., McLeod, C.P., Miller, B.A. and New, R., 1996a, “Solar core rotation: low-degree solar p-mode rotational splitting results from BiSON”, Mon. Not. R. Astron. Soc., 280, 849–853. [ADS] (Cited on pages 26 and 27.)
Chaplin, W.J., Elsworth, Y., Isaak, G.R., Lines, R., McLeod, C.P., Miller, B.A. and New, R., 1996b, “Low-frequency, low-degree solar p-mode measurements from recent BiSON data”, Mon. Not. R. Astron. Soc., 282, L15–L19. [ADS] (Cited on page 25.)
Chaplin, W.J., Elsworth, Y., Isaak, G.R., McLeod, C.P., Miller, B.A. and New, R., 1997, “Solar p-mode linewidths from recent BiSON helioseismological data”, Mon. Not. R. Astron. Soc., 288, 623–626. [ADS] (Cited on page 25.)
Chaplin, W.J., Christensen-Dalsgaard, J., Elsworth, Y., Howe, R., Isaak, G.R., Larsen, R.M., New, R., Schou, J., Thompson, M.J. and Tomczyk, S., 1999, “Rotation of the solar core from BiSON and LOWL frequency observations”, Mon. Not. R. Astron. Soc., 308, 405–414. [ADS] (Cited on page 29.)
Chaplin, W.J., Elsworth, Y., Isaak, G.R., Marchenkov, K.I., Miller, B.A. and New, R., 2001, “Rigid rotation of the solar core? On the reliable extraction of low-l rotational p-mode splittings from full-disc observations of the Sun”, Mon. Not. R. Astron. Soc., 327, 1127–1136. [DOI], [ADS] (Cited on pages 27 and 29.)
Chaplin, W.J., Sekii, T., Elsworth, Y. and Gough, D.O., 2004, “On the detectability of a rotationrate gradient in the solar core”, Mon. Not. R. Astron. Soc., 355, 535–542. [DOI], [ADS] (Cited on page 29.)
Chaplin, W.J., Appourchaux, T., Baudin, F., Boumier, P., Elsworth, Y., Fletcher, S.T., Fossat, E., García, R.A., Isaak, G.R., Jiménez, A., Jiménez-Reyes, S.J., Lazrek, M., Leibacher, J.W., Lochard, J., New, R., Pallé, P., Régulo, C., Salabert, D., Seghouani, N., Toutain, T. and Wachter, R., 2006, “Solar FLAG hare and hounds: on the extraction of rotational p-mode splittings from seismic, Sun-as-a-star data”, Mon. Not. R. Astron. Soc., 369, 985–996. [DOI], [ADS], [arXiv:astro-ph/0606748] (Cited on page 29.)
Charbonneau, P., Tomczyk, S., Schou, J. and Thompson, M.J., 1998, “The Rotation of the Solar Core Inferred by Genetic Forward Modeling”, Astrophys. J., 496, 1015–1030. [DOI], [ADS] (Cited on page 29.)
Charbonneau, P., Christensen-Dalsgaard, J., Henning, R., Larsen, R.M., Schou, J., Thompson, M.J. and Tomczyk, S., 1999, “Helioseismic Constraints on the Structure of the Solar Tachocline”, Astrophys. J., 527, 445–460. [DOI], [ADS] (Cited on pages 31 and 32.)
Chou, D.-Y. and Dai, D.-C., 2001, “Solar Cycle Variations of Subsurface Meridional Flows in the Sun”, Astrophys. J. Lett., 559, L175–L178. [DOI], [ADS] (Cited on page 44.)
Chou, D.-Y. and Ladenkov, O., 2005, “Evolution of Solar Subsurface Meridional Flows in the Declining Phase of Cycle 23”, Astrophys. J., 630, 1206–1212. [DOI], [ADS] (Cited on page 44.)
Chou, D.-Y., Sun, M.-T., Huang, T.-Y., Jiménez, A., Lai, S.-P., Chi, P.-J., Ou, K.-T., Wang, C.-C., Lu, J.-Y., Chu, A.-L., Niu, C.-S., Mu, T.-M., Chen, K.-R., Chou, Y.-P., Rabello-Soares, M.C., Ai, G.X., Wang, G.-P., Zirin, H., Marquette, W. and Nenow, J., 1995, “Taiwan Oscillation Network”, Solar Phys., 160, 237–243. [ADS] (Cited on page 22.)
Christensen-Dalsgaard, J. and Gough, D.O., 1976, “Towards a heliological inverse problem”, Nature, 259, 89–92. [ADS] (Cited on page 24.)
Christensen-Dalsgaard, J. and Schou, J., 1988, “Differential rotation in the solar interior”, in Seismology of the Sun and Sun-Like Stars, Symposium held in Puerto de la Cruz, Spain, 26–30 September 1988, (Ed.) Rolfe, E.J., vol. SP-286 of ESA Conference Proceedings, pp. 149–153, ESA, Noordwijk. [ADS] (Cited on page 34.)
Christensen-Dalsgaard, J., Schou, J. and Thompson, M.J., 1990, “A comparison of methods for inverting helioseismic data”, Mon. Not. R. Astron. Soc., 242, 353–369. [ADS] (Cited on pages 16 and 17.)
Christensen-Dalsgaard, J., Gough, D.O. and Thompson, M.J., 1991, “The depth of the solar convection zone”, Astrophys. J., 378, 413–437. [DOI], [ADS] (Cited on page 31.)
Christensen-Dalsgaard, J., Däppen, W., Ajukov, S.V., Anderson, E.R., Antia, H.M., Basu, S., Baturin, V.A., Berthomieu, G., Chaboyer, B., Chitre, S.M., Cox, A.N., Demarque, P., Donatowicz, J., Dziembowski, W.A., Gabriel, M., Gough, D.O., Guenther, D.B., Guzik, J.A., Harvey, J.W., Hill, F., Houdek, G., Iglesias, C.A., Kosovichev, A.G., Leibacher, J.W., Morel, P., Proffitt, C.R., Provost, J., Reiter, J., Rhodes Jr, E.J., Rogers, F.J., Roxburgh, I.W., Thompson, M.J. and Ulrich, R.K., 1996, “The Current State of Solar Modeling”, Science, 272, 1286–1292. [DOI], [ADS] (Cited on page 9.)
Christensen-Dalsgaard, J., Corbard, T., Dikpati, M., Gilman, P.A. and Thompson, M.J., 2004, “Detection of Jets and Associated Toroidal Fields in the Solar Tachocline”, in Helio- and Aster-oseismology: Towards a Golden Future, Proceedings of the SOHO 14/GONG 2004 Workshop, New Haven, Connecticut, USA, 12–16 July, 2004, (Ed.) Danesy, D., vol. SP-559 of ESA Conference Proceedings, pp. 376–380, ESA, Noordwijk. [ADS] (Cited on page 55.)
Claverie, A., Isaak, G.R., McLeod, C.P., van der Raay, H.B. and Roca Cortés, T., 1979, “Solar structure from global studies of the 5-minute oscillation”, Nature, 282, 591–594. [DOI], [ADS] (Cited on pages 21 and 24.)
Claverie, A., Isaak, G.R., McLeod, C.P., van der Raay, H.B. and Roca Cortés, T., 1981, “Rapid rotation of the solar interior”, Nature, 293, 443–445. [ADS] (Cited on page 25.)
Claverie, A., Isaak, G.R., McLeod, C.P., van der Raay, H.B., Pallé, P.L. and Roca Cortés, T., 1982, “Solar core rotation”, Nature, 299, 704–707. [ADS] (Cited on page 25.)
Claverie, A., Isaak, G.R., McLeod, C.P., van der Raay, B., Pallé, P.L. and Roca Cortés, T., 1984, “Continuous observation of solar oscillations from two suitably spaced ground stations”, Mem. Soc. Astron. Ital., 55, 63–66. [ADS] (Cited on page 21.)
Corbard, T. and Thompson, M.J., 2002, “The subsurface radial gradient of solar angular velocity from MDI f-mode observations”, Solar Phys., 205, 211–229. [ADS], [astro-ph/0110361] (Cited on page 40.)
Corbard, T., Berthomieu, G., Provost, J. and Morel, P., 1998a, “Inferring the equatorial solar tachocline from frequency splittings”, Astron. Astrophys., 330, 1149–1159. [ADS], [arXiv:astro-ph/9710319] (Cited on page 32.)
Corbard, T., Di Mauro, M.P. and Sekii, T. et al. (The GOLF Team), 1998b, “The Solar Internal Rotation from GOLF Splittings”, in Structure and Dynamics of the Interior of the Sun and Sun-like Stars, Proceedings of the SOHO 6/GONG 98 Workshop, Boston, USA, 1–4 June 1998, (Eds.) Korzennik, S., Wilson, A., vol. SP-418 of ESA Conference Proceedings, pp. 741–746, ESA, Noordwijk. [ADS] (Cited on page 29.)
Corbard, T., Blanc-Féraud, L., Berthomieu, G. and Provost, J., 1999, “Non linear regularization for helioseismic inversions. Application for the study of the solar tachocline”, Astron. Astrophys., 344, 696–708. [ADS], [arXiv:astro-ph/9901112] (Cited on pages 31 and 32.)
Couvidat, S., García, R.A., Turck-Chièze, S., Corbard, T., Henney, C.J. and Jiménez-Reyes, S., 2003, “The Rotation of the Deep Solar Layers”, Astrophys. J. Lett., 597, L77–L79. [DOI], [ADS], [arXiv:astro-ph/0309806] (Cited on page 29.)
Covas, E., Tavakol, R., Moss, D. and Tworkowski, A., 2000, “Torsional oscillations in the solar convection zone”, Astron. Astrophys., 360, L21–L24. [ADS], [arXiv:astro-ph/0010323] (Cited on page 51.)
Covas, E., Tavakol, R. and Moss, D., 2001a, “Dynamical variations of the differential rotation in the solar convection zone”, Astron. Astrophys., 371, 718–730. [DOI], [ADS], [arXiv:astro-ph/0012137] (Cited on pages 51 and 53.)
Covas, E., Tavakol, R., Vorontsov, S. and Moss, D., 2001b, “Spatiotemporal fragmentation and the uncertainties in the solar rotation law”, Astron. Astrophys., 375, 260–263. [DOI], [ADS] (Cited on page 51.)
Covas, E., Tavakol, R., Vorontsov, S. and Moss, D., 2002, “Erratum: Spatiotemporal fragmentation and the uncertainties in the solar rotation law”, Astron. Astrophys., 394, 1117–1117. [DOI], [ADS], [arXiv:astro-ph/0105211] (Cited on page 51.)
Covas, E., Moss, D. and Tavakol, R., 2004, “The influence of density stratification and multiple nonlinearities on solar torsional oscillations”, Astron. Astrophys., 416, 775–782. [DOI], [ADS], [arXiv:astro-ph/0312241] (Cited on page 51.)
Cuypers, J., 1980, “On the calculation of the frequency splitting of adiabatic nonradial stellar oscillations by slow differential rotation”, Astron. Astrophys., 89, 207–208. [ADS] (Cited on page 14.)
Delache, P. and Scherrer, P.H., 1983, “Detection of solar gravity mode oscillations”, Nature, 306, 651–653. [ADS] (Cited on page 30.)
Deubner, F.-L., 1975, “Observations of Low Wavenumber Nonradial Eigenmodes of the Sun”, Astron. Astrophys., 44, 371–375. [ADS] (Cited on page 7.)
Dicke, R.H., 1964, “The Sun’s Rotation and Relativity”, Nature, 202, 432–435. [ADS] (Cited on pages 23 and 24.)
Dicke, R.H., 1976, “Evidence for a solar distortion rotating with a period of 12.2 days”, Solar Phys., 47, 475–515. [ADS] (Cited on page 25.)
Dicke, R.H., 1983, “Evidence for a distorted solar core rotating with a 12.4-day period”, Nature, 303, 292–295. [ADS] (Cited on page 25.)
Dicke, R.H. and Goldenberg, H.M., 1967a, “Differential Rotation and the Solar Oblateness”, Nature, 214, 1294–1296. [ADS] (Cited on page 23.)
Dicke, R.H. and Goldenberg, H.M., 1967b, “Solar Oblateness and General Relativity”, Phys. Rev. Lett., 18, 313–316. [ADS] (Cited on pages 23 and 24.)
Dicke, R.H., Kuhn, J.R. and Libbrecht, K.G., 1986, “The variable oblateness of the Sun: Measurements of 1984”, Astrophys. J., 311, 1025–1030. [DOI], [ADS] (Cited on page 24.)
Dicke, R.H., Kuhn, J.R. and Libbrecht, K.G., 1987, “Is the solar oblateness variable? Measurements of 1985”, Astrophys. J., 318, 451–458. [DOI], [ADS] (Cited on page 24.)
Dikpati, M., Corbard, T., Thompson, M.J. and Gilman, P.A., 2002, “Flux Transport Solar Dynamos with Near-Surface Radial Shear”, Astrophys. J. Lett., 575, L41–L45. [DOI], [ADS] (Cited on page 41.)
Dikpati, M., Cally, P.S. and Gilman, P.A., 2004, “Linear Analysis and Nonlinear Evolution of Two-Dimensional Global Magnetohydrodynamic Instabilities in a Diffusive Tachocline”, Astrophys. J., 610, 597–615. [DOI], [ADS] (Cited on page 55.)
Durney, B.R., 1975, “A comparison of the meridional flows in the Sun’s convection zone, predicted by theories of the solar dynamo and differential rotation”, Astrophys. J., 199, 761–764. [ADS] (Cited on page 38.)
Durney, B.R., 2000, “On the Torsional Oscillations in Babcock-Leighton Solar Dynamo Models”, Solar Phys., 196, 1–18. [ADS] (Cited on page 51.)
Durrant, C.J. and Schröter, E.H., 1983, “Solar global velocity oscillations and active region rotation”, Nature, 301, 589–591. [DOI], [ADS] (Cited on page 25.)
Duvall Jr, T.L., 1979, “Large-scale solar velocity fields”, Solar Phys., 63, 3–15. [ADS] (Cited on page 38.)
Duvall Jr, T.L. and Harvey, J.W., 1984, “Rotational frequency splitting of solar oscillations”, Nature, 310, 19–22. [ADS] (Cited on pages 21, 25, and 33.)
Duvall Jr, T.L., Jones, H.P. and Harvey, J.W., 1983, “Solar oscillations with 13-day period”, Nature, 304, 517–518. [ADS] (Cited on page 25.)
Duvall Jr, T.L., Dziembowski, W.A., Goode, P.R., Gough, D.O., Harvey, J.W. and Leibacher, J.W., 1984, “Internal rotation of the Sun”, Nature, 310, 22–25. [ADS] (Cited on pages 21, 26, and 33.)
Duvall Jr, T.L., Harvey, J.W. and Pomerantz, M.A., 1986, “Latitude and depth variation of solar rotation”, Nature, 321, 500–501. [ADS] (Cited on pages 21 and 33.)
Duvall Jr, T.L., Harvey, J.W., Libbrecht, K.G., Popp, B.D. and Pomerantz, M.A., 1988, “Frequencies of solar p-mode oscillations”, Astrophys. J., 324, 1158–1171. [DOI], [ADS] (Cited on page 31.)
Dziembowski, W.A., Goode, P.R. and Libbrecht, K.G., 1989, “The radial gradient in the Sun’s rotation”, Astrophys. J. Lett., 337, L53–L57. [DOI], [ADS] (Cited on pages 31 and 34.)
Edmunds, M.G. and Gough, D.O., 1983, “Solar atmospheric temperature inhomogeneities induce a 13-day oscillation in full-disk Doppler measurements”, Nature, 302, 810–812. [ADS] (Cited on page 25.)
Eff-Darwich, A. and Korzennik, S.G., 1998, “The Rotation of the Solar Core: Compatibility of the Different Data Sets Available”, in Structure and Dynamics of the Interior of the Sun and Sun-like Stars, Proceedings of the SOHO 6/GONG 98 Workshop, Boston, USA, 1–4 June 1998, (Eds.) Korzennik, S., Wilson, A., vol. SP-418 of ESA Conference Proceedings, pp. 685–692, ESA, Noordwijk. [ADS] (Cited on page 29.)
Eff-Darwich, A., Korzennik, S.G. and Jiménez-Reyes, S.J., 2002, “Inversion of the Internal Solar Rotation Rate”, Astrophys. J., 573, 857–863. [DOI], [ADS] (Cited on pages 29 and 30.)
Elliott, J.R. and Gough, D.O., 1999, “Calibration of the Thickness of the Solar Tachocline”, Astrophys. J., 516, 475–481. [DOI], [ADS] (Cited on pages 31 and 32.)
Elsworth, Y., Howe, R., Isaak, G.R., McLeod, C.P. and New, R., 1990a, “Variation of low-order acoustic solar oscillations over the solar cycle”, Nature, 345, 322–324. [DOI], [ADS] (Cited on page 21.)
Elsworth, Y., Isaak, G.R., Jefferies, S.M., McLeod, C.P., New, R., Pallé, P.L., Régulo, C. and Roca Cortés, T., 1990b, “Linewidths of low-degree acoustic modes of the Sun”, Mon. Not. R. Astron. Soc., 242, 135–140. [ADS] (Cited on page 25.)
Elsworth, Y., Howe, R., Isaak, G.R., McLeod, C.P., Miller, B.A., New, R., Wheeler, S.J. and Gough, D.O., 1995, “Slow Rotation of the Sun’s Interior”, Nature, 376, 669–672. [DOI], [ADS] (Cited on pages 27 and 28.)
Elsworth, Y.P., Jefferies, S.M., McLeod, C.P., New, R., Pallé, P.L., van der Raay, H.B., Regulo, C. and Roca Cortés, T., 1989, “The 160 minute solar oscillation: an artifact?”, Astrophys. J., 338, 557–562. [DOI], [ADS] (Cited on page 24.)
Emilio, M., Bush, R.I., Kuhn, J.R. and Scherrer, P.H., 2007, “A Changing Solar Shape”, Astrophys. J. Lett., 660, L161–L163. [DOI], [ADS] (Cited on page 24.)
Fivian, M.D., Hudson, H.S., Lin, R.P. and Zahid, H.J., 2008, “A Large Excess in Apparent Solar Oblateness Due to Surface Magnetism”, Science, 322, 560–562. [DOI], [ADS] (Cited on page 24.)
Fletcher, S.T., Chaplin, W.J. and Elsworth, Y., 2003, “Use of genetic algorithms to determine low-rotational p-mode splittings at high frequencies”, Mon. Not. R. Astron. Soc., 346, 825–832. [DOI], [ADS] (Cited on page 29.)
Fossat, E., 1995, “IRIS Status Report”, in Helio- and Astro-Seismology from the Earth and Space, GONG 1994, Los Angeles, California, May 16–20, 1994, (Eds.) Ulrich, R.K., Rhodes Jr, E.J., Däppen, W., vol. 76 of ASP Conference Series, pp. 387–391, Astronomical Society of the Pacific, San Francisco. [ADS] (Cited on page 22.)
Fossat, E., Grec, G. and Harvey, J.W., 1981a, “Power Spectrum of Differential Refraction and Comparison with Solar Diameter Fluctuation Measurements”, Astron. Astrophys., 94, 95–99. [ADS] (Cited on page 24.)
Fossat, E., Grec, G. and Pomerantz, M., 1981b, “Solar pulsations observed from the geographic South Pole: Initial results”, Solar Phys., 74, 59–63. [ADS] (Cited on page 25.)
Fröhlich, C., Romero, J., Roth, H., Wehrli, C., Andersen, B.N., Appourchaux, T., Domingo, V., Telljohann, U., Berthomieu, G., Delache, P., Provost, J., Toutain, T., Crommelynck, D.A., Chevalier, A., Fichot, A., Däppen, W., Gough, D., Hoeksema, T., Jiménez, A., Gómez, M.F., Herreros, J.M., Roca Cortés, T., Jones, A.R., Pap, J.M. and Willson, R.C., 1995, “VIRGO: Experiment for Helioseismology and Solar Irradiance Monitoring”, Solar Phys., 162, 101–128. [ADS] (Cited on page 22.)
Gabriel, A.H., Grec, G., Charra, J., Robillot, J.-M., Roca Cortés, T., Turck-Chièze, S., Bocchia, R., Boumier, P., Cantin, M., Cespédes, E., Cougrand, B., Crétolle, J., Damé, L., Decaudin, M., Delache, P., Denis, N., Duc, R., Dzitko, H., Fossat, E., Fourmond, J.-J., García, R.A., Gough, D., Grivel, C., Herreros, J.M., Lagardère, H., Moalic, J.-P., Pallé, P.L., Pétrou, N., Sanchez, M., Ulrich, R.K. and van der Raay, H.B., 1995, “Global Oscillations at Low Frequency from the SOHO Mission (GOLF))”, Solar Phys., 162, 61–99. [ADS] (Cited on page 22.)
Gabriel, A.H., Baudin, F., Boumier, P., García, R.A., Turck-Chièze, S., Appourchaux, T., Bertello, L., Berthomieu, G., Charra, J., Gough, D.O., Pallié, P.L., Provost, J., Renaud, C., Robillot, J.-M., Roca Cortés, T., Thiery, S. and Ulrich, R.K., 2002, “A search for solar g modes in the GOLF data”, Astron. Astrophys., 390, 1119–1131. [DOI], [ADS] (Cited on page 30.)
Galloway, D.J. and Weiss, N.O., 1981, “Convection and magnetic fields in stars”, Astrophys. J., 243, 945–953. [DOI], [ADS] (Cited on page 38.)
García, R.A., Eff-Darwich, A., Korzennik, S.G., Couvidat, S., Henney, C.J. and Turck-Chièze, S., 2003, “Analysis of rotational frequency splittings sensitive to the rotation rate of the solar core”, in Local and Global Helioseismology: The Present and Future, Proceedings of SOHO 12/GONG+ 2002, 27 October–1 November 2002, Big Bear Lake, California, U.S.A., (Ed.) Sawaya-Lacoste, H., vol. SP-517 of ESA Conference Proceedings, pp. 271–274, ESA, Noordwijk. [ADS] (Cited on page 29.)
García, R.A., Corbard, T., Chaplin, W.J., Couvidat, S., Eff-Darwich, A., Jiménez-Reyes, S.J., Korzennik, S.G., Ballot, J., Boumier, P., Fossat, E., Henney, C.J., Howe, R., Lazrek, M., Lochard, J., Palle, P.L. and Turck-Chièze, S., 2004, “About the rotation of the solar radiative interior”, Solar Phys., 220, 269–285. [DOI], [ADS] (Cited on page 29.)
García, R.A., Turck-Chièze, S., Jiménez-Reyes, S.J., Ballot, J., Pallé, P.L., Eff-Darwich, A., Mathur, S. and Provost, J., 2007, “Tracking Solar Gravity Modes: The Dynamics of the Solar Core”, Science, 316, 1591–1593. [DOI], [ADS] (Cited on page 30.)
Gelly, B., Lazrek, M., Grec, G., Ayad, A., Schmider, F.X., Renaud, C., Salabert, D. and Fossat, E., 2002, “Solar p-modes from 1979 days of the GOLF experiment”, Astron. Astrophys., 394, 285–297. [DOI], [ADS] (Cited on page 27.)
Giles, P.M., Duvall Jr, T.L. and Scherrer, P.H., 1998, “Time-Distance Measurements of Subsurface Rotation and Meridional Flow”, in Structure and Dynamics of the Interior of the Sun and Sunlike Stars, Proceedings of the SOHO 6/GONG 98 Workshop, Boston, USA, 1–4 June 1998, (Eds.) Korzennik, S., Wilson, A., vol. SP-418 of ESA Conference Proceedings, pp. 775–780, ESA, Noordwijk. [ADS] (Cited on page 42.)
Gilman, P.A. and Foukal, P.V., 1979, “Angular velocity gradients in the solar convection zone”, Astrophys. J., 229, 1179–1185. [DOI], [ADS] (Cited on page 40.)
Gilman, P.A. and Howe, R., 2003, “Meridional Motion and the Slope of Isorotation Contours”, in Local and Global Helioseismology: The Present and Future, Proceedings of SOHO 12/GONG+ 2002, 27 October–1 November 2002, Big Bear Lake, California, U.S.A., (Ed.) Sawaya-Lacoste, H., vol. SP-517 of ESA Conference Proceedings, pp. 283–285, ESA, Noordwijk. [ADS] (Cited on page 36.)
Gilman, P.A. and Miller, J., 1981, “Dynamically consistent nonlinear dynamos driven by convection in a rotating spherical shell”, Astrophys. J. Suppl. Ser., 46, 211–238. [DOI], [ADS] (Cited on page 38.)
Gilman, P.A. and Miller, J., 1986, “Nonlinear convection of a compressible fluid in a rotating spherical shell”, Astrophys. J. Suppl. Ser., 61, 585–608. [DOI], [ADS] (Cited on page 38.)
Gilvarry, J.J. and Sturrock, P.A., 1967, “Solar Oblateness and the Perihelion Advances of Planets”, Nature, 216, 1283–1285. [ADS] (Cited on page 23.)
Gizon, L., Fossat, E., Lazrek, M., Cacciani, A., Ehgamberdiev, S., Gelly, B., Grec, G., Hoeksema, J.T., Khalikov, S., Pallé, P.L., Pantel, A., Régulo, C., Schmider, F.-X. and Wilson, P.R., 1997, “New IRIS constraints on the solar core rotation”, Astron. Astrophys., 317, L71–L74. [ADS] (Cited on page 27.)
Glatzmaier, G.A., 1985, “Numerical simulations of stellar convective dynamos. II. Field propagation in the convection zone”, Astrophys. J., 291, 300–307. [DOI], [ADS] (Cited on page 38.)
Goldreich, P. and Schubert, G., 1968, “A Theoretical Upper Bound to the Solar Oblateness”, Astrophys. J., 154, 1005–1010. [ADS] (Cited on page 23.)
Gough, D.O., 1982, “Evidence for an oblique magnetic solar rotator”, Nature, 298, 350–354. [ADS] (Cited on page 25.)
Gough, D.O. and McIntyre, M.E., 1998, “Inevitability of a magnetic field in the Sun’s radiative interior”, Nature, 394, 755–757. [DOI], [ADS] (Cited on page 32.)
Gough, D.O., Kosovichev, A.G., Sekii, T., Libbrecht, K.G. and Woodard, M.F., 1993, “The Form of the Angular Velocity in the Solar Convection Zone”, in GONG 1992: Seismic Investigation of the Sun and Stars, Proceedings of a conference held in Boulder, Colorado, August 11–14, 1993, (Ed.) Brown, T.M., vol. 42 of ASP Conference Series, pp. 213–216, Astronomical Society of the Pacific, San Francisco. [ADS] (Cited on page 34.)
Gough, D.O., Sekii, T. and Stark, P.B., 1996, “Inferring Spatial Variation of Solar Properties from Helioseismic Data”, Astrophys. J., 459, 779–791. [DOI], [ADS] (Cited on page 17.)
Grec, G. and Fossat, E., 1977, “Photospheric Oscillations. III. Search for Long Period Modes”, Astron. Astrophys., 55, 411–420. [ADS] (Cited on page 24.)
Grec, G., Fossat, E. and Pomerantz, M., 1980, “Solar oscillations: Full disk observations from the geographic South Pole”, Nature, 288, 541–544. [DOI], [ADS] (Cited on pages 21 and 25.)
Grec, G., Fossat, E. and Pomerantz, M.A., 1983, “Full-disk observations of solar oscillations from the geographic South Pole: Latest results”, Solar Phys., 82, 55–66. [ADS] (Cited on page 25.)
Haber, D.A., Hindman, B.W., Toomre, J., Bogart, R.S., Larsen, R.M. and Hill, F., 2002, “Evolving Submerged Meridional Circulation Cells within the Upper Convection Zone Revealed by Ring-Diagram Analysis”, Astrophys. J., 570, 855–864. [DOI], [ADS] (Cited on pages 44 and 48.)
Hansen, C.J., Cox, J.P. and van Horn, H.M., 1977, “The effects of differential rotation on the splitting of nonradial modes of stellar oscillation”, Astrophys. J., 217, 151–159. [ADS] (Cited on page 14.)
Harvey, J.W., Hill, F., Hubbard, R., Kennedy, J.R., Leibacher, J.W., Pintar, J.A., Gilman, P.A., Noyes, R.W., Title, A.M., Toomre, J., Ulrich, R.K., Bhatnagar, A., Kennewell, J.A., Marquette, W., Patróon, J., Saaá, O. and Yasukawa, E., 1996, “The Global Oscillation Network Group (GONG)) Project”, Science, 272, 1284–1286. [ADS] (Cited on page 22.)
Hill, F., 1988, “Rings and trumpets — Three-dimensional power spectra of solar oscillations”, Astrophys. J., 333, 996–1013. [DOI], [ADS] (Cited on page 44.)
Hill, F. and Howe, R., 1998, “Calculating the GONG Leakage Matrix”, in Structure and Dynamics of the Interior of the Sun and Sun-like Stars, Proceedings of the SOHO 6/GONG 98 Workshop, Boston, USA, 1–4 June 1998, (Eds.) Korzennik, S., Wilson, A., vol. SP-418 of ESA Conference Proceedings, pp. 225–230, ESA, Noordwijk. [ADS] (Cited on page 12.)
Hill, F., Deubner, F.-L. and Isaak, G.R., 1991a, “Oscillation observations”, in Solar Interior and Atmosphere, (Eds.) Cox, A.N., Livingston, W.C., Matthews, M.S., pp. 329–400, University of Arizona Press, Tucson. [ADS] (Cited on page 7.)
Hill, H., Fröhlich, C., Gabriel, M. and Kotov, V.A., 1991b, “Solar gravity modes”, in Solar Interior and Atmosphere, (Eds.) Cox, A.N., Livingston, W.C., Matthews, M.S., pp. 562–617, University of Arizona Press, Tucson. [ADS] (Cited on page 30.)
Hill, H.A., 1985, “Detection and classication of resolved multiplet members of the solar 5 minute oscillations through solar diameter-type observations”, Astrophys. J., 290, 765–781. [DOI], [ADS] (Cited on page 26.)
Hill, H.A. and Caudell, T.P., 1979, “Global oscillations of the Sun: Observed as oscillations in the apparent solar limb darkening function”, Mon. Not. R. Astron. Soc., 186, 327–342. [ADS] (Cited on page 24.)
Hill, H.A. and Stebbins, R.T., 1975, “The intrinsic visual oblateness of the Sun”, Astrophys. J., 200, 471–475. [ADS] (Cited on page 24.)
Hill, H.A., Clayton, P.D., Patz, D.L., Healy, A.W., Stebbins, R.T., Oleson, J.R. and Zanoni, C.A., 1974, “Solar Oblateness, Excess Brightness, and Relativity”, Phys. Rev. Lett., 33, 1497–1500. [ADS] (Cited on page 24.)
Hill, H.A., Bos, R.J. and Goode, P.R., 1982, “Preliminary Determination of the Sun’s Gravitational Quadrupole Moment from Rotational Splitting of Global Oscillations and its Relevance to Tests of General Relativity”, Phys. Rev. Lett., 49, 1794–1797. [ADS] (Cited on page 26.)
Howard, L.N., Moore, D.W. and Spiegel, E.A., 1967, “Solar Spin-Down Problem”, Nature, 214, 1297–1299. [ADS] (Cited on page 23.)
Howard, R. and LaBonte, B.J., 1980, “The Sun is observed to be a torsional oscillator with a period of 11 years”, Astrophys. J. Lett., 239, L33–L36. [DOI], [ADS] (Cited on pages 42 and 51.)
Howe, R. and Thompson, M.J., 1996, “On the use of the error correlation function in helioseismic inversions”, Mon. Not. R. Astron. Soc., 281, 1385–1392. [ADS] (Cited on page 16.)
Howe, R. and Thompson, M.J., 1998, “A strategy for fitting partially blended ridges in GONG solar p-mode spectra”, Astron. Astrophys. Suppl., 131, 539–548. [ADS] (Cited on page 12.)
Howe, R., Antia, H.M., Basu, S., Christensen-Dalsgaard, J., Korzennik, S.G., Schou, J. and Thompson, M.J., 1998, “The SOI-MDI High-Latitude Jet: The Evidence For and Against”, in Structure and Dynamics of the Interior of the Sun and Sun-like Stars, Proceedings of the SOHO 6/GONG 98 Workshop, Boston, USA, 1–4 June 1998, (Eds.) Korzennik, S., Wilson, A., vol. SP-418 of ESA Conference Proceedings, pp. 803–808, ESA, Noordwijk. [ADS] (Cited on page 36.)
Howe, R., Christensen-Dalsgaard, J., Hill, F., Komm, R.W., Larsen, R.M., Schou, J., Thompson, M.J. and Toomre, J., 2000a, “Deeply Penetrating Banded Zonal Flows in the Solar Convection Zone”, Astrophys. J. Lett., 533, L163–L166. [DOI], [ADS], [arXiv:astro-ph/0003121] (Cited on pages 42, 44, and 55.)
Howe, R., Christensen-Dalsgaard, J., Hill, F., Komm, R.W., Larsen, R.M., Schou, J., Thompson, M.J. and Toomre, J., 2000b, “Dynamic Variations at the Base of the Solar Convection Zone”, Science, 287, 2456–2460. [ADS] (Cited on pages 36, 37, 53, 54, and 55.)
Howe, R., Komm, R. and Hill, F., 2000c, “Variations in solar sub-surface rotation from GONG data 1995–1998”, Solar Phys., 192, 427–435. [ADS] (Cited on page 42.)
Howe, R., Christensen-Dalsgaard, J., Hill, F., Komm, R., Schou, J. and Thompson, M.J., 2005, “Solar Convection-Zone Dynamics, 1995–2004”, Astrophys. J., 634, 1405–1415. [DOI], [ADS] (Cited on pages 36, 37, 43, and 44.)
Howe, R., Komm, R., Hill, F., Ulrich, R.K., Haber, D.A., Hindman, B.W., Schou, J. and Thompson, M.J., 2006a, “Large-Scale Zonal Flows Near the Solar Surface”, Solar Phys., 235, 1–15. [DOI], [ADS] (Cited on pages 41, 42, and 50.)
Howe, R., Rempel, M., Christensen-Dalsgaard, J., Hill, F., Komm, R., Larsen, R.M., Schou, J. and Thompson, M.J., 2006b, “Solar Convection Zone Dynamics: How Sensitive Are Inversions to Subtle Dynamo Features?”, Astrophys. J., 649, 1155–1168. [DOI], [ADS] (Cited on pages 43, 44, and 52.)
Howe, R., Christensen-Dalsgaard, J., Hill, F., Komm, R., Schou, J., Thompson, M.J. and Toomre, J., 2007, “Temporal variations in solar rotation at the bottom of the convection zone: The current status”, Adv. Space Res., 40, 915–918. [DOI], [ADS] (Cited on page 54.)
Hughes, D.W., Rosner, R. and Weiss, N.O. (Eds.), 2007, The Solar Tachocline,Invited reviews from speakers at a workshop held at the Isaac Newton Institute, Cambridge, 8–12 November 2004, Cambridge University Press, Cambridge; New York. [ADS] (Cited on page 32.)
Iben Jr, I., 1976, “Solar oscillations as a guide to solar structure”, Astrophys. J. Lett., 204, L147–L150. [ADS] (Cited on page 24.)
Isaak, G.R., 1982, “Is the Sun an oblique magnetic rotator?”, Nature, 296, 130–131. [ADS] (Cited on page 25.)
Jiménez, A., Pérez Hernández, F., Claret, A., Pallé, P.L., Réegulo, C. and Roca Cortées, T., 1994, “The rotation of the solar core”, Astrophys. J., 435, 874–880. [DOI], [ADS] (Cited on page 27.)
Jones, H.P., Chapman, G.A., Harvey, K.L., Pap, J.M., Preminger, D.G., Turmon, M.J. and Walton, S.R., 2008, “A Comparison of Feature Classification Methods for Modeling Solar Irradiance Variation”, Solar Phys., 248, 323–337. [DOI], [ADS] (Cited on page 55.)
Köhler, H., 1974, “On Differential Rotation”, Solar Phys., 34, 11–14. [DOI], [ADS] (Cited on page 38.)
Komm, R., Howe, R., Durney, B.R. and Hill, F., 2003, “Temporal Variation of Angular Momentum in the Solar Convection Zone”, Astrophys. J., 586, 650–662. [DOI], [ADS] (Cited on page 55.)
Komm, R., Howe, R., Hill, F., González Hernández, I., Toner, C. and Corbard, T., 2005, “Ring Analysis of Solar Subsurface Flows and Their Relation to Surface Magnetic Activity”, Astrophys. J., 631, 636–646. [DOI], [ADS] (Cited on page 50.)
Komm, R.W., 1994, “Meridional flow and rotation of active regions”, Solar Phys., 149, 417–420. [ADS] (Cited on page 50.)
Komm, R.W., Howard, R.F. and Harvey, J.W., 1993a, “Torsional oscillation patterns in photospheric magnetic features”, Solar Phys., 143, 19–39. [ADS] (Cited on page +42.)
Komm, R.W., Howard, R.F. and Harvey, J.W., 1993b, “Meridional Flow of Small Photospheric Magnetic Features”, Solar Phys., 147, 207–223. [DOI], [ADS] (Cited on page 50.)
Korzennik, S.G., Cacciani, A., Rhodes Jr, E.J., Tomczyk, S. and Ulrich, R.K., 1988, “Inversion of the solar rotation rate versus depth and latitude”, in Seismology of the Sun and Sun-Like Stars, Symposium held in Puerto de la Cruz, Spain, 26–30 September 1988, (Ed.) Rolfe, E.J., vol. SP-286 of ESA Conference Proceedings, pp. 117–124, ESA, Noordwijk. [ADS] (Cited on page 34.)
Kosovichev, A.G., 1996, “Helioseismic Constraints on the Gradient of Angular Velocity at the Base of the Solar Convection Zone”, Astrophys. J. Lett., 469, L61–L64. [DOI], [ADS] (Cited on page 32.)
Kosovichev, A.G. and Schou, J., 1997, “Detection of Zonal Shear Flows beneath the Sun’s Surface from f-Mode Frequency Splitting”, Astrophys. J. Lett., 482, L207–L210. [DOI], [ADS] (Cited on page 42.)
Kosovichev, A.G., Schou, J., Scherrer, P.H., Bogart, R.S., Bush, R.I., Hoeksema, J.T., Aloise, J., Bacon, L., Burnette, A., de Forest, C., Giles, P.M., Leibrand, K., Nigam, R., Rubin, M., Scott, K., Williams, S.D., Basu, S., Christensen-Dalsgaard, J., Däappen, W., Rhodes Jr, E.J., Duvall Jr, T.L., Howe, R., Thompson, M.J., Gough, D.O., Sekii, T., Toomre, J., Tarbell, T.D., Title, A.M., Mathur, D., Morrison, M., Saba, J.L.R., Wolfson, C.J., Zayer, I. and Milford, P.N., 1997, “Structure and Rotation of the Solar Interior: Initial Results from the MDI Medium-L Program”, Solar Phys., 170, 43–61. [ADS] (Cited on pages 35 and 40.)
Kraft, R.P., 1967, “Studies of Stellar Rotation. V. The Dependence of Rotation on Age among Solar-Type Stars”, Astrophys. J., 150, 551–570. [ADS] (Cited on page 23.)
Kuhn, J.R., Bush, R.I., Scherrer, P.H. and Scheick, X., 1998, “The Sun’s shape and brightness”, Nature, 392, 155–157. [DOI], [ADS] (Cited on page 24.)
Küker, M., Rüdiger, G. and Pipin, V.V., 1996, “Solar torsional oscillations due to the magnetic quenching of the Reynolds stress”, Astron. Astrophys., 312, 615–623. [ADS] (Cited on page 51.)
LaBonte, B.J. and Howard, R., 1982, “Torsional waves on the sun and the activity cycle”, Solar Phys., 75, 161–178. [ADS] (Cited on pages 42, 50, and 51.)
Lanza, A.F., 2007, “Angular momentum conservation and torsional oscillations in the Sun and solar-like stars”, Astron. Astrophys., 471, 1011–1022. [DOI], [ADS], [arXiv:0706.1623] (Cited on page 55.)
Lazrek, M., Pantel, A., Fossat, E., Gelly, B., Schmider, F.X., Fierry-Fraillon, D., Grec, G., Loudagh, S., Ehgamberdiev, S., Khamitov, I., Hoeksema, J.T., Pallie, P.L. and Riegulo, C., 1996, “Is the Solar Core Rotating Faster or Slower Than the Envelope?”, Solar Phys., 166, 1–16. [DOI], [ADS] (Cited on pages 27 and 28.)
Lazrek, M., Baudin, F., Bertello, L., Boumier, P., Charra, J., Fierry-Fraillon, D., Fossat, E., Gabriel, A.H., García, R.A., Gelly, B., Gouiffes, C., Grec, G., Pallé, P.L., Pérez Hernández, F., Régulo, C., Renaud, C., Robillot, J.-M., Roca Cortés, T., Turck-Chièze, S. and Ulrich, R.K., 1997, “First results on p modes from GOLF experiment”, Solar Phys., 175, 227–246. [DOI], [ADS] (Cited on page 27.)
Libbrecht, K.G., 1986, “Is there an unusual solar core?”, Nature, 319, 753–755. [ADS] (Cited on page 26.)
Libbrecht, K.G., 1988a, “Solar p-mode phenomenology”, Astrophys. J., 334, 510–516. [DOI], [ADS] (Cited on page 25.)
Libbrecht, K.G., 1988b, “Solar p-mode frequency splittings”, in Seismology of the Sun and Sun-Like Stars, Symposium held in Puerto de la Cruz, Spain, 26–30 September 1988, (Ed.) Rolfe, E.J., vol. SP-286 of ESA Conference Proceedings, pp. 131–136, ESA, Noordwijk. [ADS] (Cited on page 34.)
Libbrecht, K.G., 1989, “Solar p-mode frequency splittings”, Astrophys. J., 336, 1092–1097. [DOI], [ADS] (Cited on pages 34 and 40.)
Libbrecht, K.G. and Kaufman, J.M., 1988, “Frequencies of high-degree solar oscillations”, Astrophys. J., 324, 1172–1183. [DOI], [ADS] (Cited on page 31.)
Libbrecht, K.G. and Woodard, M.F., 1990, “Solar-cycle effects on solar oscillation frequencies”, Nature, 345, 779–782. [DOI], [ADS] (Cited on page 21.)
Livingston, W., Milkey, R. and Slaughter, C., 1977, “Solar luminosity variation. I. C I 5380 as a temperature indicator and a search for global oscillations”, Astrophys. J., 211, 281–287. [ADS] (Cited on page 24.)
Loudagh, S., Provost, J., Berthomieu, G., Ehgamberdiev, S., Fossat, E., Gelly, B., Grec, G., Khalikov, S., Lazrek, M., Pallé, P., Réegulo, C., Sanchez, L. and Schmider, F.-X., 1993, “A measurement of the l = 1 solar rotational splitting”, Astron. Astrophys., 275, L25–L28. [ADS] (Cited on pages 27 and 28.)
Lydon, T.J. and Sofia, S., 1996, “A Measurement of the Shape of the Solar Disk: The Solar Quadrupole Moment, the Solar Octopole Moment, and the Advance of Perihelion of the Planet Mercury”, Phys. Rev. Lett., 76, 177–179. [DOI], [ADS] (Cited on page 24.)
Mathur, S., Turck-Chièze, S., Couvidat, S. and García, R.A., 2007, “On the Characteristics of the Solar Gravity Mode Frequencies”, Astrophys. J., 668, 594–602. [DOI], [ADS] (Cited on page 30.)
Mecheri, R., Abdelatif, T., Irbah, A., Provost, J. and Berthomieu, G., 2004, “New values of gravitational moments J2 and J4 deduced from helioseismology”, Solar Phys., 222, 191–197. [DOI], [ADS] (Cited on page 24.)
Miesch, M.S., 2005, “Large-Scale Dynamics of the Convection Zone and Tachocline”, Living Rev. Solar Phys., 2, lrsp-2005-1. URL (accessed January 2008): http://www.livingreviews.org/lrsp-2005-1 (Cited on page 32.)
Miesch, M.S., Brun, A.S., DeRosa, M.L. and Toomre, J., 2008, “Structure and Evolution of Giant Cells in Global Models of Solar Convection”, Astrophys. J., 673, 557–575. [DOI], [ADS], [arXiv:0707.1460] (Cited on pages 38 and 39.)
Musman, S. and Nye, A.H., 1977, “Global oscillations of the solar brightness”, Astrophys. J. Lett., 212, L95–L99. [ADS] (Cited on page 24.)
Pallée, P.L., Pérez Hernández, F., Réegulo, C. and Roca Cortés, T., 1988, “Rotational splitting of low L solar p-mode”, in Seismology of the Sun and Sun-Like Stars, Symposium held in Puerto de la Cruz, Spain, 26–30 September 1988, (Ed.) Rolfe, E.J., vol. SP-286 of ESA Conference Proceedings, pp. 125–130, ESA, Noordwijk. [ADS] (Cited on page 27.)
Pallée, P.L., Regulo, C. and Roca Cortés, T., 1989, “Solar cycle induced variations of the low L solar acoustic spectrum”, Astron. Astrophys., 224, 253–258. [ADS] (Cited on page +21.)
Parker, E.N., 1987, “The dynamo dilemma”, Solar Phys., 110, 11–21. [ADS] (Cited on page 38.)
Paularena, K.I., Szabo, A. and Richardson, J.D., 1995, “Coincident 1.3-year periodicities in the ap geomagnetic index and the solar wind”, Geophys. Res. Lett., 22, 3001–3004. [DOI], [ADS] (Cited on page 53.)
Pijpers, F.P. and Thompson, M.J., 1992, “Faster formulations of the optimally localized averages method for helioseismic inversions”, Astron. Astrophys., 262, L33–L36. [ADS] (Cited on pages 17 and 20.)
Pijpers, F.P. and Thompson, M.J., 1994, “The SOLA method for helioseismic inversion”, Astron. Astrophys., 281, 231–240. [ADS] (Cited on pages 17 and 20.)
Rempel, M., 2007, “Origin of Solar Torsional Oscillations”, Astrophys. J., 655, 651–659. [DOI], [ADS], [arXiv:astro-ph/0610221] (Cited on page 52.)
Rhodes Jr, E.J., Ulrich, R.K. and Deubner, F.-L., 1979, “A new technique for measuring solar rotation”, Astrophys. J., 227, 629–637. [DOI], [ADS] (Cited on page 40.)
Rhodes Jr, E.J., Cacciani, A., Korzennik, S., Tomczyk, S., Ulrich, R.K. and Woodard, M.F., 1990, “Depth and latitude dependence of the solar internal angular velocity”, Astrophys. J., 351, 687–700. [DOI], [ADS] (Cited on page 40.)
Richardson, J.D., Paularena, K.I., Belcher, J.W. and Lazarus, A.J., 1994, “Solar wind oscillations with a 1.3 year period”, Geophys. Res. Lett., 21, 1559–1560. [ADS] (Cited on page 53.)
Ritzwoller, M.H. and Lavely, E.M., 1991, “A unified approach to the helioseismic forward and inverse problems of differential rotation”, Astrophys. J., 369, 557–566. [DOI], [ADS] (Cited on page 11.)
Roxburgh, I.W., 1967, “Implications of the Oblateness of the Sun”, Nature, 213, 1077–1078. [ADS] (Cited on page 23.)
Rozelot, J.P. and Rösch, J., 1997, “An Upper Bound to the Solar Oblateness”, Solar Phys., 172, 11–18. [ADS] (Cited on page 23.)
Scherrer, P.H. and Wilcox, J.M., 1980a, “Doppler observations of solar rotation”, Astrophys. J. Lett., 239, L89–L92. [DOI], [ADS] (Cited on page 42.)
Scherrer, P.H. and Wilcox, J.M., 1980b, “Further Investigation of the Solar Torsional Oscillator with a Period of 11 Years”, Bull. Am. Astron. Soc., 12, 473–473. [ADS] (Cited on page 42.)
Scherrer, P.H., Wilcox, J.M. and Svalgaard, L., 1980, “The rotation of the Sun: Observations at Stanford”, Astrophys. J., 241, 811–819. [DOI], [ADS] (Cited on page 42.)
Scherrer, P.H., Bogart, R.S., Bush, R.I., Hoeksema, J.T., Kosovichev, A.G., Schou, J., Rosenberg, W., Springer, L., Tarbell, T.D., Title, A., Wolfson, C.J. and Zayer, I. et al. (MDI Engineering Team)), 1995, “The Solar Oscillations Investigation — Michelson Doppler Imager”, Solar Phys., 162, 129–188. [ADS] (Cited on page 22.)
Schou, J., 1999, “Migration of Zonal Flows Detected Using Michelson Doppler Imager f-Mode Frequency Splittings”, Astrophys. J. Lett., 523, L181–L184. [DOI], [ADS] (Cited on pages 42 and 44.)
Schou, J. and Brown, T.M., 1994a, “Generation of artificial helioseismic time-series”, Astron. Astrophys. Suppl., 107, 541–550. [ADS] (Cited on pages 11 and 12.)
Schou, J. and Brown, T.M., 1994b, “On the rotation rate in the solar convection zone”, Astrophys. J., 434, 378–383. [DOI], [ADS] (Cited on page 34.)
Schou, J., Christensen-Dalsgaard, J. and Thompson, M.J., 1992, “The resolving power of current helioseismic inversions for the Sun’s internal rotation”, Astrophys. J. Lett., 385, L59–L62. [DOI], [ADS] (Cited on pages 16 and 34.)
Schou, J., Christensen-Dalsgaard, J. and Thompson, M.J., 1994, “On comparing helioseismic two-dimensional inversion methods”, Astrophys. J., 433, 389–416. [DOI], [ADS] (Cited on pages 14, 16, and 17.)
Schou, J., Antia, H.M., Basu, S., Bogart, R.S., Bush, R.I., Chitre, S.M., Christensen-Dalsgaard, J., Di Mauro, M.P., Dziembowski, W.A., Eff-Darwich, A., Gough, D.O., Haber, D.A., Hoeksema, J.T., Howe, R., Korzennik, S.G., Kosovichev, A.G., Larsen, R.M., Pijpers, F.P., Scherrer, P.H., Sekii, T., Tarbell, T.D., Title, A.M., Thompson, M.J. and Toomre, J., 1998, “Helioseismic Studies of Differential Rotation in the Solar Envelope by the Solar Oscillations Investigation Using the Michelson Doppler Imager”, Astrophys. J., 505, 390–417. [DOI], [ADS] (Cited on pages 20, 35, 36, and 40.)
Schou, J., Howe, R., Basu, S., Christensen-Dalsgaard, J., Corbard, T., Hill, F., Komm, R., Larsen, R.M., Rabello-Soares, M.C. and Thompson, M.J., 2002, “A Comparison of Solar p-Mode Parameters from the Michelson Doppler Imager and the Global Oscillation Network Group: Splitting Coefficients and Rotation Inversions”, Astrophys. J., 567, 1234–1249. [DOI], [ADS] (Cited on pages 36 and 40.)
Schou, J. et al. (The SOI Internal Rotation Team)), 1998, “Solar Internal Rotation”, in New Eyes to See Inside the Sun and Stars, Proceedings of IAU Symposium 185, held in Kyoto, Japan, 18–22 August, 1997, (Eds.) Deubner, F.-L., Christensen-Dalsgaard, J., Kurtz, D.W., vol. 185 of IAU Symposia, pp. 141–148, Reidel, Dordrecht; Boston. [ADS] (Cited on page 42.)
Schüssler, M., 1981, “The solar torsional oscillation and dynamo models of the solar cycle”, Astron. Astrophys., 94, L17–L18. [ADS] (Cited on page 51.)
Scuflaire, R., Gabriel, M., Noels, A. and Boury, A., 1975, “Oscillatory periods in the Sun and theoretical models with or without mixing”, Astron. Astrophys., 45, 15–18. [ADS] (Cited on page 24.)
Sekii, T., 1991, “Two-dimensional inversion for solar internal rotation”, Publ. Astron. Soc. Japan, 43, 381–411. [ADS] (Cited on page 34.)
Severnyi, A.B., Kotov, V.A. and Tsap, T.T., 1976, “Observations of solar pulsations”, Nature, 259, 87–89. [ADS] (Cited on page 24.)
Silverman, S.M. and Shapiro, R., 1983, “Power spectral analysis of auroral occurrence frequency”, J. Geophys. Res., 88, 6310–6316. [ADS] (Cited on pages 53 and 54.)
Snodgrass, H.B., 1983, “Magnetic rotation of the solar photosphere”, Astrophys. J., 270, 288–299. [DOI], [ADS] (Cited on page 40.)
Snodgrass, H.B., 1984, “Separation of large-scale photospheric Doppler patterns”, Solar Phys., 94, 13–31. [ADS] (Cited on pages 36 and 40.)
Spiegel, E.A., 1972, “A History of Solar Rotation”, in Physics of the Solar System, 4th Summer Institute for Astronomy and Astrophysics, Stony Brook, New York, 1970, (Ed.) Rasool, S.I., vol. SP-300 of NASA Special Publication, pp. 61–87, National Aeronautics and Space Administration, Washington. [ADS] (Cited on page 31.)
Spiegel, E.A. and Zahn, J.-P., 1992, “The solar tachocline”, Astron. Astrophys., 265, 106–114. [ADS] (Cited on pages 31 and 32.)
Spruit, H.C., 2003, “Origin of the torsional oscillation pattern of solar rotation”, Solar Phys., 213, 1–21. [ADS], [astro-ph/0209146] (Cited on pages 51 and 52.)
Sturrock, P.A. and Gilvarry, J.J., 1967, “Solar Oblateness and Magnetic Field”, Nature, 216, 1280–1283. [ADS] (Cited on page 23.)
Tavakol, R., Covas, E., Moss, D. and Tworkowski, A., 2002, “Effects of boundary conditions on the dynamics of the solar convection zone”, Astron. Astrophys., 387, 1100–1106. [DOI], [ADS], [arXiv:astro-ph/0202440] (Cited on page 51.)
Thompson, M.J., Toomre, J., Anderson, E., Antia, H.M., Berthomieu, G., Burtonclay, D., Chitre, S.M., Christensen-Dalsgaard, J., Corbard, T., DeRosa, M.L., Genovese, C.R., Gough, D.O., Haber, D.A., Harvey, J.W., Hill, F., Howe, R., Korzennik, S.G., Kosovichev, A.G., Leibacher, J.W., Pijpers, F.P., Provost, J., Rhodes, E.J., Schou, J., Sekii, T., Stark, P.B. and Wilson, P., 1996, “Differential Rotation and Dynamics of the Solar Interior”, Science, 272, 1300–1305. [ADS] (Cited on pages 35 and 40.)
Thomson, D.J., Maclennan, C.G. and Lanzerotti, L.J., 1995, “Propagation of Solar Oscillations Through the Interplanetary Medium”, Nature, 376, 139–145. [DOI], [ADS] (Cited on page 30.)
Tomczyk, S., Cacciani, A. and Veitzer, S.A., 1993, “LOWL — An Instrument to Observe Low-Degree Solar Oscillations”, in Seismic Investigation of the Sun and Stars, GONG 1992, held in Boulder, Colorado, August 11–14, 1993, (Ed.) Brown, T.M., vol. 42 of ASP Conference Series, pp. 469–472, Astronomical Society of the Pacific, San Francisco. [ADS] (Cited on page 22.)
Tomczyk, S., Schou, J. and Thompson, M.J., 1995, “Measurement of the Rotation Rate in the Deep Solar Interior”, Astrophys. J. Lett., 448, L57–L60. [DOI], [ADS] (Cited on page 28.)
Toomre, J., Christensen-Dalsgaard, J., Howe, R., Larsen, R.M., Schou, J. and Thompson, M.J., 2000, “Time Variability of Rotation in Solar Convection Zone From SOI-MDI”, Solar Phys., 192, 437–448. [ADS] (Cited on page 42.)
Toomre, J., Christensen-Dalsgaard, J., Hill, F., Howe, R., Komm, R.W., Schou, J. and Thompson, M.J., 2003, “Transient oscillations near the solar tachocline”, in Local and Global Helioseismology: The Present and Future, Proceedings of SOHO 12/GONG+ 2002, 27 October–1 November 2002, Big Bear Lake, California, U.S.A., (Ed.) Sawaya-Lacoste, H., vol. SP-517 of ESA Conference Proceedings, pp. 409–412, ESA, Noordwijk. [ADS] (Cited on page 54.)
Toutain, T. and Fröhlich, C., 1992, “Characteristics of solar p-modes: results from the IPHIR experiment”, Astron. Astrophys., 257, 287–297. [ADS] (Cited on page 27.)
Toutain, T. and Kosovichev, A.G., 1994, “A new estimate of the solar core rotation from IPHIR”, Astron. Astrophys., 284, 265–268. [ADS] (Cited on page 27.)
Ulrich, R.K., 1998, “Identification of Very Large Scale Velocity Structures on the Solar Surface Using Mt. Wilson Synoptic Observations”, in Structure and Dynamics of the Interior of the Sun and Sun-like Stars, Proceedings of the SOHO 6/GONG 98 Workshop, Boston, USA, 1–4 June 1998, (Eds.) Korzennik, S., Wilson, A., vol. 418 of ESA Conference Proceedings, pp. 851–856, ESA, Noordwijk. [ADS] (Cited on page 42.)
Ulrich, R.K., 2001, “Very Long Lived Wave Patterns Detected in the Solar Surface Velocity Signal”, Astrophys. J., 560, 466–475. [DOI], [ADS] (Cited on pages 42 and 51.)
Ulrich, R.K. and Hawkins, G.W., 1981a, “The Solar Gravitational Figure — J2 and J4”, Astrophys. J., 246, 985–988. [DOI], [ADS] (Cited on page 24.)
Ulrich, R.K. and Hawkins, G.W., 1981b, “Erratum: The Solar Gravitational Figure — J2 and J4”, Astrophys. J., 249, 831–831. [DOI], [ADS] (Cited on page 24.)
van der Raay, H.B., 1988, “Long period solar oscillations”, in Seismology of the Sun and Sun-Like Stars, Symposium held in Puerto de la Cruz, Spain, 26–30 September 1988, (Ed.) Rolfe, E.J., vol. SP-286 of ESA Conference Proceedings, pp. 339–351, ESA, Noordwijk. [ADS] (Cited on page 30.)
Vorontsov, S.V., Christensen-Dalsgaard, J., Schou, J., Strakhov, V.N. and Thompson, M.J., 2002, “Helioseismic Measurement of Solar Torsional Oscillations”, Science, 296, 101–103. [DOI], [ADS] (Cited on pages 43 and 44.)
Wilson, P.R., 1992, “Helioseismology data and the solar dynamo”, Astrophys. J., 399, 294–299. [DOI], [ADS] (Cited on pages 38 and 40.)
Wilson, P.R. and Burtonclay, D., 1995, “Forward analysis of the BBSO frequency-splitting coefficients for 1986”, Astrophys. J., 438, 445–453. [DOI], [ADS] (Cited on page 12.)
Wilson, P.R., Burtonclay, D. and Li, Y., 1996a, “Calculations of the Solar Internal Angular Velocity for 1986–1990”, Astrophys. J., 457, 440–454. [DOI], [ADS] (Cited on page 32.)
Wilson, P.R., Burtonclay, D. and Li, Y., 1996b, “On the Inference of the Solar Internal Rotation Profile from Frequency-splitting Data”, Astrophys. J., 470, 621–628. [DOI], [ADS] (Cited on page 31.)
Woodard, M., 1984, “Upper limit on solar interior rotation”, Nature, 309, 530–532. [ADS] (Cited on page 26.)
Woodard, M. and Hudson, H.S., 1983a, “Frequencies, amplitudes and linewidths of solar oscillations from total irradiance observations”, Nature, 305, 589–593. [ADS] (Cited on page 25.)
Woodard, M. and Hudson, H.S., 1983b, “Solar oscillations observed in the total irradiance”, Solar Phys., 82, 67–73. [ADS] (Cited on page 25.)
Woodard, M.F. and Libbrecht, K.G., 1993, “Observations of time variation in the Sun’s rotation”, Science, 260, 1778–1781. [ADS] (Cited on page 42.)
Woodard, M.F. and Noyes, R.W., 1985, “Change of Solar Oscillation Eigenfrequencies with the Solar Cycle”, Nature, 318, 449–450. [ADS] (Cited on page 21.)
Woodard, M.F. and Noyes, R.W., 1988, “Time Variations of the Frequencies of Low-Degree Solar P-Modes”, in Advances in Helio- and Asteroseismology, Proceedings of IAU Symposium 123, July 7–11, 1986, Aarhus, Denmark, (Eds.) Christensen-Dalsgaard, J., Frandsen, S., vol. 123 of IAU Symposia, pp. 197–200, Reidel, Dordrecht; Boston. [ADS] (Cited on page 21.)
Yoshimura, H., 1981, “Solar cycle Lorentz force waves and the torsional oscillations of the Sun”, Astrophys. J., 247, 1102–1112. [DOI], [ADS] (Cited on page 51.)
Zaatri, A., Komm, R., González Hernández, I., Howe, R. and Corbard, T., 2006, “North-South Asymmetry of Zonal and Meridional Flows Determined From Ring Diagram Analysis of Gong ++ Data”, Solar Phys., 236, 227–244. [DOI], [ADS] (Cited on page 50.)
Zahn, J.-P., Talon, S. and Matias, J., 1997, “Angular momentum transport by internal waves in the solar interior”, Astron. Astrophys., 322, 320–328. [ADS], [arXiv:astro-ph/9611189] (Cited on page 32.)
Zhao, J. and Kosovichev, A.G., 2004, “Torsional Oscillation, Meridional Flows, and Vorticity Inferred in the Upper Convection Zone of the Sun by Time-Distance Helioseismology”, Astrophys. J., 603, 776–784. [DOI], [ADS] (Cited on pages 48 and 50.)
Acknowledgements
This review has made use of NASA’s Astrophysics Data System.
This work utilizes data obtained by the Global Oscillation Network Group (GONG) program, managed by the National Solar Observatory, which is operated by AURA, Inc. under a cooperative agreement with the National Science Foundation. The data were acquired by instruments operated by the Big Bear Solar Observatory, High Altitude Observatory, Learmonth Solar Observatory, Udaipur Solar Observatory, Instituto de Astrofísica de Canarias, and Cerro Tololo Interamerican Observatory. The Solar Oscillations Investigation (SOI) involving MDI is supported by NASA grant NAG5-13261 to Stanford University. SOHO is a mission of international cooperation between ESA and NASA. NSO/Kitt Peak magnetic data used here are produced cooperatively by NSF/NOAO, NASA/GSFC and NOAA/SEL.
The Mt. Wilson observations have been supported over several decades by a series of grants from NASA, NSF and ONR and are currently supported by NSF/ATM. The Mt. Wilson observatory is managed by the Mt. Wilson Institute under agreement with the Observatories of the Carnegie Institution of Washington.
BiSON has been funded by the U.K. Particle Physics and Astronomy Research Council.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Howe, R. Solar Interior Rotation and its Variation. Living Rev. Sol. Phys. 6, 1 (2009). https://doi.org/10.12942/lrsp-2009-1
Published:
DOI: https://doi.org/10.12942/lrsp-2009-1