Testing a toroidal magnetic field imaging method at the core-mantle boundary using a numerical dynamo model

Abstract

I quantitatively test a method of toroidal field imaging at the core-mantle boundary (CMB) using a synthetic magnetic field and core surface flow data from a 3-D self-consistent numerical dynamo model with a thin electrically conducting layer overlying the CMB, like the D ^″ layer. With complete knowledge of the core flow, the imaged toroidal field well reproduces the magnitude and pattern of the dynamo model toroidal field. However, quality of the imaging depends strongly on latitude. In particular, the amplitude and correlation between the dynamo model and the imaged toroidal fields decline substantially at low latitude. Such degradation in imaging quality is due to inability to account for the radial derivative of the toroidal field, that is, an effect of magnetic diffusion, which is not incorporated in the method.

Correspondence/findings

Introduction

The geomagnetic main field and its secular variation measured by orbiting satellites and at magnetic observatories correspond to those of the poloidal constituent, whereas the toroidal counterparts, which are bound to the core, are not observable above the core-mantle boundary (CMB). Constraining the strength, the spatial distribution and secular variation of the toroidal component of the geomagnetic field are essentially important to understand not only the dynamics of the geodynamo but also the electromagnetic (EM) core-mantle coupling, one of the possible mechanisms of decadal variation in the length of day (LOD) (Morrison [1979]).

Finite electric current flows in the mantle. The mantle electrical conductivity σ _m ∼ 1 S/m is small relative to that of the core σ _c ∼5×10⁵ S/m. In particular, the post-perovskite phase within the D ^″ layer above the CMB has greater electrical conductivity (approximately 10² S/m) (Ohta et al. [2008]). Therefore, the electric current or the corresponding toroidal field may leak into the mantle from the core, by which the EM coupling would occur. Some attempts to observationally constrain the toroidal magnetic field at the CMB have been pursued by electric potential measurements over distances larger than 1,000 km (Lanzerotti et al. [1993]; Shimizu et al. [1998]), whereas there are also some discussions on the consistency of such observations with dynamo theory (Levy and Pearce [1991]; Shimizu and Utada [2004]).

A global distribution of the toroidal field at the CMB can be estimated by a method based on a core flow model inverted from the radial components of the geomagnetic field and its secular variation via frozen-flux approximation (Roberts and Scott [1965]). Love and Bloxham ([1994]) determine the toroidal field at the CMB to account for LOD variation via the EM coupling assuming a steady core flow. However, it is found that only an implausibly strong and spatially complex toroidal field is consistent with flow advection and LOD variation (Love and Bloxham [1994]). Such a difficulty may be alleviated to some extent by taking time-dependence of the core flow into account (Holme [1998]). However, a fact must be kept in mind that the inverted core flows are in principle non-unique (Backus [1968]), and there is no way to know how well the toroidal field is retrieved properly from such a flow model.

Here, I test the method to infer the toroidal field at the CMB using a numerical dynamo model. It is a great advantage to utilize numerical dynamo modeling, because observations are limited, giving the poloidal field and indirectly the flow, while numerical dynamos have it all, including the toroidal field. Therefore, the major concern in this study is not an uncertainty arising from the non-uniqueness of the core flow estimation but that arising from several approximations to derive the toroidal field imaging method as introduced below.

Numerical model

I extend my numerical dynamo model (Takahashi et al. [2005], [2008]; Takahashi and Shimizu [2012]) to implement an electrically conducting mantle overlying the fluid outer core. Thermally driven convection alone is considered for simplicity, although thermo-chemical convection may be more appropriate to the Earth’s core (Takahashi [2014]). The model solves numerically the magnetohydrodynamic equations in a rotating spherical shell filled with an electrically conducting fluid obeying the Boussinesq approximation. The radii of the inner and outer cores are r _i and r _o , respectively, and the radius ratio r _i /r _o is 0.35. The solid inner core is assumed to be insulating.

The equations are non-dimensionalized in terms of the thickness of the shell d=r _o −r _i for length, the viscous diffusion time d²/ν for time, (2ρ μ η Ω)^1/2 for magnetic field, and h _i d for temperature, where ν is the kinematic viscosity, ρ is the fluid density, μ is the magnetic permeability in free space, η=1/(σ _c μ) is the core magnetic diffusivity, Ω is the angular velocity of the shell, and h _i is the temperature gradient at the inner core boundary (ICB). The non-dimensional equations to be solved are

$$\begin{array}{l}E\left(\frac{\partial \mathbf{u}}{\mathrm{\partial t}}+\mathbf{u}·\nabla \mathbf{u}-{\nabla }^2\mathbf{u}\right)=\mathbf{u}\times {\mathbf{e}}_z-\nabla p\\ +\mathrm{Ra\Theta }\frac{\mathbf{r}}{r_o}+\frac{1}{\mathit{\text{Pm}}}(\nabla \times \mathbf{B})\times \mathbf{B},\end{array}$$

(1)

$$\begin{array}{l}\frac{\partial \mathbf{B}}{\mathrm{\partial t}}=\frac{1}{\mathit{\text{Pm}}}{\nabla }^2\mathbf{B}+\nabla \times (\mathbf{u}\times \mathbf{B}),\end{array}$$

(2)

$$\begin{array}{l}\frac{\mathrm{\partial T}}{\mathrm{\partial t}}=\frac{1}{\mathit{\text{Pr}}}{\nabla }^{2}T-\mathbf{u}·\nabla T,\end{array}$$

(3)

$$\begin{array}{l}\nabla ·\mathbf{u}=\nabla ·\mathbf{B}=0.\end{array}$$

(4)

Here u, B, T, p, and e _z are the velocity field, the magnetic field, the temperature, the pressure, and the unit vector aligned to the rotation axis of the shell, respectively, while Θ is the temperature perturbation. The non-dimensional numbers in Equations 1, 2, and 3 are the Rayleigh number (Ra), the Ekman number (E), the magnetic Prandtl number (Pm), and the Prandtl number (Pr) defined by

$$\begin{array}{l}\mathit{\text{Ra}}=\frac{\alpha g_o{h}_i{d}^2}{2\mathrm{\Omega \nu }},E=\frac{\nu }{2\Omega d^2},\mathit{\text{Pm}}=\frac{\nu }{\eta },\mathit{\text{Pr}}=\frac{\nu }{\kappa },\end{array}$$

(5)

where α is the thermal expansion coefficient, g _o is the gravitational acceleration at the CMB, and κ is the thermal diffusivity.

I include a thin electrically conducting solid layer above the CMB to mimic the D ^″ layer. The thickness and electrical conductivity of the layer can be specified arbitrarily. The thickness of the layer δ adopted here is fixed at 5% of the core radius, δ/r _o =0.05, which corresponds to about 180 km for the Earth being comparable with D ^″ layer thickness (e.g., Schubert et al. [2001]). The electrical conductivity is assumed to be uniform within the layer. The conductivity of the layer is specified by the relative value with respect to the core conductivity as σ^∗=σ _m /σ _c . Within the layer, the magnetic diffusion equation

$$\begin{array}{l}\frac{\partial \mathbf{B}}{\mathrm{\partial t}}=\frac{1}{P{m}^{\ast }}{\nabla }^2\mathbf{B}\end{array}$$

(6)

is solved, where P m^∗ is the magnetic Prandtl number in the layer. Here, I examine the case at σ^∗=1/2,500, which is comparable with the electrical conductivity of the post-perovskite phase (Ohta et al. [2008]).

Spherical harmonic expansion is truncated at degree and order 95. The number of the radial grid points is 80 in the outer core and 20 in the D ^″ layer. In the outer core, radial derivatives are evaluated using combined compact finite differencing (Takahashi [2012]), whereas ordinary finite differencing is used in the D ^″ layer. At the ICB and CMB, no-slip and fixed heat flux boundary conditions are adopted for the velocity field and temperature, respectively. Continuity of the magnetic field and the tangential electric field is imposed at the CMB. At the top of the D ^″ layer, the toroidal field vanishes, while the poloidal field is smoothly connected with the potential field.

In the present study, I set R a=1,500, E=10⁻⁴, P m=2, and P r=1. The magnetic Reynolds number and the Elsasser number of the run using the mean values of the velocity and magnetic fields over the volume of the spherical shell are 103 and 1.79, respectively. The model lies in the dipole-dominated, non-reversing regime.

Toroidal field imaging method

To retrieve the CMB toroidal magnetic field, I adopt a procedure similar to Holme ([1998]) and Hagedoorn et al. ([2010]). I briefly describe the method (see Holme [1998] and Hagedoorn et al. [2010] for details). The magnetic field B is represented by a poloidal-toroidal decomposition,

$$\begin{array}{l}\mathbf{B}=\nabla \times \nabla \times \left(\mathcal{S}{\mathbf{e}}_r\right)+\nabla \times \left(\mathcal{T}{\mathbf{e}}_r\right),\end{array}$$

(7)

where , , and e _r are the poloidal scalar function, the toroidal scalar function, and the unit vector in the radial direction, respectively. To calculate the toroidal scalar function within the homogeneous D ^″, I solve the toroidal part of the diffusion equation

$$\begin{array}{l}\frac{\partial \mathcal{T}}{\mathrm{\partial t}}={\eta }_m{\nabla }^2\mathcal{T},\end{array}$$

(8)

where η _m =1/(σ _m μ). Assuming that the characteristic time scale of the magnetic field variation is much greater than the mantle magnetic diffusion time (Stix and Roberts [1984]), the temporal derivative term in the left-hand side of Equation 8 is dropped. Then, with an approximation that the D ^″ layer is so thin that the horizontal derivative terms are neglected with respect to the radial derivative term, Equation 8 is eventually reduced to

$$\begin{array}{l}\frac{{\partial }^2\mathcal{T}}{\partial r^2}=0.\end{array}$$

(9)

To solve the equation, boundary conditions at the top and bottom (CMB) of the D ^″ layer are required. The boundary condition on the tangential part of the electric field at the CMB can be written in the non-dimensional form as (Stix and Roberts [1984]; Holme [1998])

$$\begin{array}{l}\frac{1}{P{m}^{\ast }}\frac{1}{r_o^2}\frac{\partial }{\mathrm{\partial r}}\left(L^2\mathcal{T}\right){|}_{r=r_o}={\mathbf{e}}_r·{\nabla }_H\times \left(B_r\mathbf{u}\right){|}_{r=r_o}\\ +\frac{1}{\mathit{\text{Pm}}}\frac{1}{r_o^2}\frac{\partial }{\mathrm{\partial r}}\left(L^2\mathcal{T}\right){|}_{r=r_o},\end{array}$$

(10)

where ∇ _H is the surface gradient and L² is the angular momentum operator. According to the frozen-flux approximation (Roberts and Scott [1965]), the diffusional contribution in the right-hand side of Equation 10 is eliminated. Furthermore, by an approximation for a continuity of the horizontal electric field across the viscous boundary layer of the thickness d _ν , Equation 10 is reduced to

$$\begin{array}{l}\frac{1}{P{m}^{\ast }}\frac{1}{r_o^2}\frac{\partial }{\mathrm{\partial r}}\left(L^2\mathcal{T}\right){|}_{r=r_o}={\mathbf{e}}_r·{\nabla }_H\times \left(B_r\mathbf{u}\right){|}_{r=r_o-d_{\nu }}.\end{array}$$

(11)

By integrating the non-dimensional version of Equation 9 in terms of radius with boundary conditions of Equation 11 and $\mathcal{T}=0$ at r=r _o +δ, I have the expression for the toroidal function at the CMB

$$\begin{array}{l}\mathcal{T}\left(r_o\right)=-P{m}^{\ast }{r}_o^2\delta L^{-2}{\mathbf{e}}_r·{\nabla }_H\times \left(B_r\mathbf{u}\right){|}_{r=r_o-d_{\nu }}.\end{array}$$

(12)

Therefore, the toroidal field can, in principle, be retrieved from the knowledge of the radial magnetic field, the core flow, and the electrical conductivity (more precisely conductance, σ _m δ) of the D ^″ layer.

The discarded term in Equation 11 represents leakage of the electric current due to diffusion, which induces the leakage EM torque on the mantle. The influence of removing it on imaging quality is also examined. It is noted that the expression given in Equation 12 includes uncertainty regarding effective thickness of the viscous boundary layer. Hence, core flows at different depths beneath the CMB are tried for imaging.

Results

In the following, I show the results of an investigation with spatial resolution up to the truncation level of spherical harmonic expansion in the dynamo run and the results with the spatial resolution truncated at spherical harmonic degree 12 as in actual measurements. The former case is termed full resolution (FR) from hereafter, while the latter is termed truncated resolution (TR). To image the toroidal field at the CMB, I use snapshot data obtained from a dynamo model. In Figure 1, displayed are typical snapshots of the radial component of the magnetic field, B _r , at the CMB and the horizontal component of the velocity field, u _H , at r=0.984r _o in FR and TR. The depth is considered to be an effective one of the Ekman boundary layer as explained below. As seen in Figure 1, a predominantly dipolar dynamo solution is selected.

Figure 1

Synthetic data from a dynamo model. (a, b) The radial component of the magnetic field B _r at the CMB and (c, d) the core surface flow u _H at r=0.984r _o . Spatial resolution is truncated at spherical harmonic degree 12 in (b) and (d).

The azimuthal component of the toroidal field, B _{T ϕ} , is imaged at the CMB using B _r and u _H shown in Figure 1. The dynamo model toroidal field, $B_{\mathit{\text{T}}\varphi }^D$, and the corresponding imaged toroidal field, $B_{\mathit{\text{T}}\varphi }^I$, are compared in Figure 2. As a whole, the toroidal field is appreciably well reproduced with respect to the amplitude and spatial pattern in both the FR and TR cases. However, an obvious discrepancy is found around the equator, where the amplitude of the field tends to be underestimated, and the direction is even reversed in several places. Plots same as Figure 2 but for the co-latitudinal component of the toroidal field, B _{T θ} , are displayed in Figure 3. Since arguments for the component are similar to those for the azimuthal component, the azimuthal component alone is focused in the following.

Figure 2

Comparison of the imaged toroidal field with the dynamo model. The azimuthal component of the CMB toroidal magnetic field, B _{T ϕ} . (a, c) Dynamo model magnetic field $B_{\mathit{\text{T}}\varphi }^D$ and (b, d) the imaged magnetic field $B_{\mathit{\text{T}}\varphi }^I$. (a) and (b) are in FR, while (c) and (d) are in TR.

Figure 3

Comparison of the imaged toroidal field the with dynamo model. The co-latitudinal component of the CMB toroidal magnetic field, B _{T θ} . (a, c) Dynamo model magnetic field $B_{\mathit{\text{T}}\theta }^D$ and (b, d) the imaged magnetic field $B_{\mathit{\text{T}}\theta }^I$. (a) and (b) are in FR, while (c) and (d) are in TR.

I quantitatively evaluate the imaging method in terms of the magnitude and spatial pattern. In Figure 4, plots of the $B_{\mathit{\text{T}}\varphi }^I$ against the $B_{\mathit{\text{T}}\varphi }^D$ are shown. A proportional coefficient of the $B_{\mathit{\text{T}}\varphi }^I$ against the $B_{\mathit{\text{T}}\varphi }^D$ is calculated by way of principal component analysis, in which the first principal component is obtained by coordinate transformation maximizing the unbiased variance. In FR (Figure 4a), the $B_{\mathit{\text{T}}\varphi }^I$ tends to be slightly overestimated, whereas the $B_{\mathit{\text{T}}\varphi }^I$ is weaker than the $B_{\mathit{\text{T}}\varphi }^D$ in TR (Figure 4b). On the other hand, correlation coefficient is beyond 0.9 in both cases.

Figure 4

Quantitative evaluation of the imaged toroidal field B _{T ϕ} . Correspondence of the imaged toroidal field to the dynamo model toroidal field using u _H at r=0.984r _o in the case of (a) FR and (b) TR. The radial profiles of (c) amplitude ratio and (d) correlation coefficient. In (a) and (b), solid lines represent the amplitude ratio determined by the principal component analysis, and dashed lines represent the lines of slope one. In (c) and (d), black (gray) lines represent the case in FR (TR). Solid lines denote the mean values and dashed lines denote the mean ± 1 σ.

Then, the depth dependence of amplitude and correlation coefficient are examined. In the examination, u _H at different depths down to r=0.91r _o is used for imaging the CMB toroidal field, while for the other quantities such as B _r and $B_{\mathit{\text{T}}\varphi }^D$, those at the CMB are used. Regarding amplitude, the above-mentioned tendency remains unchanged with the depth below the viscous boundary layer in FR and TR cases (Figure 4c). In both cases, the ratio steeply increases from the CMB and reaches the maximum at r∼0.98r _o , then gradually declines (it is the reason why I show plots at r=0.984r _o as below the Ekman boundary layer of thickness d _ν ).

The correlation coefficient behaves differently in FR and TR (Figure 4d). In FR, the correlation coefficient takes the maximum at r∼0.98r _o just beneath the boundary layer like the amplitude ratio, whereas the maximum correlation in TR is obtained using a core flow slightly deeper than that in FR, although improvement in correlation is insignificant.

As stated above, quality of the imaging method seems to vary with latitude. To investigate the latitude dependence, I divide the CMB into three latitude bands: high-latitude band (|lat.|>60°), mid-latitude band (30°≤|lat.|≤60°), and low-latitude band (|lat.|<30°). Then, I calculate the amplitude ratio and correlation coefficient of each latitude band, which are given in Figure 5. It is confirmed that imaging quality is substantially poorer in the low-latitude band, compared with that in the high- and mid-latitude bands. It is also found that imaging degradation occurs in both FR and TR.

Figure 5

Radial profiles of the amplitude ratio and correlation of B _{T ϕ} . Mean values of (a) the amplitude ratio and (b) the correlation of the imaged toroidal field to dynamo model toroidal field for three latitude bands. Red lines represent those for high-latitude band, green lines mid-latitude band, and blue lines low-latitude band. Cases in FR (TR) are denoted by solid (dashed) lines.

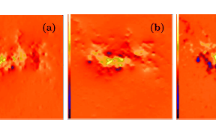
Based on Equation 10, I investigate why the imaging quality is poor in low latitude compared with other regions. Figure 6 shows maps of the left-hand side of Equation 10 at the CMB and the first term (advection) and second term (diffusion) in the right-hand side of Equation 10 but at r=0.984r _o . If neglecting the effects of diffusion in the core side was a good approximation, the leakage in the D ^″ layer (Figure 6a,b) would mostly be explained by the advection term beneath the boundary layer (Figure 6c,d). However, correspondence is not good in the low-latitude region, which is more clearly seen in TR than in FR. In addition, diffusion of the toroidal field seems to play a role in toroidal field generation in low-latitude (Figure 6f). Thus, I consider that degradation in imaging quality at low latitude is ascribed to the fact that I have neglected effects of diffusion in retrieving the toroidal field.

Figure 6

Effects of the toroidal field diffusion. Snapshots of (a, b) the diffusion term at the CMB (the left-hand side of the Equation 10), (c, d) the advection term at r=0.984r _o , and (e, f) the diffusion term at r=0.984r _o . (a, c, e) are in FR and (b, d, f) in TR.

Discussion and concluding remarks

In this study, I have examined the quality of the method to image the toroidal field at the CMB using numerical dynamo modeling. With perfect knowledge of the radial magnetic field, core surface flow, and the electrical conductivity of the D ^″ layer, the imaging method can reproduce much of the CMB toroidal field in terms of magnitude and pattern in FR and TR. However, the method fails to well reconstruct the toroidal field in low latitude, where the toroidal field generation is not dominated by the advection of the radial magnetic field alone. Since effects of magnetic diffusion are not taken into account in the present method, the low-latitude toroidal field could be underestimated by as much as 50%. Thus, the present method would provide us with a lower bound of the CMB toroidal field in the low-latitude region. Whether it is also the case in dynamo models at more Earth-like parameters, that is, lower E and Pm, should carefully be examined.

Contrary to the low latitude, the toroidal field in mid and high latitudes is generated by the process of flow advection. The recovered toroidal field tends to be slightly overestimated at FR in these regions. Such an overestimation may be the influence of an approximation that the D ^″ layer is a thin sheet, whereby the horizontal diffusion is neglected relative to the radial diffusion. Let l be the horizontal scale of the toroidal field in the D ^″. Then, the relative significance of the horizontal diffusion to the radial diffusion scales as D=(δ/l)². The condition D≪1 for verifying the thin sheet approximation is not met on small scales. Indeed, D∼1 at spherical harmonic degree n=20, given l∼r _o /n. It is anticipated that the overestimation is alleviated in a formulation without the thin sheet approximation. The effective conductance of the mantle will decrease with n, whereas Equation 12 includes the mantle conductance fixed at the D ^″ conductance. Nevertheless, the overestimation is no more than 20% in the FR case. This indicates the peripheral contribution of flow advection on small scales, which basically agrees with Figure seven in Holme ([1998]). Underestimation in TR arises probably from a different cause. The most likely one is that contributions from the small-scale components in B _r and u _H to the generation processes of the large-scale toroidal field are not properly represented in TR.

As to spatial correlation, the overall imaging quality is fairly well in both FR and TR cases (correlation coefficient is larger than 0.8) and not very sensitive to the depth of the core flows adopted for imaging as long as the core flow beneath the boundary layer is used.

In conclusion, any approximations adopted in the present method do not cause a serious problem. Therefore, the toroidal field imaging method based on Equation 12 may be applicable with some care to real observational data. However, the fact must be kept in mind before applying the method to observational data that the results in the present study are derived from the perfectly known core flows by forward modeling. Thus, effects must be understood on the ability and quality of the toroidal field reconstruction method of using inverted non-unique core flows with different a priori assumptions such as a purely toroidal flow (Whaler [1980]), steady flow (Voorhies and Backus [1985]), tangentially geostrophic flow (LeMouël [1984]), helical flow (Amit and Olson [2004]), and tangentially magnetostrophic flow (Asari and Lesur [2011]). This is obviously the next step of the study, where dynamo modeling would also be a help (Rau et al. [2000]; Amit et al. [2007]; Fournier et al. [2011]; Aubert and Fournier [2011]). Amit and Christensen ([2008]) find in numerical dynamos that poloidal field diffusion is roughly evenly distributed at all latitudes. The present model is also the case (although not shown). However, if poloidal field diffusion should also be concentrated at low latitude in the geomagnetic field, core flow inversions from geomagnetic secular variation may be affected, in particular, at low latitude (Amit and Christensen [2008]).

Besides, to reliably image the CMB toroidal magnetic field, an accurate electrical conductivity structure in the D ^″ layer (conductance) is required, which is to be determined by experimental, theoretical, and observational studies. Then, the magnitude of the toroidal field that may be imaged by the present method could be compared with other estimates based on torsional oscillations (Buffett et al. [2009]; Gillet et al. [2010]).