1 Introduction

Many phenomena in physics, biology, chemistry, mechanics, etc. are described by nonlinear partial differential equations. Nonlinear wave phenomena of dissipation, diffusion, reaction, and convection are very important, and they can be represented with a variety of nonlinear wave equations. The investigation of exact solutions of these equations will help ones to understand these phenomena better.

During the past several decades, many powerful and efficient methods have been proposed to obtain the exact solutions of nonlinear wave equations, such as inverse scattering method [1], Darboux and Bäcklund transformations [2, 3], the Hirota bilinear method [4], the tanh method [5], the extended tanh method [6], the sine-cosine method [7], the homogeneous balance method [8], the homotopy perturbation method [9, 10], the F-expansion method [11], the Exp-function expansion method [12, 13], the \((G'/G)\)-expansion method [14, 15], the Kudryashov method [16], the mapping method [17], the extended mapping method [18], and so on.

The above methods can be used to handle the nonlinear wave equations for single soliton solutions, but the multiple soliton solutions of the nonlinear wave equations can be obtained only by three different methods: the inverse scattering method, the Bäcklund transformation method, and the Hirota bilinear method. However, the Hirota bilinear method is rather heuristic and possesses significant features that make it be ideal for the determination of multiple soliton solutions for a wide class of the nonlinear wave equations [19–25]. When the Hirota bilinear method is used, computer symbolic systems such as Maple and Mathematica allow us to perform complicated and tedious calculations.

The Boussinesq equation is a well-known model of long water wave of moderate amplitude, describes one dimensional, weakly nonlinear internal wave which develops at the boundary between two immiscible fluids. In addition, the equation is a simplified model of the atmospheric movement equation which is applicable to mesoscale and quasi-incompressible fluid movement, which means important physical applications in hydrodynamics. The Boussinesq equation also is of considerable mathematic interests because of its rich mathematical structures. In the present research, we focus on the variant Boussinesq equations, which was derived by Sachs [26] in 1988 as a model for water waves:

$$ \left \{ \begin{array}{@{}l} H_{t}+(Hu)_{x}+u_{xxx} = 0,\\ u_{t}+H_{x}+uu_{x} = 0, \end{array} \right . $$
(1)

where \(u(x,t)\) is the velocity, \(H(x,t)\) is the height of free wave surface for fluid in the trough, and the subscripts denote partial derivatives. In the past years, many authors have studied Eq. (1). For example, Wang [27] solved Eq. (1) by the homogeneous balance method. Yan and Zhang [28] obtained new explicit and exact traveling wave solutions for Eq. (1) by an improved sine-cosine method and the Wu elimination method. Naz et al. [29] obtained the conservation laws for Eq. (1) by an interesting method of increasing the order of partial differential equations. Fan and Hon [30] uniformly constructed a series of traveling wave solutions for Eq. (1) by a new algebraic method. Lü [31] solved Eq. (1) by a general Jacobi elliptic function expansion method, and obtained Jacobi elliptic function solutions. Yuan et al. [32] constructed bifurcations of traveling wave solutions for Eq. (1) by the bifurcation theory of planar dynamical systems. Li et al. [33] obtained all possible smooth, cusped solitary wave solutions for Eq. (1) by the phase portrait analytical technique.

The above review shows that many works to obtain the exact solutions of Eq. (1) have been carried out in recent years, but the multiple soliton solutions for Eq. (1) have not been obtained. The existence of multiple soliton solutions often implies the integrability of the considered equations. The objectives of this paper are twofold. First, we aim to apply the Hirota bilinear method to handle Eq. (1). Second, we seek to establish multiple soliton solutions and multiple singular soliton solutions to confirm that Eq. (1) is completely integrable. The rest of this paper is organized as follows. In Section 2, the Hirota bilinear method for finding the multiple soliton solutions of the nonlinear wave equations is described. In Sections 3 and 4, the method to solve Eq. (1) is illustrated in detail. Multiple soliton solutions and multiple singular soliton solutions are obtained. In Section 5, some conclusions are given.

2 The Hirota bilinear method

The Hirota direct method is well known, and it gives soliton solutions by polynomials of exponentials. We only summarize the main steps as follows.

(i) Substituting

$$ u(x,t)=\mathtt{e}^{\theta_{i}}, \quad \theta_{i}=k_{i}x-c_{i}t, $$
(2)

into the linear terms of the equation under discussion to determine the dispersion relation between \(k_{i}\) and \(c_{i}\).

(ii) Substituting the single soliton solution

$$\begin{aligned}& u(x,t)=R\bigl[\ln f(x,t)\bigr]_{x}=R\frac{f_{x}}{f}, \end{aligned}$$
(3)
$$\begin{aligned}& u(x,t)=R\bigl[\ln f(x,t)\bigr]_{xx}=R\frac{ff_{xx}-f_{x}^{2}}{f^{2}}, \end{aligned}$$
(4)

or

$$ u(x,t)=R\biggl[\arctan\biggl(\frac{f(x,t)}{g(x,t)}\biggr) \biggr]_{x}=R\frac{f_{x}g-fg_{x}}{f^{2}+g^{2}} $$
(5)

into the equation under discussion to determine R, where

$$ f(x,t)=1+\mathtt{e}^{\theta_{1}}. $$
(6)

(iii) For a single soliton, we use

$$ f(x,t)=1+\mathtt{e}^{\theta_{1}}. $$
(7)

(iv) For two soliton solutions, we use

$$ f(x,t)=1+\mathtt{e}^{\theta_{1}}+\mathtt{e}^{\theta_{2}}+a_{12} \mathtt {e}^{\theta_{1}+\theta_{2}}. $$
(8)

(v) For three soliton solutions, we use

$$ f(x,t)=1+\mathtt{e}^{\theta_{1}}+\mathtt{e}^{\theta_{2}}+ \mathtt{e}^{\theta_{3}} +a_{12}\mathtt{e}^{\theta_{1}+\theta_{2}}+a_{23} \mathtt{e}^{\theta_{2}+\theta _{3}}+a_{13}\mathtt{e}^{\theta_{1}+\theta_{3}} +a_{123}\mathtt{e}^{\theta_{1}+\theta_{2}+\theta_{3}}. $$
(9)

If the obtained result shows that \(a_{123}=a_{12}a_{23}a_{13}\), then the equation gives multiple soliton solutions and the equation is integrable.

However, for multiple singular soliton solutions, we apply the following steps:

(i) For the dispersion relation, we use

$$ u(x,t)=\mathtt{e}^{\theta_{i}}, \quad \theta_{i}=k_{i}x-c_{i}t. $$
(10)

(ii) Next we substitute the single soliton solution

$$\begin{aligned}& u(x,t)=R\bigl[\ln f(x,t)\bigr]_{x}=R\frac{f_{x}}{f}, \end{aligned}$$
(11)
$$\begin{aligned}& u(x,t)=R\bigl[\ln f(x,t)\bigr]_{xx}=R\frac{ff_{xx}-f_{x}^{2}}{f^{2}}, \end{aligned}$$
(12)

or

$$ u(x,t)=R\biggl[\arctan\biggl(\frac{f(x,t)}{g(x,t)}\biggr) \biggr]_{x}=R\frac{f_{x}g-fg_{x}}{f^{2}+g^{2}} $$
(13)

into the equation under discussion to determine R, where

$$ f(x,t)=1-\mathtt{e}^{\theta_{1}}. $$
(14)

(iii) For a single soliton, we use

$$ f(x,t)=1-\mathtt{e}^{\theta_{1}}. $$
(15)

(iv) For two soliton solutions, we use

$$ f(x,t)=1-\mathtt{e}^{\theta_{1}}-\mathtt{e}^{\theta_{2}}+a_{12} \mathtt {e}^{\theta_{1}+\theta_{2}}. $$
(16)

(v) For three soliton solutions, we use

$$ f(x,t)=1-\mathtt{e}^{\theta_{1}}-\mathtt{e}^{\theta_{2}}- \mathtt{e}^{\theta_{3}} +a_{12}\mathtt{e}^{\theta_{1}+\theta_{2}}+a_{23} \mathtt{e}^{\theta_{2}+\theta _{3}}+a_{13}\mathtt{e}^{\theta_{1}+\theta_{3}} -a_{123}\mathtt{e}^{\theta_{1}+\theta_{2}+\theta_{3}}. $$
(17)

Other approaches will also be used for the multiple singular soliton solutions, as will be examined later.

3 Multiple soliton solutions of the variant Boussinesq equations

Substituting the following equations:

$$ \left \{ \begin{array}{@{}l} H(x,t) = A\mathtt{e}^{k_{i}x-c_{i}t},\\ u(x,t) = B\mathtt{e}^{k_{i}x-c_{i}t}, \end{array} \right . $$
(18)

into the linear terms of Eq. (1), we obtain the dispersion relation

$$ c_{i}=\pm k_{i}^{2}, $$
(19)

and as a result we have

$$ \theta_{i}=k_{i}x\mp k_{i}^{2}t, $$
(20)

where A and B are constants. Using the Cole-Hopf transformation method, we assume that the multiple solutions of Eq. (1) are

$$ \left \{ \begin{array}{@{}l} H(x,t) = R_{1}[\ln f(x,t)]_{xx}=R_{1}\frac{ff_{xx}-f_{x}^{2}}{f^{2}},\\ u(x,t) = R_{2}[\ln f(x,t)]_{x}=R_{2}\frac{f_{x}}{f}, \end{array} \right . $$
(21)

where \(f(x,t)\), for the single soliton solution, is given by

$$ f(x,t)=1+\mathtt{e}^{\theta_{1}}=1+\mathtt{e}^{k_{1}x\mp k_{1}^{2}t}. $$
(22)

Substituting Eq. (22) into Eq. (21), using the result from Eq. (1), and solving it for \(R_{1}\) and \(R_{2}\), we find

$$ R_{1}=R_{2}=2. $$
(23)

Substituting Eqs. (22)-(23) into Eq. (21) we obtain the single soliton solution

$$\begin{aligned}& \left \{ \begin{array}{@{}l} H(x,t) = \frac{2k_{1}^{2}\mathtt {e}^{k_{1}x+k_{1}^{2}t}}{(\mathtt{e}^{k_{1}^{2}t}+\mathtt{e}^{k_{1}x})^{2}},\\ u(x,t) = \frac{2k_{1}\mathtt {e}^{k_{1}x-k_{1}^{2}t}}{1+\mathtt{e}^{k_{1}x-k_{1}^{2}t}}, \end{array} \right . \end{aligned}$$
(24)
$$\begin{aligned}& \left \{ \begin{array}{@{}l} H(x,t) = \frac{2k_{1}^{2}\mathtt {e}^{k_{1}x+k_{1}^{2}t}}{(1+\mathtt{e}^{k_{1}x+k_{1}^{2}t})^{2}},\\ u(x,t) = \frac{2k_{1}\mathtt {e}^{k_{1}x+k_{1}^{2}t}}{1+\mathtt{e}^{k_{1}x+k_{1}^{2}t}}. \end{array} \right . \end{aligned}$$
(25)

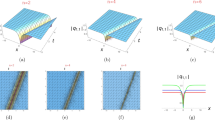
Figure 1 shows the single soliton solution for Eq. (1) for some special values of the solution’s parameters in Eq. (24).

Figure 1
figure 1

Plots of the solution described by Eq. ( 24 ). (a) The single soliton solution \(H(x,t)\) for \(k_{1}=0.4\). (b) The single soliton solution \(u(x,t)\) for \(k_{1}=0.4\).

Full size image

For two soliton solutions, we set

$$\begin{aligned} f(x,t)=1+\mathtt{e}^{\theta_{1}}+\mathtt{e}^{\theta_{2}}+a_{12} \mathtt {e}^{\theta_{1}+\theta_{2}} =1+\mathtt{e}^{k_{1}x\mp k_{1}^{2}t}+\mathtt{e}^{k_{2}x\mp k_{2}^{2}t}+a_{12} \mathtt {e}^{(k_{1}+k_{2})x\mp(k_{1}^{2}+k_{2}^{2})t}. \end{aligned}$$
(26)

Using Eqs. (23) and (26) into Eq. (21) and substituting the result into Eq. (1), we obtain the phase shift by

$$ a_{12}=0, $$
(27)

and hence we set

$$ a_{ij}=0,\quad 1\leq i < j \leq N. $$
(28)

The two soliton solutions are obtained by substituting Eqs. (26) and (27) into Eq. (21),

$$\begin{aligned}& \left \{ \begin{array}{@{}l} H(x,t) = \frac{2\mathtt {e}^{(k_{1}^{2}+k_{2}^{2})t}[k_{1}^{2}\mathtt{e}^{k_{1}x+k_{2}^{2}t}+(k_{1}-k_{2})^{2}\mathtt {e}^{(k_{1}+k_{2})x}+k_{2}^{2}\mathtt{e}^{k_{2}x+k_{1}^{2}t}]}{(\mathtt{e}^{(k_{1}^{2}+k_{2}^{2})t}+\mathtt{e}^{k_{1}x+k_{2}^{2}t}+\mathtt {e}^{k_{2}x+k_{1}^{2}t})^{2}},\\ u(x,t) = \frac{2(k_{1}\mathtt {e}^{k_{1}x-k_{1}^{2}t}+k_{2}\mathtt{e}^{k_{2}x-k_{2}^{2}t})}{1+\mathtt {e}^{k_{1}x-k_{1}^{2}t}+\mathtt{e}^{k_{2}x-k_{2}^{2}t}}, \end{array} \right . \end{aligned}$$
(29)
$$\begin{aligned}& \left \{ \begin{array}{@{}l} H(x,t) = \frac{2k_{1}^{2}\mathtt {e}^{k_{1}x+k_{1}^{2}t}+2\mathtt{e}^{k_{2}x+k_{2}^{2}t}[(k_{1}-k_{2})^{2}\mathtt {e}^{k_{1}x+k_{1}^{2}t}+k_{2}^{2}]}{(1+\mathtt{e}^{k_{1}x+k_{1}^{2}t}+\mathtt {e}^{k_{2}x+k_{2}^{2}t})^{2}},\\ u(x,t) = \frac{2(k_{1}\mathtt {e}^{k_{1}x+k_{1}^{2}t}+k_{2}\mathtt{e}^{k_{2}x+k_{2}^{2}t})}{1+\mathtt {e}^{k_{1}x+k_{1}^{2}t}+\mathtt{e}^{k_{2}x+k_{2}^{2}t}}. \end{array} \right . \end{aligned}$$
(30)

Figure 2 shows the two soliton solutions for Eq. (1) for some special values of the solution’s parameters in Eq. (29).

Figure 2
figure 2

Plots of the solution described by Eq. ( 29 ). (a) The two soliton solutions \(H(x,t)\) for \(k_{1}=0.4\), \(k_{2}=0.8\). (b) The two soliton solutions \(u(x,t)\) for \(k_{1}=0.4\), \(k_{2}=0.8\).

Full size image

For three soliton solutions, we set

$$\begin{aligned} f(x,t)=1+\mathtt{e}^{\theta_{1}}+\mathtt{e}^{\theta_{2}}+ \mathtt{e}^{\theta_{3}} =1+\mathtt{e}^{k_{1}x\mp k_{1}^{2}t}+\mathtt{e}^{k_{2}x\mp k_{2}^{2}t}+ \mathtt {e}^{k_{3}x\mp k_{3}^{2}t}. \end{aligned}$$
(31)

Proceeding as before, we find that the three soliton solutions are given by

$$\begin{aligned}& \left \{ \begin{array}{@{}l} H(x,t)= \frac{2\mathtt {e}^{-(k_{1}^{2}+k_{2}^{2}+k_{3}^{2})t}[k_{1}^{2}\mathtt{e}^{k_{1}x+(k_{2}^{2}+k_{3}^{2})t} +(k_{1}-k_{2})^{2}\mathtt{e}^{(k_{1}+k_{2})x+k_{3}^{2}t}+k_{2}^{2}\mathtt{e}^{k_{2}x+(k_{1}^{2}+k_{3}^{2})t} ]}{(1+\mathtt{e}^{k_{1}x- k_{1}^{2}t}+\mathtt{e}^{k_{2}x- k_{2}^{2}t}+\mathtt {e}^{k_{3}x- k_{3}^{2}t})^{2}}\\ \hphantom{ H(x,t)=}{} +\frac{2\mathtt {e}^{-(k_{1}^{2}+k_{2}^{2}+k_{3}^{2})t}[(k_{1}-k_{3})^{2}\mathtt{e}^{(k_{1}+k_{3})x+k_{2}^{2}t} +(k_{2}-k_{3})^{2}\mathtt{e}^{(k_{2}+k_{3})x+k_{1}^{2}t}+k_{3}^{2}\mathtt {e}^{k_{3}x+(k_{1}^{2}+k_{2}^{2})t}]}{(1+\mathtt{e}^{k_{1}x- k_{1}^{2}t}+\mathtt {e}^{k_{2}x- k_{2}^{2}t}+\mathtt{e}^{k_{3}x- k_{3}^{2}t})^{2}},\\ u(x,t)=\frac{2(k_{1}\mathtt{e}^{k_{1}x-k_{1}^{2}t}+k_{2}\mathtt {e}^{k_{2}x-k_{2}^{2}t}+k_{3}\mathtt{e}^{k_{3}x-k_{3}^{2}t})}{1+\mathtt{e}^{k_{1}x- k_{1}^{2}t}+\mathtt{e}^{k_{2}x- k_{2}^{2}t}+\mathtt {e}^{k_{3}x- k_{3}^{2}t}}, \end{array} \right . \end{aligned}$$
(32)
$$\begin{aligned}& \left \{ \begin{array}{@{}l} H(x,t)= \frac{2[k_{1}^{2}\mathtt {e}^{k_{1}x+k_{1}^{2}t} +(k_{1}-k_{2})^{2}\mathtt{e}^{(k_{1}+k_{2})x+(k_{1}^{2}+k_{2}^{2})t}+k_{2}^{2}\mathtt{e}^{k_{2}x+k_{2}^{2}t} ]}{(1+\mathtt{e}^{k_{1}x+ k_{1}^{2}t}+\mathtt{e}^{k_{2}x+ k_{2}^{2}t}+\mathtt {e}^{k_{3}x+ k_{3}^{2}t})^{2}}\\ \hphantom{H(x,t)=}{} +\frac{2[(k_{1}-k_{3})^{2}\mathtt{e}^{(k_{1}+k_{3})x+(k_{1}^{2}+k_{3}^{2})t} +(k_{2}-k_{3})^{2}\mathtt{e}^{(k_{2}+k_{3})x+(k_{2}^{2}+k_{3}^{2})t}+k_{3}^{2}\mathtt {e}^{k_{3}x+k_{3}^{2}t}]}{(1+\mathtt{e}^{k_{1}x+ k_{1}^{2}t}+\mathtt{e}^{k_{2}x+ k_{2}^{2}t}+\mathtt{e}^{k_{3}x+ k_{3}^{2}t})^{2}},\\ u(x,t)=\frac{2(k_{1}\mathtt{e}^{k_{1}x+k_{1}^{2}t}+k_{2}\mathtt {e}^{k_{2}x+k_{2}^{2}t}+k_{3}\mathtt{e}^{k_{3}x+k_{3}^{2}t})}{1+\mathtt{e}^{k_{1}x+ k_{1}^{2}t}+\mathtt{e}^{k_{2}x+ k_{2}^{2}t}+\mathtt {e}^{k_{3}x+ k_{3}^{2}t}}. \end{array} \right . \end{aligned}$$
(33)

Figure 3 shows the three soliton solutions for Eq. (1) for some special values of the solution’s parameters in Eq. (32).

Figure 3
figure 3

Plots of the solution described by Eq. ( 32 ). (a) The three soliton solutions \(H(x,t)\) for \(k_{1}=0.4\), \(k_{2}=0.8\), \(k_{3}=1.55\). (b) The three soliton solutions \(u(x,t)\) for \(k_{1}=0.4\), \(k_{2}=0.8\), \(k_{3}=1.45\).

Full size image

The three soliton solutions are obtained by substituting Eq. (31) into Eq. (21). This shows that Eq. (1) is completely integrable and N soliton solutions can be determined for \(H(x,t)\) and \(u(x,t)\), for finite N, where \(N\geq1\). Based on Eqs. (32) and (33), the general soliton solutions can be set as

$$\begin{aligned}& \left \{ \begin{array}{@{}l} H(x,t) = \frac{2[\sum_{i=1}^{N}k_{i}^{2}\mathtt{e}^{k_{i}x-k_{i}^{2}t}+\sum_{1\leq i< j\leq N}(k_{i}-k_{j})^{2}\mathtt{e}^{(k_{i}+k_{j})x-(k_{i}^{2}+k_{j}^{2})t}]}{(1+\sum_{i=1}^{N}\mathtt{e}^{k_{i}x-k_{i}^{2}t})^{2}},\\ u(x,t) = \frac{2\sum_{i=1}^{N}k_{i}\mathtt{e}^{k_{i}x-k_{i}^{2}t}}{1+\sum_{i=1}^{N}\mathtt {e}^{k_{i}x-k_{i}^{2}t}}, \end{array} \right . \end{aligned}$$
(34)
$$\begin{aligned}& \left \{ \begin{array}{@{}l} H(x,t) = \frac{2[\sum_{i=1}^{N}k_{i}^{2}\mathtt{e}^{k_{i}x+k_{i}^{2}t}+\sum_{1\leq i< j\leq N}(k_{i}-k_{j})^{2}\mathtt{e}^{(k_{i}+k_{j})x+(k_{i}^{2}+k_{j}^{2})t}]}{(1+\sum_{i=1}^{N}\mathtt{e}^{k_{i}x+k_{i}^{2}t})^{2}},\\ u(x,t) = \frac{2\sum_{i=1}^{N}k_{i}\mathtt{e}^{k_{i}x+k_{i}^{2}t}}{1+\sum_{i=1}^{N}\mathtt {e}^{k_{i}x+k_{i}^{2}t}}. \end{array} \right . \end{aligned}$$
(35)

4 Multiple singular soliton solutions of the variant Boussinesq equations

Substituting

$$ \left \{ \begin{array}{@{}l} H(x,t) = A\mathtt{e}^{k_{i}x-c_{i}t},\\ u(x,t) = B\mathtt{e}^{k_{i}x-c_{i}t}, \end{array} \right . $$
(36)

into the linear terms of Eq. (1) to find that the dispersion relation is

$$ c_{i}=\pm k_{i}^{2}, $$
(37)

and as a result we obtain

$$ \theta_{i}=k_{i}x\mp k_{i}^{2}t, $$
(38)

where A and B are constants. Using the Cole-Hopf transformation method, the multiple singular soliton solutions of Eq. (1) are assumed to be

$$ \left \{ \begin{array}{@{}l} H(x,t) = R_{1}[\ln f(x,t)]_{xx}=R_{1}\frac {ff_{xx}-f_{x}^{2}}{f^{2}},\\ u(x,t) = R_{2}[\ln f(x,t)]_{x}=R_{2}\frac{f_{x}}{f}, \end{array} \right . $$
(39)

where \(f(x,t)\), for the single singular soliton solution, is given by

$$ f(x,t)=1-\mathtt{e}^{\theta_{1}}=1-\mathtt{e}^{k_{1}x\mp k_{1}^{2}t}. $$
(40)

Substituting Eq. (39) into Eq. (1) and solving for \(R_{1}\) and \(R_{2}\) we find

$$ R_{1}=R_{2}=2. $$
(41)

This means that the single singular soliton solution is given by

$$\begin{aligned}& \left \{ \begin{array}{@{}l} H(x,t) = -\frac{2k_{1}^{2}\mathtt {e}^{k_{1}x+k_{1}^{2}t}}{(\mathtt{e}^{k_{1}^{2}t}-\mathtt{e}^{k_{1}x})^{2}},\\ u(x,t) = -\frac{2k_{1}\mathtt {e}^{k_{1}x-k_{1}^{2}t}}{1-\mathtt{e}^{k_{1}x-k_{1}^{2}t}}, \end{array} \right . \end{aligned}$$
(42)
$$\begin{aligned}& \left \{ \begin{array}{@{}l} H(x,t) = -\frac{2k_{1}^{2}\mathtt {e}^{k_{1}x+k_{1}^{2}t}}{(-1+\mathtt{e}^{k_{1}x+k_{1}^{2}t})^{2}},\\ u(x,t) = -\frac{2k_{1}\mathtt {e}^{k_{1}x+k_{1}^{2}t}}{1-\mathtt{e}^{k_{1}x+k_{1}^{2}t}}. \end{array} \right . \end{aligned}$$
(43)

Figure 4 shows the single singular soliton solution for Eq. (1) for some special values of the solution’s parameters in Eq. (42).

Figure 4
figure 4

Plots of the solution described by Eq. ( 42 ). (a) The single singular soliton solution \(H(x,t)\) for \(k_{1}=0.4\). (b) The single singular soliton solution \(u(x,t)\) for \(k_{1}=0.4\).

Full size image

For two singular soliton solutions, we set

$$\begin{aligned} f(x,t)=1-\mathtt{e}^{\theta_{1}}-\mathtt{e}^{\theta_{2}}+a_{12} \mathtt {e}^{\theta_{1}+\theta_{2}} =1-\mathtt{e}^{k_{1}x\mp k_{1}^{2}t}-\mathtt{e}^{k_{2}x\mp k_{2}^{2}t}+a_{12} \mathtt {e}^{(k_{1}+k_{2})x\mp(k_{1}^{2}+k_{2}^{2})t}. \end{aligned}$$
(44)

Using Eq. (44) into Eq. (39) and substituting the result into Eq. (1), we obtain the phase shift

$$ a_{12}=0, $$
(45)

and hence we set

$$ a_{ij}=0,\quad 1\leq i < j \leq N. $$
(46)

The two singular soliton solutions are obtained by substituting Eqs. (44) and (45) into Eq. (39), where we find

$$\begin{aligned}& \left \{ \begin{array}{@{}l} H(x,t) = -\frac{2\mathtt {e}^{(k_{1}^{2}+k_{2}^{2})t}[k_{1}^{2}\mathtt{e}^{k_{1}x+k_{2}^{2}t}-(k_{1}-k_{2})^{2}\mathtt {e}^{(k_{1}+k_{2})x}+k_{2}^{2}\mathtt{e}^{k_{2}x+k_{1}^{2}t}]}{(-\mathtt{e}^{(k_{1}^{2}+k_{2}^{2})t}+\mathtt{e}^{k_{1}x+k_{2}^{2}t}+\mathtt {e}^{k_{2}x+k_{1}^{2}t})^{2}},\\ u(x,t) = \frac{2(-k_{1}\mathtt {e}^{k_{1}x-k_{1}^{2}t}-k_{2}\mathtt{e}^{k_{2}x-k_{2}^{2}t})}{1-\mathtt {e}^{k_{1}x-k_{1}^{2}t}-\mathtt{e}^{k_{2}x-k_{2}^{2}t}}, \end{array} \right . \end{aligned}$$
(47)
$$\begin{aligned}& \left \{ \begin{array}{@{}l} H(x,t) = -\frac{2k_{1}^{2}\mathtt {e}^{k_{1}x+k_{1}^{2}t}-2\mathtt{e}^{k_{2}x+k_{2}^{2}t}[(k_{1}-k_{2})^{2}\mathtt {e}^{k_{1}x+k_{1}^{2}t}+k_{2}^{2}]}{(-1+\mathtt{e}^{k_{1}x+k_{1}^{2}t}+\mathtt {e}^{k_{2}x+k_{2}^{2}t})^{2}},\\ u(x,t) = -\frac{2(k_{1}\mathtt {e}^{k_{1}x+k_{1}^{2}t}+k_{2}\mathtt{e}^{k_{2}x+k_{2}^{2}t})}{1-\mathtt {e}^{k_{1}x+k_{1}^{2}t}-\mathtt{e}^{k_{2}x+k_{2}^{2}t}}. \end{array} \right . \end{aligned}$$
(48)

Figure 5 shows the two singular soliton solutions for Eq. (1) for some special values of the solution’s parameters in Eq. (47).

Figure 5
figure 5

Plots of the solution described by Eq. ( 47 ). (a) The two singular soliton solutions \(H(x,t)\) for \(k_{1}=0.4\), \(k_{2}=0.8\). (b) The two singular soliton solutions \(u(x,t)\) for \(k_{1}=0.4\), \(k_{2}=0.8\).

Full size image

For three singular soliton solutions, we set

$$\begin{aligned} f(x,t)=1-\mathtt{e}^{\theta_{1}}-\mathtt{e}^{\theta_{2}}- \mathtt{e}^{\theta_{3}} =1-\mathtt{e}^{k_{1}x\mp k_{1}^{2}t}-\mathtt{e}^{k_{2}x\mp k_{2}^{2}t}- \mathtt {e}^{k_{3}x\mp k_{3}^{2}t}. \end{aligned}$$
(49)

Proceeding as before, we find the following three singular soliton solutions:

$$\begin{aligned}& \left \{ \begin{array}{@{}l} H(x,t)= \frac{2\mathtt {e}^{-(k_{1}^{2}+k_{2}^{2}+k_{3}^{2})t}[-k_{1}^{2}\mathtt{e}^{k_{1}x+(k_{2}^{2}+k_{3}^{2})t} +(k_{1}-k_{2})^{2}\mathtt{e}^{(k_{1}+k_{2})x+k_{3}^{2}t}-k_{2}^{2}\mathtt{e}^{k_{2}x+(k_{1}^{2}+k_{3}^{2})t} ]}{(1-\mathtt{e}^{k_{1}x- k_{1}^{2}t}-\mathtt{e}^{k_{2}x- k_{2}^{2}t}-\mathtt {e}^{k_{3}x- k_{3}^{2}t})^{2}}\\ \hphantom{ H(x,t)=}{}+\frac{2\mathtt {e}^{-(k_{1}^{2}+k_{2}^{2}+k_{3}^{2})t}[(k_{1}-k_{3})^{2}\mathtt{e}^{(k_{1}+k_{3})x+k_{2}^{2}t} +(k_{2}-k_{3})^{2}\mathtt{e}^{(k_{2}+k_{3})x+k_{1}^{2}t}-k_{3}^{2}\mathtt {e}^{k_{3}x+(k_{1}^{2}+k_{2}^{2})t}]}{(1-\mathtt{e}^{k_{1}x- k_{1}^{2}t}-\mathtt {e}^{k_{2}x- k_{2}^{2}t}-\mathtt{e}^{k_{3}x- k_{3}^{2}t})^{2}},\\ u(x,t)=-\frac{2(k_{1}\mathtt{e}^{k_{1}x-k_{1}^{2}t}+k_{2}\mathtt {e}^{k_{2}x-k_{2}^{2}t}+k_{3}\mathtt{e}^{k_{3}x-k_{3}^{2}t})}{1-\mathtt{e}^{k_{1}x- k_{1}^{2}t}-\mathtt{e}^{k_{2}x- k_{2}^{2}t}-\mathtt {e}^{k_{3}x- k_{3}^{2}t}}, \end{array} \right . \end{aligned}$$
(50)
$$\begin{aligned}& \left \{ \begin{array}{@{}l} H(x,t)= \frac{2[-k_{1}^{2}\mathtt {e}^{k_{1}x+k_{1}^{2}t} +(k_{1}-k_{2})^{2}\mathtt{e}^{(k_{1}+k_{2})x+(k_{1}^{2}+k_{2}^{2})t}-k_{2}^{2}\mathtt{e}^{k_{2}x+k_{2}^{2}t} ]}{(1-\mathtt{e}^{k_{1}x+ k_{1}^{2}t}-\mathtt{e}^{k_{2}x+ k_{2}^{2}t}-\mathtt {e}^{k_{3}x+ k_{3}^{2}t})^{2}}\\ \hphantom{H(x,t)=}{}+\frac{2[(k_{1}-k_{3})^{2}\mathtt{e}^{(k_{1}+k_{3})x+(k_{1}^{2}+k_{3}^{2})t} +(k_{2}-k_{3})^{2}\mathtt{e}^{(k_{2}+k_{3})x+(k_{2}^{2}+k_{3}^{2})t}-k_{3}^{2}\mathtt {e}^{k_{3}x+k_{3}^{2}t}]}{(1-\mathtt{e}^{k_{1}x+ k_{1}^{2}t}-\mathtt{e}^{k_{2}x+ k_{2}^{2}t}-\mathtt{e}^{k_{3}x+ k_{3}^{2}t})^{2}},\\ u(x,t)=-\frac{2(k_{1}\mathtt{e}^{k_{1}x+k_{1}^{2}t}+k_{2}\mathtt {e}^{k_{2}x+k_{2}^{2}t}+k_{3}\mathtt{e}^{k_{3}x+k_{3}^{2}t})}{1-\mathtt{e}^{k_{1}x+ k_{1}^{2}t}-\mathtt{e}^{k_{2}x+ k_{2}^{2}t}-\mathtt {e}^{k_{3}x+ k_{3}^{2}t}}. \end{array} \right . \end{aligned}$$
(51)

Figure 6 shows the three singular soliton solutions for Eq. (1) for some special values of the solution’s parameters in Eq. (50).

Figure 6
figure 6

Plots of the solution described by Eq. ( 50 ). (a) The three singular soliton solutions \(H(x,t)\) for \(k_{1}=0.4\), \(k_{2}=0.8\), \(k_{3}=1.55\). (b) The three singular soliton solutions \(u(x,t)\) for \(k_{1}=0.4\), \(k_{2}=0.8\), \(k_{3}=1.45\).

Full size image

Based on the last result, we can set the general singular soliton solutions as

$$\begin{aligned}& \left \{ \begin{array}{@{}l} H(x,t) = \frac{2[-\sum_{i=1}^{N}k_{i}^{2}\mathtt{e}^{k_{i}x-k_{i}^{2}t}+\sum_{1\leq i< j\leq N}(k_{i}-k_{j})^{2}\mathtt{e}^{(k_{i}+k_{j})x-(k_{i}^{2}+k_{j}^{2})t}]}{(1-\sum_{i=1}^{N}\mathtt{e}^{k_{i}x-k_{i}^{2}t})^{2}},\\ u(x,t) = -\frac{2\sum_{i=1}^{N}k_{i}\mathtt{e}^{k_{i}x-k_{i}^{2}t}}{1-\sum_{i=1}^{N}\mathtt {e}^{k_{i}x-k_{i}^{2}t}}, \end{array} \right . \end{aligned}$$
(52)
$$\begin{aligned}& \left \{ \begin{array}{@{}l} H(x,t) = \frac{2[-\sum_{i=1}^{N}k_{i}^{2}\mathtt{e}^{k_{i}x+k_{i}^{2}t}+\sum_{1\leq i< j\leq N}(k_{i}-k_{j})^{2}\mathtt{e}^{(k_{i}+k_{j})x+(k_{i}^{2}+k_{j}^{2})t}]}{(1-\sum_{i=1}^{N}\mathtt{e}^{k_{i}x+k_{i}^{2}t})^{2}},\\ u(x,t) = -\frac{2\sum_{i=1}^{N}k_{i}\mathtt{e}^{k_{i}x+k_{i}^{2}t}}{1-\sum_{i=1}^{N}\mathtt {e}^{k_{i}x+k_{i}^{2}t}}. \end{array} \right . \end{aligned}$$
(53)

5 Conclusions

The Hirota bilinear method is applied to emphasize the integrability of the variant Boussinesq equations. Multiple soliton solutions and multiple singular soliton solutions are formally derived. The analysis confirms the fact that the variant Boussinesq equations have N soliton solutions, and have N singular soliton solutions simultaneously. The results obtained for the phase shift \(a_{ij}\) show that the system is resonance free. The method used here is standard and direct, so we believe that multiple soliton solutions and multiple singular soliton solutions may exist for other classes of nonlinear mathematic physics models, such as the coupled Kadomtsev-Petviashvili system, the Davey-Stewartson system, the generalized Hirota-Satsuma coupled KdV system, and so on. Further work on these aspects is worthy of performing.