Numerical solution of a singularly perturbed Volterra integro-differential equation

Abstract

We study the convergence properties of a difference scheme for singularly perturbed Volterra integro-differential equations on a graded mesh. We show that the scheme is first-order convergent in the discrete maximum norm, independently of the perturbation parameter. Numerical experiments are presented, which are in agreement with the theoretical results.

MSC:45J05, 65R20, 65L11.

1 Introduction

Singularly perturbed Volterra integro-differential equations arise in many physical and biological problems. Among these are diffusion-dissipation processes, epidemic dynamics, synchronous control systems, and filament stretching problems (see, e.g., [1–4]). For extensive reviews, see [1, 3–8].

Singularly perturbed differential equations are typically characterized by a small parameter ε multiplying some or all of the highest-order terms in the differential equations. The difficulties arising in the numerical solutions of singularly perturbed problems are well known. A comprehensive review of the literature on numerical methods for singularly perturbed differential equations may be found in [8–12].

This paper is concerned with the following singularly perturbed Volterra integro-differential equation:

$$Lu:=\epsilon u^{\prime }(t)+f(t,u(t))+{\int }_0^{t}K(t,s,u(s))ds=0,t\in I:=[0,T],$$

(1.1)

$$u(0)=A,$$

(1.2)

where $0<\epsilon \ll 1$ is the perturbation parameter, $f(t,u)$ ($(t,u)\in I\times \mathbb{R}$) and $K(t,s,u)$ ($(t,s,u)\in I\times I\times \mathbb{R}$) are sufficiently smooth functions, A is a given constant and $\frac{\partial f}{\partial u}\ge \alpha >0$. By substituting $\epsilon =0$ in (1.1), we obtain the reduced equation

$$f(t,u_r(t))+{\int }_0^{t}K(t,s,u_r(s))ds=0,$$

which is a Volterra integral equation of the second kind. The singularly perturbed nature of (1.1) occurs when the properties of the solution with $\epsilon >0$ are incompatible with those when $\epsilon =0$. The interest here is in those problems which do imply such an incompatibility in the behavior of u in a neighborhood of $t=0$. This suggests the existence of an initial layer near the origin where the solution undergoes a rapid transition.

A special class of singularly perturbed integro-differential-algebraic equations and singularly perturbed integro-differential systems has been solved by Kauthen [13, 14] by implicit Runge-Kutta methods. A survey of the existing literature on a singularly perturbed Volterra integral and integro-differential equations is given by Kauthen [15]. The exponential scheme that has a fourth-order accuracy when the perturbation parameter ε is fixed is derived and a stability analysis of this scheme is discussed in [16]. The numerical discretization of singularly perturbed Volterra integro-differential equations and Volterra integral equations by tension spline collocation methods in certain tension spline spaces are considered in [17]. For the numerical solution of singularly perturbed Volterra integro-differential equations, we have studied the following articles: [18–21].

Our goal is to construct an ε-numerical method for solving (1.1)-(1.2), by which we mean a numerical method which generates ε-uniformly convergent numerical approximations to the solution. For this, we use a finite difference scheme on an appropriate graded mesh which are dense in the initial layer. Graded meshes are dependent on ε and mesh points have to be condensed in a neighborhood of $t=0$ in order to resolve the initial layer. In graded meshes, basically half of the mesh points are concentrated in a $O(\epsilon |ln\epsilon |)$ neighborhood of the point $t=0$ and the remaining half forms a uniform mesh on the rest of $[0,T]$ (see [10, 11, 22]).

In [23], the authors gave a uniformly convergent numerical method with respect to ε on a uniform mesh for the numerical solution of a linear singularly perturbed Volterra integro-differential equation. However, in this study, we will derive a uniformly convergent ε-numerical method on a graded mesh for the numerical solution of a nonlinear singularly perturbed Volterra integro-differential equation. This is the aspect of the problem of this paper that is different from [23] and the others.

The outline of the paper is as follows: In Section 2, the properties of the problem (1.1), (1.2) are given. In Section 3, the difference scheme constructed on the non-uniform mesh for the numerical solution (1.1), (1.2) is presented and graded mesh is introduced. Stability and convergence of the difference scheme are investigated in Section 4 and error of the difference scheme is evaluated in Section 5. Finally numerical results are presented in Section 6.

Let us now introduce some notation. Let

$${\omega }_N=\{0<t_1<t_2<\cdots <t_{N-1}<t_N=T\},{\varpi }_N={\omega }_N\cup \{t=0\},$$

be the non-uniform mesh on $[0,T]$. For each $i\ge 1$ we set the step size $h_i=t_i-t_{i-1}$.

Here and throughout the paper we use the notation

$$v_{\overline{t},i}=\frac{v_i-v_{i-1}}{h_i},$$

$v_i=v(t_i)$, for any continuous function $v(t)$.

In our estimates, we use the maximum norm given by

$${\parallel v\parallel }_{\mathrm{\infty }}=\underset{[0,T]}{max}|v(t)|.$$

For any discrete function $v_i$, we also define the corresponding discrete norm by

$${\parallel v\parallel }_{\mathrm{\infty },{\omega }_h}\equiv {\parallel v\parallel }_{\mathrm{\infty }}=\underset{1\le i\le N}{max}|v_i|.$$

Throughout the paper, C will denote a generic positive constant that is independent of ε and the mesh parameter.

2 The continuous problem

In this section, we study the behavior of the solution of (1.1)-(1.2) and its first derivative which are required for the analysis of the remainder term in the next sections when the error of the difference scheme is analyzed.

Lemma 2.1 Suppose that $f(t,u)$ and $K(t,s,u)$ have continuous partial derivatives with respect to u, respectively, on $I\times \mathbb{R}$ and $I\times I\times \mathbb{R}$ and have uniformly bounded first partial derivatives in ε. Then the solution $u(x)$ of problem (1.1)-(1.2) satisfies the inequalities

$${\parallel u\parallel }_{\mathrm{\infty }}\le C,$$

(2.1)

$$|u^{\prime }(t)|\le C(1+\frac{1}{\epsilon }exp(-\frac{\alpha t}{\epsilon })),t\in I.$$

(2.2)

Proof The analysis of the convergence properties of numerical method that will be obtained and the study of the behavior of the solution of (1.1)-(1.2) with its first derivative will necessarily involve the linearization of the given problem using the mean value theorem for several variables (see [24]). Hence, we obtain

$$\epsilon u^{\prime }(t)+p(t)u(t)+{\int }_0^{t}G(t,s)u(s)ds=q(t),t\in I,u(0)=A,$$

(2.3)

where

$$\begin{array}{c}p(t)=\frac{\partial }{\partial u}f(t,\theta u),0<\theta <1,\hfill \\ G(t,s)=\frac{\partial }{\partial u}K(t,s,\gamma u),0<\gamma <1\hfill \end{array}$$

and

$$q(t)=-f(t,0)-{\int }_0^{t}K(t,s,0)ds.$$

We show the validity of (2.1). For the solution of the problem (2.3), we have

$$\begin{array}{rl}u(t)=& u(0)exp(-\frac{1}{\epsilon }{\int }_0^{t}p(\eta )d\eta )+\frac{1}{\epsilon }{\int }_0^{t}q(\xi )exp(-\frac{1}{\epsilon }{\int }_{\xi }^{t}q(\eta )d\eta )d\xi \\ -\frac{1}{\epsilon }{\int }_0^t[{\int }_0^{\xi }G(\xi ,s)u(s)ds]exp(-\frac{1}{\epsilon }{\int }_{\xi }^{t}q(\eta )d\eta )d\xi \end{array}$$

and from this we can write

$$\begin{array}{rcl}|u(t)|& \le & |u(0)|exp(-\frac{1}{\epsilon }{\int }_0^{t}p(\eta )d\eta )\\ +\frac{1}{\epsilon }{\int }_0^t|q(\xi )|exp(-\frac{1}{\epsilon }{\int }_{\xi }^{t}p(\eta )d\eta )d\xi \\ +\frac{1}{\epsilon }{\int }_0^t\left[{\int }_0^{\xi }\right|G(\xi ,s)\left|\right|u(s)\left|ds\right]exp(-\frac{1}{\epsilon }{\int }_{\xi }^{t}q(\eta )d\eta )d\xi .\end{array}$$

If $M={max}_{I\times I}|G(t,s)|$, then it follows that

$$\begin{array}{rcl}|u(t)|& \le & |A|exp(-\frac{\alpha t}{\epsilon })+{\alpha }^{-1}{\parallel q\parallel }_{\mathrm{\infty }}(1-exp(-\frac{\alpha t}{\epsilon }))\\ +\frac{1}{\epsilon }M{\int }_0^t\left[{\int }_0^{\xi }\right|u(s)\left|ds\right]exp(-\frac{\alpha (t-\xi )}{\epsilon })d\xi \\ \le & |A|exp(-\frac{\alpha t}{\epsilon })+{\alpha }^{-1}{\parallel q\parallel }_{\mathrm{\infty }}(1-exp(-\frac{\alpha t}{\epsilon }))\\ +M{\alpha }^{-1}(1-exp(-\frac{\alpha t}{\epsilon })){\int }_0^t|u(s)|ds\\ \le & |A|+{\alpha }^{-1}{\parallel q\parallel }_{\mathrm{\infty }}+{\alpha }^{-1}M{\int }_0^t|u(s)|ds.\end{array}$$

Then, applying the Gronwall inequality to the last estimate, we obtain

$$|u(t)|\le (|A|+{\alpha }^{-1}{\parallel q\parallel }_{\mathrm{\infty }})exp\left({\alpha }^{-1}Mt\right),$$

which proves (2.1).

To prove (2.2), differentiating equation (1.1) we have

$$\epsilon v^{\prime }(t)+b(t)v(t)=c(t),$$

(2.4)

where

$$u^{\prime }(t)=v(t),b(t)=\frac{\partial }{\partial u}f(t,u)$$

and

$$c(t)=-\frac{\partial }{\partial u}f(t,u(t))-K(t,t,u(t))-{\int }_0^t\frac{\partial }{\partial t}K(t,s,u(s))ds.$$

By using (1.1), we can obtain

$$|v(0)|=|u^{\prime }(0)|\le {\epsilon }^{-1}|f(0,A)|\le C{\epsilon }^{-1}.$$

(2.5)

It follows from (2.4) that

$$v(t)=v(0)exp(-\frac{1}{\epsilon }{\int }_0^{t}b(\eta )d\eta )+\frac{1}{\epsilon }{\int }_0^{t}c(\xi )exp(-\frac{1}{\epsilon }{\int }_{\xi }^{t}b(\eta )d\eta )d\xi .$$

(2.6)

Obviously, if $f(t,u)$ and $K(t,s,u)$ has continuous partial derivatives in u, respectively, on $I\times \mathbb{R}$ and $I\times I\times \mathbb{R}$, then

$$\frac{1}{\epsilon }|{\int }_0^{t}c(\xi )exp(-\frac{1}{\epsilon }{\int }_{\xi }^{t}b(\eta )d\eta )d\xi |\le C.$$

Hence, we can conclude that (2.2) is a direct consequence of (2.5), (2.6). □

3 Discretization and mesh

To obtain an approximation for (1.1), we integrate (1.1) over $(t_{i-1},t_i)$:

$$h_i^{-1}{\int }_{t_{i-1}}^{t_i}Ludt=0.$$

(3.1)

Using the quadrature rules in [25], we have

$$\epsilon u_{\overline{t},i}+f(t_i,u_i)+{\int }_0^{t_i}K(t_i,s,u(s))ds+R_i^{(1)}+R_i^{(2)}=0,$$

(3.2)

where

$$R_i^{(1)}=-h_i^{-1}{\int }_{t_{i-1}}^{t_i}(\xi -t_{i-1})\frac{d}{d\xi }f(\xi ,u(\xi ))d\xi$$

and

$$R_i^{(2)}=-h_i^{-1}{\int }_{t_{i-1}}^{t_i}(\xi -t_{i-1})\frac{d}{d\xi }\left({\int }_0^{\xi }K(\xi ,s,u(s))ds\right)d\xi .$$

Applying also (2.1) in [25] for $\sigma =\frac{1}{2}$ to the integral in (3.2), we obtain

$${\int }_0^{t_i}K(t_i,s,u(s))ds=\sum _{m=1}^i\frac{h_i}{2}[K(t_i,t_m,u_m)+K(t_i,t_{m-1},u_{m-1})]+R_i^{(3)},$$

(3.3)

where

$$R_i^{(3)}=\sum _{m=1}^i{\int }_{t_{i-1}}^{t_i}(t_{m-\frac{1}{2}}-\xi )\frac{d}{d\xi }K(t_i,\xi ,u(\xi ))d\xi .$$

It is clear from (3.1) and (3.2) that

$$\epsilon u_{\overline{t},i}+f(t_i,u_i)+\sum _{m=1}^i\frac{h_i}{2}[K(t_i,t_m,u_m)+K(t_i,t_{m-1},u_{m-1})]+R_i=0,i=1,\dots ,N,$$

(3.4)

$$u_0=A,$$

(3.5)

where the remainder term is

$$\begin{array}{rcl}{R}_i& =& -h_i^{-1}{\int }_{t_{i-1}}^{t_i}(\xi -t_{i-1})\frac{d}{d\xi }f(\xi ,u(\xi ))d\xi -h_i^{-1}{\int }_{t_{i-1}}^{t_i}(\xi -t_{i-1})\frac{d}{d\xi }\left({\int }_0^{\xi }K(\xi ,s,u(s))ds\right)d\xi \\ +\sum _{m=1}^i{\int }_{t_{i-1}}^{t_i}(t_{m-\frac{1}{2}}-\xi )\frac{d}{d\xi }K(t_i,\xi ,u(\xi ))d\xi .\end{array}$$

(3.6)

Neglecting $R_i$ in (3.3), we may suggest the following difference scheme for approximating (1.1), (1.2):

$$\begin{array}{c}{L}^h{U}_i\equiv \epsilon U_{\overline{t},i}+f(t_i,U_i)+\sum _{m=1}^i\frac{h_i}{2}[K(t_i,t_m,U_m)+K(t_i,t_{m-1},U_{m-1})]\hfill \\ \phantom{L^h{U}_i}=0,i=1,\dots ,N,\hfill \end{array}$$

(3.7)

$$U_0=A.$$

(3.8)

For the difference scheme (3.7), (3.8) to be ε-uniform convergent, we will use a mesh that is graded inside the initial layer region. For an even number N, the graded mesh takes $N/2+1$ points in the interval $[0,\tau ]$ and also $N/2+1$ points in the interval $[\tau ,T]$, where the transition point τ, which separates the fine and coarse portions of the mesh, is obtained by taking

$$\tau =min\{T/2,{\alpha }^{-1}\epsilon |ln\epsilon |\}.$$

(3.9)

In practice one usually has $\tau \ll T$, so the mesh is fine on $[0,\tau ]$ and coarse on $[\tau ,T]$. We shall consider a mesh ${\omega }_N$ which is equidistant in $[\tau ,T]$ but graded in $[0,\tau ]$ by a logarithmic mesh generating function (see [26, 27]). The corresponding mesh points are as follows:

$$\text{if }\tau <T/2,t_i=\{\begin{array}{ll}-{\alpha }^{-1}\epsilon ln[1-(1-\epsilon )2i/N],& i=0,\dots ,N/2,\\ \tau +(i-N/2)h,& i=N/2+1,\dots ,N\end{array}$$

(3.10)

and

$$\text{if }\tau =T/2,t_i=\{\begin{array}{ll}-{\alpha }^{-1}\epsilon ln[1-(1-exp(-\frac{\alpha T}{2\epsilon }))2i/N],& i=0,\dots ,N/2,\\ \tau +(i-N/2)h,& i=N/2+1,\dots ,N,\end{array}$$

(3.11)

where $h=2(T-\tau )/N$.

We only consider the graded mesh defined by (3.9)-(3.11) in the remainder of the paper.

4 Stability and convergence of the difference scheme

Lemma 4.1 Let the difference operator

$$\ell U_i\equiv A_i{U}_i-B_i{U}_{i-1},1\le i\le N,$$

(4.1)

be given, where $A_i>0$ and $B_i>0$. Then we have the following:

• (i) For the difference operator (4.1), the discrete maximum principle holds: If $\ell U_i\ge 0$, $i\ge 1$ and $U_0\ge 0$, then $U_i\ge 0$, $i\ge 0$.

• (ii) If $A_i-B_i\ge \alpha >0$, then the solution of the difference initial value problem

  $$\begin{array}{c}\ell U_i=F_i,i\ge 1,\hfill \\ U_0=\mu \hfill \end{array}$$

satisfies the estimate

$${\parallel U\parallel }_{\mathrm{\infty }}\le |\mu |+{\alpha }^{-1}\underset{1\le i\le N}{max}|F_i|.$$

(4.2)

• (iii) If $F_i\ge 0$ is nondecreasing and $A_i-B_i\ge \alpha >0$, then

  $$|U_i|\le |\mu |+{\alpha }^{-1}{F}_i,i\ge 1.$$

  (4.3)

Proof See [23]. □

Lemma 4.2 Under condition

$$\alpha +\frac{h_i}{2}\frac{\partial }{\partial U}K(t_i,t_i,\gamma U_i)\ge {\alpha }_{\ast }>0,i=1,2,\dots ,N,$$

(4.4)

for the difference operator

$${\ell }^h{U}_i:=\epsilon U_{\overline{t},i}+\frac{\partial }{\partial U}f(t_i,\gamma U_i)U_i+\frac{h_i}{2}\frac{\partial }{\partial U}K(t_i,t_i,\gamma U_i)U_i$$

(4.5)

we have

$${\parallel U\parallel }_{\mathrm{\infty }}\le |U_0|+{\alpha }_{\ast }^{-1}\underset{1\le i\le N}{max}\left|{\ell }^h{U}_i\right|.$$

(4.6)

Proof Difference expression (4.5) can be rewritten as

$$\ell U_i\equiv A_i{U}_i-B_i{U}_{i-1},$$

where

$$A_i=\frac{\epsilon }{h_i}+\frac{\partial }{\partial U}f(t_i,\gamma U_i)+\frac{h_i}{2}\frac{\partial }{\partial U}K(t_i,t_i,\gamma U_i),B_i=\frac{\epsilon }{h_i}.$$

It is easy to see that

$$A_i\ge \frac{\epsilon }{h_i}+\alpha +\frac{h_i}{2}\frac{\partial }{\partial U}K(t_i,t_i,\gamma U_i)>0$$

and

$$B_i=\frac{\epsilon }{h_i}>0.$$

Since

$$A_i-B_i=\frac{\partial }{\partial U}f(t_i,\gamma U_i)+\frac{h_i}{2}\frac{\partial }{\partial U}K(t_i,t_i,\gamma U_i)>0$$

by (4.3), (4.6) follows in view of (4.2). □

Now we will show stability for the difference problem (3.7)-(3.8).

Lemma 4.3 Let the difference operator ${\ell }^h{U}_i$ be defined by (4.5). Then for the difference problem (3.7)-(3.8) we have

$$\left|{\ell }^h{U}_i\right|\le {\parallel f\parallel }_{\mathrm{\infty }}+C\sum _{m=1}^i{h}_i|U_{m-1}|,1\le i\le N.$$

(4.7)

Proof From (3.7) we have

$$\begin{array}{rcl}\left|{\ell }^h{U}_i\right|& \le & |f(t_i,0)|+|\sum _{m=1}^i\frac{h_i}{2}K(t_i,t_m,0)|+\left|\sum _{m=1}^{i-1}\frac{h_i}{2}[\frac{\partial }{\partial U}K(t_i,t_m,\gamma U_m)U_m]\right|\\ +\left|\sum _{m=1}^i\frac{h_i}{2}[K(t_i,t_{m-1},0)+\frac{\partial }{\partial U}K(t_i,t_{m-1},\gamma U_{m-1})U_{m-1}]\right|.\end{array}$$

If we take into consideration that the kernel $K(t,s,u)$ is bounded, it can be concluded that the estimate (4.7) holds. □

Lemma 4.4 We assume that the condition (4.4) holds. Then for the solution of difference scheme (3.7)-(3.8), we have

$$|U_i|\le ({\alpha }_{\ast }^{-1}{\parallel f\parallel }_{\mathrm{\infty }}+|A|)exp\left({\alpha }_{\ast }^{-1}C{t}_i\right),1\le i\le N.$$

(4.8)

Proof Let

$$V_i=\{\begin{array}{ll}{\sum }_{m=1}^{i-1}{h}_i|U_{m-1}|,& i\ge 0,\\ 0,& i=0,\end{array}$$

where

$$V_{\overline{t},i}=|U_{i-1}|.$$

Thus, from the inequality (4.7), we have the following difference inequality:

$$\begin{array}{c}\left|{\ell }^h{U}_i\right|\le C{V}_i+{\parallel f\parallel }_{\mathrm{\infty }},\hfill \\ U_0=A.\hfill \end{array}$$

Using the discrete maximum principle, we have

$$|U_i|\le W_i,$$

where $w_i$ is the solution of the problem

$$\begin{array}{c}{\ell }^h{W}_i=C{V}_i+{\parallel f\parallel }_{\mathrm{\infty }},\hfill \\ W_0=|A|.\hfill \end{array}$$

In view of (4.2), it follows that

$$|U_i|\le |W_i|\le {\alpha }_{\ast }^{-1}C{V}_i+{\alpha }_{\ast }^{-1}{\parallel f\parallel }_{\mathrm{\infty }}+|A|$$

(4.9)

and

$$V_{\overline{t},i}=|U_{i-1}|\le {\alpha }_{\ast }^{-1}C{V}_{i-1}+{\alpha }_{\ast }^{-1}{\parallel f\parallel }_{\mathrm{\infty }}+|A|.$$

Then application of the difference analog of the differential inequality gives

$$V_i\le ({\alpha }_{\ast }^{-1}{\parallel f\parallel }_{\mathrm{\infty }}+|A|){\alpha }_{\ast }{C}^{-1}(exp\left({\alpha }_{\ast }^{-1}C{t}_i\right)-1),$$

which together with (4.9) proves (4.8). □

5 Uniform error estimates

To investigate the convergence of the method, note that the error function $z_i=U_i-u_i$, $0\le i\le N$, is the solution of the discrete problem

$$\begin{array}{c}{L}^h{z}_i=\epsilon z_{\overline{t},i}+[f(t_i,U_i)-f(t_i,u_i)]+\frac{h_i}{2}[K(t_i,t_i,U_i)-K(t_i,t_i,u_i)]\hfill \\ \phantom{L^h{z}_i=}+\frac{h_i}{2}[K(t_i,t_{i-1},U_{i-1})-K(t_i,t_{i-1},u_{i-1})]\hfill \\ \phantom{L^h{z}_i=}+{\tilde{K}}_i=R_i,i=1,\dots ,N,\hfill \end{array}$$

(5.1)

$$z_0=0,$$

(5.2)

where $R_i$ is given by (3.6) and

$${\tilde{K}}_i=\{\begin{array}{ll}0,& i=1,\\ {\sum }_{m=1}^{i-1}\frac{h_i}{2}\{[K(t_i,t_m,U_m)-K(t_i,t_m,u_m)]\\ +[K(t_i,t_{m-1},U_{m-1})-K(t_i,t_{m-1},u_{m-1})]\},& i>1.\end{array}$$

Lemma 5.1 Under the condition of Lemma  2.1, for the remainder term $R_i$ of the scheme (3.7)-(3.8), the estimate

$${\parallel R\parallel }_{\mathrm{\infty },{\omega }_N}\le C{N}^{-1}$$

(5.3)

holds.

Proof The remainder term of the scheme (3.7) can be rewritten as

$$R_i=R_i^{(1)}+R_i^{(2)}+R_i^{(3)},$$

where

$$R_i^{(1)}=-h_i^{-1}{\int }_{t_{i-1}}^{t_i}(\xi -t_{i-1})\frac{d}{d\xi }f(\xi ,u(\xi ))d\xi ,$$

(5.4)

$$R_i^{(2)}=-h_i^{-1}{\int }_{t_{i-1}}^{t_i}(\xi -t_{i-1})\frac{d}{d\xi }\left({\int }_0^{\xi }K(\xi ,s,u(s))ds\right)d\xi$$

(5.5)

and

$$R_i^{(3)}=\sum _{m=1}^i{\int }_{t_{i-1}}^{t_i}(t_{m-\frac{1}{2}}-\xi )\frac{d}{d\xi }K(t_i,\xi ,u(\xi ))d\xi .$$

(5.6)

In view of Lemma 2.1, for an arbitrary mesh, it follows from (5.4), (5.5), and (5.6) that

$$\begin{array}{c}\left|R_i^{(1)}\right|\le h_i^{-1}{\int }_{t_{i-1}}^{t_i}(\xi -t_{i-1})\left|\frac{d}{d\xi }f(\xi ,u(\xi ))\right|d\xi \hfill \\ \phantom{|R_i^{(1)}|}=h_i^{-1}{\int }_{t_{i-1}}^{t_i}(\xi -t_{i-1})|\frac{\partial }{\partial \xi }f(\xi ,u(\xi ))+\frac{\partial }{\partial u}f(\xi ,u(\xi ))u^{\prime }(\xi )|d\xi \hfill \\ \phantom{|R_i^{(1)}|}\le C{h}_i^{-1}{\int }_{t_{i-1}}^{t_i}(\xi -t_{i-1})|1+u^{\prime }(\xi )|d\xi \hfill \\ \phantom{|R_i^{(1)}|}\le C\{h_i+{\epsilon }^{-1}{\int }_{t_{i-1}}^{t_i}|u^{\prime }(\xi )\left|d\xi \right\},i=1,\dots ,N,\hfill \end{array}$$

(5.7)

$$\begin{array}{c}\left|R_i^{(2)}\right|\le h_i^{-1}{\int }_{t_{i-1}}^{t_i}|(\xi -t_{i-1})\frac{d}{d\xi }\left({\int }_0^{\xi }K(\xi ,s,u(s))ds\right)|d\xi \hfill \\ \phantom{|R_i^{(2)}|}\le h_i^{-1}{\int }_{t_{i-1}}^{t_i}(\xi -t_{i-1})|K(\xi ,\xi ,u(\xi ))+{\int }_0^{\xi }\frac{\partial }{\partial \xi }K(\xi ,s,u(s))ds|d\xi \hfill \\ \phantom{|R_i^{(2)}|}\le C{h}_i,i=1,\dots ,N,\hfill \end{array}$$

(5.8)

$$\begin{array}{c}\left|R_i^{(3)}\right|\le \sum _{m=1}^i{\int }_{t_{i-1}}^{t_i}(t_{m-\frac{1}{2}}-\xi )\left|\frac{d}{d\xi }K(t_i,\xi ,u(\xi ))\right|d\xi \hfill \\ \phantom{|R_i^{(3)}|}\le \sum _{m=1}^i{\int }_{t_{i-1}}^{t_i}(t_{m-\frac{1}{2}}-\xi )|\frac{\partial }{\partial \xi }K(t_i,\xi ,u(\xi ))+\frac{\partial }{\partial u}K(t_i,\xi ,u(\xi ))u^{\prime }(\xi )|d\xi \hfill \\ \phantom{|R_i^{(3)}|}\le \sum _{m=1}^i{\int }_{t_{i-1}}^{t_i}(t_{m-\frac{1}{2}}-\xi )|1+u^{\prime }(\xi )|d\xi \hfill \\ \phantom{|R_i^{(3)}|}\le C\underset{1\le m\le i}{max}{h}_m{\int }_0^{t_i}(1+u^{\prime }(\xi ))d\xi \hfill \\ \phantom{|R_i^{(3)}|}\le C\underset{1\le m\le i}{max}{h}_m,i=1,2,\dots ,N,\hfill \end{array}$$

(5.9)

respectively, where

$$h_i=\{\begin{array}{ll}-{\alpha }^{-1}\epsilon ln[1-(1-\epsilon )\frac{2i}{N}]+{\alpha }^{-1}\epsilon ln[1-(1-\epsilon )\frac{2(i-1)}{N}],& i=1,\dots ,N/2,\\ \frac{T-\tau }{N/2},& i=N/2+1,\dots ,N.\end{array}$$

First, we consider the $\tau <T/2$ and estimate $R_i$ on $[0,\tau ]$ and $[\tau ,T]$ separately. Then $\tau =-{\alpha }^{-1}\epsilon ln\epsilon$. In the layer region $[0,\tau ]$, we get

$$\left|R_i^{(1)}\right|\le C\{h_i+{\alpha }^{-1}(exp(-\frac{\alpha t_{i-1}}{\epsilon })+exp(-\frac{\alpha t_i}{\epsilon }))\},i=1,\dots ,N/2,$$

(5.10)

by (2.2). Since

$$\begin{array}{rcl}{h}_i& =& t_i-t_{i-1}=-{\alpha }^{-1}\epsilon ln[1-(1-\epsilon )\frac{2i}{N}]+{\alpha }^{-1}\epsilon ln[1-(1-\epsilon )\frac{2(i-1)}{N}]\\ \le & 2{\alpha }^{-1}(1-\epsilon )N^{-1}\end{array}$$

and

$$exp(-\frac{\alpha t_{i-1}}{\epsilon })+exp(-\frac{\alpha t_i}{\epsilon })=2(1-\epsilon )N^{-1},$$

it follows from (5.10) that

$$\left|R_i^{(1)}\right|\le 4{\alpha }^{-1}C{N}^{-1},i=1,\dots ,N/2.$$

(5.11)

It follows from (5.8) and (5.9) that

$$\left|R_i^{(2)}\right|\le Ch\le C2{\alpha }^{-1}(1-\epsilon )N^{-1}\le 2{\alpha }^{-1}C{N}^{-1},i=1,\dots ,N/2$$

(5.12)

and

$$\left|R_i^{(3)}\right|\le C{h}_i+C{\epsilon }^{-1}{h}_i\le C{N}^{-1},i=1,\dots ,N/2,$$

(5.13)

respectively. From (5.11), (5.12), and (5.13) for the region $[0,\tau ]$ we get

$$|R_i|\le C{N}^{-1},i=1,\dots ,N/2.$$

(5.14)

In the layer region $[\tau ,T]$, $|u^{\prime }(x)|\le C$ (or ${\epsilon }^{-1}exp(-\alpha x/\epsilon )\le 1$) by (2.2), and

$$\left|R_i^{(1)}\right|\le Ch,i=N/2+1,\dots ,N.$$

In view of the above discussion, we get

$$\left|R_i^{(1)}\right|\le 2TC{N}^{-1},i=N/2+1,\dots ,N.$$

(5.15)

Similarly, it is clear that

$$\left|R_i^{(2)}\right|\le 2TC{N}^{-1},i=N/2+1,\dots ,N$$

(5.16)

and

$$\left|R_i^{(3)}\right|\le 2TC{N}^{-1},i=N/2+1,\dots ,N.$$

(5.17)

Combining the estimates (5.11), (5.12), and (5.13) for the region $[\tau ,T]$, we get

$$|R_i|\le C{N}^{-1},i=N/2+1,\dots ,N.$$

(5.18)

Now we consider the case $\tau =T/2$. In this case, $T/2<-{\alpha }^{-1}\epsilon ln\epsilon$. Therefore, for $t_i\in [0,\tau ]$ with (3.10), we can obtain similar results to that obtained above. For $t_i\in (\tau ,T]$, since $h_i=h=2(T-\tau )/N=T/N$,

$$\begin{array}{rl}\underset{i=N/2+1,\dots ,N}{max}{\int }_{t_{i-1}}^{t_i}{\epsilon }^{-1}exp(-\frac{\alpha t}{\epsilon })dx& \le h{\epsilon }^{-1}exp(-\frac{\alpha T}{2\epsilon })\\ \le (2{\alpha }^{-1}exp(-1)h)/T=2C{\alpha }^{-1}exp(-1)N^{-1}.\end{array}$$

It follows from (5.7), (5.8), and (5.9) that

$$\left|R_i^{(1)}\right|\le C(T+2exp(-1){\alpha }^{-1})N^{-1},i=N/2+1,\dots ,N,$$

(5.19)

$$\left|R_i^{(2)}\right|\le Ch\le C{N}^{-1},i=N/2+1,\dots ,N,$$

(5.20)

$$\left|R_i^{(3)}\right|\le Ch+C{\epsilon }^{-1}h\le C{N}^{-1},i=N/2+1,\dots ,N,$$

(5.21)

respectively. When we combine the estimates (5.19), (5.20), and (5.21), we get

$$|R_i|\le C{N}^{-1},i=N/2+1,\dots ,N.$$

(5.22)

From (5.14), (5.18), and (5.22), it is easy to see that (5.3) holds. □

Lemma 5.2 Under condition (4.4) and Lemma  5.1, the solution $z_i$ of problem (5.1)-(5.2) satisfies

$${\parallel z\parallel }_{\mathrm{\infty },{\varpi }_N}\le \underset{1\le i\le N}{max}|R_i|.$$

(5.23)

Proof Using intermediate value theorem for the problem (3.7)-(3.8), we get

$$\begin{array}{c}{L}^h{z}_i=\epsilon z_{\overline{t},i}+\frac{\partial }{\partial u}f(t_i,u_i+\gamma z_i)z_i+\frac{h_i}{2}\frac{\partial }{\partial u}K(t_i,t_i,u_i+\gamma z_i)z_i\hfill \\ \phantom{L^h{z}_i=}+\frac{h_i}{2}\frac{\partial }{\partial u}K(t_i,t_{i-1},u_{i-1}+\gamma z_{i-1})z_{i-1}+\tilde{K}\hfill \\ \phantom{L^h{z}_i}=R_i,i=1,2,\dots ,N,\hfill \end{array}$$

(5.24)

$$z_0=0,$$

(5.25)

where

$$\tilde{K}=\{\begin{array}{ll}0,& i=1,\\ {\sum }_{m=1}^{i-1}\frac{h_i}{2}[\frac{\partial }{\partial u}K(t_i,t_m,u_m+\gamma z_m)z_m+\frac{\partial }{\partial u}K(t_i,t_{m-1},u_{m-1}+\gamma z_{m-1})z_{m-1}],& i>1.\end{array}$$

If we apply Lemma 4.4 to (5.24)-(5.25), then we see the validity of the inequality (5.23). □

Combining the two previous lemmas gives us the following main result.

Theorem 5.3 Suppose that the conditions of Lemma  5.1 and (4.4) are satisfied and u is the solution of problem (1.1), (1.2). Then the following ε-uniform convergence result holds for the solution U of the difference problem (3.7), (3.8) on the mesh (3.9)-(3.11):

$${\parallel U-u\parallel }_{\mathrm{\infty },{\varpi }_N}\le C{N}^{-1}.$$

6 Numerical results

In this section, we test the performance of the difference problem (3.7), (3.8). It is clear that the difference problem (3.7), (3.8) is a nonlinear problem. When we solve such problems, nonlinear equations arise in each step. There are several methods for solving these kinds of nonlinear equations. One of these methods is quasi-linearization. Quasi-linearization is a method like Newton’s method (see, e.g., [28]). This method amounts to linearizing the nonlinear terms in the nonlinear problems. A quasi-linearization procedure defines a sequence of linear problems whose solutions converge to that of the given nonlinear problems. For convergence of this method, one can refer to [28, 29]. If we use this method for the difference problem (3.7), (3.8), we obtain

$$\begin{array}{c}\epsilon U_{\overline{t},i}^{(n)}+f(t_i,U_i^{(n-1)})+\frac{\partial }{\partial U}f(t_i,U_i^{(n-1)})(U_i^{(n)}-U_i^{(n-1)})\hfill \\ +\sum _{m=1}^i\frac{h_i}{2}[K(t_i,t_m,U_m^{(n-1)})+\frac{\partial }{\partial U}K(t_i,t_m,U_m^{(n-1)})(U_m^{(n)}-U_m^{(n-1)})\hfill \\ +K(t_i,t_{m-1},U_{m-1}^{(n-1)})+\frac{\partial }{\partial U}K(t_i,t_{m-1},U_{m-1}^{(n-1)})(U_{m-1}^{(n)}-U_{m-1}^{(n-1)})]\hfill \\ =0,i=1,\dots ,N,\hfill \end{array}$$

(6.1)

$$U_0^{(n)}=A.$$

(6.2)

Here, we obtain the following iteration process:

$$U_i^{(n)}=\frac{A_i{U}_{i-1}^{(n)}+B_i{U}_i^{(n-1)}-C_i-{\tilde{K}}_i}{\frac{\epsilon }{h_i}+\frac{\partial }{\partial U}f(t_i,U_i^{(n-1)})+\frac{h_i}{2}\frac{\partial }{\partial U}K(t_i,t_i,U_i^{(n-1)})},i=1,2,\dots ,N,$$

(6.3)

$$U_0^{(n)}=A,$$

(6.4)

where

$$\begin{array}{c}{A}_i=\frac{\epsilon }{h_i},B_i=\frac{\partial }{\partial U}f(t_i,U_i^{(n-1)})+\frac{\partial }{\partial U}K(t_i,t_i,U_i^{(n-1)}),\hfill \\ C_i=f(t_i,U_i^{(n-1)})+\frac{h_i}{2}[K(t_i,t_i,U_i^{(n-1)})+K(t_i,t_{i-1},U_{i-1}^{(n)})],\hfill \\ {\tilde{K}}_i=\{\begin{array}{ll}0,& i=1,\\ {\sum }_{m=1}^{i-1}\frac{h_i}{2}[K(t_i,t_m,U_m^{(n)})+K(t_i,t_{m-1},U_{m-1}^{(n)})],& i>1,\end{array}\hfill \end{array}$$

and $U_i^{(0)}$ is given.

We apply the difference scheme (3.7), (3.8) to the following Volterra integro-differential equation:

$$\epsilon u^{\prime }(t)+u^3(t)+3u(t)+{\int }_0^t{u}^2(s)ds=e^{-\frac{3t}{\epsilon }}-\frac{1}{2}\epsilon e^{-\frac{2t}{\epsilon }}+2e^{-\frac{t}{\epsilon }}+\frac{1}{2}\epsilon$$

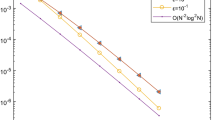
with $u(0)=1$. The exact solution of the equation is $u(t)=e^{-\frac{t}{\epsilon }}$. Some computational results are presented in Table 1. We also calculate the experimental rate of uniform convergence p as follows:

$$p^N=\frac{ln(e^N/e^{2N})}{ln2},$$

where

$$e^N=\underset{1\le i\le N}{max}|U_i-u_i|.$$

The obtained results show that the convergence rate of the difference scheme (3.7), (3.8) is essentially in accord with the theoretical analysis.

Table 1 Approximate errors ${\mathit{e}}^{\mathit{N}}$ and computed orders of convergence ${\mathit{p}}^{\mathit{N}}$ on ${\overline{\mathit{\omega }}}_{\mathit{N}}$ for various values of ε and N

7 Conclusion

A nonlinear Volterra integro-differential equation was considered. We solved this equation by using a finite difference scheme on an appropriate graded mesh which is dense in the initial layer. We showed that the method shows uniform convergence with respect to the perturbation parameter for the numerical approximation of the solution. Numerical results which support the theoretical results were presented.