Extension of the differential transformation method to nonlinear differential and integro-differential equations with proportional delays

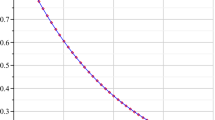
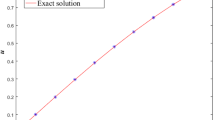
Abstract

In this paper, the differential transformation method is applied by providing new theorems to develop exact and approximate solutions of nonlinear differential and integro-differential equations with proportional delays represented by nonlinear multi-pantograph equations. Some examples are given to demonstrate the validity and applicability of the present method and a comparison is made with existing results.

1 Introduction

In this paper, we consider the following nonlinear differential and integro-differential equations with proportional delays:

$$\begin{array}{c}\mathcal{F}(t,u(p_{0}t),u^{\prime }(p_{1}t),\dots ,u^{(n)}(p_{n}t))=0,t\ge 0,\hfill \\ \mathcal{G}(t,u(p_{0}t),u^{\prime }(p_{1}t),\dots ,u^{(n)}(p_{n}t),{\int }_0^{rt}K(t,s,u(q_{0}s),u^{\prime }(q_{1}s),\dots ,u^{(m)}(q_{m}s))ds)\hfill \\ =0,t\ge 0,\hfill \end{array}$$

where ℱ, , K are given functions with appropriate domains of definition, $p_i,q_j,r\in (0,1)$, $i=0,1,\dots ,n$, $j=0,1,\dots ,m$, $m<n$.

Functional differential and integro-differential equations with proportional delays are usually referred to as pantograph equations or generalized equations, and, as well, they are often used to model some problems with aftereffect in mechanics and the related scientific fields [1–13]. Many typical examples such as stress-strain states of materials, motion of rigid bodies and models of polymer crystallization can be found in Kolmanovskii and Myshkis’s monograph [14] and the references therein.

2 Differential transformation method

The method that is developed in this work depends on the differential transformation method (DTM) introduced by Zhou [15] in a study of electric circuits. This method constructs a semi-analytical numerical technique that uses Taylor series for the solution of differential equations in the form of polynomials. It is different from the high-order Taylor series method which requires symbolic computation of the necessary derivatives of the data functions.

There is no need for linearization or perturbations, large computational work and round-off errors are avoided. It has been used to solve effectively, easily and accurately a large class of linear and nonlinear problems with approximations [16–25].

The differential transformation of the k th derivative of function $u(t)$ is defined as follows:

$$U(k)=\frac{1}{k!}{\left[\frac{d^{k}u(t)}{d{t}^k}\right]}_{t=t_0},$$

(1)

where $u(t)$ is the original function and $U(k)$ is the transformed function. Differential inverse transformation of $U(k)$ is defined as follows:

$$u(t)=\sum _{k=0}^{\mathrm{\infty }}U(k){(t-t_0)}^k.$$

(2)

In fact, inverse transformation (2) implies that the concept of differential transformation is derived from the Taylor series expansion. Although DTM is not able to evaluate the derivatives symbolically, relative derivatives can be calculated in an iterative way which is described by the transformed equations of the original function.

From definitions (1), (2) we can derive the following.

Theorem 1 Assume that $F(k)$, $G(k)$, $H(k)$ and $U_i(k)$, $i=1,\dots ,n$, are the differential transformations of the functions $f(t)$, $g(t)$, $h(t)$ and $u_i(t)$, $i=1,\dots ,n$, respectively, then:

$$\begin{array}{c}\mathit{\text{If}}f(t)=\frac{d^{n}g(t)}{d{t}^n},\mathit{\text{then}}F(k)=\frac{(k+n)!}{k!}G(k+n).\hfill \\ \mathit{\text{If}}f(t)=g(t)h(t),\mathit{\text{then}}F(k)=\sum _{l=0}^{k}G(l)H(k-l).\hfill \\ \mathit{\text{If}}f(t)=t^n,\mathit{\text{then}}F(k)=\delta (k-n),\delta \mathit{\text{is the Kronecker delta symbol}}.\hfill \\ \mathit{\text{If}}f(t)=e^{\lambda t},\mathit{\text{then}}F(k)=\frac{{\lambda }^k}{k!}.\hfill \\ \mathit{\text{If}}f(t)=g(t){\int }_0^{t}h(s)ds,\mathit{\text{then}}F(k)=\frac{G(k-1)}{k},\mathit{\text{where}}k\ge 1.\hfill \\ \mathit{\text{If}}f(t)=\prod _{i=1}^n{u}_i(t),\mathit{\text{then}}\hfill \\ F(k)=\sum _{r_1=0}^k\sum _{r_2=0}^{k-r_1}\cdots \sum _{r_n=0}^{k-r_1-\cdots -r_{n-1}}{U}_1(r_1)\cdots U_{n-1}(r_{n-1})U_n(k-r_1-\cdots -r_n).\hfill \end{array}$$

The proof of Theorem 1 is given in [26].

3 Main results

In this section, we state the fundamental theorems of this paper.

Theorem 2 Assume that $W(k)$, $U(k)$ and $U_i(k)$ are the differential transformations of the functions $w(t)$, $u(t)$ and $u_i(t)$, respectively, and $q,q_i\in (0,1)$, $i=1,2$. Then:

$$\begin{array}{rl}(\mathrm{i})& \mathit{\text{If}}w(t)=u(qt),\mathit{\text{then}}W(k)=q^{k}U(k).\\ (\mathrm{ii})& \mathit{\text{If}}w(t)=u_1(q_{1}t)u_2(q_{2}t),\mathit{\text{then}}W(k)=\sum _{l=0}^k{q}_1^l{q}_2^{k-l}{U}_1(l)U_2(k-l).\\ (\mathrm{iii})& \mathit{\text{If}}w(t)=\frac{d^m}{d{t}^m}u(qt),\mathit{\text{then}}W(k)=\frac{(k+m)!}{k!}{q}^{k+m}U(k+m).\\ (\mathrm{iv})& \mathit{\text{If}}w(t)=\frac{d^n}{d{t}^n}{u}_1(q_{1}t)\frac{d^m}{d{t}^m}{u}_2(q_{2}t),\mathit{\text{then}}\\ W(k)=\sum _{l=0}^k{q}_1^{l+n}{q}_2^{k-l+m}\frac{(l+n)!(k-l+m)!}{l!(k-l)!}{U}_1(l+n)U_2(k-l+m).\end{array}$$

Proof (i) From equation (1), we get

$$\frac{d^k}{d{t}^k}w(t)=\frac{d^k}{d{t}^k}[u(qt)]=q^k\frac{d^k}{d{\tilde{t}}^k}u(\tilde{t}),$$

where $\tilde{t}=qt$, thus

$${[\frac{d^k}{d{t}^k}w(t)]}_{t=t_0}=q^k{[\frac{d^k}{d{\tilde{t}}^k}u(\tilde{t})]}_{t=t_0}=q^{k}k!U(k)$$

and using (1) we have

$$W(k)=\frac{1}{k!}{\left[\frac{d^{k}w(t)}{d{t}^k}\right]}_{t=t_0}=\frac{1}{k!}{q}^{k}k!U(k)=q^{k}U(k),$$

where $k\in \mathbb{N}\cup \{0\}$.

• (ii) Using the Leibnitz formula, we obtain

  $$\begin{array}{rcl}\frac{d^k}{d{t}^k}w(t)& =& \frac{d^k}{d{t}^k}[u_1(q_{1}t)u_2(q_{2}t)]=\sum _{l=0}^k\left(\genfrac{}{}{0ex}{}{k}{l}\right)\frac{d^l}{d{t}^l}[u_1(q_{1}t)]\frac{d^{k-l}}{d{t}^{k-l}}[u_2(q_{2}t)]\\ =& \sum _{l=0}^k\left(\genfrac{}{}{0ex}{}{k}{l}\right)\frac{d^l}{d{\tilde{t}}^l}[u_1(\tilde{t})]\frac{d^{k-l}}{d{\hat{t}}^{k-l}}[u_2(\hat{t})],\end{array}$$

where $\tilde{t}=q_{1}t$, $\hat{t}=q_{2}t$, and hence

$${[\frac{d^k}{d{t}^k}w(t)]}_{t=t_0}=\sum _{l=0}^k\left(\genfrac{}{}{0ex}{}{k}{l}\right)[q_1^{l}l!U_1(l)][q_2^{k-l}(k-l)!U_2(k-l)]=\sum _{l=0}^{k}k!q_1^l{q}_2^{k-l}{U}_1(l)U_2(k-l).$$

From equation (1), we have

$$W(k)=\frac{1}{k!}{[\frac{d^k}{d{t}^k}w(t)]}_{t=t_0}=\sum _{l=0}^{k}k!q_1^l{q}_2^{k-l}{U}_1(l)U_2(k-l),k\in \mathbb{N}\cup \{0\}.$$

• (iii) From the proof of formula (i), we get

  $${[\frac{d^{k+m}}{d{t}^{k+m}}w(t)]}_{t=t_0}=q^{k+m}{[\frac{d^{k+m}}{d{\tilde{t}}^{k+m}}u(\tilde{t})]}_{t=t_0}=(k+m)!q^{k+m}U(k+m).$$

Then

$$W(k)=\frac{1}{k!}{[\frac{d^k}{d{t}^k}w(t)]}_{t=t_0}=\frac{(k+m)!}{k!}{q}^{k+m}U(k+m).$$

• (iv) Analogously, from to previous part of the proof, we get

  $$\begin{array}{rcl}\frac{d^k}{d{t}^k}w(t)& =& \frac{d^k}{d{t}^k}[\frac{d^n}{d{t}^n}{u}_1(q_{1}t)\frac{d^m}{d{t}^m}{u}_2(q_{2}t)]\\ =& \sum _{l=0}^k\left(\genfrac{}{}{0ex}{}{k}{l}\right)\frac{d^l}{d{t}^l}[\frac{d^n}{d{t}^n}{u}_1(q_{1}t)]\frac{d^{k-l}}{d{t}^{k-l}}[\frac{d^m}{d{t}^m}{u}_2(q_{2}t)]\\ =& \sum _{l=0}^k\left(\genfrac{}{}{0ex}{}{k}{l}\right)q_1^{l+n}\frac{d^{l+n}}{d{\tilde{t}}^{l+n}}{u}_1(\tilde{t})q_2^{k-l+m}\frac{d^{k-l+m}}{d{\hat{t}}^{k-l+m}}{u}_2(\hat{t}),\end{array}$$

where $\tilde{t}=q_{1}t$, $\hat{t}=q_{2}t$; therefore

$$\begin{array}{rcl}\frac{d^k}{d{t}^k}w(t)& =& \sum _{l=0}^k\left(\genfrac{}{}{0ex}{}{k}{l}\right)[q_1^{l+n}(l+n)!U_1(l+n)][q_2^{k-l+m}(k-l+m)!U_2(k-l+m)]\\ =& \sum _{l=0}^k\frac{k!(l+n)!(k-l+m)!}{l!(k-l)!}{q}_1^{l+n}{q}_2^{k-l+m}{U}_1(l+n)U_2(k-l+m).\end{array}$$

Then from (1), we have

$$W(k)=\sum _{l=0}^k{q}_1^{l+n}{q}_2^{k-l+m}\frac{(l+n)!(k-l+m)!}{l!(k-l)!}{U}_1(l+n)U_2(k-l+m).$$

The proof is complete. □

Theorem 3 Assume that $W(k)$, $U(k)$ and $U_i(k)$ are the differential transformations of the functions $w(t)$, $u(t)$ and $u_i(t)$, respectively, and $r,q,q_i\in (0,1)$, $i=1,2$. Then:

$$\begin{array}{rl}(\mathrm{I})& \mathit{\text{If}}w(t)={\int }_0^{rt}u(qs)ds,\mathit{\text{then}}W(k)=\frac{1}{k}{r}^k{q}^{k-1}U(k-1).\\ (\mathrm{II})& \mathit{\text{If}}w(t)={\int }_0^{rt}{u}_1(q_{1}s)u_2(q_{2}s)ds,\mathit{\text{then}}W(k)=\frac{1}{k}\sum _{l=0}^{k-1}{r}^k{q}_1^l{q}_2^{k-l-1}{U}_1(l)U_2(k-l-1).\\ (\mathrm{III})& \mathit{\text{If}}w(t)=u(qt){\int }_0^{rt}{u}_1(q_{1}s)u_2(q_{2}s)ds,\mathit{\text{then}}\\ W(k)=\sum _{l=0}^{k-1}\sum _{s=0}^{k-l-1}\frac{1}{k-l}{r}^{k-l}{q}^l{q}_1^s{q}_2^{k-l-s-1}U(l)U_1(s)U_2(k-l-s-1),\end{array}$$

where $k\in \mathbb{N}$.

Proof (I) It is obvious that

$$\frac{d^k}{d{t}^k}w(t)=r\frac{d^{k-1}}{d{t}^{k-1}}u(rqt),$$

then

$${[\frac{d^k}{d{t}^k}w(t)]}_{t=t_0}=r(k-1)!{(rq)}^{k-1}U(k-1)=(k-1)!r^k{q}^{k-1}U(k-1).$$

From here and equation (1), we get

$$W(k)=\frac{1}{k!}{[\frac{d^k}{d{t}^k}w(t)]}_{t=t_0}=\frac{1}{k}{r}^k{q}^{k-1}U(k-1),k\in \mathbb{N}.$$

• (II) Similarly as in previous part (I), we have

  $$\begin{array}{rcl}\frac{d^k}{d{t}^k}w(t)& =& r\frac{d^{k-1}}{d{t}^{k-1}}[u_1(r{q}_{1}t)u_2(r{q}_{2}t)]\\ =& r\sum _{l=0}^{k-1}\left(\genfrac{}{}{0ex}{}{k-1}{l}\right){(r{q}_1)}^l\frac{d^l}{d{\tilde{t}}^l}{u}_1(\tilde{t}){(r{q}_2)}^{k-l-1}\frac{d^{k-l-1}}{d{\hat{t}}^{k-l-1}}{u}_2(\hat{t}),\end{array}$$

where $\tilde{t}=q_{1}t$, $\hat{t}=q_{2}t$. Then

$${[\frac{d^k}{d{t}^k}w(t)]}_{t=t_0}=r\sum _{l=0}^{k-1}\left(\genfrac{}{}{0ex}{}{k-1}{l}\right){(r{q}_1)}^{l}l!U_1(l){(r{q}_2)}^{k-l-1}(k-l-1)!U_2(k-l-1).$$

Using equation (1), we obtain

$$\begin{array}{rcl}W(k)& =& \frac{1}{k!}{[\frac{d^k}{d{t}^k}w(t)]}_{t=t_0}\\ =& \frac{1}{k}\sum _{l=0}^{k-1}{r}^k{q}_1^l{q}_2^{k-l-1}{U}_1(l)U_2(k-l-1),k\in \mathbb{N}.\end{array}$$

• (III) Put $h(t)={\int }_0^{rt}{u}_1(q_{1}s)u_2(q_{2}s)ds$, then from the previous part we get

  $$\frac{d^k}{d{t}^k}w(t)=\frac{d^k}{d{t}^k}[u(qt)h(t)]=\sum _{l=0}^k\left(\genfrac{}{}{0ex}{}{k}{l}\right)p^l\frac{d^l}{d{\tilde{t}}^l}u(\tilde{t})\frac{d^{k-l}}{d{t}^{k-l}}h(t),$$

  (3)

where $\tilde{t}=qt$, and

$$\begin{array}{rcl}\frac{d^{k-l}}{d{t}^{k-l}}h(t)& =& r\frac{d^{k-l-1}}{d{t}^{k-l-1}}[u_1(r{q}_{1}t)u_2(r{q}_{2}t)]\\ =& r\sum _{s=0}^{k-l-1}\left(\genfrac{}{}{0ex}{}{k-l-1}{s}\right){(r{q}_1)}^s\frac{d^s}{d{\tilde{t}}^s}{u}_1(\tilde{t}){(r{q}_2)}^{k-l-s-1}\frac{d^{k-l-s-1}}{d{\hat{t}}^{k-l-s-1}}{u}_2(\hat{t}),\end{array}$$

(4)

where $\tilde{t}=q_{1}t$, $\hat{t}=q_{2}t$. From (3) and (4), we obtain

$$\begin{array}{rcl}{[\frac{d^k}{d{t}^k}w(t)]}_{t=t_0}& =& \sum _{l=0}^k\sum _{s=0}^{k-l-1}\left(\genfrac{}{}{0ex}{}{k}{l}\right)\left(\genfrac{}{}{0ex}{}{k-l-1}{s}\right)r^{k-l}{q}^l{q}_1^s{q}_2^{k-l-s-1}\\ \times l!s!(k-l-s-1)!U(l)U_1(s)U_2(k-l-s-1),\end{array}$$

but for $l=k$ we get ${[\frac{d^{k-l}}{d{t}^{k-l}}y(t)]}_{t=t_0}=0$. Then, using equation (1), we get

$$W(k)=\sum _{l=0}^{k-1}\sum _{s=0}^{k-l-1}\frac{1}{k-l}{r}^{k-l}{q}^l{q}_1^s{q}_2^{k-l-s-1}U(l)U_1(s)U_2(k-l-s-1),k\in \mathbb{N}.$$

The proof is complete. □

Some above mentioned formulae were proved by Abazari and Kilicman [27] or Mirzaee and Lafiti [28] but with many mistakes and in incorrect way, respectively.

4 Numerical examples

Example 1 As a practical example, we consider the following pantograph delay equation:

$$u^{\prime }(t)=\frac{1}{2}exp\frac{t}{2}u\left(\frac{t}{2}\right)+\frac{1}{2}u(t),u(0)=1.$$

(5)

Using the differential transformation method, the differential transform version of equation (5) is

$$(k+1)U(k+1)=\frac{1}{2}\sum _{l=0}^k\frac{1}{2^{l}l!}\frac{1}{2^{k-l}}U(k-l)+\frac{1}{2}U(k),k\ge 0$$

(6)

and the differential transform version of the initial condition $u(0)=1$ has the form $U(0)=1$. From equation (6), we obtain the recurrence system of equations

$$U(k+1)=\frac{1}{2k+2}[\sum _{l=0}^k\frac{1}{2^{k}l!}U(k-l)+U(k)],k\ge 0.$$

(7)

From system (7), we have

$$\begin{array}{c}U(1)=\frac{1}{2}[U(0)+U(0)]=1,\hfill \\ U(2)=\frac{1}{4}[\frac{1}{2}U(1)+\frac{1}{2}U(0)+U(1)]=\frac{1}{2},\hfill \\ U(3)=\frac{1}{6}[\frac{1}{4}U(2)+\frac{1}{4}U(1)+\frac{1}{8}U(0)+U(2)]=\frac{1}{6},\hfill \\ U(4)=\frac{1}{8}[\frac{1}{8}U(3)+\frac{1}{8}U(2)+\frac{1}{16}U(1)+\frac{1}{48}U(0)+U(3)]=\frac{1}{24},\hfill \\ ⋮\hfill \end{array}$$

Using the inverse transformation rule (2), we obtain the following series solution:

$$u(t)=1+t+\frac{t^2}{2!}+\frac{t^3}{3!}+\frac{t^4}{4!}+\cdots +\frac{t^k}{k!}+\cdots .$$

The closed form of the above series solution is $u(t)=e^t$, which is the exact solution of equation (5).

The same equation was solved by Evans and Raslan [29] using the Adomian decomposition method with complicated calculations of Adomian’s polynomials. Ghomanjani and Farahi [30] solved equation (5) using the Bezier control points method and obtained only approximation solution in the form

$$u(t)=1+0.822827885t+0.8954539433t^2.$$

Example 2 Consider the following delay differential equation of the third order:

$$u^{‴}(t)=-1+2u^2\left(\frac{t}{2}\right),u(0)=0,u^{\prime }(0)=1,u^{″}(0)=0.$$

(8)

Using the differential transformation method, the differential transform version of equation (8), we get

$$(k+3)(k+2)(k+1)U(k+3)=-\delta (k)+2\sum _{l=0}^k\frac{1}{2^l}U(l)\frac{1}{2^{k-l}}U(k-l)$$

(9)

and the differential transform version of the initial conditions $u(0)=0$, $u^{\prime }(0)=1$, $u^{″}(0)=0$ gives

$$U(0)=0,U(1)=1,U(2)=0.$$

From (9) we have

$$U(k+3)=\frac{1}{(k+3)(k+2)(k+1)}[-\delta (k)+2\sum _{l=0}^k\frac{1}{2^k}U(l)U(k-l)],k\ge 0.$$

(10)

Solving recurrence equations (10), we get

$$\begin{array}{c}U(3)=\frac{1}{6}[-1+2U{(0)}^2]=-\frac{1}{6}=\frac{1}{3!},\hfill \\ U(4)=\frac{1}{24}2[\frac{1}{2}U(0)U(1)+\frac{1}{2}U(1)U(0)]=0,\hfill \\ U(5)=\frac{1}{60}2[\frac{1}{4}U(0)U(2)+\frac{1}{4}{U}^2(1)+\frac{1}{4}U(0)U(2)]=\frac{1}{120}=\frac{1}{5!},\hfill \\ U(6)=\frac{1}{120}2[\frac{1}{8}U(0)U(3)+\frac{1}{8}U(1)U(2)+\frac{1}{8}U(2)U(1)+\frac{1}{8}U(3)U(0)]=0,\hfill \\ ⋮\hfill \end{array}$$

Thus

$$U(k)=\{\begin{array}{cc}0,\hfill & k=2n,\hfill \\ \frac{{(-1)}^n}{(2n+1)!},\hfill & k=2n+1,\hfill \end{array}$$

where $n\in \mathbb{N}\cup \{0\}$. From here and using the inverse transformation rule (2), we obtain series solution in the form

$$u(t)=\sum _{n=0}^{\mathrm{\infty }}\frac{{(-1)}^n}{(2n+1)!}{t}^n=sint,$$

which is the exact solution of equation (8). Evans and Raslan [29] solved equation (8) using the Adomian decomposition method and obtained a sequence of approximate solutions in the form of triple integrals with Adomian’s polynomials that required many symbolic calculations to obtain approximate solutions of (8). Saeed and Rahman [31] also solved equation (8) using the differential transformation method, but they transformed equation (8) into a system of three differential equations, which is a uselessly complicated approach to solving equation (8).

Example 3 Consider the following delay differential equation of the second order:

$$u^{″}(t)=u^{\prime }(t)+2u^2\left(\frac{t}{2}\right)-3u\left(\frac{t}{3}\right)u\left(\frac{t}{2}\right)-2t+2,u(0)=u^{\prime }(0)=0.$$

(11)

Applying the differential transformation method to equation (11), we get

$$\begin{array}{rcl}(k+2)(k+1)U(k+2)& =& (k+1)U(k+1)+2\sum _{l=0}^k\frac{1}{2^l}U(l)\frac{1}{2^{k-l}}U(k-l)\\ -3\sum _{l=0}^k\frac{1}{3^l}U(l)\frac{1}{2^{k-l}}U(k-l)-2\delta (k-1)+2\delta (k)\end{array}$$

(12)

and for initial conditions $u(0)=u^{\prime }(0)=0$, we have $U(0)=U(1)=0$. From (12), we obtain recurrence equations

$$\begin{array}{c}U(k+2)\hfill \\ =\frac{1}{k+2}U(k+1)+\frac{1}{(k+2)(k+1)}\hfill \\ \times [2\sum _{l=0}^k\frac{1}{2^k}U(l)U(k-l)-3\sum _{l=0}^k\frac{1}{3^l}\frac{1}{2^{k-l}}U(l)U(k-l)-2\delta (k-1)+2\delta (k)].\hfill \end{array}$$

(13)

Solving recurrence equations (13), we have

$$\begin{array}{l}U(2)=\frac{1}{2}U(1)+\frac{1}{2}[2U^2(0)-3U^2(0)+2]=1,\\ U(3)=\frac{1}{3}U(2)+\frac{1}{6}[2(\frac{1}{2}U(0)U(1)+\frac{1}{2}U(1)U(0))\\ \phantom{U(3)=}-3(\frac{1}{2}U(0)U(1)+\frac{1}{3}U(1)U(0))-2]=0,\\ U(4)=\frac{1}{4}U(3)+\frac{1}{12}[U(0)U(2)+\frac{1}{2}{U}^2(1)\\ \phantom{U(4)=}-3(\frac{1}{4}U(0)U(2)+\frac{1}{6}{U}^2(1)+\frac{1}{9}U(2)U(0))]=0,\\ ⋮\end{array}$$

Thus $U(k)=0$, $k\ge 3$. Using the inverse transformation rule (2), we obtain the exact solution $u(t)=t^2$.

Example 4 Consider the nonlinear pantograph-type integro-differential equation of the first order

$$u^{\prime }(t)+(\frac{1}{2}t-2)u(t)-2{\int }_0^t{u}^2\left(\frac{s}{2}\right)ds=1,$$

(14)

subject to the initial condition $u(0)=0$. Substituting $t=0$ in integro-differential equation (14), we get $u^{\prime }(0)=1$. Then the differential transformed version of equation (14) has the form

$$\begin{array}{c}(k+1)U(k+1)+\sum _{l=0}^k(\frac{1}{2}\delta (l-1)-2\delta (l))U(k-l)\hfill \\ -\frac{2}{k}\sum _{l=0}^{k-1}\frac{1}{2^{k-1}}U(l)U(k-l-1)=\delta (k).\hfill \end{array}$$

(15)

Solving recurrence equations (15), we get

$$\begin{array}{c}2U(2)-2U(1)+\frac{1}{2}U(0)-2U^2(0)=0\Rightarrow U(2)=1,\hfill \\ 3U(3)+[-2U(2)+\frac{1}{2}U(1)]-U(0)U(1)=0\Rightarrow U(3)=\frac{1}{2!},\hfill \\ 4U(4)+[-2U(3)+\frac{1}{2}U(2)]-\frac{1}{6}[2U(0)U(2)+U^2(1)]=0\Rightarrow U(4)=\frac{1}{6}=\frac{1}{3!},\hfill \\ 5U(5)+[-2U(4)+\frac{1}{2}U(3)]-\frac{1}{8}[U(0)U(3)+U(1)U(2)]=0\Rightarrow U(5)=\frac{1}{24}=\frac{1}{4!},\hfill \\ ⋮\hfill \end{array}$$

From here and using the inverse transformation rule (2), we obtain a series solution in the form

$$u(t)=t+t^2+\frac{1}{2!}{t}^3+\frac{1}{3!}{t}^4+\frac{1}{4!}{t}^5+\cdots +\frac{1}{k!}{t}^{k+1}+\cdots .$$

The closed form of the above series solution is $u(t)=t{e}^t$, which is the exact solution of equation (14).

Abazari and Abazari [32] solved equation (14) but as the pantograph differential equation of the second order without using an integral transformation formula.

Example 5 Consider the following nonhomogeneous first-order integro-differential equation with proportional delay:

$$u^{\prime }(t)-u\left(\frac{t}{2}\right)-\frac{1}{2}u\left(\frac{t}{2}\right){\int }_0^{\frac{t}{3}}u(s)u\left(\frac{s}{2}\right)ds=4-2t-\frac{8}{81}{t}^4,$$

(16)

subject to initial condition $u(0)=0$. Substituting $t=0$ in equation (16), we obtain the second condition $u^{\prime }(0)=4$. Now, applying the differential transformation method to equation (16), we get

$$\begin{array}{c}(k+1)U(k+1)-\frac{1}{2^k}U(k)-\frac{1}{2}\sum _{l=0}^{k-1}\sum _{s=0}^{k-l-1}\frac{1}{k-l}\frac{1}{3^{k-l}}\frac{1}{2^{k-s-1}}U(l)U(s)U(k-l-s-1)\hfill \\ =4\delta (k)-2\delta (k-1)-\frac{8}{81}{t}^4\hfill \end{array}$$

and for initial conditions $u(0)=0$, $u^{\prime }(0)=4$, we have $U(0)=0$, $U(1)=4$. Following the same procedure as in the above mentioned examples, we get

$$\begin{array}{c}2U(2)-\frac{1}{2}U(1)-\frac{1}{6}{U}^3(0)=-2\Rightarrow U(2)=0,\hfill \\ 3U(3)-\frac{1}{4}U(2)-\frac{1}{2}[\frac{1}{18}{U}^2(0)U(1)+\frac{1}{9}U(0)U(1)U(0)+\frac{1}{6}{U}^2(1)U(0)]=0\hfill \\ \Rightarrow U(3)=0,\hfill \\ ⋮\hfill \end{array}$$

Similarly, we obtain $U(k)=0$, $k\ge 2$. Using the inverse transformation rule (2), we get the exact solution $u(t)=4t$. A homogeneous form of equation (16) subject to initial conditions $u(0)=u^{\prime }(0)=1$ was solved by Abazari and Kilicman [27]. They obtained the closed form of a series solution in the form $u(t)=e^t$.

5 Conclusion

In the present paper, we have shown that the differential transformation method can be successfully used for solving nonlinear differential and integro-differential equations with proportional delays. New theorems are introduced with their proofs, and as application some examples are carried out. The main advantage of this method is that it can be applied directly to functional differential and integro-differential equations without requiring linearization, discretization or perturbation. Another important advantage is that this method is capable of greatly reducing the size of computational work and, moreover, the proposed method reduces the solution of a problem to the solution of a system of recurrence algebraic equations.