1 Introduction

The polytropic equations of state are appropriate in many situations in the context of General Relativity as well as in astrophysical problems. For example, it is well known that astrophysical objects as cores of stars, fully convective low-mass stars, white dwarfs, neutron stars and galactic halos can be modelled with matter which fullfills a polytropic equation of state [1,2,3,4,5,6,7,8,9,10,11]. In addition, polytropic equations of state have been considered in a cosmological context in order to model the matter content [12].

Recently, black hole (hereafter BH) solutions have been obtained considering polytropic equations of state [13]. In that work, the authors map the negative cosmological coupling with an effective pressure, demanding that it obeys a polytropic equation of state. After that, the matter content degrees of freedom are eliminated from the Einstein field equations and, finally, solutions matching polytropic thermodynamics with that of BHs are obtained.

The aforementioned solutions are obtained in the context of classical gravity. However, it is very well known that a more complete description quantum effects must be considered. As the full theory of quantum gravity is still lacking, a great variety of work has been devoted to getting some insight into the underlying physics (for an incomplete list, check [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32] and for a review see [33, 34]). Despite the fact that in that work the authors discuss different aspects of quantum gravity, most of them have the common feature that the resulting effective gravitational action acquires a scale-dependence. This behaviour is observed through the couplings of the effective action: they change from fixed values to scale-dependent quantities, i.e. \(\{G_0, \varLambda _0\} \mapsto \{G_k, \varLambda _k\}\), where \(G_0\) is Newton’s coupling and \(\varLambda _0\) is the cosmological coupling. Indeed, there is some evidence which supports that this scaling behaviour is consistent with Weinberg’s Asymptotic Safety program [35,36,37,38,39,40,41,42]. In addition, the effective action assuming running couplings has been studied in three-dimensional space-times in the context of BH physics in Refs. [43,44,45,46,47,48], in four dimensions [49] and in the cosmological context [50]. In the aforementioned work, the corresponding scale-dependent couplings take into account a quantum effect, namely, this approach admits corrections to both the classical BH backgrounds and the FLRW universe.

Then, inspired by this fact, the next step is to take advantage of the aforementioned approach to produce interesting BH solutions in new scenarios. The Van der Waals black hole [51] is a recent solution which, after identifying P with the cosmological constant \(\varLambda \), allow us to write down a BH equation of state \(P=P(V, T )\) and to compare it to the corresponding fluid equation of state [51]. We remark that this fact opened a window to investigate the analogy between BHs and certain fluids (for a recent review, see [52]).

In this work, inspired by this idea, we study how a polytropic BH in four-dimensional space-time obtained in Ref. [13] is generalized to the case of scale-dependent couplings, implemented and set at the level of an effective action.

The work is organized as follows: In Sect. 2 we introduce and summarize the polytropic BH solution, whereas Sect. 3 is devoted to a brief introduction of the scale-dependent gravitational setting, which is employed in Sect. 4 to obtain the scale-dependent BH solution. Along this section, the new solution is carefully studied with emphasys on horizons, asymptotics, singularities, thermodynamics and their comparison with the previously studied classical polytropic solution. Finally, some concluding remarks are given in Sect. 5.

2 Polytropic black hole solution

In this section we summarize the main results obtained in Ref. [13]. The line element is parametrized as

$$\begin{aligned}&\mathrm {d} s^{2}=-f_{0}(r) \mathrm {d} t^{2}+f_{0}(r)^{-1} \mathrm {d}r^{2}+r^{2}\mathrm {d}\varOmega ^{2}, \end{aligned}$$
(1)

where the lapse function is computed to be

$$\begin{aligned}&f_{0}(r,P_{0})=\frac{r^{2}}{L^{2}}-\frac{2G_{0}M_{0}}{r}+h(r,P_{0}). \end{aligned}$$
(2)

On the one hand, the parameter \(P_0\) is associated with a negative cosmological constant, \(\varLambda _0\), and with the parameter \(L^{2}\) by

$$\begin{aligned} P_{0}:=-\frac{\varLambda _{0}}{8\pi G_{0}}=\frac{3}{8\pi G_{0} L^{2}} =\frac{3}{\kappa _0 L^2}. \end{aligned}$$
(3)

In addition, note that \(\kappa _0\) is the so-called Einstein constant, which is defined in terms of the Newton coupling, \(\kappa _0 \equiv 8\pi G_0\). On the other hand, \(P_{0}\) is taken as the pressure of a polytropic gas with equation of state

$$\begin{aligned} P_{0}=K\varrho ^{1+\frac{1}{n}}, \end{aligned}$$
(4)

where \(\varrho \) is the polytropic gas density, K is a positive constant and n is the polytropic index, which takes values \(0\le n<\infty \) [53].

In order to obtain the unknown function \(h(r,P_{0})\), the authors of Ref. [13] assume that

  • The metric (1) is a solution of the Einstein field equations \(G_{\mu \nu }+g_{\mu \nu }\varLambda _{0} = \kappa _0 T_{\mu \nu }\) with \(\varLambda _0<0\) and \(T^{\mu }_{\nu }=\text {diag}(-\varrho ,p_{1},p_{2},p_{3})\).

  • The thermodynamics of the BH solution is matched with that of a polytropic gas after eliminating the matter degrees of freedom from the Einstein field equations.

With these assumptions, \(h(r,P_{0})\) reads

$$\begin{aligned}&h = C_1 r^{\frac{1-n}{1+n}} \left( K^{-\frac{n}{n+1}}+P_{0}^{\frac{1}{n+1}}\right) +\frac{C_2}{r}+\frac{1}{3} \kappa _0 P_{0} r^2. \end{aligned}$$
(5)

In particular, for \(n=-\frac{1}{3}\), \(C_{2}=0\) and

$$\begin{aligned} C_{1}=-\frac{1}{3} \kappa _0 P_{0}\left( K^{-\frac{n}{1+n}}+P_{0}^{\frac{1}{1+n}}\right) ^{-1}. \end{aligned}$$
(6)

Therefore, one obtains

$$\begin{aligned}&f_{0}=\frac{r^{2}}{L^{2}}-\frac{2G_{0}M_{0}}{r}, \end{aligned}$$
(7)
$$\begin{aligned}&\rho _{0}=-p_{1}=\frac{1}{\kappa _0 r^{2}}, \end{aligned}$$
(8)
$$\begin{aligned}&p_{2}=p_{3}=0. \end{aligned}$$
(9)

Note that, for this choice of the integration constants, the parameters \(\rho _{0}\) and \(p_{i}\) (\(i=1,2,3\)) describe a perfect fluidFootnote 1 as a matter–source of the Einstein field equations and the space-time results asymptotically anti-de Sitter.

It is worth mentioning that, in this case, the matter content does not depend on the constant K appearing in the polytropic equation of state for the dark energy content. However, this is not true in general because the result could be affected by the particular choice of the polytropic index n.

It is remarkable that \(T_{\mu \nu }\) fullfils all the energy conditions

$$\begin{aligned}&\rho _{0}\ge 0,\quad \rho _{0}+p_{i}\ge 0, \end{aligned}$$
(10)
$$\begin{aligned}&\rho _{0}+\sum \limits _{i}p_{i}\ge 0,\quad \rho _{0}+p_{i}\ge 0, \end{aligned}$$
(11)
$$\begin{aligned}&\rho _{0}\ge |p_{i}|, \end{aligned}$$
(12)

which are referred as the weak, strong and dominant energy conditions, respectively.

Besides, the knowledge of the invariants (scalars) allows one to check if the theory presents some singularity. Thus, the corresponding scalars are computed below:

$$\begin{aligned}&R_{0}=2 \left( \frac{1}{r^2}-\frac{6}{L^2}\right) , \end{aligned}$$
(13)
$$\begin{aligned}&\text {Ricc}_{0}= 2 \left( \frac{18}{L^4}-\frac{6}{L^2 r^2}+\frac{1}{r^4}\right) , \end{aligned}$$
(14)
$$\begin{aligned}&{\mathcal {K}}_{0}=\frac{4 \left( L^4 \left( 12 M_{0}^2+4 M_{0} r+r^2\right) -2 L^2 r^4+6 r^6\right) }{L^4 r^6}, \end{aligned}$$
(15)

where \(R_0\), \(\text {Ricc}_{0}\) and \({\mathcal {K}}_{0}\) are the classical Ricci, Ricci squared and Kretschmann scalars, respectively. One observes that they have a divergence at \(r=0\). In this sense, the BH solution is singular. In order to get insight into the thermodynamics properties of this BH, we obtain the event horizon which is located at

$$\begin{aligned}&r_{0}= \left( 2G_{0}M_{0} L^2 \right) ^{1/3}. \end{aligned}$$
(16)

Rewriting the lapse function in terms of the event horizon we have

$$\begin{aligned} f_{0}(r)=\frac{1}{L^2 r}\left( r^3 - r_{0}^3\right) . \end{aligned}$$
(17)

The thermodynamic behaviour of the BH can be characterized by the corresponding Hawking temperature, \(T_{0}\), and the Bekenstein–Hawking entropy, \(S_{0}\), which are given by

$$\begin{aligned}&T_{0} = \frac{1}{4\pi }\left| \lim _{r \rightarrow r_0}\frac{\partial _r g_{tt}}{\sqrt{-g_{tt} g_{rr}}}\right| = \frac{3}{4\pi }\left| \frac{r_{0} }{L^{2}}\right| , \end{aligned}$$
(18)
$$\begin{aligned}&S_{0} = \frac{{\mathcal {A}}_H(r_0)}{4 G_0}. \end{aligned}$$
(19)

Note that \({\mathcal {A}}_H\) is the horizon area which is given by

$$\begin{aligned}&{\mathcal {A}}_H(r_0) \equiv \oint \mathrm {d}x^{2} \sqrt{h} =4 \pi r_0^2, \end{aligned}$$
(20)

where \(h_{ij}\) is the induced metric at the event horizon \(r_0\). After this brief summary of the polytropic BH, in the next section we will study the scale-dependent setting.

3 Scale-dependent coupling and scale setting

The scale-setting procedure presented in the first part of this section follows closely the spirit and concept of Ref. [43]. The scale-dependent effective action in the Einstein–Hilbert truncation reads

$$\begin{aligned} \varGamma [g_{\mu \nu },k]=\int \mathrm {d}^{4}x\sqrt{-g}\bigg [\frac{1}{2 \kappa _k} (R-2\varLambda _{k}) +{\mathcal {L}}^{\text {M}}_k\bigg ], \end{aligned}$$
(21)

where \(G_{k}\) and \(\varLambda _{k}\) stand for the scale-dependent gravitational and cosmological coupling, respectively, whereas \(\kappa _k \equiv 8 \pi G_k\) is the scale-dependent Einstein coupling and \({\mathcal {L}}_{k}^{\text {M}}\) is the Lagrangian density for the matter content.

Variations with respect to the metric field \(g_{\mu \nu }\), give the modified Einstein field equations

$$\begin{aligned} G_{\mu \nu }+g_{\mu \nu }\varLambda _{k}=8\pi G_{k}T^{\text {eff}}_{\mu \nu }, \end{aligned}$$
(22)

where \(T^{\text {eff}}_{\mu \nu }\) is the effective energy-momentum tensor defined as

$$\begin{aligned} T^{\text {eff}}_{\mu \nu }:=(T^{\text {M}}_{k})_{\mu \nu } - \frac{1}{8\pi G_{k}}\varDelta t_{\mu \nu }. \end{aligned}$$
(23)

In Eq. (23), \((T^{\text {M}}_{k})_{\mu \nu }\) is the matter energy-momentum tensor and \(\varDelta t_{\mu \nu }\) is given by

$$\begin{aligned} \varDelta t_{\mu \nu }=G_{k}\left( g_{\mu \nu }\square -\nabla _{\mu }\nabla _{\nu }\right) G_{k}^{-1}. \end{aligned}$$
(24)

Please note that the renormalization scale k is, indeed, not constant anymore, which means that the stress energy tensor is likely not conserved, as was discussed previously in Ref. [46]. This kind of problem has been considered in the context of renormalization group improvement of BHs in asymptotic safety scenarios (see, for instance [54,55,56,57] and the references therein).

This inconsistency with very fundamental conservation laws can be avoided by applying the variational scale-setting procedure described in Ref. [43], where the metric equations of motion (22) are complemented by an equation obtained from variations with respect to the scale-field k(x)

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d} k} \varGamma [g_{\mu \nu }, k] =0. \end{aligned}$$
(25)

It is worth mentioning that, if the precise beta functions of the problem are not known, Eqs. (21) and (25) do not have enough information in order to solve for the two independent fields, \(g_{\mu \nu }(x)\) and k(x). In order to solve this problem, we take into account the so-called null energy condition and assume that the couplings \(\{G_k\), \(\varLambda _k\}\) depend explicitly on space-time coordinates, a dependence which is inherited from the space-time dependence of k(x). Thus, as reported in Refs. [43,44,45,46, 49, 50], we can encode the ignorance on the scale-dependence of the coupling parameters by promoting \(G_{k}\) and \(\varLambda _{k}\) to independent fields, G(x) and \(\varLambda (x)\), and considering Eq. (22) with some extra assumption in order to solve for the unknown functions.

In this work we follow the approach presented in Refs. [43,44,45,46, 49, 50]. Moreover, we assume a static and spherically symmetric space-time and a line element parametrized as

$$\begin{aligned} \text {d}s^2=-f(r)\text {d}t^2 + f(r)^{-1} \text {d}r^2+r^2 \text {d}\varOmega ^2. \end{aligned}$$
(26)

Note that replacing Eq. (26) in Eq. (22) we shall obtain two independent differential equations for the three independent fields f(r), G(r) and \(\varLambda (r)\). An alternative way to decrease the number of degrees of freedom consists in demanding some energy condition on \(T^{\text {eff}}_{\mu \nu }\) [58]. It is well known that the null energy condition is the least restrictive of the usual energy conditions and that it can help to obtain suitable solutions of the Einstein field equations [44]. For \(T^{\text {eff}}_{\mu \nu }\), the null energy condition is

$$\begin{aligned} T^{\text {eff}}_{\mu \nu }\ell ^{\mu }\ell ^{\nu } \ge 0, \end{aligned}$$
(27)

which reads

$$\begin{aligned} \left[ (T^{\mathrm {M}})_{\mu \nu } - \frac{1}{8\pi G(r)}\varDelta t_{\mu \nu }\right] \ell ^{\mu }\ell ^{\nu } \ge 0, \end{aligned}$$
(28)

where \(\ell ^{\mu }\) is a null vector. Note that \((T^{\text {M}})_{\mu \nu }\) corresponds to the matter stress–energy tensor after replacing \(G_{0}\rightarrow G(r)\). Considering the special case \(\ell ^{\mu }=\{f^{-1/2},f^{1/2},0,0 \}\) we obtain \((T^{\mathrm {M}})_{\mu \nu }\ell ^{\mu }\ell ^{\nu }=0\), which implies that \(\varDelta t_{\mu \nu }\ell ^{\mu }\ell ^{\nu }\ge 0\). However, it can be shown that \(G_{\mu \nu }\ell ^{\mu }\ell ^{\nu }=0\) and, thus by virtue of (22), one finds

$$\begin{aligned} \varDelta t_{\mu \nu }\ell ^{\mu }\ell ^{\nu }=0. \end{aligned}$$
(29)

This equation encodes the radial dependence of Newton’s coupling G(r) [47]. In particular, the corresponding differential equation is

$$\begin{aligned} 2\left[ \frac{\mathrm {d} G(r)}{\mathrm {d} r}\right] ^2 = G(r)\frac{\mathrm {d}^2 G(r) }{\mathrm {d} r^2 }. \end{aligned}$$
(30)

Therefore, solving Eq. (30) we obtain

$$\begin{aligned} G(r)=\frac{G_{0}}{1+\epsilon r}, \end{aligned}$$
(31)

where \(\epsilon \ge 0\) is an integration constant with dimensions of inverse of length. Note that in the limit \(\epsilon \rightarrow 0\), \(G(r)=G_{0}\), which implies that \(\varDelta t_{\mu \nu }=0\) and thus, the classical Einstein field equations are recovered. Therefore, the strength of scale-dependence is controlled by the so-called running parameter \(\epsilon \).

4 Scale-dependent polytropic black hole

In this section we obtain solutions for the modified Einstein field equations

$$\begin{aligned} G_{\mu \nu }-8\pi G(r)P(r)g_{\mu \nu } = 8\pi G(r)(T^{\text {M}})_{\mu \nu } -\varDelta t_{\mu \nu }. \end{aligned}$$
(32)

In the above expression, G(r) is given by Eq. (31), \(P(r)=-\varLambda (r)/8\pi G(r)\) stands for the scale-dependent polytropic pressure and

$$\begin{aligned} (T^{\text {M}})^{\mu }_{\nu } = \text {diag}(-{\tilde{\rho }},{\tilde{p}},0,0) , \end{aligned}$$
(33)

with \({\tilde{\rho }}=-{\tilde{p}}=1/(8\pi G(r)r^2)\). Besides, it should be noted that the scale-dependent pressure is linked with the energy density through a fixed number and not by some scale-dependent coupling. This is because we encode the scale-dependence into the pressure and the energy density, assumption which is always possible. More precisely, the parametrization of \({\tilde{\rho }}\) and \({\tilde{p}}\) can be thought of as a generalization of the classical results in Eq. (8) after the incorporation of the scale-dependent coupling G(r).

4.1 Solutions

The solution for the scale-dependent polytropic BH is given by

$$\begin{aligned} f(r)&= f_{0}(r)+6 G_{0} M_{0} r^2 \epsilon ^3 \ln \left[ 2 G_{0} M_{0} \frac{r \epsilon +1}{r}\right] \nonumber \\&\quad +3G_{0}M_{0}\epsilon (1-2 r \epsilon ), \end{aligned}$$
(34)
$$\begin{aligned} P(r)&=(2 r \epsilon +1)P_{0} -\frac{3 M_{0}}{8 \pi }\frac{ (12 r \epsilon (r \epsilon +1)+1)\epsilon ^2}{ r (r \epsilon +1) } \nonumber \\&\quad +\frac{18 G_{0} M_{0} \epsilon ^3 (2 r \epsilon +1)}{8 \pi G_{0} } \ln \left[ 2 G_{0} M_{0}\frac{ r \epsilon +1}{r}\right] , \end{aligned}$$
(35)
$$\begin{aligned} {\tilde{\rho }}(r)&=-{\tilde{p}}=(1+\epsilon r)\rho _{0} =\frac{1+ \epsilon r}{8\pi G_{0} r^2}, \end{aligned}$$
(36)
$$\begin{aligned} G(r)&= \frac{G_{0}}{1+\epsilon r}, \end{aligned}$$
(37)

Note that our solution reproduces the classical results given by Eqs. (7), (8) and (3) in the limit \(\epsilon \rightarrow 0\). In fact,

$$\begin{aligned}&\lim \limits _{\epsilon \rightarrow 0}f(r) = \frac{r^{2}}{L^{2}}-\frac{2G_{0}M_{0}}{r}, \end{aligned}$$
(38)
$$\begin{aligned}&\lim \limits _{\epsilon \rightarrow 0}{\tilde{\rho }}(r) = \frac{1}{8\pi G_{0}r^2}, \end{aligned}$$
(39)
$$\begin{aligned}&\lim \limits _{\epsilon \rightarrow 0}{\tilde{p}}(r) = -\frac{1}{8\pi G_{0}r^2}, \end{aligned}$$
(40)
$$\begin{aligned}&\lim \limits _{\epsilon \rightarrow 0}P(r) = -\frac{\varLambda _0}{8\pi G_{0}}=\frac{3}{8\pi G_{0} L^{2}}, \end{aligned}$$
(41)

as expected.

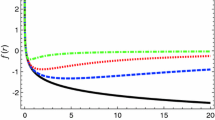
In Fig. 1 the lapse function is shown for different values of \(\epsilon \) compared to the classical BH solution,

Fig. 1
figure 1

Lapse function for \(\epsilon =0.00\) (black solid line), \(\epsilon =0.75\) (dashed blue line), \(\epsilon =1.50\) (short dashed red line) and \(\epsilon =2.00\) (dotted green line). The other values have been taken as unity. See text for details

Full size image

showing that, for small \(\epsilon \) values, the scale-dependent lapse function coincides with the classical one. However, when \(\epsilon \) increases, a deviation from the classical solution appears. In particular, when \(r\rightarrow \infty \),

$$\begin{aligned}&f(r) \approx \frac{r^2}{L^2} + 6 G_{0} M_{0} r^2 \epsilon ^3 \ln (2 G_{0} M_{0} \epsilon ). \end{aligned}$$
(42)

We note that, asymptotically, the scale-dependent effect only dominates when high values of the running parameter \(\epsilon \) are considered. In addition, as Eq. (42) shows, the scale-dependent lapse function behaves asymptotically as anti-de Sitter as in the classical case but with an effective cosmological constant given by

$$\begin{aligned} \varLambda _{eff}=-\left[ \frac{1}{L^2}+6 G_{0} M_{0} \epsilon ^3 \ln (2 G_{0} M_{0} \epsilon )\right] , \end{aligned}$$
(43)

provided

$$\begin{aligned} \epsilon > (2G_{0} M_{0})^{-1}, \end{aligned}$$
(44)

or

$$\begin{aligned}&\epsilon < (2G_{0} M_{0})^{-1}, \end{aligned}$$
(45)
$$\begin{aligned}&\frac{1}{L^{2}} > -6 G_{0} M_{0} \epsilon ^3 \ln (2 G_{0} M_{0} \epsilon ). \end{aligned}$$
(46)

We note that in the case

$$\begin{aligned} \begin{aligned}&\epsilon< (2G_{0} M_{0})^{-1},\\&\frac{1}{L^2} < -6 G_{0} M_{0} \epsilon ^3 \ln (2 G_{0} M_{0} \epsilon ), \end{aligned} \end{aligned}$$
(47)

this effective cosmological constant becomes a negative quantity and the solution asymptotically turns into de Sitter space. Even more, in the case

$$\begin{aligned} \begin{aligned}&\epsilon < (2G_{0} M_{0})^{-1},\\&\frac{1}{L^2} = -6 G_{0} M_{0} \epsilon ^3 \ln (2 G_{0} M_{0} \epsilon ), \end{aligned} \end{aligned}$$
(48)

the effective cosmological constant vanishes and the asymptotic (anti-) de Sitter behaviour disappears. In other words, the running parameter could be the responsible of certain topology change in the solution. A similar result can be found in Ref. [49], where an effective cosmological constant appears when the asymptotic behaviour of a certain scale-dependent spherically symmetric space-time with cosmological coupling is considered.

The behaviour of the scale-dependent polytropic pressure is shown in Fig. 2.

Fig. 2
figure 2

Polytropic pressure function for \(\epsilon =0.00\) (black solid line), \(\epsilon =0.05\) (dashed blue line), \(\epsilon =0.10\) (short dashed red line), \(\epsilon =0.25\) (dotted green line). The other values have been taken as unity

Full size image

It can be seen that, depending on \(\epsilon \), P(r) diverges at \(r\rightarrow 0\) to \(-\infty \) and behaves as

$$\begin{aligned} P(r)\approx \frac{3 (2 r \epsilon +1) }{8 \pi G_{0}}\left[ \frac{1}{L^2}+6 G_{0} M_{0} \epsilon ^3 \ln (2 G_{0} M_{0} \epsilon )\right] , \end{aligned}$$
(49)

in the limit \(r\rightarrow \infty \). Even more, the asymptotic value of P(r) in Eq. (49) can be a negative value whenever

$$\begin{aligned} \begin{aligned}&\epsilon< (2G_{0} M_{0})^{-1},\\&\frac{1}{L^2} < -6 G_{0} M_{0} \epsilon ^3 \ln (2 G_{0} M_{0} \epsilon ), \end{aligned} \end{aligned}$$
(50)

which coincides with the condition demanded for a de Sitter asymptotic behaviour of f(r) in Eq. (47).

Figure 3 shows the scale-dependent density profile \({\tilde{\rho }}\) for different values of \(\epsilon \). It can be seen that \({\tilde{\rho }}\) increases with the running parameter \(\epsilon \). More precisely, \({\tilde{\rho }}\) decreases slowly compared with the classical density. In fact, when \(r\rightarrow \infty \), \({\tilde{\rho }}\sim r^{-1}\). Regarding the matter content, we remark that \((T^{\text {M}})_{\mu \nu }\) fulfills all the energy conditions as in the classical case.

Fig. 3
figure 3

Scale-dependent density for \(\epsilon =0.00\) (black solid line), \(\epsilon =1.00\) (dashed blue line), \(\epsilon =2.00\) (short dashed red line), \(\epsilon =3.00\) (dotted green line). The other values have been taken as unity. See text for details

Full size image

We end this section noticing that the singularity at \(r=0\) cannot be removed in the scale-dependent context. In fact, for small \(\epsilon \), the curvature scalars are given by

$$\begin{aligned}&R \approx R_{0}-\frac{6 G_{0} M_{0}}{r^2}\epsilon , \end{aligned}$$
(51)
$$\begin{aligned}&\text {Ricc} \approx \text {Ricc}_{0}+\frac{12 G_{0} M_{0}}{r^4} \left( \frac{3 r^2}{L^2}-1\right) \epsilon , \end{aligned}$$
(52)
$$\begin{aligned}&{\mathcal {K}} \approx {\mathcal {K}}_{0}-\frac{48 G_{0}^{2} M_{0}^{2}}{ r^5}\epsilon \ -\frac{24 G_{0} M_{0}}{ r^4}\left( 1-\frac{r^2}{L^2}\right) \epsilon , \end{aligned}$$
(53)

showing that the classical results are recovered in the limit \(\epsilon \rightarrow 0\) and that the singularity persists at \(r=0\). Furthermore, \(R\sim r^{-2}\), \(\text {Ricc}\sim r^{-4}\) and \({\mathcal {K}}\sim r^{-6}\) for \(r\rightarrow 0\), in agreement with the classical case.

4.2 Horizons and black hole thermodynamics

In order to study the thermodynamics of the scale-dependent polytropic BH, the horizon radius, \(r_{H}\), must be computed. As it is well known, \(r_{H}\) can be obtained as one of the real positive roots of the lapse function, f(r). However, demanding \(f(r_H)=0\) in our solution, leads to a transcendental equation for r which must be solved numerically. Besides, we can solve for \(\epsilon \ll 1\) to obtain

$$\begin{aligned} r_{H} \approx \left[ \frac{\left( \sqrt{2 r_{0}^3 \epsilon ^3+4}+2\right) ^{2/3}-2^{1/3} r_{0} \epsilon }{\left( 4\left( \sqrt{2 r_{0}^3 \epsilon ^3+4}+2 \right) \right) ^{1/3}} \right] r_0 , \end{aligned}$$
(54)

where \(r_{0}=\root 3 \of {2L^{2}G_{0}M_{0}}\) is the classical horizon defined in Sect. 4. In particular, if we take the limit of Eq. (54) when \(\epsilon \rightarrow 0\) one obtains that \(r_H = r_0\), as one should. It can be seen that, for small \(M_{0}\), the horizon radius obtained by both methods coincides with the classical one (see Fig. 4).

Fig. 4
figure 4

Horizon radius as a function of \(M_{0}\) for \(\epsilon =0.05\), \(L=2\) and \(G_{0}=0.8\). The plots for the numerical solution, the expansion for \(\epsilon \ll 1\) and the classical case correspond to the black solid line, dashed blue line and short dashed red line, respectively

Full size image

Moreover, the scale-dependent \(r_{H}\) deviates from the classical horizon as \(M_{0}\) increases. In order to get more insight into the thermodynamics of the scale-dependent polytropic BH we shall calculate the Hawking temperature, \(T_{H}\), and the Bekenstein–Hawking entropy, \(S_{\text {BH}}\). It is remarkable that, although \(r_{H}\) cannot be obtained analytically, we can obtain \(T_{H}\) and \(S_{\text {BH}}\) as implicit functions of the horizon radius. In fact,

$$\begin{aligned}&T_{H} = \frac{3 G_{0} M_{0}}{2\pi r_{H}^2 (\epsilon r_{H} +1 )}, \end{aligned}$$
(55)
$$\begin{aligned}&S_{\text {BH}} = \frac{{\mathcal {A}}_{H}}{4G(r_H)} = S_0 \cdot (1 + \epsilon r_H ), \end{aligned}$$
(56)

as can be checked by the reader. However, the behaviour of these thermodynamics quantities as a function of the classical BH mass \(M_{0}\), must be obtained after a numerical analysis is performed.

In Fig. 5 we compare the behaviour of \(T_{H}\) obtained numerically as a function of \(M_{0}\) with the classical result and the one obtained for \(\epsilon \ll 1\) which reads

$$\begin{aligned} T_{H}\approx & {} T_0 + \frac{15 r_{0}^3 \epsilon ^2}{16 \pi L^2}. \end{aligned}$$
(57)
Fig. 5
figure 5

Hawking temperature as a function of \(M_{0}\) for \(\epsilon =0.05\), \(L=2\) and \(G_{0}=0.8\). The plots for the numerical solution, the expansion for \(\epsilon \ll 1\) and the classical case correspond to the black solid line, dashed blue line and short dashed red line, respectively

Full size image

As in the previous case, the temperatures coincide for small classical BH mass and a deviation is observed as \(M_{0}\) increases.

A similar analysis is shown in Fig. 6 for the entropy. In this case, the behaviour of \(S_{\text {BH}}\) obtained numerically as a function of \(M_{0}\) is compared with the classical result and the obtained for \(\epsilon \ll 1\) which reads

$$\begin{aligned} S_{\text {BH}}\approx & {} S_{0}-\frac{5}{2} \pi L^{2} M_{0}^{3} r_{0}^3\epsilon ^2, \end{aligned}$$
(58)

as Fig. 6 shows.

Fig. 6
figure 6

Bekenstein–Hawking entropy as a function of \(M_{0}\) for \(\epsilon =0.07\), \(L=2\) and \(G_{0}=0.8\). The plots for the numerical solution, the expansion for \(\epsilon \ll 1\) and the classical case correspond to the black solid line, dashed blue line and short dashed red line, respectively

Full size image

As a final comment, we note that the classical behaviour of both the temperature and the entropy is not considerably affected by the runnig. In this sense, in spite the metric changes with small values of the runnig (including topology changes), the thermodynamics remains robust because the horizon remains close to the classical one.

5 Concluding remarks

In this article, we have studied for the first time the scale-dependence of a polytropic black hole in a spherically symmetric four-dimensional space-time assuming a non-null cosmological coupling. After presenting the model and the classical black hole solutions, we have allowed for a scale-dependence of the gravitational as well as the cosmological coupling, and we have solved the corresponding generalized field equations by imposing the null energy condition. Besides, we have studied in detail the horizon structure, asymptotics and some thermodynamic properties.

As a mandatory remark, one should note that the scale-dependent approach introduces an effective contribution to the energy momentum tensor thought \(\varDelta t_{\mu \nu }\). Moreover, in agreement with the classical solution, the Schwarzschild ansatz is preserved. Regarding the event horizon, it is important to mention that it is not analytical and therefore it is not possible to get an explicit expression for it. However, we are able to obtain a closed formula for the temperature and the entropy, writing those quantities in terms of the horizon radius. Note that, for small values of \(\epsilon \), the scale-dependent solutions are in agreement with the classical black hole, but when \(\epsilon \) take large values, a strong deviation appears.

In addition, and following the philosophy of the scale-dependent scenario, this novel solution (including the thermodynamic properties) should be quite similar to the classical counterpart. This is because we expect that the incorporation of quantum corrections slightly modifies the usual behavior, which is in agreement with Eqs. (54), (57) and (58).

As this is a general feature of several scale-dependent black hole solutions studied in the past [44, 46, 49], we conclude that black hole thermodynamics is robust against this kind of deformations of the gravitational theory.

To conclude, some final comments are in order. First, we would like to point out that all of the results obtained here are independent of the proportionality constant K appearing in the polytropic equation of state. Even more, the choice \(n=-1/3\) for the polytropic index and the particular fitting for the integration constants \(C_{1}\) and \(C_{2}\) in Sect. 2 lead to solutions which are unaffected by whether K depends on a certain scale or not. It can be shown that, for a different choice of the polytropic index and integration constants the matter sector must be modified incorporating the scale-dependence on K. Second, we note that, although we have extended the polytropic solution given in [13], the same technique could be applied to different exact polytrope solutions with cosmological constant reported in the past (see, for example [59, 60]). Third, from the point of view of a possible astrophysical test of the solution here presented, an important feature to be studied is the so-called static radius (frequently known as the turnaround radius) [61, 62], which defines the equilibrium region between gravitational attraction and dark energy repulsion. Interestingly, this radius, computed for several polytropic solutions, can be related to the maximum allowable size of a spherical cosmic structure as a function of its mass [10, 62,63,64]. In this sense, astrophysical observations of large-scale structures could indirectly shed light on possible bounds on the running parameter (which would enter as a new ingredient of the static radius), which would indicate deviations from general relativity.

These and other aspects, which are beyond the scope of the present work, are left for a future publication.