1 Introduction

During the last decades, the standard cosmological model, i.e., the cold dark matter with a cosmological constant (\(\varLambda \)CDM) model [1, 2] has been well established. It is consistent with several precise astronomical observations that involve the Wilkinson Microwave Anisotropy Probe (WMAP) [3], the Planck satellite [4], the Supernovae Cosmology Project [5], and so on. One of the most important and basic assumptions of the \(\varLambda \)CDM model is the cosmological principle, which states that the universe is homogeneous and isotropic on large scales. However, such a principle faces several challenges [6]. The Union2 SnIa data hint that the universe has a preferred direction pointing to \((l,b)=(309^\circ ,18^\circ )\) in the galactic coordinate system [7]. Toward this direction, the universe has the maximum acceleration of expansion. Astronomical observations [8] found that the dipole moment of the peculiar velocity field in the direction \((l,b)=(287^\circ \pm 9^\circ ,8^\circ \pm 6^\circ )\) in the scale of \(50~\mathrm{h}^{-1}~\mathrm{Mpc}\) has a magnitude \(407\pm 81~\mathrm{km}~\mathrm{s}^{-1}\). This peculiar velocity is much larger than the value \(110~\mathrm{km}~\mathrm{s}^{-1}\) constrained by WMAP5 [9]. The recently released data of the Planck Collaboration show deviations from isotropy with a level of significance (\({\sim }3\sigma \)) [10]. The Planck Collaboration confirms an asymmetry of the power spectra between two preferred opposite hemispheres. These facts hint that the universe may have certain preferred directions.

Both the \(\varLambda \)CDM model and the standard model of particle physics require no variation of fundamental physical constants in principle, such as the electromagnetic fine-structure constant \(\alpha _e=e^2/\hbar c\). Recently, the observations on quasar absorption spectra show that the fine-structure constant varies at cosmological scale [11, 12]. Furthermore, in high redshift region (\(z>1.6\)), they have shown that the variation of \(\alpha _e\) is well represented by an angular dipole model pointing in the direction \((l,b)=(330^\circ ,-15^\circ )\) with level of significance (\({\sim }4.2\sigma \)). Mariano and Perivolaropoulos [13] have shown that the dipole of \(\alpha _e\) is anomalously aligned with corresponding dark energy dipole obtained through the Union2 sample. One possible reason of the variation of \(\alpha _e\) is the variation of the speed of light, which means that Lorentz symmetry is violated on a cosmological scale. The fact that the universe may have a preferred direction also means that the isotropic symmetry of cosmology is violated. Also, the dipole direction of the fine-structure constant is aligned with the cosmological preferred direction. Such facts hint that the two astronomical observations, the cosmological preferred direction and the variation of \(\alpha _e\), may correspond to the same physical mechanism.

Finsler geometry is a possible candidate for investigating both the cosmological preferred direction and the dipole structure of the fine-structure constant. Finsler geometry [14] is a new geometry which involves Riemann geometry as its special case. Chern pointed out that Finsler geometry is just Riemann geometry without quadratic restriction, in his Notices of AMS. The symmetry of spacetime is described by the isometric group. The generators of isometric group are directly connected with the Killing vectors. It is well known that the isometric group is a Lie group in a Riemannian manifold. This fact also holds in a Finslerian manifold [15]. Generally, Finsler spacetime admits less Killing vectors than Riemann spacetime does [16]. The causal structure of Finsler spacetime is determined by the vanishing of the Finslerian length [17]. The speed of light is modified. It has been shown that the translation symmetry is preserved in flat Finsler spacetime [16]. Thus, the energy and momentum are well defined in Finsler spacetime.

The property of Lorentz symmetry breaking in flat Finsler spacetime makes Finsler geometry a possible mechanism of Lorentz violation [18, 19]. Historically, Bogoslovsky [20–24] first suggested a Finslerian metric, i.e., \(\mathrm{d}s=(\eta _{\mu \nu }\mathrm{d}x^\mu \mathrm{d}x^\nu )^{(1-b)/2}(n_\rho \mathrm{d}x^\rho )^b\), to investigate Lorentz violation. Here, \(\eta _{\mu \nu }\) is Minkowski metric and \(n_\rho \) is a constant null vector. Such a metric involves a Lorentz symmetry violation without violation of the relativistic symmetry [25, 26]. The relativistic symmetry is realized by means of the 3-parameter group of generalized Lorentz boosts. Later on the results obtained in Bogoslovsky’s work were mostly reproduced by Gibbons et al. [27], with the help of the techniques of continuous deformations of the Lie algebras and nonlinear realizations. Gibbons et al. have pointed out that the Bogoslovsky spacetime corresponds to General Very Special Relativity, which generalizes Glashow’s very special relativity [28–30]. In the same work [27] the 8-parametric isometry group [20, 31] of the Bogoslovsky spacetime was called \(\mathrm{DISIM}_b(2)\). Although the group \(\mathrm{DISIM}_b(2)\) is an 8-dimensional subgroup of the 11-dimensional Weyl group, pure dilations are not elements of \(\mathrm{DISIM}_b(2)\). The gravitational field equation in Finsler spacetime has been studied extensively [32–41]. Models [42–47] based on a Finsler spacetime have been developed to study the cosmological preferred directions.

We suggested that the vacuum field equation in Finsler spacetime is equivalent to the vanishing of the Ricci scalar [48]. The vanishing of the Ricci scalar implies that the geodesic rays are parallel to each other. The geometric invariant of Ricci scalar implies that the vacuum field equation is insensitive to the connection, which is an essential physical requirement. The Schwarzschild metric can be deduced from a solution of our field equation if the spacetime preserves spherical symmetry. Supposing spacetime to preserve the symmetry of the “Finslerian sphere”, we found a non-Riemannian exact solution of the Finslerian vacuum field equation [49]. In this paper, following a similar approach to our previous work [49], we present a modified Friedmann–Robertson–Walker (FRW) metric in Finsler spacetime, and then we use it to study the cosmological preferred direction and the dipole structure of the fine-structure constant.

The rest of the paper is arranged as follows. In Sect. 2, we briefly introduce the anisotropic universe in Finsler geometry. It can be seen easily that the speed of light in vacuum (so the fine-structure constant) is direction-dependent. In Sect. 3, we derive the gravitational field equation in a Finslerian universe, and obtain the distance–redshift relation. In Sect. 4, we use the Union2.1 compilation to derive the preferred direction of the universe. We find that it is obviously aligned with the dipole direction of the fine-structure constant. Finally, conclusions and remarks are given in Sect. 5.

2 Anisotropic universe

Finsler geometry is based on the so-called Finsler structure \(F\) defined on the tangent bundle of a manifold \(M\), with the property \(F(x,\lambda y)=\lambda F(x,y)\) for all \(\lambda >0\), where \(x\in M\) represents position and \(y\equiv \mathrm{d}x/\mathrm{d}\tau \) represents velocity. The Finslerian metric is given as [14]

$$\begin{aligned} g_{\mu \nu }\equiv \frac{\partial }{\partial y^\mu }\frac{\partial }{\partial y^\nu }\left( \frac{1}{2}F^2\right) \!. \end{aligned}$$
(1)

In physics, the Finsler structure \(F\) is not positive-definite at every point of Finsler manifold. We focus on investigating Finsler spacetime with a Lorentz signature. A positive, zero, and negative \(F\) correspond to time-like, null, and space-like curves, respectively. For massless particles, the stipulation is \(F=0\). The Finslerian metric reduces to Riemannian metric, if \(F^2\) is quadratic in \(y\). One non-Riemannian Finsler spacetime is the Randers spacetime [50]. It is given as

$$\begin{aligned} F_\mathrm{Ra}(x,y)\equiv \alpha (x,y)+\beta (x,y), \end{aligned}$$
(2)

where

$$\begin{aligned} \alpha (x,y)\equiv & {} \sqrt{\tilde{a}_{\mu \nu }(x)y^\mu y^\nu },\end{aligned}$$
(3)
$$\begin{aligned} \beta (x,y)\equiv & {} \tilde{b}_\mu (x)y^\mu , \end{aligned}$$
(4)

and \(\tilde{a}_{ij}\) is a Riemannian metric. Throughout this paper, the indices are lowered and raised by \(g_{\mu \nu }\) and its inverse matrix \(g^{\mu \nu }\). The objects that are decorated with a tilde are lowered and raised by \(\tilde{a}_{\mu \nu }\) and its inverse matrix \(\tilde{a}^{\mu \nu }\).

In this paper, we propose the ansatz that the Finsler structure of the universe is of the form

$$\begin{aligned} F^2=y^ty^t-a^2(t)F_\mathrm{Ra}^2, \end{aligned}$$
(5)

where we require that the vector \(\tilde{b}_i\) in \(F_\mathrm{Ra}\) is of the form \(\tilde{b}_i=\{0,0,B\}\) and \(B\) is a constant. Here, the Riemannian metric \(\tilde{a}_{ij}\) of the Randers space \(F_\mathrm{Ra}\) is set to be Euclidean, that is, \(\tilde{a}_{ij}=\delta _{ij}\). Thus the Finslerian universe (5) returns to FRW spacetime while \(B=0\). The above requirement for \(\tilde{b}_i\) and \(\tilde{a}_{ij}\) implies that the spatial part of the universe \(F_\mathrm{Ra}\) is a flat Finsler space, since all types of Finslerian curvatures vanish for \(F_\mathrm{Ra}\). The Killing equations of Randers space \(F_\mathrm{Ra}\) are given as [16, 49]

$$\begin{aligned} L_V \alpha= & {} \tilde{a}_{\mu \nu ,\gamma }\tilde{V}^\gamma +\tilde{a}_{\gamma \nu }\tilde{V}^\gamma _{~,\mu }+\tilde{a}_{\gamma \mu }\tilde{V}^\gamma _{~,\nu }= 0,\end{aligned}$$
(6)
$$\begin{aligned} L_V \beta= & {} \tilde{V}^\mu \frac{\partial \tilde{b}_\nu }{\partial x^\mu }+\tilde{b}_\mu \frac{\partial \tilde{V}^\mu }{\partial x^\nu }= 0, \end{aligned}$$
(7)

where \(L_V\) is the Lie derivative along the Killing vector \(V\) and the comma denotes the derivative with respect to \(x^\mu \). Noticing that the vector \(\tilde{b}_i\) is parallel to the \(z\)-axis, we find from the Killing equations (6), (7) that there are four independent Killing vectors in Randers space \(F_\mathrm{Ra}\). Three of them represent the translation symmetry, and the remaining one represents the rotational symmetry in the \(x\)–\(y\) plane. It means that the rotational symmetries in the \(x\)–\(z\) and \(y\)–\(z\) planes are broken. This fact means that the Finslerian universe (5) is anisotropic.

To derive the relation between luminosity distance and redshift, first we need investigate the redshift of a photon in Finslerian universe (5). The redshift of a photon can be derived from the geodesic equation. The geodesic equation for Finsler manifold is given as [14]

$$\begin{aligned} \frac{\mathrm{d}^2x^\mu }{\mathrm{d}\tau ^2}+2G^\mu =0, \end{aligned}$$
(8)

where

$$\begin{aligned} G^\mu =\frac{1}{4}g^{\mu \nu }\left( \frac{\partial ^2 F^2}{\partial x^\lambda \partial y^\nu }y^\lambda -\frac{\partial F^2}{\partial x^\nu }\right) \end{aligned}$$
(9)

is called geodesic spray coefficients. It can be proved from the geodesic equation (8) that the Finsler structure \(F\) is a constant along the geodesic. Plugging the Finsler structure (5) into Eq. (9), we obtain

$$\begin{aligned} G^0= & {} \frac{1}{2}a\dot{a}F_\mathrm{Ra}^2,\end{aligned}$$
(10)
$$\begin{aligned} G^i= & {} Hy^iy^0, \end{aligned}$$
(11)

where the dot denotes the derivative with respect to time and \(H\equiv \dot{a}/a\) is the Hubble parameter. Then the geodesic equations in Finsler universe (5) are given as

$$\begin{aligned}&\frac{\mathrm{d}^2t}{\mathrm{d}\tau ^2}+a\dot{a}F_\mathrm{Ra}^2=0,\end{aligned}$$
(12)
$$\begin{aligned}&\frac{\mathrm{d}^2x^i}{\mathrm{d}\tau ^2}+2H\frac{\mathrm{d}x^i}{\mathrm{d}\tau }\frac{\mathrm{d}x^0}{\mathrm{d}\tau }=0. \end{aligned}$$
(13)

In Finsler spacetime the null condition of the photon is given as \(F=0\). It is of the form

$$\begin{aligned} \left( \frac{\mathrm{d}t}{\mathrm{d}\tau }\right) ^2-a^2F^2_\mathrm{Ra}=0. \end{aligned}$$
(14)

Plugging the null condition (14) into the geodesic equation (12), we obtain the solution

$$\begin{aligned} \frac{\mathrm{d}t}{\mathrm{d}\tau }\propto \frac{1}{a}. \end{aligned}$$
(15)

It shows that the formula of the redshift \(z\) is

$$\begin{aligned} 1+z=\frac{c_0}{ca}, \end{aligned}$$
(16)

where \(c\) is the speed of light and the subscript zero denotes the quantities given at the present epoch.

The recent Michelson–Morley experiment carried through by Müller et al. [51] gives a precise limit on Lorentz invariance violation. Their experiment shows that the change of resonance frequencies of the optical resonators is of this magnitude \(|\delta \omega /\omega |\sim 10^{-16}\). It means that the Minkowski spacetime describes well the inertial system on the earth. Thus, we must require no variation of the speed of light at the present epoch. In Finslerian universe, the local inertial system at large cosmological scale is built by the flat Finsler spacetime, namely,

$$\begin{aligned} F^2_f=y^ty^t-F_\mathrm{Ra}^2. \end{aligned}$$
(17)

Thus, the radial speed of light at large cosmological scale can be derived from \(F_f=0\). It is of the form

$$\begin{aligned} c_r=\frac{1}{1+B\cos \theta }, \end{aligned}$$
(18)

where \(\theta \) denotes the angle with respect to the \(z\)-axis. Then, plugging Eq. (18) into Eq. (16), and noticing \(c_{r0}=1\), we obtain

$$\begin{aligned} 1+z=\frac{1+B\cos \theta }{a}. \end{aligned}$$
(19)

A direct deduction shows that the variation of the speed of light is the variation of the fine-structure constant. By making use of Eq. (18), we obtain the variation of the fine-structure constant,

$$\begin{aligned} \frac{\varDelta \alpha _e}{\alpha _e}=-\frac{\varDelta c_r}{c_{r0}}=B\cos \theta +O(b^2). \end{aligned}$$
(20)

Here, we suppose that the Finslerian parameter \(B\) is a small quantity. Equation (20) tells us that \(\varDelta \alpha _e/\alpha _e\) has a dipole distribution at the cosmological scale, which is compatible with the observations on quasar absorption spectra [11, 12].

3 Gravitational field equation in Finslerian universe

In Finsler geometry, there is a geometrical invariant quantity, i.e., Ricci scalar. It is of the form [14]

$$\begin{aligned} \hbox {Ric}\equiv R^\mu _\mu= & {} \frac{1}{F^2}\left( 2\frac{\partial G^\mu }{\partial x^\mu }-y^\lambda \frac{\partial ^2 G^\mu }{\partial x^\lambda \partial y^\mu }\right. \nonumber \\&\left. +2G^\lambda \frac{\partial ^2 G^\mu }{\partial y^\lambda \partial y^\mu }-\frac{\partial G^\mu }{\partial y^\lambda }\frac{\partial G^\lambda }{\partial y^\mu }\right) , \end{aligned}$$
(21)

where \(R^\mu _{~\nu }=R^{~\mu }_{\lambda ~\nu \rho }y^\lambda y^\rho /F^2\). Though \(R^{~\mu }_{\lambda ~\nu \rho }\) depends on connections, \(R^\mu _{~\nu }\) does not [14]. The Ricci scalar only depends on the Finsler structure \(F\) and is insensitive to the connections. Plugging the geodesic coefficients (10), (11) into the formula of the Ricci scalar (21), we obtain

$$\begin{aligned} F^2\hbox {Ric}=-3\frac{\ddot{a}}{a}y^ty^t+(a\ddot{a}+2\dot{a}^2)F^2_\mathrm{Ra}. \end{aligned}$$
(22)

Here, we define the modified Einstein tensor in Finsler spacetime as

$$\begin{aligned} G^\mu _\nu \equiv \hbox {Ric}^\mu _\nu -\frac{1}{2}\delta ^\mu _\nu S, \end{aligned}$$
(23)

where the Ricci tensor is defined as [52]

$$\begin{aligned} \hbox {Ric}_{\mu \nu }=\frac{\partial ^2\left( \frac{1}{2}F^2 \hbox {Ric}\right) }{\partial y^\mu \partial y^\nu }, \end{aligned}$$
(24)

and the scalar curvature in Finsler spacetime is given as \(S=g^{\mu \nu }\hbox {Ric}_{\mu \nu }\). Plugging the equation of the Ricci scalar (22) into Eq. (23), we obtain

$$\begin{aligned} G^t_t= & {} 3H^2,\end{aligned}$$
(25)
$$\begin{aligned} G^i_j= & {} \left( \frac{2\ddot{a}}{a}+H^2\right) \delta ^i_j. \end{aligned}$$
(26)

Following a similar approach to Ref. [49], in order to construct a self-consistent gravitational field equation in Finsler spacetime (5), we investigate the covariant conservative properties of the modified Einstein tensor \(G^\mu _\nu \). The covariant derivative of \(G^\mu _\nu \) in Finsler spacetime is given as [14]

$$\begin{aligned} G^\mu _{\nu ~|\mu }=\frac{\delta }{\delta x^\mu }G^\mu _\nu +\varGamma ^\mu _{\mu \rho }G^\rho _\nu -\varGamma ^\rho _{\mu \nu }G^\mu _\rho , \end{aligned}$$
(27)

where

$$\begin{aligned} \frac{\delta }{\delta x^\mu }=\frac{\partial }{\partial x^\mu }-\frac{\partial G^\rho }{\partial y^\mu }\frac{\partial }{\partial y^\rho }, \end{aligned}$$
(28)

and \(\varGamma ^\mu _{\mu \rho }\) is the Chern connection. Here, we have used ‘\(|\)’ to denote the covariant derivative. The Chern connection can be expressed in terms of the geodesic spray coefficients \(G^\mu \) and the Cartan connection, \(A_{\lambda \mu \nu }\equiv \frac{F}{4}\frac{\partial }{\partial y^\lambda }\frac{\partial }{\partial y^\mu }\frac{\partial }{\partial y^\nu }(F^2)\) [14],

$$\begin{aligned} \varGamma ^\rho _{\mu \nu }=\frac{\partial ^2 G^\rho }{\partial y^\mu \partial y^\nu }-A^\rho _{\mu \nu |\kappa }\frac{y^\kappa }{F}. \end{aligned}$$
(29)

Noticing that the modified Einstein tensor \(G^\mu _\nu \) does not have \(y\)-dependence, and the Cartan tensor is \(A^\rho _{\mu \nu }=A^i_{jk}\) (index \(i,j,k\) run over \(\theta ,\varphi \)), one can easily see that the Chern connection \(\varGamma ^\rho _{\mu \nu }\) equals the Christoffel connection that is deduced from the FRW metric if \(\varGamma ^\rho _{\mu \nu }\ne \varGamma ^i_{jk}\). By making use of this property and the formula of the geodesic spray (10), (11), we find that

$$\begin{aligned} G^\mu _{\nu ~|\mu }=0. \end{aligned}$$
(30)

Now, we have proved that the modified Einstein tensor is conserved in Finsler spacetime. Then, in the spirit of general relativity, we propose that the gravitational field equation in the given Finsler spacetime (5) should be of the form

$$\begin{aligned} G^\mu _\nu =8\pi G T^\mu _\nu , \end{aligned}$$
(31)

where \(T^\mu _\nu \) is the energy-momentum tensor. The volume of Finsler space [53] is generally different from the one of Riemann geometry. However, in terms of the Busemann–Hausdorff volume form, the volume of a closed Randers–Finsler surface is the same as the unit Riemannian sphere [53]. This is why we have used \(\pi \) in the field equation (31).

Since the modified Einstein tensor \(G^\mu _\nu \) only depends on \(x^\mu \), the gravitational field equation (31) requires that the energy-momentum tensor \(T^\mu _\nu \) depends on \(x^\mu \) and contains diagonal components only. Therefore, we set \(T^\mu _{\nu }\) to have the form

$$\begin{aligned} T^\mu _\nu =\mathrm{diag}(\rho ,-p,-p,-p), \end{aligned}$$
(32)

where \(\rho =\rho (x^\mu )\) and \(p=p(x^\mu )\) are the energy density and the pressure density of universe, respectively. Then the gravitational field equation (31) can be written as

$$\begin{aligned}&3H^2=8\pi G\rho ,\end{aligned}$$
(33)
$$\begin{aligned}&\frac{2\ddot{a}}{a}+H^2=-8\pi G p. \end{aligned}$$
(34)

The covariant conservation of the energy-momentum tensor \(T^\mu _{\nu ~|\mu }\) gives

$$\begin{aligned} \dot{\rho }+3H(\rho +p)=0. \end{aligned}$$
(35)

Combining Eqs. (33), (35), we obtain

$$\begin{aligned} H^2=H_0^2(\varOmega _{m0}a^{-3}+\varOmega _\varLambda ), \end{aligned}$$
(36)

where \(H_0\) is the Hubble constant, \(\varOmega _{\varLambda }\equiv 8\pi G\rho _{\varLambda }/(3H_0^2)\) and \(\varOmega _{m0}\equiv 8\pi G\rho _{m0}/(3H_0^2)\).

4 Observational constraints on Finslerian universe

Here we focus on using the Union2.1 SnIa data [5] to study the preferred direction of the universe and constrain the magnitude of the Finslerian parameter \(B\). By making use of Eqs. (14), (19), and (36), the luminosity distance in the Finslerian universe is given as

$$\begin{aligned} d_L= & {} (1+z)r=\frac{1+z}{H_0}\int _0^z\nonumber \\&\times \frac{\mathrm{d}z}{\sqrt{\varOmega _{m0}(1+z)^3(1-3B\cos \theta )+1-\varOmega _{m0}}}, \end{aligned}$$
(37)

where \(r=\sqrt{x^2+y^2+z^2}\) is the radial distance. To find the preferred direction in the Finslerian universe, we perform a least-\(\chi ^2\) fit to the Union2.1 SnIa data

$$\begin{aligned} \chi ^2\equiv \sum \frac{(\mu _{\mathrm{th}}-\mu _{\mathrm{obs}})^2}{\sigma _\mu ^2}, \end{aligned}$$
(38)

where \(\mu _{\mathrm{th}}\) is the theoretical distance modulus given by

$$\begin{aligned} \mu _{\mathrm{th}}=5\log _{10}\frac{d_L}{\mathrm{Mpc}}+25. \end{aligned}$$
(39)

\(\mu _\mathrm{obs}\) and \(\sigma _\mu \), given by the Union2.1 SnIa data, denote the observed values of the distance modulus and the measurement errors, respectively. The least-\(\chi ^2\) fit of Eq. (37) to the Union2.1 data shows that the preferred direction locates at \((l,b)=(314.6^\circ \pm 20.3^\circ ,-11.5^\circ \pm 12.1^\circ )\), and the magnitude of anisotropy \(B=(-3.60\, \pm \,1.66)\times 10^{-2}\). The preferred direction is consistent with the dipole direction derived by Ref. [13]. Before using our model to fit the Union2.1 SnIa data, we have fixed the Hubble constant \(H_0\) and \(\varOmega _{m0}\) to be \(H_0=70.0~\mathrm{km}~\mathrm{s}^{-1}~\mathrm{Mpc}^{-1}\) and \(\varOmega _{m0}=0.278\), which are derived by fitting the Union2.1 data to the standard \(\varLambda \)CDM model.

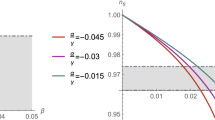
In the Finslerian universe (5), the fine-structure constant has a dipole structure [see Eq. (20) for details]. We fit the data of the quasar absorption spectra [12] obtained by the Very Large Telescope (VLT) and the Keck Observatory to Eq. (20), and we find the magnitude of the dipole to be \(B=(0.97\pm 0.21)\times 10^{-5}\), pointing toward \((l,b)=(333.2^\circ \pm 8.8^\circ ,-12.7^\circ \pm 6.3^\circ )\) in the galactic coordinate system. We plot the preferred direction of the Union2.1 sample and the dipole direction of the fine-structure constant in the galactic coordinate system in Fig. 1. We can see that they are consistent within \(1\sigma \) uncertainty. The angular separation between the two directions is about \(18.2^\circ \).

Fig. 1
figure 1

The preferred directions in the galactic coordinate system. The red point locates at \((l,b)=(314.6^\circ \pm 20.3^\circ ,-11.5^\circ \pm 12.1^\circ )\), which is obtained by fixing the parameters \(\varOmega _{m0}=0.278\) and \(H_0=70.0~\mathrm{km}~\mathrm{s}^{-1}~\mathrm{Mpc}^{-1}\) and doing the least-\(\chi ^2\) fit to the Union2.1 data for formula (37). The blue point locates at \((l,b)=(333.2^\circ \pm 8.8^\circ ,-12.7^\circ \pm 6.3^\circ )\), which is obtained by the least-\(\chi ^2\) fit to the data of the fine-structure constant. The contours enclose 68 % confidence regions for the preferred directions. The angular separation between the two preferred directions is about \(18.2^\circ \)

Full size image

5 Conclusions and remarks

In this paper, we have suggested that the universe is Finslerian. The Finslerian universe (5) breaks the rotational symmetry in the \(x\)–\(z\) and \(y\)–\(z\) planes, and it modifies the speed of light at a large cosmological scale. The preferred direction of the Union2.1 SnIa sample and the dipole structure of the fine-structure constant are naturally given in a Finslerian universe. Equations (20) and (37) show that the preferred directions of cosmic accelerating expansion and fine-structure constant both locate at the same direction. This fact is compatible with our numerical results. By applying Eq. (37) to the Union2.1 SnIa data, we found a preferred direction \((l,b)=(314.6^\circ \pm 20.3^\circ ,-11.5^\circ \pm 12.1^\circ )\). By applying Eq. (20) to the data of quasar absorption spectra, we found a preferred direction \((l,b)=(333.2^\circ \pm 8.8^\circ ,-12.7^\circ \pm 6.3^\circ )\). The angular separation between the two preferred directions is about \(18.2^\circ \), which means that the two directions are compatible within \(1\sigma \) uncertainty. However, our numerical results show that the anisotropic magnitude that corresponds to Union2.1 SnIa data and the data of quasar absorption spectra are different. This fact contradicts the prediction of the Finslerian universe, which requires that the absolute values of magnitude of the anisotropy should be the same. If the universe is Finslerian, such a contradiction may be attributed to two reasons. One reason is that the Finslerian parameter \(B\) should be a function of the redshift, since the ranges of the redshifts of the two observational datasets are different. The other reason is that the Union2.1 SnIa data are not accurate enough. Our numerical results for the magnitude of Finslerian parameter \(B\) show that the statistical significance of Union2.1 SnIa data is about \(2\sigma \) confidence level, while the data of the fine-structure constant is about \(4\sigma \) confidence level. Thus, further astronomical observations are needed in order to enhance the statistical significance in the future.