Effective spectrum width of the synchrotron radiation

Abstract

For an exact quantitative description of spectral properties of synchrotron radiation (SR), the concept of effective width of the spectrum is introduced. In the most interesting case, which corresponds to the ultrarelativistic limit of SR, the effective width of the spectrum is calculated for the polarization components, and new physically important quantitative information on the structure of spectral distributions is obtained. For the first time, the spectral distribution for the circular polarization component of the SR for the upper half-space is obtained within classical theory.

1 Introduction

The theory of synchrotron radiation (SR) is currently a quite well-developed branch of theoretical physics. Its basic elements have been stated in books (e.g., [1–5]) and numerous articles. As one of the most physically important features of SR, one should mention a high polarization degree of radiation and a unique structure of spectral distribution in the ultrarelativistic limit. All the theoretically predicted properties of SR have been confirmed experimentally.

The development of the SR theory makes it possible not only to predict qualitatively the peculiar features of radiation, but also to propose exact quantitative characteristics of physically important properties.

For instance, the high polarization degree of SR was predicted qualitatively by theory more than half a century ago (see, e.g., [1]), and the linear polarization was given exact quantitative characteristics; however, it was not until much later that it proved to be possible to obtain exact quantitative characteristics for circular polarization [6, 7].

In this paper, we propose new exact quantitative characteristics of the SR spectral distribution, the effective width of the spectrum. We demonstrate how to calculate this quantity theoretically in the most interesting case, which corresponds to the ultrarelativistic limit of SR, and what physically important information can be obtained using this quantity. We demonstrate that for spectral distributions of SR the well-known characteristics - the half-width of the spectrum is less informative than the proposed effective width. We place in the Appendix all necessary formulas for our purposes that describe the spectral-angular distribution of the SR. Our consideration is performed in the framework of the classical theory of SR. It is well known that such a theory is valid with high accuracy for accessible parameters of the electron beam in modern accelerators and storage rings. However, for SR in cosmic space quantum effects can be quite essential (see. Ref. [8]) and thus can significantly change classical results (which may be the subject of a separate study).

2 The effective width of the spectrum of SR polarization components

Let us define the effective width of the spectrum $\Lambda _{s}(\beta )$ as the minimum spectral range that accounts for at least half of the total radiated power of a given polarization component,

$$\begin{aligned} \Lambda _{s}(\beta )=\nu _{s}^{(2)}(\beta )-\nu _{s}^{(1)}(\beta )+1. \end{aligned}$$

(1)

The harmonics $\nu _{s}^{(1)}(\beta )$ and $\nu _{s}^{(2)}(\beta )$ determine the beginning and the end of this minimum spectral range and are determined as follows:

Let us introduce the quantities

$$\begin{aligned} \widetilde{\Phi }_{s}(\beta ;\,\nu ^{(1)},\,\nu ^{(2)})=\sum _{\nu =\nu ^{(1)}}^{ \nu ^{(2)}}F_{s}^{(+)}(\beta ;\,\nu ), 1\leqslant \nu ^{(1)}\leqslant \nu ^{(2)}\leqslant \infty . \nonumber \\ \end{aligned}$$

(2)

It is obvious that the following relations hold true:

$$\begin{aligned} \Phi _{s}^{(+)}(\beta )= & {} \widetilde{\Phi }_{s}(\beta ;\,\nu ^{(1)}=1,\,\nu ^{(2)}=\infty );\nonumber \\&\times \Phi _{s}^{(+)}(\beta )>\widetilde{\Phi }_{s}(\beta ;\,\nu ^{(1)}\geqslant 1,\,\nu ^{(2)}<\infty ). \end{aligned}$$

(3)

Let us consider a set of such $\nu ^{(1)},\,\,\nu ^{(2)}\,(1\leqslant \nu ^{(1)}\leqslant \nu ^{(2)}<\infty )$ that satisfy the inequality

$$\begin{aligned} \widetilde{\Phi }_{s}(\beta ;\,\nu ^{(1)},\,\nu ^{(2)})\geqslant \frac{1}{2} \Phi _{s}^{(+)}(\beta ). \end{aligned}$$

(4)

Obviously, such $\nu ^{(1)},\,\nu ^{(2)}$ do exist for any $\beta$ (for instance, the case $\nu ^{(1)}=1$ provides the existence of such a finite $\nu ^{(2)}$). It is equally obvious that the condition (4) alone is generally insufficient to determine such a pair of values $\nu ^{(1)},\,\nu ^{(2)}$. Let us choose such $\nu _{s}^{(1)}(\beta ),\,\, \nu _{s}^{(2)}(\beta )$ that the fulfillment of (4) implies that the difference $\nu _{s}^{(2)}(\beta )-\nu _{s}^{(1)}(\beta )$ is minimal, and the following non-negative value is also minimal:

$$\begin{aligned} \widetilde{\Phi }_{s}(\beta ;\,\nu _{s}^{(1)}(\beta ),\,\nu _{s}^{(2)}(\beta ))- \frac{1}{2}\Phi _{s}^{(+)}(\beta )\geqslant 0. \end{aligned}$$

(5)

A definition equivalent to the above for the effective width of the spectrum can be given using the concept of the partial contribution $P_{s}(\beta ;\nu ),$

$$\begin{aligned} P_{s}(\beta ;\nu )=\frac{F_{s}^{(+)}(\beta ;\,\nu )}{\Phi _{s}^{(+)}(\beta )}, \end{aligned}$$

(6)

of separate harmonics of the spectrum, introduced in [8]. Then (30 ) implies the property

$$\begin{aligned} \sum _{\nu =1}^{\infty }P_{s}(\beta ;\nu )=1. \end{aligned}$$

(7)

Let us choose $\nu _{s}^{(1)}(\beta )$ and $\nu _{s}^{(2)}(\beta )$ such that at the minimum difference $\nu _{s}^{(2)}(\beta )-\nu _{s}^{(1)}(\beta )$ the following non-negative quantity is minimal:

$$\begin{aligned} \sum _{\nu =\nu _{s}^{(1)}(\beta )}^{\nu _{s}^{(2)}(\beta )}P_{s}(\beta ;\nu )- \frac{1}{2}\geqslant 0. \end{aligned}$$

(8)

Introducing $\Lambda _{s}(\beta )$ in accordance with (1), we arrive at the following equivalent definition: the effective width of the spectrum is the minimum spectral range at which the sum of the partial contributions of separate harmonics is no less than 1 / 2.

From a practical point of view, the most interesting case is presented by the ultrarelativistic limit ($\beta \approx 1$, which is equivalent to $\gamma \gg 1$) of SR. In this case, a big part of the study of the effective width, as well as the study of other physically interesting quantitative characteristics of the spectral distribution of SR polarization components, can be done analytically.

3 The ultrarelativistic case

At the higher energies of a charge (which implies the condition $\gamma \gg 1$), we can use the well-known [1–5] approximations of the Bessel functions by using the MacDonald functions (Bessel functions of 2nd kind) and replacing the summation over $\nu$ by integration. As a result, the expressions (30) for $\Phi _{s}^{(+)}(\beta \approx 1)=\Phi _{s}^{(+)}$ can be written in the following form

$$\begin{aligned} \Phi _{s}^{(+)}=\int _{0}^{\infty }F_{s}^{(+)}(y)\mathrm{d}y,\ \ y=\frac{2\nu }{ 3\gamma ^{3}}, \end{aligned}$$

(9)

where the spectral densities $F_{s}^{(+)}(y)$ (32) take the form

$$\begin{aligned} F_{2}^{(+)}(y)&=\frac{9\sqrt{3}}{32\pi }\,y\left[ 3K_{2/3}(y)-\int _{y}^{\infty }K_{1/3}(x)\mathrm{d}x\right] , \nonumber \\ F_{3}^{(+)}(y)&=\frac{9\sqrt{3}}{32\pi }\,y\left[ K_{2/3}(y)-\int _{y}^{\infty }K_{1/3}(x)\mathrm{d}x\right] , \nonumber \\ F_{0}^{(+)}(y)&=F_{2}^{(+)}(y)+F_{3}^{(+)}(y),\ \ F_{\pm 1}^{(+)}(y)\nonumber \\&= \frac{1}{2}F_{0}^{(+)}(y)\pm \frac{9}{16\pi ^{2}}\,y\,K_{1/3}^{2}\left( \frac{y }{2}\right) . \end{aligned}$$

(10)

Here, $K_{1/3}(x)$ and $K_{2/3}(x)$ are MacDonald functions (Bessel functions of 2nd kind).

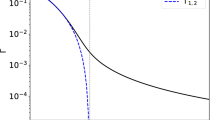
The functions $F_{s}^{(+)}(y)$ are plotted in Fig. 1.

Fig. 1

Spectral distribution for $F_{s}^{(+)}(y)$

Let us also introduce the function $\Phi _{s}^{(+)}(y)$

$$\begin{aligned} \Phi _{s}^{(+)}(y)=\int _{0}^{y}F_{s}^{(+)}(x)\mathrm{d}x;\ \ \Phi _{s}^{(+)}=\Phi _{s}^{(+)}(y=\infty ). \end{aligned}$$

(11)

The values of $\Phi _{s}^{(+)}$, according to (33) and taking account of (34), are known exactly:

$$\begin{aligned} \Phi _{2}^{(+)}&=\frac{7}{16},\ \ \Phi _{3}^{(+)}=\frac{1}{16},\ \ \Phi _{0}^{(+)}=\frac{1}{2}, \nonumber \\ \Phi _{\pm 1}^{(+)}&=\frac{1}{4}\left( 1\pm \frac{\sqrt{3}}{\pi }\right) \approx \frac{1}{2}\left\{ \begin{array}{c} 0,7756644 \\ 0,2243356 \end{array} \right. =\left\{ \begin{array}{c} 0,3878322 \\ 0,1121678 \end{array} \right. . \end{aligned}$$

(12)

In particular, it follows from (12), that, in the upper half-space, 77.6 % of the radiated power is attributed to right circular polarization and 22.4 % is attributed to left circular polarization.

The functions $\Phi _{s}^{(+)}(y)$ can be written down as follows:

$$\begin{aligned} \Phi _{2}^{(+)}(y)= & {} \frac{9\sqrt{3}}{32\pi }\,\left[ 3J_{1}(y)+J_{2}(y)- \frac{\pi \,y^{2}}{2\sqrt{3}}\right] ,\nonumber \\&\Phi _{3}^{(+)}(y)=\Phi _{2}^{(+)}(y)+ \frac{9\sqrt{3}}{16\pi }\,J_{1}(y), \nonumber \\&\Phi _{0}^{(+)}(y) =\Phi _{2}^{(+)}(y)+\Phi _{3}^{(+)}(y),\ \Phi _{\pm 1}^{(+)}(y)\nonumber \\= & {} \frac{1}{2}\Phi _{0}^{(+)}(y)\pm \frac{3}{8\pi ^{2}}\,J_{3}\left( \frac{y}{2}\right) \pm \frac{\sqrt{3}}{4\pi }, \end{aligned}$$

(13)

where the following notations are used

$$\begin{aligned} J_{1}(y)= & {} \frac{2}{3}\int _{0}^{y}K_{1/3}(x)\mathrm{d}x-yK_{1/3}(y), \nonumber \\ J_{2}(y)= & {} \left( \frac{y^{2}}{2}-\frac{4}{9}\right) \int _{0}^{y}K_{1/3}(x)\mathrm{d}x+\frac{2}{3}yK_{1/3}(y)\nonumber \\&+\frac{y^{2}}{2}K_{2/3}(y), \nonumber \\ J_{3}(y)= & {} 3y^{2}\left[ K_{1/3}^{2}(y)-K_{2/3}^{2}(y)\right] -2yK_{1/3}(y)K_{2/3}(y). \nonumber \\ \end{aligned}$$

(14)

3.1 The effective width of the spectrum in the ultrarelativistic limit

According to the given above definition, to determine the effective width of the spectrum in the ultrarelativistic limit, one has to find such $y_{s}^{(1)}$ and $y_{s}^{(2)}>y_{s}^{(1)}$ that

$$\begin{aligned} \int _{y_{s}^{(1)}}^{y_{s}^{(2)}}F_{s}^{(+)}(y)\mathrm{d}y=\frac{1}{2} \Phi _{s}^{(+)}, \end{aligned}$$

(15)

and given this, the differences $y_{s}^{(2)}-y_{s}^{(1)}=\Delta _{s}>0$ must be minimal.

It is convenient to use Eq. (15) to determine first $y_{s}^{(2)}$ as a function of $y_{s}^{(1)}$, or equivalently, to determine $\Delta _{s}$ as a function $y_{s}^{(1)}$. Let us write

$$\begin{aligned} y_{s}^{(2)}\left( y_{s}^{(1)}\right) =y_{s}^{(1)}+\Delta _{s}\left( y_{s}^{(1)}\right) . \end{aligned}$$

This implies the following relation:

$$\begin{aligned} y_{s}^{(2)\,^{\prime }}\equiv \frac{\mathrm{d}y_{s}^{(2)}\left( y_{s}^{(1)}\right) }{\mathrm{d}y_{s}^{(1)}}=1+\Delta _{s}^{\prime },\ \ \Delta _{s}^{\prime }\equiv \frac{\mathrm{d}\Delta _{s}\left( y_{s}^{(1)}\right) }{\mathrm{d}y_{s}^{(1)}}. \end{aligned}$$

(16)

Taking (16) into account, we differentiate (15) with respect to $y_{s}^{(1)}$ to obtain

$$\begin{aligned} \left( 1+\Delta _{s}^{\prime }\right) F_{s}^{(+)}\left( y_{s}^{(2)}\right) -F_{s}^{(+)}\left( y_{s}^{(1)}\right) =0. \end{aligned}$$

(17)

However, we need to find such $y_{s}^{(1)}$ that $\Delta _{s}\left( y_{s}^{(1)}\right)$ is minimal, which implies that $\Delta _{s}^{\prime }=0$ at the required point. Finally, in accordance with

$$\begin{aligned} \int _{y_{s}^{(1)}}^{\,y_{s}^{(2)}}F_{s}^{(+)}(y)\mathrm{d}y=\Phi _{s}^{(+)}\left( y_{s}^{(2)}\right) -\Phi _{s}^{(+)}\left( y_{s}^{(1)}\right) , \end{aligned}$$

(18)

we arrive at the following set of equations for the quantities $y_{s}^{(1)}$ and $y_{s}^{(2)}$:

$$\begin{aligned}&\Phi _{s}^{(+)}\left( y_{s}^{(2)}\right) -\Phi _{s}^{(+)}\left( y_{s}^{(1)}\right) =\frac{1}{2}\Phi _{s}^{(+)},\nonumber \\&F_{s}^{(+)}\left( y_{s}^{(2)}\right) =F_{s}^{(+)}\left( y_{s}^{(1)}\right) ,\ \ y_{s}^{(2)}>y_{s}^{(1)}, \end{aligned}$$

(19)

which allows one to determine them uniquely. Since, in accordance with (9), the relation $2\nu =3y\gamma ^{3}$ holds true, we obtain in the ultrarelativistic limit

$$\begin{aligned}&\nu _{s}^{(1)}(\beta )=a_{s}^{(1)}\gamma ^{3},\ \ \nu _{s}^{(2)}(\beta )=a_{s}^{(2)}\gamma ^{3}, \nonumber \\&\Lambda _{s}(\beta )=b_{s}\gamma ^{3},\ \ b_{s}=a_{s}^{(2)}-a_{s}^{(1)},\ \ a_{s}^{(k)}=\frac{3}{2}y_{s}^{(k)}. \end{aligned}$$

(20)

The distribution of the harmonics $\nu _{s}^{(1)}(\beta )$ and $\nu _{s}^{(2)}(\beta )$ and the quantities $\Lambda _{s}(\beta )$ follows exactly the same order. The effective width of the spectrum $\Lambda _{s}(\beta )$ is different for different polarizations, for instance, the ratio of the largest quantity $\Lambda _{-1}(\beta )$ to the smallest quantity $\Lambda _{3}(\beta )$ is $\sim$ 1, 76.

For each type of polarization (each s) the frequencies $\nu <\nu _{s}^{(max)}$ will be referred to as low, and the frequencies $\nu >\nu _{s}^{(max)}$ will be referred to as high. It is obvious that the portion $r_{s}^{(1)}$ of the effective width of the spectrum which corresponds to the low frequencies is given by

$$\begin{aligned} r_{s}^{(1)}=\frac{\nu _{s}^{(max)}(\beta )-\nu _{s}^{(1)}(\beta )}{ \nu _{s}^{(2)}(\beta )-\nu _{s}^{(1)}(\beta )}=\frac{a_{s}^{(max)}-a_{s}^{(1)}}{ b_{s}}\,. \end{aligned}$$

(21)

Table 1 Spectral emission characteristics in the ultra relativistic limit

3.2 Another characteristics of spectral distributions in the ultrarelativistic limit

The expressions (10) and (13) make it possible to obtain exact quantitative data for interesting physical characteristics of spectral distributions. These quantitative data are presented in the following Table 1.

Calculating the location of the maximum points $y_{s}^{(max)}$ of spectral distributions, one determines the frequencies that correspond to the maxima:

$$\begin{aligned} \nu _{s}^{(max)}(\beta )=a_{s}^{(max)}\gamma ^{3},\ \ a_{s}^{(max)}=\frac{3}{2 }y_{s}^{(max)}. \end{aligned}$$

(22)

The numerical values $a_{s}^{(max)}$ for $s=0,2,3$ are already known, whereas those for $s=\pm 1$ are presented here for the first time. The frequencies corresponding to the maxima are distributed in the following order for all values of $\beta$:

$$\begin{aligned} \nu _{3}^{(max)}(\beta )<\nu _{1}^{(max)}(\beta )<\nu _{0}^{(max)}(\beta )<\nu _{2}^{(max)}(\beta )<\nu _{-1}^{(max)}(\beta ). \end{aligned}$$

(23)

The quantity $100\,r_{s}^{(1)}$ determines the percentage of the effective width of the spectrum that is contributed by the low frequencies for each polarization. As we can see, the quantities $r_{s}^{(1)}$ are distributed in the order (23). It is quite interesting that the low frequencies contribute to a significantly smaller part of the effective width of the spectrum (from the maximum part $\sim$ 33.3 % for $s=-1$ to the minimum part $\sim$ 19.5 % for $s=3$), and therefore, most of the effective width of the spectrum is contributed by the high frequencies.

Let us introduce the quantities

$$\begin{aligned} \eta _{s}^{(k)}=\frac{\Phi _{s}^{(+)}(y_{s}^{(k)})}{\Phi _{s}^{(+)}}\,, \end{aligned}$$

(24)

that determine, for each s-component of SR polarization, the portion of power radiated by the interval of frequencies $0<\nu <\nu _{s}^{(k)}$ from the total power emitted at this polarization. It is obvious that the quantity $100\,\eta _{s}^{(k)}$ accordingly determines the percentage of power radiated at the spectral region $0<\nu <\nu _{s}^{(k)}$. The order of distribution of $\eta _{s}^{(k)}$ is identical with (23).

The numerical values $\eta _{s}^{(max)}$ provide convincing evidence of the fact that a substantially larger part of the radiated power at each component of polarization is contributed by the region of high frequencies (the maximum percentage of radiated power at low frequencies is $\sim$20.2 % for $s=-1$ and the minimum is $\sim$11.0 % for $s=3$, and therefore from $\sim$80 % to $\sim$90 % of the radiated power is contributed by the high frequencies).

The numerical values $\eta _{s}^{(1)}$ represent the portion of radiated power in the frequency range up to the beginning of the effective width of the spectrum. This portion is quite insignificant (the maximum percentage being $\sim$3.15 % for $s=-1$ and the minimum being $\sim$0.45 % for $s=3$).

The values $r_{s}^{(2)}=\eta _{s}^{(max)}-\eta _{s}^{(1)}$ determine the portion of radiated power at low frequencies that corresponds to the effective width of the spectrum (here, the maximum percentage of power radiated at low frequencies is $\sim$17.0 % for $s=-1$ and the minimum percentage is $\sim$10.6 % for $s=3$; there is an approximation $r_{s}^{(1)}\sim 2r_{s}^{(2)}$, which is physically quite justified, since the radiated powers are approximately proportional to the frequency ranges).

In optics one characterizes the profiles of spectral distributions by introducing the concept of the half-width of the spectrum. Such a quantity can also be introduced in the case under consideration.

Let us find some pairs of points $y_{s}^{(3)},y_{s}^{(4)}$ related by

$$\begin{aligned} F_{s}^{(+)}(y_{s}^{(3)})=F_{s}^{(+)}(y_{s}^{(4)})=\frac{1}{2} F_{s\,max}^{(+)},\ \ y_{s}^{(3)}<y_{s}^{(4)}, \end{aligned}$$

(25)

and calculate for these quantities characteristics similar to those considered above. In particular, the half-width of the spectrum $\Lambda _{s}^{1/2}(\beta )$ is determined by

$$\begin{aligned} \Lambda _{s}^{1/2}(\beta )=d_{s}\gamma ^{3}, d_{s}=a_{s}^{(4)}-a_{s}^{(3)}\,, a_{s}^{(k)}=\frac{3}{2}y_{s}^{(k)}, \end{aligned}$$

(26)

and the portion of radiated power that is attributed to the half-width is determined by the parameter $r_{s}^{(3)}=\eta _{s}^{(4)}-\eta _{s}^{(3)}$.

As we can see from the table, the half-width is attributed to the range from $\sim$60 to $\sim$70 % of radiated power, and the remaining part is radiated in the region of high frequencies (up to the beginning of the half-width, the radiated power is merely in the range of $\sim$0.16 to $\sim$0.61 %. Consequently, for spectral distributions of SR the concept of the half-width of the spectrum is less informative than the concept of the effective width of the spectrum that we have proposed in this article.

4 Brief summary

We give a new definition of the effective width for the SR spectrum and calculate the effective width for all polarization components of the SR in the ultra-relativistic limit. For the first time, the spectral distribution for the circular polarization component of the SR for the upper half-plane is obtained within classical theory. In addition, the relative radiation power emitted in some physically interesting spectral ranges is found.

Relevant equations of the synchrotron radiation theory

We present here some well-known in classical theory equations that describe the physical characteristics of synchrotron radiation (SR), see for example, the books [1–5].

The spectral-angular distribution of the radiation power of SR polarization components can be presented in the form

$$\begin{aligned} W_{s}=W\sum _{\nu =1}^{\infty }\int _{0}^{\pi }f_{s}(\beta ;\,\nu ,\,\theta )\sin \theta \mathrm{d}\theta . \end{aligned}$$

(27)

Here, $\theta$ is the angle between the direction of the magnetic field and the momentum of the field of radiation; $\nu$ is the number of emitted harmonics; the velocity of the charge in orbit is $v=c\beta$ , where c is the speed of light; W is the total radiated power of unpolarized radiation, which can be written down in the form

$$\begin{aligned} W=\frac{2}{3}\frac{ce^{2}}{R^{2}}(\gamma ^{2}-1)^{2}=\frac{2}{3}\frac{ e^{4}H^{2}(\gamma ^{2}-1)}{m_{0}^{2}c^{3}},\ \ \gamma =\frac{1}{\sqrt{ 1-\beta ^{2}}}, \nonumber \\ \end{aligned}$$

(28)

where e is the charge of the particle; R is the radius of the orbit; H is the strength of the magnetic field; $m_{0}$ is the rest mass of the charged particle; $\gamma$ is the relativistic factor. The index s serves to number the polarization components: $s=2$ corresponds to the $\sigma$ -component of linear polarization; $s=3$ corresponds to the $\pi$-component of linear polarization; $s=1$ stands for the right circular polarization; $s=-1$ stands for the left circular polarization; $s=0$ corresponds to the power of unpolarized radiation. The functions $f_{s}(\beta ;\,\nu ,\,\theta )$ have the form

$$\begin{aligned} f_{2}(\beta ;\,\nu ,\,\theta )&=\frac{3\nu ^{2}}{2\gamma ^{4}}J_{\nu }^{\prime }\,^{2}(x);\nonumber \\ f_{3}(\beta ;\,\nu ,\,\theta )&=\frac{3\nu ^{2}}{2\gamma ^{4}}\frac{ \cos ^{2}\theta }{\beta ^{2}\sin ^{2}\theta }J_{\nu }^{2}(x); \nonumber \\ f_{\pm 1}(\beta ;\,\nu ,\,\theta )&=\frac{3\nu ^{2}}{4\gamma ^{4}}\left[ J_{\nu }^{\prime }(x)\pm \varepsilon \frac{\cos \theta }{\beta \sin \theta }J_{\nu }(x) \right] ^{2};\nonumber \\&\qquad x=\nu \beta \sin \theta ;\ \ \varepsilon =-\frac{e}{|e|}; \nonumber \\ f_{0}(\beta ;\,\nu ,\,\theta )&=f_{2}(\beta ;\,\nu ,\,\theta )+f_{3}(\beta ;\,\nu ,\,\theta )\nonumber \\&=f_{1}(\beta ;\,\nu ,\,\theta )+f_{-1}(\beta ;\,\nu ,\,\theta )\,, \end{aligned}$$

(29)

where, $J_{\nu }(x)$ are the Bessel functions. The case of an electron corresponds to $\varepsilon =1$.

It is well known that in the region $0\leqslant \theta <\pi /2$ (this region will be called the upper half-space) the right circular polarization is dominant, whereas in the region $\pi /2<\theta \leqslant \pi$ (this region will be called the lower half-space) it is the left circular polarization that is dominant (exact quantitative characteristics of this property of SR were first obtained in [6, 7]). However, if in expression (27) one integrates over $\theta \ \ (0\leqslant \theta \leqslant \pi )$ then the differences in the spectral distribution of the right and left circular polarizations disappear. To identify these differences, we present the expressions (27) in the form

$$\begin{aligned}&W_{s}=W\left[ \Phi _{s}^{(+)}(\beta )+\Phi _{s}^{(-)}(\beta )\right] ;\nonumber \\&\Phi _{s}^{(+)}(\beta )=\sum _{\nu =1}^{\infty }F_{s}^{(+)}(\beta ;\,\nu ),\nonumber \\&\Phi _{s}^{(-)}(\beta )=\sum _{\nu =1}^{\infty }F_{s}^{(-)}(\beta ;\,\nu ); \nonumber \\&F_{s}^{(+)}(\beta ;\,\nu )=\int _{0}^{\pi /2}f_{s}(\beta ;\,\nu ,\,\theta )\sin \theta \mathrm{d}\theta ,\nonumber \\&F_{s}^{(-)}(\beta ;\,\nu )=\int _{\pi /2}^{\pi }f_{s}(\beta ;\,\nu ,\,\theta )\sin \theta \mathrm{d}\theta , \end{aligned}$$

(30)

and, besides, it is sufficient to study the properties of the functions $F_{s}^{(+)}(\beta ;\,\nu )$ (respectively, the properties of the functions $\Phi _{s}^{(+)}(\beta )$), since there exist the obvious relations

$$\begin{aligned} F_{s}^{(-)}(\beta ;\,\nu )&=F_{s}^{(+)}(\beta ;\nu ),\quad \Phi _{s}^{(-)}(\beta )=\Phi _{s}^{(+)}(\beta ),\quad s=0,\,2,\,3; \nonumber \\ F_{1}^{(-)}(\beta ;\,\nu )&=F_{-1}^{(+)}(\beta ;\,\nu ),\ \ \Phi _{1}^{(-)}(\beta )=\Phi _{-1}^{(+)}(\beta ), \nonumber \\ F_{-1}^{(-)}(\beta ;\,\nu )&=F_{1}^{(+)}(\beta ;\,\nu ),\ \ \Phi _{-1}^{(-)}(\beta )=\Phi _{1}^{(+)}(\beta ). \end{aligned}$$

(31)

Integration over $\theta$ in the upper half-space $0\leqslant \theta \leqslant \pi /2$ in (30) can be carried out exactly, which leads to the following expressions:

$$\begin{aligned} F_{2}^{(+)}(\beta ;\,\nu )= & {} \frac{3\nu }{4\,\gamma \,^{4}\beta ^{3}}\left[ 2\beta ^{2}J_{2\nu }^{\prime }(2\nu \beta )+\beta ^{2}\int _{0}^{2\nu \beta }J_{2\nu }(x)dx\right. \nonumber \\&\left. -2\nu \beta \int _{0}^{2\nu \beta }\frac{J_{2\nu }(x)}{x}dx\right] ,\nonumber \\ F_{3}^{(+)}(\beta ;\,\nu )= & {} \frac{3\nu }{4\,\gamma \,^{4}\beta ^{3}}\left[ 2\nu \beta \int _{0}^{2\nu \beta }\frac{J_{2\nu }(x)}{x}dx\right. \nonumber \\&\left. -\int _{0}^{2\nu \beta }J_{2\nu }(x)dx\right] , \nonumber \\ F_{0}^{(+)}(\beta ;\,\nu )= & {} F_{2}^{(+)}(\beta ;\,\nu )+F_{3}^{(+)}(\beta ;\,\nu )\nonumber \\= & {} \frac{3\nu }{4\,\gamma \,^{4}\beta ^{3}}\left[ 2\beta ^{2}J_{2\nu }^{\prime }(2\nu \beta )\right. \nonumber \\&\left. -(1-\beta ^{2})\int _{0}^{2\nu \beta }J_{2\nu }(x)dx\right] ,\nonumber \\ F_{\pm 1}^{(+)}(\beta ;\,\nu )= & {} \frac{1}{2}F_{0}^{(+)}(\beta ;\,\nu )\pm \frac{ 3\nu J\,_{\nu }^{2}(\nu \beta )}{4\,\gamma \,^{4}\beta ^{2}}. \end{aligned}$$

(32)

The sums over the harmonics $\nu$ in (30) can also be calculated exactly, which leads to the expressions

$$\begin{aligned}&\Phi _{2}^{(+)}(\beta )=\frac{6+\beta ^{2}}{16},\ \ \Phi _{3}^{(+)}(\beta )= \frac{2-\beta ^{2}}{16},\nonumber \\&\Phi _{0}^{(+)}(\beta )=\frac{1}{2},\ \ \Phi _{\pm 1}^{(+)}(\beta )=\frac{1}{4}\left[ 1\pm \frac{3}{4}\chi _{1}(\beta ) \right] . \end{aligned}$$

(33)

The function $\chi _{1}(\beta )$ introduced here has been defined and studied in [7]. In particular, the study of [7] demonstrated that in the segment $0\leqslant \beta \leqslant 1$ the function $\chi _{1}(\beta )$ is finite and decreases monotonously; at the ends of this segment, it takes the following values:

$$\begin{aligned} \chi _{1}(0)=1,\ \ \chi _{1}(1)=\frac{4}{\pi \sqrt{3}}. \end{aligned}$$

(34)