A search for a doubly-charged Higgs boson in pp collisions at $\sqrt{s} = 7 \ \mbox{TeV}$

Abstract

A search for a doubly-charged Higgs boson in pp collisions at $\sqrt{s} = 7 \ \mbox{TeV}$ is presented. The data correspond to an integrated luminosity of 4.9 fb⁻¹, collected by the CMS experiment at the LHC. The search is performed using events with three or more isolated charged leptons of any flavor, giving sensitivity to the decays of pair-produced triplet components Φ ⁺⁺ Φ ⁻⁻, and Φ ⁺⁺ Φ ⁻ from associated production. No excess is observed compared to the background prediction, and upper limits at the 95 % confidence level are set on the Φ ⁺⁺ production cross section, under specific assumptions on its branching fractions. Lower bounds on the Φ ⁺⁺ mass are reported, providing significantly more stringent constraints than previously published limits.

1 Introduction

The existence of non-zero neutrino masses may represent a signal of physics beyond the standard model (SM) [1]. The observation of a doubly-charged scalar particle would establish the type II seesaw mechanism as the most promising framework for generating neutrino masses [2]. The minimal type II seesaw model [3–6] is realized with an additional scalar field that is a triplet under SU(2)_L and carries U(1)_Y hypercharge Y=2. The triplet contains a doubly-charged component Φ ⁺⁺, a singly-charged component Φ ⁺ and a neutral component Φ ⁰. In this paper, the symbols Φ ⁺⁺ and Φ ⁺ are used to refer also to the charge conjugate states Φ ⁻⁻ and Φ ⁻. In the literature Δ and H have also been used. Our choice of the symbol Φ for the triplet components avoids possible confusion with the minimal supersymmetric model (MSSM) H ⁺ boson.

The Φ ⁺⁺ particle carries double electric charge, and decays to same-sign lepton pairs $\ell_{\alpha}^{+}\ell_{\beta}^{+}$ with flavor indices α,β, where α can be equal to or different from β. The Φ ⁺⁺ Yukawa coupling matrix Y _Φ is proportional to the light neutrino mass matrix. The measurement of the $\varPhi^{++}\to\ell_{\alpha}^{+}\ell_{\beta}^{+}$ branching fractions would therefore allow the neutrino mass generation mechanism to be tested [7]. In this scenario, measurements at the Large Hadron Collider (LHC) could shed light [8–11] on the absolute neutrino mass scale, the mass hierarchy, and the Majorana CP-violating phases. The latter are not measurable in current neutrino-oscillation experiments.

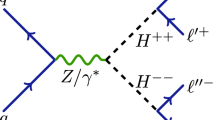
In this article the results of an inclusive search for a doubly-charged Higgs boson at the Compact Muon Solenoid (CMS) experiment are presented, based on a dataset corresponding to an integrated luminosity of 4.93±0.11 fb⁻¹. The dataset was collected in pp collisions at $\sqrt{s} = 7~\mbox{TeV}$ during the 2011 LHC running period. Both the pair-production process $\mathrm{p}\mathrm{p}\to \varPhi ^{++}\varPhi^{--}\to\ell_{\alpha}^{+}\ell_{\beta}^{+}\ell_{\gamma}^{-}\ell _{\delta}^{-}$ [12, 13] and the associated production process $\mathrm{p}\mathrm{p}\to\varPhi^{++}\varPhi ^{-}\to\ell _{\alpha}^{+}\ell_{\beta}^{+}\ell_{\gamma}^{-}\nu_{\delta}$ [14, 15] are studied. It is assumed that the Φ ⁺⁺ and Φ ⁺ are degenerate in mass. However, as the singly-charged component is not fully reconstructed, this requirement impacts only the cross section, as long as the mass splitting is such that cascade decays (e.g. Φ ⁺⁺→Φ ⁺W^+∗→Φ ⁰W^+∗W^+∗) are disfavored [16]. The relevant Feynman diagrams and production cross sections, calculated following [13], are presented in Figs. 1 and 2. The Φ ⁺⁺→W⁺W⁺ decays are assumed to be suppressed. In the framework of type II seesaw model [3–6], where the triplet is used to explain neutrino masses, this is a natural assumption: the decay width to the W⁺W⁺ channel is proportional to the vacuum expectation value of the triplet (v _Φ) and, as the neutrino masses are determined from the product of the Yukawa couplings and v _Φ, then large enough v _Φ values would require unnaturally small Yukawa couplings.

Fig. 1

Feynman diagrams for pair and associated production of Φ ⁺⁺

Fig. 2

Production cross sections for pair and associated production processes at $\sqrt{s} = 7~\mbox{TeV}$

The search strategy is to look for an excess of events in one or more flavor combinations of same-sign lepton pairs coming from the decays $\varPhi^{++}\to\ell_{\alpha}^{+}\ell_{\beta}^{+}$. Final states containing three or four charged leptons are considered.

In addition to a model-independent search in each final state, where the Φ ⁺⁺ is assumed to decay in 100 % of the cases in turn in each of the possible lepton combinations (ee,μμ,ττ,eμ,eτ,μτ), the type II seesaw model is tested, following [9], at four benchmark points (BP), that probe different neutrino mass matrix structures. BP1 and BP2 describe a neutrino sector with a massless neutrino, assuming normal and inverted mass hierarchies, respectively. BP3 represents a degenerate neutrino mass spectrum with the mass taken as 0.2 eV. The fourth benchmark point BP4 represents the case in which the Φ ⁺⁺ has an equal branching fraction to each lepton generation. This corresponds to the following values of the Majorana phases: α ₁=0, α ₂=1.7. BP4 is the only case in which α ₂ is non-vanishing. For all benchmark points, vanishing CP phases and an exact tri-bimaximal neutrino mixing matrix are assumed, fixing the values of the mixing angles at $\theta_{12}=\sin^{-1}(1/\sqrt{3})$, θ ₂₃=π/4, and θ ₁₃=0. The four benchmark points, along with the model-independent search, encompass the majority of the parameter space of possible Φ ⁺⁺ leptonic decays. The values of the neutrino parameters at the benchmark points are compatible with currently measured values within uncertainties. The recent measurement of a non-zero θ ₁₃ angle [17, 18] is the only exception, and influences the branching fractions at the benchmark points by a maximum of a few percent [9]. The branching fractions at the benchmark points are summarized in Table 1.

Table 1 Branching fractions of Φ ⁺⁺ at the four benchmark points

The first limits on the Φ ⁺⁺ mass were derived based on the measurements done at PEP and PETRA experiments [19–24]. Next, the Φ ⁺⁺ was searched for at the MARK II detector at SLAC [25], the H1 detector at HERA [26] and the LEP experiments [27–30]. The latest results are from the Tevatron and ATLAS [31–33] experiments, which set lower limits on the Φ ⁺⁺ mass between 112 and 355 GeV, depending on assumptions regarding Φ ⁺⁺ branching fractions. In all previous searches, only the pair-production mechanism, and only a small fraction of the possible final state combinations, were considered. The addition of associated production and all possible final states significantly improves the sensitivity and reach of this analysis.

2 The CMS detector

The central feature of the CMS apparatus is a superconducting solenoid of 6 m internal diameter with a 3.8 T field. Within the field volume are a silicon pixel and strip tracker, a crystal electromagnetic calorimeter (ECAL) and a brass/scintillator hadron calorimeter. Muons are measured in gas-ionization detectors embedded in the steel return yoke. Extensive forward calorimetry complements the coverage provided by the barrel and endcap detectors.

CMS uses a right-handed coordinate system, with the origin at the nominal interaction point, the x axis pointing to the center of the LHC ring, the y axis pointing up (perpendicular to the LHC ring), and the z axis along the counterclockwise-beam direction. The polar angle, θ, is measured from the positive z-axis and the azimuthal angle, ϕ, is measured in the x–y plane.

The inner tracker measures charged particles within the pseudorapidity range |η|<2.5, where η=−ln[tan(θ/2)]. It consists of 1440 silicon pixel and 15 148 silicon strip detector modules, and is located in the superconducting solenoid. It provides an impact parameter resolution of ∼15 μm and a transverse momentum (p _T) resolution of about 1.5 % for 100 GeV particles. The electromagnetic calorimeter consists of 75 848 lead tungstate crystals which provide coverage in pseudorapidity |η|<1.479 in the barrel region and 1.479<|η|<3.0 in two endcap regions (EE). A preshower detector consisting of two planes of silicon sensors interleaved with a total of three radiation lengths of lead is located in front of the EE. The muons are measured in the pseudorapidity range |η|<2.4, with detection planes made using three technologies: drift tubes, cathode strip chambers, and resistive plate chambers. Matching the muons to the tracks measured in the silicon tracker results in a transverse momentum resolution between 1 and 5 %, for p _T values up to 1 TeV. The detector is highly hermetic, ensuring accurate measurement of the global energy balance in the plane transverse to the beam directions.

The first level of the CMS trigger system, composed of custom hardware processors, uses information from the calorimeters and muon detectors to select, in less than 1 μs, the most interesting events. The High Level Trigger processor farm further decreases the event rate from around 100 kHz to around 300 Hz, before data storage. A detailed description of the CMS detector may be found in Reference [34].

3 Experimental signatures

The most important experimental signature of the Φ ⁺⁺ is the presence of two like-charge leptons in the final state, with a resonant structure in their invariant mass spectrum. In this final state the background from SM processes is expected to be very small. For the four-lepton final state from Φ ⁺⁺ Φ ⁻⁻ pair production, both Higgs bosons may be reconstructed, giving two like-charge pairs of leptons with similar invariant mass.

Like-charge backgrounds arise from various SM processes, including di-boson events containing two to four leptons in the final state. The Z+jets and $\mbox{t}\overline{\mbox{t}}+\mbox{jets}$, with leptonic W decays, contribute to the non-resonant background through jet misidentification as leptons, or via genuine leptons within jets. The W+jets and QCD multijet events are examples of large cross section processes which potentially contribute to the SM background. However, the requirement of multiple isolated leptons with high transverse momentum almost entirely removes the contribution from these processes.

4 Monte Carlo simulations

The multi-purpose Monte Carlo (MC) event generator pythia 6.4.24 [35] is used for the simulation of signal and background processes, either to generate a given hard interaction at leading order (LO), or for the simulation of showering and hadronization in cases where the hard processes are generated at next-to-leading order (NLO) outside pythia, as in the case of top quark related backgrounds. The tauola [36] program is interfaced with pythia to simulate τ decay and polarization. Signal samples in the associated production mode are generated by using CALCHEP 2.5.2 [37], as pythia only contains the doubly-charged particle. The diboson and Drell–Yan events are generated using MadGraph 5.1.1.0 [38] and tauola. Samples of $\mbox{t}\overline{\mbox{t}}+\mbox{jets}$ and single-top production are generated by using powheg [39–41] and pythia.

The signal processes were simulated at 16 mass points: 130, 150, 170, 200, 225, 250, 275, 300, 325, 350, 375, 400, 450, 500, 600 and 700 GeV.

5 Event selection

5.1 Trigger

Collision events are selected through the use of double-lepton (ee, eμ, μμ) triggers. In the case of the ee and eμ triggers, a minimum p _T of 17 and 8 GeV is required of the two leptons respectively. In the case of the μμ trigger, the muon p _T thresholds changed during the data-taking period because of the increasing instantaneous luminosity. A 7 GeV p _T threshold was applied to each muon during the initial data-taking period (the first few hundred pb⁻¹). The thresholds were later raised to 13 and 8 GeV for the two muons, and then to 17 and 8 GeV. The trigger efficiency is in excess of 99.5 % for the events passing the selection defined below.

5.2 Lepton identification

The electron identification uses a cut-based approach in order to reject jets misidentified as electrons, or electrons originating from photon conversions. Electron candidates are separated into categories according to the amount of emitted bremsstrahlung energy; the latter depends on the magnetic field intensity and the large and varying amount of material in front of the electromagnetic calorimeter. A bremsstrahlung recovery procedure creates superclusters (i.e. groups of clusters), which collect the energy released both by the electron and the emitted photons. Transverse energy (E _T) dependent and η-dependent selections are applied [42].

Selection criteria for electrons include: geometrical matching between the position of the energy deposition in the ECAL and the direction of the corresponding electron track; requirements on shower shape; the impact parameter of the electron track; isolation of the electron; and further selection criteria to reject photon conversions. To reduce contamination in the signal region, electrons must pass a triple charge determination procedure based on two different track curvature fitting algorithms and on the angle between the supercluster and the pixel hits. In addition, electrons are required to have p _T>15 GeV and |η|<2.5.

Muon candidates are reconstructed using two algorithms. The first matches tracks in the silicon detector to segments in the muon chambers, whereas the second performs a combined fit using hits in both the silicon tracker and the muon systems [43]. All muon candidates are required to be successfully reconstructed by both algorithms, and to have p _T>5 GeV and |η|<2.4.

Isolation of the final state leptons plays a key role in suppressing backgrounds from $\mbox{t}\overline{\mbox{t}}$ and Z+jets. A relative isolation variable (RelIso) is used, defined as the sum of the p _T of the tracks in the tracker and the energy from the calorimeters in an isolation cone of size 0.3 around the lepton, excluding the contribution of the lepton candidate itself, divided by the lepton p _T. A typical LHC bunch-crossing at high instantaneous luminosity results in overlapping proton-proton collisions (‘pileup’). The isolation variable is corrected for energy deposition within the isolation cone by pile-up events, by means of the FastJet energy-density algorithm [44, 45]. A description of the performance of the isolation algorithm in collision data can be found in [42, 43].

In order to reconstruct hadronic τ candidates (τ _h), the ‘hadron plus strips’ (HPS) algorithm [46] is used, which is based on particle flow (PF) [47] objects. One of the main tasks in reconstructing hadronically-decaying τ is determining the number of π ⁰ mesons produced in the decay. The HPS method combines PF electromagnetic objects into ‘strips’ at constant η to take into account the broadening of calorimeter deposits due to conversions of π ⁰ decay photons. The neutral objects are then combined with charged hadrons to reconstruct the τ _h decay.

The τ _h candidates are required to have p _T>15 GeV and |η|<2.1. Additional criteria are applied to discriminate against e and μ, since these particles could be misidentified as one-prong τ _h. The τ _h candidates in the region 1.460<|η|<1.558 are vetoed, owing to the reduced ability to discriminate between electrons and hadrons in the barrel-to-endcap transition region.

In the following, the term lepton is used to indicate both light leptons (e, μ) and the τ-lepton before decay (τ). It is not possible to distinguish between leptonic τ decay products and prompt light leptons. Therefore, in scenarios that include a τ the light lepton contribution is assumed to be a mixture of prompt and non-prompt particles and selection criteria are tuned accordingly. Beyond that there is no attempt to distinguish the origin of the light leptons. As a result, a final state $\mathrm{e}^{+}\mathrm{e}^{+}\tau_{\mathrm{h}}^{-}$ could arise from $\varPhi^{++}\varPhi^{-}\rightarrow\mathrm{e}^{+}\mathrm{e}^{+}\tau^{-} \nu_{\mu}\rightarrow\mathrm{e}^{+}\mathrm{e}^{+}\tau_{\mathrm{h}}^{-} \overline{\nu}_{\tau}\nu_{\mu}$ as well as from $\varPhi ^{++}\varPhi^{-}\rightarrow\mathrm{e}^{+}\tau^{+} \tau^{-} \nu_{\mu }\rightarrow\mathrm{e}^{+}\mathrm{e}^{+}\nu_{\tau}\overline{\nu }_{\mathrm{e}}\tau_{\mathrm{h}}^{-} \overline{\nu}_{\tau}\nu_{\mu}$. In both scenarios we look for a resonance in the e⁺e⁺ invariant mass, which is narrow in the case of direct signal decay to light-leptons and wide in the case of the presence of a τ in the intermediate state. Because of the reconstruction efficiency we treat the $\mathcal{B}(\varPhi^{++}\to\tau^{+}\tau^{+})=100~\%$ assumption separately and optimize the selection criteria accordingly. However a given event may be assigned to more than one signal type if it matches the corresponding final state (the above mentioned example event would contribute to all scenarios where eτ, ττ branching fractions are non-zero assuming the event passes the respective selection criteria).

5.3 Pre-selection requirements and signal selection optimization method

In order to select events from well-measured collisions, a primary vertex pre-selection is applied, requiring the number of degrees of freedom for the vertex fit to be greater than 4, and the distance of the vertex from the center of the CMS detector to be less than 24 cm along the beam line, and less than 2 cm in the transverse plane. In case of multiple primary vertex candidates, the one with the highest value of the scalar sum of the total transverse momentum of the associated tracks is selected [48].

Data and simulated events are preselected by requiring at least two final-state light leptons, with p _T>20 GeV and p _T>10 GeV respectively. If pairs of light leptons with invariant mass less than 12 GeV are reconstructed, neither of the particles is considered in the subsequent steps of the analysis. This requirement rejects low-mass resonances and light leptons from B meson decays. In order to reduce the background contribution from QCD multijet production and misidentified leptons, the two least well-isolated light leptons are required to have summed relative isolation (∑RelIso) less than 0.35. In case of the $\mathcal{B}(\varPhi^{++}\rightarrow\tau^{+}\tau^{+})=100~\%$ assumption, the requirement is tightened to less than 0.25.

In addition, the significance of the impact parameter, SIP_ℓ=ρ _PV/Δρ _PV, is required to be less than four for the reconstructed light leptons except for the $\mathcal{B}(\varPhi^{++}\rightarrow\tau^{+}\tau ^{+})=100~\%$ assumption; here ρ _PV denotes the distance from the lepton track to the primary vertex and Δρ _PV its uncertainty.

The remaining event sample is divided into two categories, based on the total number of final state lepton candidates. The search is then performed in various final state configurations for a set of pre-determined mass hypotheses for the Φ ⁺⁺. For each mass point, the selection criteria described in Sect. 6 are optimized using simulations, by maximizing the signal significance by means of the following significance estimator:

$$S_{\mathrm{cL}} = \sqrt{2(s+b) \ln(1+s/b)-2s}, $$

where s is the signal expectation and b is the background expectation. The estimator comes from the asymptotic expression of significance $Z=\sqrt{2\log Q}$, where Q is the ratio of Poisson likelihoods P(obs|s+b) and P(obs|b). The estimator S _cL applies in the case of a counting experiment without systematic errors. We do not consider systematic errors at this stage as we select optimal cuts within the top 10 % of the significance across mass points and the small variations coming from systematic uncertainties do not change the optimization significantly. The c and L subscripts refer to counting experiment and likelihood, respectively. The size of the mass window is a part of the optimization procedure and is limited by the mass resolution of the signal.

6 Analysis categories

The analysis is separated into categories based on the total number of light leptons and τ _h in the reconstructed events.

The decay channel with $\mathcal{B}(\varPhi^{++}\rightarrow\tau \tau)=100~\%$ is handled separately, since the event topology is somewhat different from the final states with prompt decays to light leptons. In particular, the Φ ⁺⁺ reconstructed mass peak has a much larger width due to final-state neutrinos, which affects the choice and optimization of the event selection criteria.

The final signal efficiency depends on the Φ ⁺⁺ production mechanism, decay channel and chosen mass point. For pair-production process and 200 GeV Φ ⁺⁺ mass the selection efficiency varies from about 62 % in the eμ channel to 16 % in ℓτ channels and only 4 % in the ττ channel. Lower efficiency in decay channels that involve τ-leptons results from the tau ID efficiency, tighter selection criteria and the requirement of two light leptons at the trigger level. The efficiencies slightly increase at higher mass assumptions. For associated production process the selection efficiencies are decreased by about a factor of two.

6.1 ℓℓℓ and ℓℓτ _h final states

These final states are relevant for both Φ ⁺⁺ production mechanisms. The associated production process yields three charged leptons and a neutrino. The pair-production process can contribute to this category if one of the four leptons is lost due to lepton identification inefficiency or detector acceptance.

In order to separate signal from background, a set of selection criteria is optimized for significance for various combinations of final states and mass hypotheses. Three main categories of final states are considered: Φ ⁺⁺ decays to light leptons (ee, eμ and μμ), Φ ⁺⁺ decays to a light-lepton and a τ-lepton (eτ, μτ) and Φ ⁺⁺ decay to τ-leptons (ττ). Both hadronic and leptonic τ decays are considered. At least two light leptons in the final state are required because of trigger considerations.

Because of the high mass of the Φ ⁺⁺, its decay products are very energetic, allowing for signal separation through requirements on the scalar p _T sum of the three leptons (∑p _T) as a function of m _Φ. In addition, as a number of important background processes contain a Z boson, events with opposite-sign same-flavor light lepton combinations are rejected if |m(ℓ ⁺ ℓ ⁻)−m _Z| is below a channel-dependent threshold.

A selection on the opening angle between the same-charge leptons, Δφ, is also applied. Background processes, such as the production of a Z boson recoiling from a jet misidentified as a lepton, yield leptons with a larger opening angle than those originating from Z decay. For the pair-production of two signal particles we expect both lepton pairs to be boosted and the opening angle to be smaller.

A loose requirement on the missing transverse energy ($E_{\mathrm {T}}^{\text{miss}}$), defined as the negative vectorial momentum sum of all reconstructed particle candidates, is applied in the eτ,μτ and ττ channels in order to further reduce the background contributions, especially from Drell–Yan processes.

Finally, the mass window (m _lower, 1.1m _Φ) is defined. The lower bound, m _lower, depends on the final state. The mass windows are chosen by requiring high efficiency for signal events across a variety of final states (including τ leptonic decays, which contribute significantly in some scenarios), while keeping the analysis independent of the assumed relative branching fractions. The selection criteria used in this category are summarized in Table 2.

Table 2 Selections applied in the three-lepton final states

For the 100 % branching fraction scenarios, both signal and background events are filtered based on the leptonic content. For example, when showing results for 100 % branching fraction to electrons, only events containing electrons are used. For the four benchmark points, the contributions from all possible lepton combinations are taken into account and added to the relevant distributions according to the relative branching fractions. The selection criteria of eτ and μτ channel are used for the four benchmark points to account for various final state signatures.

After the application of the selection criteria, the event yields observed in data are in reasonable agreement with the sum of the expected contributions from backgrounds. The mass distributions for the simulated total background and the hypothesized BP4 benchmark point signal after applying the pre-selections are shown in Fig. 3, along with the measured yields. The event yield evolution as a function of the selections applied is also shown. For the final analysis, the background estimate is derived from data, using the methods described in Sect. 7.

Fig. 3

Left: Like-charge invariant mass distribution for the ℓℓℓ and ℓℓτ _h final state for the MC simulation and data after pre-selection. Where τ decay products are present in the final state, a visible mass is reconstructed that does not include the contribution of neutrinos. The expected distribution for a Φ ⁺⁺ with a mass of 350 GeV for the benchmark point BP4 is also shown. Right: Event yields as a function of the applied selection criteria. Δφ column includes both Δφ and $E_{\mathrm{T}}^{\text {miss}}$ selections

6.2 ℓℓℓℓ, ℓℓℓτ _h and ℓℓτ _h τ _h final states

The requirement of a fourth lepton substantially reduces the background. The Z veto is not applied for scenarios involving only light-leptons because of low signal efficiency.

A mass window around the doubly charged Higgs boson mass hypothesis is defined. It consists of a two-dimensional region in the plane of m(ℓ ⁺ ℓ ⁺) vs. m(ℓ ⁻ ℓ ⁻), where m(ℓ ⁺ ℓ ⁺) and m(ℓ ⁻ ℓ ⁻) denote the reconstructed same-sign dilepton masses. The window boundaries are the same as in Sect. 6.1. Because of the large width of the reconstructed mass peak, the mass window is not selected in the case of $\mathcal{B}(\varPhi ^{++}\rightarrow\tau^{+}\tau^{+})=100~\%$ in order to keep the signal efficiency high. The selection criteria used in this category are summarized in Table 3. The resulting mass distributions are shown in Fig. 4. Good agreement is seen between the event yields observed in the data and the expected background contributions.

Fig. 4

Left: Like-charge invariant mass distribution for the four-lepton final state for MC simulation and data after pre-selection. Where τ decay products are present in the final state, a visible mass is reconstructed that does not include the contribution of neutrinos. The expected distribution for a Φ ⁺⁺ with a mass of 350 GeV for the benchmark point BP4 is also shown. Right: Event yields as a function of the applied selection criteria

Table 3 Selections applied in various four-lepton final states

7 Background estimation from data

7.1 Sideband method

A sideband method is used to estimate the background contribution in the signal region. The sideband content is determined by using same-charge di-leptons with invariant mass in the ranges (12 GeV, m _lower) and (1.1m _Φ,500 GeV) for the three-lepton final state selection. In the case of the four-lepton final state, the sidebands comprise the Φ ⁺⁺ and Φ ⁻⁻ two-dimensional mass plane with dilepton invariant masses between 12 GeV and 500 GeV, excluding the candidate mass region. The upper bound of 500 GeV is chosen due to the negligible expected yields for both signal and background at higher masses, for the data sample used.

The sideband content is determined after the preselection requirements in order to ensure a reasonable number of events. For each Φ ⁺⁺ mass hypothesis, the ratio of the event yields in the signal region to those in the sideband, α, is estimated from the sum of all SM background MC processes:

$$\alpha=\frac{N_\text{SR}}{N_\text{SB}}, $$

where N _SR and N _SB are the event yields in the signal and sideband regions respectively, estimated from simulated event samples. Modifications to this definition are made in the case of very low event counts:

• If N _SB=0, then α=N _SR is assumed

• If N _SR is less than the statistical uncertainty, then the statistical uncertainty of the simulated samples is used as an estimate for the signal region.

With an observation of $N_{\text{SB}}^{\text{Data}}$ in a sideband, the probability density function for the expected event rate is the Gamma distribution with mean $(N_{\text{SB}}^{\text{Data}}+1)$ and dispersion $\sqrt{N_{\text{SB}}^{\text{Data}}+1}$ [49]. The predicted background contribution in the signal region is given by:

$$N_\text{BGSR} = \alpha\cdot\bigl(N_\text{SB}^{\text{Data}}+1\bigr), $$

with a relative uncertainty of $1/\sqrt{N_{\text{SB}}^{\text{Data}}+1}$, where N _BGSR is the number of background events in the signal region estimated from the data, and $N_{\text{SB}}^{\text{Data}}$ is the total number of data events in the sidebands after applying the preselection requirements. Where the background estimate in the signal region is smaller than the statistical uncertainty of the MC prediction, then it is assumed that the background estimate is equal to its statistical uncertainty.

Independently of this method, control regions for major backgrounds ($\mbox{t}\overline{\mbox{t}}$, Z+jets) are defined to verify the reliability of the simulation tools in describing the data, and good agreement is found.

7.2 ABCD method

As a mass window is not defined for the 4τ analysis, and comprises too large an area in the background region for the 3τ analysis with $m_{\varPhi^{++}}<200~\mbox{GeV}$, the sideband method cannot be used for these modes. Instead, we use the ‘ABCD method’, which estimates the number of background events after the final selection (signal region A) by extrapolating the event yields in three sidebands (B, C and D). The signal region and three sidebands are defined using a set of two observables x and y, that define four exclusive regions in the parameter space. The requirement of negligible correlation between x and y ensures that the probability density function of the background can be factorized as ρ(x,y)=f(x)g(y). It can be shown that the expectation values of the event yields in the four regions fulfill the relation λ _A/λ _B=λ _D/λ _C. The quantities λ _X are the parameters of the Poisson distribution, which for one measurement correspond to the event counts N _X. The estimated number of background events in the signal region is then given by

$$N_A = N_B\cdot\frac{N_D}{N_C}. $$

The variables ∑RelIso and |m(ℓ ⁺ ℓ ⁻)−m _Z| for the 3τ analysis and ∑RelIso and ∑p _T for the 4τ analysis are chosen based on their low correlation and the available amount of data in the sidebands. High values of RelIso populate the sidebands with background events, where jets have been misidentified as leptons. Failing the $|m(\ell^{+}\ell^{-})-m_{Z^{0}}|>50~\mbox{GeV}$ requirement gives mainly background contributions from the Drell–Yan and di-boson processes, whereas low values of ∑p _T can probe various background processes that possibly contain genuine leptons, but do not belong to the signal phase space.

The estimated number of background events agrees well with both the prediction from simulation and the number of data events observed in the signal region.

8 Systematic uncertainties

The impact on the selection efficiency of the uncertainties related to the electron and muon identification and isolation algorithms, and the relevant mis-identification rates, detailed in [42, 43, 46, 50, 51], are estimated to be less than 2 % using a standard ‘tag-and-probe’ method [52] that relies upon Z→ℓ ⁺ ℓ ⁻ decays to provide an unbiased and high-purity sample of leptons. A ‘tag’ lepton is required to satisfy stringent criteria on reconstruction, identification, and isolation, while a ‘probe’ lepton is used to measure the efficiency of a particular selection by using the Z mass constraint. The 2 % uncertainty that is assigned to lepton identification comprises also the charge misidentification uncertainty. The ratio of the overall efficiencies as measured in data and simulated events is used as a correction factor in the bins of p _T and η for the efficiency determined through simulation, and is propagated to the final result.

The τ _h reconstruction and identification efficiency via the HPS algorithm is also derived from data and simulations, using the tag-and-probe method with $\mathrm{Z}\rightarrow\tau ^{+}(\rightarrow \mu^{+}+\overline{\nu}_{\mu}+\nu_{\tau})\tau^{-}(\rightarrow\tau _{\mathrm{h}}+\nu_{\tau})$ events [46]. The uncertainty of the measured efficiency of the τ _h algorithms is 6 % [46]. Estimation of the τ _h energy-scale uncertainty is also performed with data in the Z→ττ→μ+τ _h final state, and is found to be less than 3 %. The τ _h charge misidentification rate is measured to be less than 3 %.

The theoretical uncertainty in the signal cross section, which has been calculated at NLO, is about 10–15 %, and arises because of its sensitivity to the renormalization scale and the parton distribution functions (PDF) [13].

The ratio α used to estimate the background contribution in the signal region is affected by two main uncertainties. The first is based on the uncertainty of the ratio of the simulated event yields in the sideband and the signal regions, and is related to the size of the kinematic region defined by the selection criteria. This uncertainty is dominated by the PDF and renormalization scale, in addition to the lepton energy scales. The combined uncertainty is 5 % [53]. The other component comes from the statistical uncertainty of the small event content of the sidebands. This uncertainty is as high as 100 % if no events are observed in data. The luminosity uncertainty is estimated to be 2.2 % [54].

The systematic uncertainties are summarized in Table 4. The first eight rows in the table concern the signal and the final two rows the background processes. Correlations of systematic uncertainties within a given decay mode and between different modes are taken into account in the limit calculations.

Table 4 Impact of systematic uncertainties

9 Results and statistical interpretation

The data and the estimated background contributions are found to be in reasonable agreement for all final states. Only a few events are observed with invariant masses above 200 GeV, consistent with SM background expectations. The dataset is used to derive limits on the doubly-charged Higgs mass in all decay channels. A $\mathrm{CL_{S}}$ method [55] is used to calculate an upper limit for the Φ ⁺⁺ cross section at the 95 % confidence level (CL), which includes the systematic uncertainties summarized in Table 4. As the systematic uncertainties are different for each final state, the signal and background yields are separated into five orthogonal categories, based on the number of light leptons and τ-leptons. As an example, event yields in four mass points for BP4 can be found in Table 5. A full list of mass points considered for the limit calculation is given in the end of Sect. 4. When setting limits on ‘muon and electron only’ channels, we only distinguish the cases of three and four leptons with no τ _h involved. The limits are interpolated linearly. The results of the exclusion limit calculations are reported in Figs. 5–14, and summarized in Table 6.

Fig. 5

Lower bound on Φ ⁺⁺ mass at 95 % CL for $\mathcal {B}(\varPhi^{++}\rightarrow e^{+}e^{+})=100~\%$

Fig. 6

Lower bound on Φ ⁺⁺ mass at 95 % CL for $\mathcal {B}(\varPhi^{++}\rightarrow e^{+}\mu^{+})=100~\%$

Fig. 7

Lower bound on Φ ⁺⁺ mass at 95 % CL for $\mathcal {B}(\varPhi^{++}\rightarrow\mu^{+}\mu^{+})=100~\%$

Fig. 8

Lower bound on Φ ⁺⁺ mass at 95 % CL for $\mathcal {B}(\varPhi^{++}\rightarrow e^{+}\tau^{+})=100~\%$

Fig. 9

Lower bound on Φ ⁺⁺ mass at 95 % CL for $\mathcal {B}(\varPhi^{++}\rightarrow\mu^{+}\tau^{+})=100~\%$

Fig. 10

Lower bound on Φ ⁺⁺ mass at 95 % CL for $\mathcal {B}(\varPhi^{++}\rightarrow\tau^{+}\tau^{+})=100~\%$

Fig. 11

Lower bound on Φ ⁺⁺ mass at 95 % CL for BP1. On the left hand plots the $\mathcal{B}^{2}$ means $\mathcal{B}(\varPhi ^{++}\rightarrow\ell_{\alpha}^{+}\ell_{\beta}^{+}) \mathcal{B}(\varPhi ^{++}{\rightarrow}\ell_{\gamma}^{+}\ell_{\delta}^{+})$ summed over all possible flavor combinations

Fig. 12

Lower bound on Φ ⁺⁺ mass at 95 % CL for BP2. On the left hand plots the $\mathcal{B}^{2}$ means $\mathcal{B}(\varPhi ^{++}\rightarrow\ell_{\alpha}^{+}\ell_{\beta}^{+}) \mathcal{B}(\varPhi ^{++}{\rightarrow}\ell_{\gamma}^{+}\ell_{\delta}^{+})$ summed over all possible flavor combinations

Fig. 13

Lower bound on Φ ⁺⁺ mass at 95 % CL for BP3. On the left hand plots the $\mathcal{B}^{2}$ means $\mathcal{B}(\varPhi ^{++}\rightarrow\ell_{\alpha}^{+}\ell_{\beta}^{+}) \mathcal{B}(\varPhi ^{++}{\rightarrow}\ell_{\gamma}^{+}\ell_{\delta}^{+})$ summed over all possible flavor combinations

Fig. 14

Lower bound on Φ ⁺⁺ mass at 95 % CL for BP4. On the left hand plots the $\mathcal{B}^{2}$ means $\mathcal{B}(\varPhi ^{++}\rightarrow\ell_{\alpha}^{+}\ell_{\beta}^{+}) \mathcal{B}(\varPhi ^{++}{\rightarrow}\ell_{\gamma}^{+}\ell_{\delta}^{+})$ summed over all possible flavor combinations

Table 5 Background estimation from simulation and data, observed number of events, and signal yields for BP4

Table 6 Summary of the 95 % CL exclusion limits

The cross section limits significantly improve on previously published lower bounds on the Φ ⁺⁺ mass. New limits are also set on the four benchmark points, probing a large region of the parameter space of type II seesaw models.

10 Summary

A search for the doubly-charged Higgs boson Φ ⁺⁺ has been conducted using a data sample corresponding to an integrated luminosity of 4.93±0.11 fb⁻¹collected by the CMS experiment at a center-of-mass energy of 7 TeV. No evidence for the existence of the Φ ⁺⁺ has been found. Lower bounds on the Φ ⁺⁺ mass are established between 204 and 459 GeV in the 100 % branching fraction scenarios, and between 383 and 408 GeV for four benchmark points of the type II seesaw model, providing significantly more stringent constraints than previously published limits.