Abstract
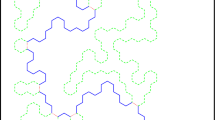
Substantial progress has been made in recent years on the 2D critical percolation scaling limit and its conformal invariance properties. In particular, chordal SLE 6(the Stochastic Loewner Evolution with parameter κ=6) was, in the work of Schramm and of Smirnov, identified as the scaling limit of the critical percolation “exploration process.” In this paper we use that and other results to construct what we argue is the fullscaling limit of the collection of allclosed contours surrounding the critical percolation clusters on the 2D triangular lattice. This random process or gas of continuum nonsimple loops in Bbb R2is constructed inductively by repeated use of chordal SLE 6. These loops do not cross but do touch each other—indeed, any two loops are connected by a finite “path” of touching loops.
Similar content being viewed by others
REFERENCES
H. Kesten, Percolation Theory for Mathematicians(Birkhäuser, Boston, 1982).
G. R. Grimmett, Percolation, second edition(Springer, Berlin, 1999).
O. Schramm, Scaling limits of loop-erased random walks and uniform spanning trees, Israel J. Math. 118:221–288 (2000).
S. Smirnov, Critical percolation in the plane:Conformal invariance, Cardy's formula, scaling limits, C. R. Acad. Sci. Paris 333:239–244 (2001).
G. Lawler, O. Schramm, and W. Werner, Values of Brownian intersection exponents I: Half-plane exponents, Acta Math. 187:237–273 (2001).
G. Lawler, O. Schramm, and W. Werner, Values of Brownian intersection exponents II: Plane exponents, Acta Math. 187:275–308 (2001).
G. Lawler, O. Schramm, and W. Werner, Values of Brownian intersection exponents III: Two-sided exponents, Ann. Inst. Henri Poincaré 38:109–123 (2002).
G. Lawler, O. Schramm, and W. Werner, Analyticity of intersection exponents for planar Brownian motion, Acta Math. 189:179–201 (2002).
G. Lawler, O. Schramm, and W. Werner, One arm exponent for critical 2D percolation, Electronic J. Probab. 7:2 (2002).
G. Lawler, O. Schramm, and W. Werner, Conformal invariance of planar loop-erased random walk and uniform spanning trees, Ann. Prob., to appear, preprint arXiv: math.PR/0112234 (2003).
G. Lawler, O. Schramm, and W. Werner, Conformal restriction:The chordal case, J. Amer. Math. Soc., arXiv:math.PR/0209343 16:417–955 (2003).
S. Smirnov and W. Werner, Critical exponents for two-dimensional percolation, Math. Rev. Lett. 8:729–744 (2001).
G. Lawler, Conformally Invariant Processes, Lecture notes for the ICTP School of Probability (2002).
W. Werner, Random Planar Curves and Schramm-Loewner Evolutions, Lecture notes from the 2002 Saint-Flour summer school (Springer, 2003), to appear, preprint arXiv: math.PR/0204277.
M. Aizenman, Scaling limit for the incipient spanning clusters, in Mathematics of Multiscale Materials; The IMA Volumes in Mathematics and its Applications, K. Golden, G. Grimmett, R. James, G. Milton, and P. Sen, eds. (Springer, 1998).
M. Aizenman and A. Burchard, Hölder regularity and dimension bounds for random curves, Duke Math. J. 99:419–453 (1999).
M. Aizenman, A. Burchard, C. M. Newman, and D. B. Wilson, Scaling limits for minimal and random spanning trees in two dimensions, Ran. Structures Alg. 15:316–367 (1999).
S. Smirnov, Critical percolation in the plane. I. Conformal invariance and Cardy's formula. II. Continuum scaling limit (long version of ref. 4, dated Nov. 15, 2001), available at http://www.math.kth.se/ ' stas/papers/index.html.
F. Camia, C. M. Newman, and V. Sidoravicius, A particular bit of universality:Scaling limits of some dependent percolation models, Comm. Math. Phys., to appear (2004).
H. Kesten, V. Sidoravicius, and Y. Zhang, Almost all words are seen in critical site percolation on the triangular lattice, Electr. J. Probab. 3(1998), 10 pp.
T. Grossman and A. Aharony, Structure and perimeters of percolation clusters, J. Phys. A 19:L745–L751 (1986).
T. Grossman and A. Aharony, Accessible external perimeter of percolation clusters, J. Phys. A 20:L1193–L1201 (1987).
M. Aizenman, B. Duplantier, and A. Aharony, Connectivity exponents and the external perimeter in 2Dindependent percolation, Phys. Rev. Lett. 83:1359–1362 (1999).
J. L. Cardy, Critical percolation in finite geometries, J. Phys. A 25:L201–L206 (1992).
J. Cardy, Lectures on Conformal Invariance and Percolation, preprint arXiv:math-ph/ 0103018 (2001).
S. Rohde and O. Schramm, Basic properties of SLE, Ann. Math., to appear, preprint arXiv:math.PR0106036 (2003).
W. Werner, Critical exponents, conformal invariance and planar Brownian motion, in Proceedings of the 3rd Europ. Congress of Math., Prog. Math., Vol. 202 (2001), pp. 87–103.
G. Lawler and W. Werner, Universality for conformally invariant intersection exponents, J. Eur. Math. Soc. 2:291–328 (2000).
L. Russo, A note on percolation, Z. Wahrsch. Ver. Geb. 43:39–48 (1978).
P. D. Seymour and D. J. A. Welsh, Percolation probabilities on the square lattice, in Advances in Graph Theory, Annals of Discrete Mathematics, Vol. 3, B. Bollobás, ed. (North-Holland, Amsterdam, 1978), pp. 227–245.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Camia, F., Newman, C.M. Continuum Nonsimple Loops and 2D Critical Percolation. Journal of Statistical Physics 116, 157–173 (2004). https://doi.org/10.1023/B:JOSS.0000037221.31328.75
Issue Date:
DOI: https://doi.org/10.1023/B:JOSS.0000037221.31328.75