Three Attractive Osculating Walkers and a Polymer Collapse Transition

Abstract

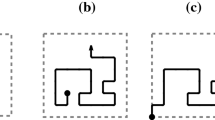
Consider n interacting lock-step walkers in one dimension which start at the points {0,2,4,...,2(n−1)} and at each tick of a clock move unit distance to the left or right with the constraint that if two walkers land on the same site their next steps must be in the opposite direction so that crossing is avoided. When two walkers visit and then leave the same site an osculation is said to take place. The space-time paths of these walkers may be taken to represent the configurations of n fully directed polymer chains of length t embedded on a directed square lattice. If a weight λ is associated with each of the i osculations the partition function is $Z_t^{(n)} (\lambda ) = \sum\nolimits_{i = 0}^{\left\lfloor {\tfrac{{(n - 1)t}}{2}} \right\rfloor } {z_{t,i}^{(n)} } \lambda ^i$ where z ⁽ⁿ⁾ _t,i is the number of t-step configurations having i osculations. When λ=0 the partition function is asymptotically equal to the number of vicious walker star configurations for which an explicit formula is known. The asymptotics of such configurations was discussed by Fisher in his Boltzmann medal lecture. Also for n=2 the partition function for arbitrary λ is easily obtained by Fisher's necklace method. For n>2 and λ≠0 the only exact result so far is that of Guttmann and Vöge who obtained the generating function $G^{(n)} (\lambda ,u) \equiv \sum\nolimits_{t = 0}^\infty {Z_t^{(n)} (\lambda )u^t }$ for λ=1 and n=3. The main result of this paper is to extend their result to arbitrary λ. By fitting computer generated data it is conjectured that Z ⁽³⁾ _t (λ) satisfies a third order inhomogeneous difference equation with constant coefficients which is used to obtain

$$G^{(n)} (\lambda ,u) = \frac{{(\lambda - 3)(\lambda + 2) - \lambda (12 - 5\lambda + \lambda ^2 )u - 2\lambda ^3 u^2 + 2(\lambda - 4)(\lambda ^2 u^2 - 1){\text{ }}c(2u)}}{{(\lambda - 2 - \lambda ^2 u)(\lambda - 1 - 4\lambda u - 4\lambda ^2 u^2 )}}$$

where $c(u) = \tfrac{{1 - \sqrt {1 - 4u} }}{{2u}}$, the generating function for Catalan numbers. The nature of the collapse transition which occurs at λ=4 is discussed and extensions to higher values of n are considered. It is argued that the position of the collapse transition is independent of n.