Abstract
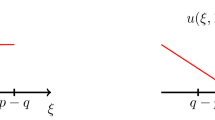
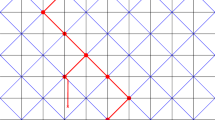
Using the Bethe ansatz, we calculate the whole large-deviation function of the displacement of particles in the asymmetric simple exclusion process (ASEP) on a ring. When the size of the ring is large, the central part of this large deviation function takes a scaling form independent of the density of particles. We suggest that this scaling function found for the ASEP is universal and should be characteristic of all the systems described by the Kardar–Parisi–Zhang equation in 1+1 dimension. Simulations done on two simple growth models are in reasonable agreement with this conjecture.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
REFERENCES
T. Halpin-Healy and Y. C. Zhang, Kinetic roughening phenomena, stochastic growth, directed polymers and all that, Phys. Rep. 254:216 (1995).
M. Kardar, G. Parisi, and Y.-C. Zhang, Dynamic scaling of growing interfaces, Phys. Rev. Lett. 56:889 (1986).
A. L. Barabási and H. E. Stanley, Fractal Concepts in Surface Growth (Cambridge University Press, 1995).
F. Family and T. Vicsek, Dynamics of Fractal Surfaces (World Scientific, Singapore, 1991).
B. Derrida and J. L. Lebowitz, Exact large deviation function in the asymmetric exclusion process, Phys. Rev. Lett. 80:209 (1998).
P. Meakin, P. Ramanlal, L. M. Sander, and R. C. Ball, Ballistic deposition on surfaces, Phys. Rev. A 34:5091 (1986).
L. H. Tang, Waiting time formulation of surface growth and mapping to directed polymers in a random medium, in Growth Patterns in Physical Sciences and Biology, E. Louis, S. M. Sander, P. Meakin, and J. M. Garcia-Ruiz, eds. (Plenum, New York, 1992).
B. Derrida and M. R. Evans, The asymmetric exclusion model: exact results through a matrix approach, in Nonequilibrium Statistical Mechanics in One Dimension, V. Privman, ed. (Cambridge University Press, 1997), p. 277.
F. R. Gantmacher, The Theory of Matrices, Vol. 2 (New York, Chelsea Pub. Co., 1959).
J. Krug, Origins of scale invariance in growth processes, Adv. Phys. 46:139 (1997).
L.-H. Gwa and H. Spohn, Six-vertex model, roughened surfaces, and an asymmetric spin Hamiltonian, Phys. Rev. Lett. 68:725 (1992).
L.-H. Gwa and H. Spohn, Bethe solution for the dynamical-scaling exponent of the noisy Burgers equation, Phys. Rev. A 46:844 (1992).
J. M. Kim and J. M. Kosterlitz, Growth in a restricted solid-on-solid model, Phys. Rev. Lett. 62:2289 (1989).
J. Kertész and D. E. Wolf, Noise reduction in Eden models: II. Surface structure and intrinsic width, J. Phys. A 21:747 (1988).
J. Krug and H. Spohn, Anomalous fluctuations in the driven and damped Sine-Gordon chain, Europhys. Lett. 8:219 (1989).
E. Ben-Naim, A. R. Bishop, I. Daruka, and P. L. Krapivsky, Mean-field theory of polynuclear surface growth, J. Phys. A. Math. Gen. 31:5001 (1998).
J. M. Kim, M. A. Moore, and A. J. Bray, Zero-temperature directed polymers in a random potential, Phys. Rev. A 44:2345 (1991).
T. Halpin-Healy, Directed polymers in random media: Probability distributions, Phys. Rev. A 44:R3415 (1991).
J. Krug, P. Meakin and T. Halpin-Healy, Amplitude universality for driven interfaces and directed polymers in random media, Phys. Rev. A 45:638 (1992).
Y. C. Zhang, Directed polymers in Hartree-Fock approximation, J. Stat. Phys. 57:1123 (1989).
C. N. Yang and C. P. Yang, Thermodynamics of a one-dimensional system of Bosons with repulsive Delta-function interaction, J. Mach. Phys. 10:1115 (1969).
D. Kim, Bethe ansatz solution for crossover scaling functions of the asymmetric XYZ chain and the Kardar-Parisi-Zhang-type growth model, Phys. Rev. E 52:3512 (1995).
D. Kim, Asymmetrix XYZ chain at the antiferromagnetic transition: Spectra and partition functions, J. Phys. A 30:3817 (1997).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Derrida, B., Appert, C. Universal Large-Deviation Function of the Kardar–Parisi–Zhang Equation in One Dimension. Journal of Statistical Physics 94, 1–30 (1999). https://doi.org/10.1023/A:1004599526997
Issue Date:
DOI: https://doi.org/10.1023/A:1004599526997