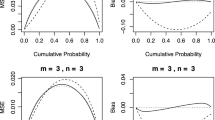
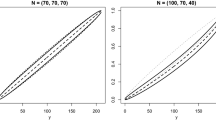
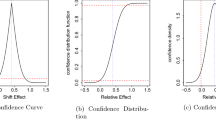
Abstract
Under a fairly general setup, we first modify the Stein-type two-stage methodology in order to incorporate some partial information in the form of a known and positive lower bound for the otherwise unknown nuisance parameter, 0(> 0). This revised methodology is then shown to enjoy various customary second-order properties and expansions for functions of the associated stopping variable, under appropriate conditions. Such general machineries are later applied in different types of estimation as well as selection and ranking problems, giving a sense of a very broad spectrum of possibilities. This constitutes natural extensions of these authors' earlier paper (Mukhopadhyay and Duggan (1997a, Sankhya Ser. A, 59, 435 448)) on the fixed-width confidence interval estimation problem exclusively for the mean of a normal distribution having an unknown variance.
Similar content being viewed by others
REFERENCES
Abramowitz, M. and Stegun, I. (1972). Handbook of Mathematical Functions, Dover, New York.
Bechhofer, R. E. (1954). A single sample multiple decision procedure for ranking means of normal populations with known variances, Ann. Math. Statist., 25, 16–39.
Bechhofer, R. E., Dunnett, C. W. and Sobel, M. (1954). A two-sample multiple decision procedure for ranking means of normal populations with a common unknown variance, Biometrika, 41, 170–176.
Chow, Y. S. and Robbins, H. (1965). On the asymptotic theory of fixed width sequential confidence intervals for the mean, Ann. Math. Statist., 36, 457–462.
Cox, D. R. (1952). Estimation by double sampling, Biometrika, 39, 217–227.
Dantzig, G. B. (1940). On the non-existence of tests of Student's hypothesis having power functions independent of δ, Ann. Math. Statist., 11, 186–192.
Desu, M. M., Narula, S. C. and Villarreal, B. (1977). A two-stage procedure for selecting the best of k exponential distributions, Comm. Statist. Theory Methods, 6, 1231–1243.
Finster, M. (1983). A frequentist approach to sequential estimation in the general linear model, J. Amer. Statist. Assoc., 78, 403–407.
Finster, M. (1985). Estimation in the general linear model when the accuracy is specified before data collection, Ann. Statist., 13, 663–675.
Ghosh, M. and Mukhopadhyay, N. (1981). Consistency and asymptotic efficiency of two-stage and sequential estimation procedures, Sankhyā Ser. A, 43, 220–227.
Ghosh, M., Mukhopadhyay, N. and Sen, P. K. (1997). Sequential Estimation, Wiley, New York.
Ghurye, S. G. (1958). Note on sufficient statistics and two-stage procedures, Ann. Math. Statist., 29, 155–166.
Mukhopadhyay, N. (1980). A consistent and asymptotically efficient two-stage procedure to construct fixed-width confidence intervals for the mean, Metrika, 27, 281–284.
Mukhopadhyay, N. (1982). Stein's two-stage procedure and exact consistency, Skandinavisk Aktuarietidskrift, 110–122.
Mukhopadhyay, N. (1988). Sequential estimation problems for negative exponential populations, Comm. Statist. Theory Methods (Reviews Section), 17, 2471–2506.
Mukhopadhyay, N. (1991). Parametric sequential point estimation, Chapter 10, Handbook of Sequential Analysis (eds. B. K. Ghosh and P. K. Sen), 245–267, Marcel Dekker, New York.
Mukhopadhyay, N. (1995). Two-stage and multi-stage estimation, Chapter 26, The Exponential Distribution: Theory, Methods and Applications (eds. N. Balakrishnan and A. P. Basu), 429–452, Gordon and Breach Publishers, Amsterdam.
Mukhopadhyay, N. (1997). Second-order properties of a two-stage fixed-size confidence region for the mean vector of a multivariate normal distribution, Statist. Tech. Report No. 97-14, University of Connecticut, Storrs.
Mukhopadhyay, N. and Abid, A. D. (1986). On fixed-size confidence regions for the regression parameters, Metron, 44, 297–306.
Mukhopadhyay, N. and Al-Mousawi, J. S. (1986). Fixed-size confidence regions for the mean vector of a multinormal distribution, Sequential Anal., 5, 139–168.
Mukhopadhyay, N. and Duggan, W. T. (1997a). Can a two-stage procedure enjoy second-order properties?, Sankhya Ser. A, 59, 435–448.
Mukhopadhyay, N. and Duggan, W. T. (1997b). On a two-stage procedure having second-order properties with applications, Statist. Tech. Report No. 97-32, University of Connecticut, Storrs.
Mukhopadhyay, N. and Solanky, T. K. S. (1994). Multistage Selection and Ranking Procedures, Marcel Dekker, New York.
Nagao, H. (1996). On fixed width confidence regions for multivariate normal mean when the covariance matrix has some structure, Sequential Anal., 15, 37–46 (Correction: ibid. (1998). 17, 125–126).
Panchapakesan, S. (1995). Selection and ranking procedures, Chapter 16, The Exponential Distribution: Theory, Methods and Applications (eds. N. Balakrishnan and A. P. Basu), 259–278, Gordon and Breach Publishers, Amsterdam.
Ray, W. D. (1957). Sequential confidence intervals for the mean of a normal population with unknown variance, J. Roy. Statist. Soc. Ser. B, 19, 133–143.
Scheffe, H. and Tukey, J. W. (1944). A formula for sample sizes for population tolerance limits, Ann. Math. Statist., 15, p. 217.
Stein, C. (1945). A two sample test for a linear hypothesis whose power is independent of the variance, Ann. Math. Statist., 16, 243–258.
Stein, C. (1949). Some problems in sequential estimation (abstract), Econometrica, 17, 77–78.
Wang, Y. H. (1980). Sequential estimation of the mean of a multinormal population, J. Amer. Statist. Assoc., 75, 977–983.
Woodroofe, M. (1977). Second order approximations for sequential point and interval estimation, Ann. Statist., 5, 984–995.
Author information
Authors and Affiliations
About this article
Cite this article
Mukhopadhyay, N., Duggan, W. On a Two-Stage Procedure Having Second-Order Properties with Applications. Annals of the Institute of Statistical Mathematics 51, 621–636 (1999). https://doi.org/10.1023/A:1004074912105
Issue Date:
DOI: https://doi.org/10.1023/A:1004074912105