1 Introduction

With increased customer demands and tough vehicle safety regulations, increasing attentions have recently been drawn to achieving better crashworthiness of automobile [1,2,3]. Moreover, environmental sustainable developments and energy crisis have forced engineers to design increasingly lighter structures [4,5,6]. Structures that possess with characteristics and superior crashworthiness have drawn abundant attention for their better performance [7, 8]. Owing to outstanding capabilities of energy absorption, thin-walled structure is regarded as the most potential energy absorber.

To enhance energy absorption performance, substantial efforts on design shape optimization have been expended. Rossi [9] carried out the study on the crushing behavior among square, hexagonal and octagonal tubes. Gao et al. [10] carried out simulations on crushing impact of thin-walled tubes with various cross-sections, which provided reference for the selection of automotive cross-section. Thin-walled tubes should be equipped with energy absorption performance and possessed with stiffness requirements. For example, outer thin wall of front side rail should be equipped with high stiffness. It is, however, not always wise to enhance crashworthiness by sacrificing stiffness when using the aforementioned optimization methods. Therefore, this paper proposes the concept of decoupling to satisfy the contradictory requirements of structural stiffness and energy absorption, i.e., the outer thin wall needs high stiffness, while the thinner filler is responsible for strengthening energy absorption. Substantial research on thin-walled tubes with fillers has been conducted. Axial crushing analysis on foam-filled thin-walled structure was carried out by Ghamarian [11] and Zarei [12]. Ahmad et al. [13] emulate crushing behaviors of foam-filled conical tubes adopting numerical methods. Whereas, the above-mentioned studies only involve single performance and conventional positive Poisson’s ratio foam fillers. Positive Poisson’s ratio fillers usually possess unstable platform stress and higher peak stress which limit the improvement in energy absorption and further application of impact protection. Various re-entrant structures have also been studied. Ma et al. [14] proposed a type of re-entrant square cellular structure and illustrated the effects of cellular structural parameters on in-plane dynamic performance. Compressing this kind of structure results in structural contraction, and platform stress improves, which contributes greatly to enhancing the capability for energy absorption. Herein, re-entrant triangles honeycomb acts as a filler, and the octagonal and cruciform cross-section is regarded as the stiffener.

To satisfy the requirements of structural stiffness and energy absorption simultaneously, the novel tube utilizes re-entrant triangles as filler based on the concept of decoupling structural stiffness and energy absorption. Inner re-entrant triangles are utilized to meet the demands of energy absorption, while the octagonal and cruciform cross-section is designed to achieve higher stiffness.

Firstly, relationships among geometric parameters and relative density, equivalent elastic modulus and energy absorption characteristics are established, which are validated by experiments. The optimal geometric parameters of unit cell are then sought to maximize unit volume energy absorption and minimize relative density utilizing the NSGA-II method. Subsequently, the cross-section of tube with optimal stiffness is obtained by employing static topology optimization method with targets for maximizing axial stiffness and lateral stiffness. To certify the optimization method, RTT, PFT, NTT and PST are analyzed and compared in light of stiffness and energy absorption. The proposed RTT demonstrates superior energy absorption and structural stiffness, and this work proposes a design method of decoupling structural stiffness and energy absorption and applying re-entrant triangles on tube inside. The novel RTT presents prominent effects on energy absorption and structural stiffness. The results are encouraging in the sense that it offers another potential material for engineers to address the issue and the novel-type RTT with re-entrant triangles can be widely promoted and achieve further applications on new energy absorbent structures.

2 Theoretical Models of Re-entrant Triangles Honeycomb

In order to set up the relationship among structural parameters and relative density, equivalent elastic modulus and energy absorption, theoretical models of the honeycomb are established. On the hypothesis that cellular material is continuous, parameters can be utilized to represent performance of cellular structure. The equivalent description is called as asymptotic homogenization method, put forward by Benssousan [15] and Sanchez-Palentia [16]. Asymptotic homogenization methods [17,18,19] have been regarded as effective means for multiscale modeling, while these methods are always neglected in the aspect of mechanics during the homogenization process and widely used in the prediction of equivalent performance of composites. Asymptotic homogenization method focuses on the theory where main concepts and derivation of the equations for computation of effective constitutive parameters of complex materials with the unit cell. It acts as a bridge-linking microscale analysis and macroscopic properties of cellular structures; structural response is obtained from the perspective of macroscopic scale. If size of macroscopic structure is larger compared with microscopic unit cell and the number of unit cell is sufficient, more accurate results can be expected by utilizing homogenization method.

2.1 Relationship Between Relative Density and Geometric Parameters

Based on the homogenization method, Fig. 1 exhibits periodic re-entrant triangles and representative unit cell.

Fig. 1
figure 1

Periodic re-entrant triangles and representative unit cell

Full size image

To date, much pioneering work has been conducted to set up the connections among cell geometry and mechanical properties of cellular structure. Relative density is considered as a critical parameter to illustrate its features [20]. For two-dimensional (2D) unit cell, relative density \(\rho_{{ 2 {\text{D}}}}\) is described in Eq. (1) and Fig. 2.

Fig. 2
figure 2

Relative density of 2D unit cell

Full size image
$$\rho_{{ 2 {\text{D}}}} = \frac{{S_{1} }}{{S_{2} }}$$
(1)

It can be seen that \(\rho_{{ 2 {\text{D}}}}\) is dominated by \(S_{1}\) and \(S_{2}\), which represent the areas of internal cell wall and 2D unit cell, respectively.

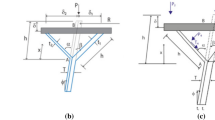
Figure 3 exhibits geometric variables. Where \(L\), \(M\) and \(N\) stand for the lengths of long cell beam, short cell beam and horizontal beam accordingly,\(H\) indicates distance between two horizontal beams, \(\varphi\) stands for the intersection angle between long cell beam and \(Y\)-axis, while \(\theta\) is the angle of short cell wall and \(Y\)-axis, \(T_{L}\) and \(T_{M}\) represent cellular thicknesses of long beam and short beam, respectively. Most importantly, \(\theta\) must be greater than \(\varphi\) in light of re-entrant characteristics. Meanwhile, thickness coefficient \(\alpha\) and length coefficient \(\beta\) are introduced, \(\alpha = \frac{{T_{L} }}{L}\), \(\alpha = \frac{{T_{M} }}{M}\), \(\beta = \frac{N}{L}\). To simplify the expression \(\rho_{2D}\), parameter \(K = \frac{M}{L}\), scaling factor of length, is introduced.

Fig. 3
figure 3

Geometric description of 2D unit cell

Full size image

Using the latter facts and substituting the series into Eq. (1), relative density \(\rho_{{ 2 {\text{D}}}}\) is finally obtained.

$$\rho_{2D} = \frac{{\alpha + \alpha \beta + \alpha K^{2} + \alpha \beta K}}{{\left( {\cos \varphi - \sqrt {K^{2} - \sin^{2} \varphi } + \alpha + \alpha K} \right)\left( {\sin \varphi + \beta } \right)}}$$
(2)

Similarly, the relative density of two-dimensional (3D) cells is given by

$$\rho_{\text{3D}} = \frac{{V_{1} }}{{V_{2} }}$$
(3)

where \(V_{1}\) stands for the volume of cellular structure, \(V_{2}\) is volume of unit cell, \(b\) manifests cell thickness along \(Z\) direction, giving

$$V_{1} = S_{1} b - \left( {\frac{b}{2}} \right)^{2} \left( {T_{L} + T_{M} } \right)$$
(4)
$$V_{2} = S_{2} \left( {\frac{1}{2}N + \frac{1}{2}N + L\sin \varphi } \right) = S_{2} \left( {\beta L + L\sin \varphi } \right)$$
(5)

Similar to \(\rho_{2D}\) and width coefficient \(\gamma\), \(\gamma = \frac{b}{L}\), relative density \(\rho_{\text{3D}}\) yields

$$\rho_{\text{3D}} = \frac{{\gamma S_{1} - \frac{{b^{2} \alpha }}{2}}}{{\left( {\sin \varphi + \beta } \right)S_{2} }} \approx \frac{\gamma }{\sin \varphi + \beta }\rho_{2D}$$
(6)

2.2 Mathematical Descriptions of Equivalent Elastic Modulus and Plateau Stress

Linear elastic response of this re-entrant triangle is primarily caused by the bending cell walls. Axial extension or compression and shear deformation of the cell beams can be ignored, and strains are small enough to avoid the gross changes in geometry. To simplify the analysis, following hypothesis is set that cellular angle \(15{^\circ } \le \varphi \le 40{^\circ }\), thickness coefficient \(0.05 \le \alpha \le 0.25\), length coefficient \(\beta\) is set from 0.1 to 0.3; the short cell beam should be possessed with re-entrant characteristics, i.e., \(\sin \varphi < K < 1\). To reduce the complexity of optimal design, the width coefficient \(\gamma\) and thickness coefficient \(\alpha\) are kept the same: \(\gamma = \alpha\). The mechanical model can be exhibited in the following Fig. 4.

Fig. 4
figure 4

Axial compression mechanical model

Full size image

According to standard rail theory [21], long cell beam \(l_{L}\) deflects by

$$\delta_{L} = \frac{{P\sin \varphi L^{3} }}{{3EI_{L} }} - \frac{{TL^{2} }}{{2EI_{L} }}$$
(7)

where \(T\) stands for the applied moment tending to bend the wall, \(I_{L}\) represents the second moment of inertia of the long beam \(l_{L}\),\(E\) denotes the elastic modulus of the material used and \(P\) is given by

$$P = \sigma b\left( {\frac{1}{2}N + \frac{1}{2}N + L\sin \varphi } \right) = \sigma b\left( {\beta L + L\sin \varphi } \right)$$
(8)

Of which, \(\sigma\) is the applied stress along the \(Y\) direction. Hence, the deflection of long cell beam \(l_{L}\) yields

$$\delta_{L} = \frac{{P\sin \varphi L^{3} }}{{3EI_{L} }} - \frac{{TL^{2} }}{{2EI_{L} }} = \frac{{\sigma L\left( {\beta + \sin \varphi } \right)\sin \varphi }}{{E\alpha^{3} }}$$
(9)

Similarly, the deflection of short cell beam \(l_{S}\) is given by

$$\delta_{M} = \frac{{P\sin \theta M^{3} }}{{3EI_{M} }} - \frac{{TM^{2} }}{{2EI_{M} }} = \frac{{\sigma L\left( {\beta + \sin \varphi } \right)\sin \theta }}{{E\alpha^{3} }}$$
(10)

Strain \(\varepsilon_{x}\) and \(\varepsilon_{y}\) along \(X\) and \(Y\) axes, respectively, are then given by

$$\varepsilon_{x} = \frac{{\delta_{M} \cos \theta - \delta_{L} \cos \varphi }}{\beta L + L\sin \varphi }$$
(11)
$$\varepsilon_{y} = \frac{{\delta_{L} \sin \varphi + \delta_{M} \sin \theta }}{H}$$
(12)

Combined with the above-mentioned equations, the equivalent elastic modulus \(E_{\text{eq}}\) and equivalent Poisson’s ratio \(\nu_{\text{eq}}\) are given by

$$E_{\text{eq}} = \frac{\sigma }{{\varepsilon_{y} }} = \frac{{E\alpha^{3} \left( {\cos \varphi - \sqrt {K^{2} - \sin^{2} \varphi } } \right)}}{{\left( {\beta + \sin \varphi } \right)\left( {1 + \frac{1}{{K^{2} }}} \right)\sin^{2} \varphi }}$$
(13)

Similar to 2D cells, applied stress \(\sigma_{\text{3D}}\) of 3D cells is then

$$\sigma_{\text{3D}} = \frac{\gamma }{\beta + \sin \varphi }\sigma$$
(14)

Thus, the equivalent elastic modulus \(E_{\text{3D}}\) of 3D cells is described as

$$E_{\text{3D}} = \frac{\gamma }{\beta + \sin \varphi }E_{\text{eq}}$$
(15)

Average stress of plateau region is regarded as plateau stress in stress–strain curve [22]. Plateau stress acts as a key factor to improve capabilities of energy absorption effectively, that is, energy absorption attributes significantly to plateau stress. Plateau stress also has a close relationship with the structural failure mechanism. Hence, it is of significance to further study the predominant deformation mode of these re-entrant triangles. Because the cellular structure is subjected to axial compression, the structural deformation is uniform in the elastic stage. As loading stress exceeds the stress limit, a series of failure modes including elastic buckling, plastic collapse and brittle fracture will occur.

According to the pioneering work [23], plastic collapse and elastic buckling are the two main failure modes for cellular structure comprising elastic–plastic materials. Elastic buckling comes up when the loading is greater than Euler buckling load \(F_{\text{cr}}\) [24]. When component force \(P_{L}\) along the long cell beam is equal to \(F_{cr}\), elastic bulking occurs. Plastic collapse comes up as bending moment reaches or beyond the fully plastic moment. Under these conditions, the work of the long and short cell beams \(W_{L}\) and \(W_{M}\) are, respectively, expressed as

$$W_{L} = \frac{1}{2}\gamma \cdot \sigma \left( {\beta + \sin \varphi } \right)L^{2} b\sin \varphi$$
(16)
$$W_{M} = \frac{1}{2}\gamma \cdot \sigma b\left( {\beta L + M\sin \theta } \right)M\sin \theta$$
(17)

where \(\gamma\) implies the angle through which all joints of the cell wall rotate. Besides, the work done by the plastic hinges can be described as

$$W_{P} = \frac{1}{2}\sigma_{\text{ys}} bT^{2} \gamma$$
(18)
$$W_{PL} = \frac{1}{2}\sigma_{\text{ys}} bT_{L}^{2} \gamma$$
(19)
$$W_{PM} = \frac{1}{2}\sigma_{\text{ys}} bT_{M}^{2} \gamma$$
(20)

The critical stresses \(\sigma_{L}\) and \(\sigma_{M}\) of long beam and short beam are given by the following equations. Among this, \(\sigma_{\text{ys}}\) means yield stress.

$$\sigma_{L} = \frac{{\sigma_{\text{ys}} \alpha^{2} }}{{\left( {\beta + \sin \varphi } \right)\sin \varphi }}$$
(21)
$$\sigma_{M} = \frac{{\sigma_{\text{ys}} \alpha^{2} \sin \varphi }}{{\left( {\beta + \sin \varphi } \right)\sin^{2} \theta }}$$
(22)

In view of structural characteristics, \(\sin \varphi < \sin \theta\). Hence, \(\frac{{\sigma_{L} }}{{\sigma_{M} }} = \frac{{\sin^{2} \theta }}{{\sin^{2} \varphi }} > 1\), \(\sigma_{L} > \sigma_{M}\). Therefore, the critical stress \(\sigma_{M}\) of short cell wall contributes greatly to the cellular stress limit, giving

$$\sigma_{\text{pl}} = \sigma_{M} = \frac{{K^{2} \alpha^{2} \sigma_{\text{ys}} }}{{\left( {\beta + \sin \varphi } \right)\sin \varphi }}$$
(23)

The elastic bulking \(\sigma_{eb}\) exceeds the plastic collapse \(\sigma_{\text{pl}}\), giving

$$\frac{{\sigma_{\text{ys}} }}{E} < \frac{{n^{2} \pi^{2} \alpha \sin^{2} \theta }}{6\sin 2\varphi }$$
(24)

For metals and polymers belonging to conventional elastic materials, order of magnitude of \(\frac{{\sigma_{\text{ys}} }}{E}\) is \(10^{ - 3}\) and \(10^{ - 2}\). Through calculation, plastic collapse proves to be the dominant failure mode. Similar analysis on equivalent plastic collapse stress can be conducted for 3D cells. As the concentrated force resulting in complete plastic hinges of 3D cells is equal to that of 2D cell, applied stress on 3D re-entrant cells is acquired

$$\sigma_{\text{pl,3D}} = \frac{{K^{2} \alpha^{2} \sigma_{\text{ys}} }}{{\left( {\beta + \sin \varphi } \right)\sin \varphi }} \cdot \frac{\alpha }{\beta + \sin \varphi } = \frac{{K^{2} \alpha^{3} \sigma_{\text{ys}} }}{{\left( {\beta + \sin \varphi } \right)^{2} \sin \varphi }}$$
(25)

2.3 Characterization of Energy Absorption Under Quasi-Static Compression

As cellular structures with re-entrant features are subjected to external force, energy absorption can be illustrated by the work of external force, i.e., the area surrounding the collision force–displacement curve and the displacement axis. The collision force–displacement curve is associated with the overall size of structure, so it can be transformed into a stress–strain curve in order to show different energy absorption characteristics for structures of various sizes. Unit volume energy absorption \(W\) is denoted by the area under stress–strain curve and horizontal axis, given by

$$W = \int_{0}^{{\varepsilon_{D} }} {\sigma \left( \varepsilon \right)} {\text{d}}\varepsilon$$
(26)

where \(\varepsilon_{D}\) and \(\sigma \left( \varepsilon \right)\) are the densification strain and instantaneous stress, respectively.

The stress–strain curve can be utilized to analyze energy absorption characteristics and evaluate cell shape of the re-entrant cellular structure. Effective unit volume energy absorption \(W\) comprises three parts: the elastic region \(W_{1}\), plateau region \(W_{2}\) and plateau stress enhancement region \(W_{3}\).

In the elastic region, the following assumption is set that the relationship between stress and strain is linear. Unit volume energy absorption in the elastic region is written as

$$W_{1} = \frac{{\sigma^{2} }}{{2E_{\text{3D}} }} = \frac{{\sigma_{\text{pl,3D}}^{2} \sin^{2} \varphi \left( {\beta + \sin \varphi } \right)^{2} \left( {1 + \frac{1}{{K^{2} }}} \right)}}{{2E\alpha^{4} \left( {\cos \varphi - \sqrt {K^{2} - \sin^{2} \varphi } } \right)}}$$
(27)

Total energy absorption in the plateau region comprises energy absorbed under constant plateau stress and energy absorbed in plateau stress enhancement region. Under constant plateau stress, energy absorption can be written as

$$W_{2} = \sigma_{\text{pl,3D}} \left( {\varepsilon_{E} - \varepsilon_{0} } \right)$$
(28)

where \(\varepsilon_{0}\) depicts the strain at the end of the elastic region, \(\varepsilon_{0} = \frac{{\sigma_{\text{pl,3D}} }}{{E_{\text{3D}} }}\). \(\varepsilon_{E}\) is plateau stress enhancement strain, \(\varepsilon_{E} = A\varepsilon_{D}\); coefficient \(A\) can be obtained by simulation analysis.

The following empirical formula exhibits densification strain \(\varepsilon_{D}\) [21]. Where,\(B\), \(C\) and \(D\) are the coefficients, which can be determined by the simulation approach.

$$\varepsilon_{D} = B\left( {1 - C\rho_{\text{3D}} + D\rho_{\text{3D}}^{3} } \right)$$
(29)

The volume of the cellular structure as it reaches the plateau stress enhancement region is given by

$$V_{E} = L^{2} H\left( {\varepsilon_{D} - \varepsilon_{E} } \right)$$
(30)

The instantaneous volume of the cellular structure can be expressed as

$$V\left( \varepsilon \right) = V_{E} - \left( {L + \nu \varepsilon_{0} L} \right)^{2} \left( {\varepsilon H - \varepsilon_{E} H} \right)$$
(31)

where \(\varepsilon_{E} < \varepsilon < \varepsilon_{D}\).

In plateau stress enhancement region, instantaneous relative density can be given by

$$\frac{\rho (\varepsilon )}{{\rho_{E} }} = \frac{{\varepsilon_{D} \left( {1 - A} \right)}}{{\varepsilon_{D} \left( {1 - A} \right) - \left( {1 + \varepsilon_{0} \nu_{\text{3D}} } \right)^{2} \left( {\varepsilon - A\varepsilon_{D} } \right)}}$$
(32)

For 3D cellular structure composed of elastic–plastic materials, relative density is proportional to the square of \(\alpha\), and equivalent plastic collapse stress is proportional to vertical component of \(\alpha\). Thus, the instantaneous stress in plateau stress enhancement region is expressed as:

$$\sigma \left( \varepsilon \right) = \sqrt {\left( {\frac{{\varepsilon_{D} \left( {1 - A} \right)}}{{\varepsilon_{D} \left( {1 - A} \right) - \left( {1 + \varepsilon_{0} \nu_{\text{3D}} } \right)^{2} \left( {\varepsilon - A\varepsilon_{D} } \right)}}} \right)^{3} } \sigma_{\text{pl,3D}}$$
(33)
$$W_{3} = \int_{{A\varepsilon_{D} }}^{{\varepsilon_{D} }} {\sqrt {\left( {\frac{{\varepsilon_{D} \left( {1 - A} \right)}}{{\varepsilon_{D} \left( {1 - A} \right) - \left( {1 + \varepsilon_{0} \nu_{\text{3D}} } \right)^{2} \left( {\varepsilon - A\varepsilon_{D} } \right)}}} \right)^{3} } } \frac{{K^{2} \sigma_{\text{ys}} \alpha^{3} }}{{\left( {\beta + \sin \varphi } \right)^{2} \sin \varphi }}d\varepsilon$$
(34)

3 Certification of Theoretical Models

With the purpose of verifying the theoretical models obtained above, three groups of parameters are listed in Table 1.

Table 1 Three groups of geometric parameters
Full size table

Based on the selected three groups of parameters, theoretical results are obtained. Besides, the quasi-static compression mechanical testing on re-entrant triangles is performed. The re-entrant triangles structure is made of aluminum alloy with density \(\rho = 2.7e^{ - 6} \,{\text{Kg/mm}}^{3}\), Young’s modulus \(E = 68.21\,{\text{Gpa}}\), Poisson’s ratio \(\nu = 0.3\), yield strength \(\sigma_{\text{ys}} = 80\,{\text{Mpa}}\) and ultimate strength \(\sigma_{\text{us}} = 173\,{\text{Mpa}}\). The cellular structure is constrained at top and bottom by steel plates. The axial loading is applied on the top of the cellular structure with the velocity of 1 mm/min. Figure 5 presents the pre-compression and post-compression of the specimen under quasi-static loading. Then, the experimental and theoretical stress–strain curves are achieved and compared.

Fig. 5
figure 5

Pre-compression and post-compression of the specimen under quasi-static loading

Full size image

Figure 6 shows that the experiment results of the re-entrant triangles honeycomb are fluctuating up and down; this is due to the plastic collapse deformation mode of the structure layer by layer. It also shows that the results of experimental analysis match well with theoretical results and varying tendencies of the curves tend to be consistent. There exist relations between unit volume energy absorption \(W_{u}\) and stress–strain curve, and \(W_{u}\) can be described by the surrounded area between stress–strain curve and \(X\)-axis. Hence, Table 2 can be obtained, and it proves that theoretical results of \(W_{u}\) maintain a high agreement with that of experimental results. Theoretical models derived above prove to be reasonable and appropriate by means of test.

Fig. 6
figure 6

Comparisons of theoretical and experimental stress–strain curves

Full size image
Table 2 Comparisons of theoretical and experimental results for unit volume energy absorption
Full size table

4 Optimization of Unit Cell

4.1 Single Objective Optimization on Maximizing Unit Volume Energy Absorption

With the purpose of achieving the optimal geometric parameter, multi-objective optimization on unit cell is executed. The NSGA-II method is adopted with the objectives for maximum \(W_{u}\) and minimum \(\rho_{RD}\).

While re-entrant triangles act as an energy absorption equipment, maximization of unit volume energy absorption occupies a leading position. \(W_{u}\) is closely related to thickness coefficient \(\alpha\), length coefficient \(\beta\), cellular angle \(\varphi\) and scaling factor of length \(K\). The corresponding optimization model is given by

$$\begin{aligned} {Objective:} \hbox{max} W_{u} (\alpha ,\beta ,\varphi ,K) \hfill \\ s.t.\left\{ {\begin{array}{*{20}c} {0 < \alpha < 1} \\ {0 < \varphi < 90^{ \circ } } \\ {\sin \varphi < K < 1} \\ {\frac{{\alpha \left( {1 + K} \right)}}{\cos \varphi } + \frac{\beta }{2} < \sin \varphi } \\ \end{array} } \right\} \hfill \\ \end{aligned}$$
(35)

The optimization process is shown in Fig. 7, where the optimal \(W_{u}\) is obtained after 400 iterations.

Fig. 7
figure 7

Optimization process of unit volume energy absorption \(W_{u}\) for unit cell

Full size image

4.2 Single Objective Optimization on Minimizing Relative Density

Lightweight plays an essential role in automotive design process. The corresponding optimization model of minimizing relative density can be expressed as follows.

$$\begin{aligned} {Objective:} \hbox{min} \rho_{RD} (\alpha ,\beta ,\varphi ,K) \hfill \\ s.t.\left\{ {\begin{array}{*{20}c} {0 < \alpha < 1} \\ {0 < \varphi < 90^{ \circ } } \\ {\sin \varphi < K < 1} \\ {\frac{{\alpha \left( {1 + K} \right)}}{\cos \varphi } + \frac{\beta }{2} < \sin \varphi } \\ \end{array} } \right\} \hfill \\ \end{aligned}$$
(36)

Similarly, Fig. 8 exhibits the specific optimization process of relative density for unit cell. It shows that the optimal \(\rho_{RD}\) can be achieved through 350 iterations.

Fig. 8
figure 8

Optimization process of relative density \(\rho_{RD}\) for unit cell

Full size image

4.3 Multi-objective Optimization of Unit Cell

Generally, several objectives should be taken into account in structural design simultaneously. Hence, it is indispensable to search a balance among various objectives. The multi-objective optimization model can be constructed as

$$\begin{aligned} {Objective:}\left\{ {\begin{array}{*{20}c} {\hbox{max} W_{u} (\alpha ,\beta ,\varphi ,K)} \\ {\hbox{min} \rho_{RD} (\alpha ,\beta ,\varphi ,K)} \\ \end{array} } \right. \hfill \\ s.t.\left\{ {\begin{array}{*{20}c} {0 < \alpha < 1} \\ {0 < \varphi < 90^{ \circ } } \\ {\sin \varphi < K < 1} \\ {\frac{{\alpha \left( {1 + K} \right)}}{\cos \varphi } + \frac{\beta }{2} < \sin \varphi } \\ \end{array} } \right\} \hfill \\ \end{aligned}$$
(37)

where \(W_{u}\) represents unit volume energy absorption, \(\rho_{RD}\) denotes relative density of re-entrant triangles structure, \(K\) stands for scaling factor of length, \(\varphi\) is cellular angle and\(\alpha\) and \(\beta\) are thickness coefficient and length coefficient, respectively.

Multiple Pareto non-inferior solutions can be acquired through multi-objective genetic algorithm optimization. An evaluation function \(Q\) is proposed herein to search for the optimal result. Based on the definition of evaluation function, the solution improves as the satisfaction decreases:

$$Q = \omega_{1} \frac{{\left( {\rho (\alpha ,\beta ,K,\varphi ) - \rho_{\hbox{min} } } \right)}}{{(\rho_{\hbox{max} } - \rho_{\hbox{min} } )}} + \omega_{2} \frac{{(W_{\hbox{max} } - W_{u} (\alpha ,\beta ,K,\varphi ))}}{{(W_{\hbox{max} } - W_{\hbox{min} } )}}$$
(38)

where \(\rho_{{\text{max}}}\) and \(\rho_{{\text{min}}}\) represent the maximum and minimum of relative density in optimal solutions, respectively. \(W_{{\text{max}}}\) and \(W_{{\text{min}}}\) stand for maximum and minimum unit volume energy absorption in optimal solutions and\(\omega_{1}\) and \(\omega_{2}\) denote the weighting coefficients of relative density and unit volume energy absorption. The multi-optimization process is explained in Fig. 9. The optimal evaluation function \(Q\) is obtained through 400 iterations. Weighting coefficients are \(\omega_{1} = 0.4\) and \(\omega_{2} = 0.6\), respectively. Through the optimization process, the optimal structural parameters of unit cell are displayed in Table 3.

Fig. 9
figure 9

Multi-optimization of unit volume energy absorption \(W_{u}\) and relative density \(\rho_{RD}\) for unit cell

Full size image
Table 3 The optimal geometric parameters
Full size table

5 Topology Optimization of Thin-Walled Tube

Based on above analysis, the re-entrant triangles honeycombs with the optimal parameters will be embedded into thin-walled tube to improve energy absoprtion performance, whereas the cross-section of tube should be determined firstly. An automotive front side rail is a critical component of load bearing and safety protection. This paper takes front side rail as an example. Based on the decoupling thought, filler re-entrant triangles honeycomb is utilized to satisfy energy absorption performance, and outer thin wall should meet high structural stiffness. In order to obtain the cross-section shape profile, static topology optimization is conducted with targets for maximizing axial stiffness and lateral stiffness. On the basis of static topology optimization, dynamic topology optimization of impact energy absorption of thin-walled tube is also conducted to compare the RTT with the NTT design.

5.1 Theories of Static Topology Optimization

Variable density method is the most commonly utilized method of continuous topology optimization [25, 26]. On the hypothesis that the material in structure is changeable, as the topology optimization model is established, the elements with the density less than the threshold value governed by certain rules are omitted [27]. Then topological structure is realized and optimal allocation of structural materials can be achieved. With the target for maximum stiffness, the relative density of material \(x_{i}\) (\(i = 1,2, \ldots ,n\)) is set as a variable of topological design. The optimization objective is structural minimum compliance. In view of equilibrium conditions and mass constraints, mathematical models of topology optimization are given by

$$\begin{aligned} findx_{i} ,(i = 1,2, \ldots ,n); \hfill \\ objective:\hbox{min} C = F^{\text{T}} S = S^{\text{T}} KS \hfill \\ s.t.:\left\{ {\begin{array}{*{20}l} {\sum\limits_{i = 1}^{N} {{\raise0.7ex\hbox{${m_{i} }$} \!\mathord{\left/ {\vphantom {{m_{i} } M}}\right.\kern-0pt} \!\lower0.7ex\hbox{$M$}}} \le M^{\text{f}} } \\ {0 < x_{\hbox{min} } \le x_{i} \le x_{\hbox{max} } \le 1} \\ {F = KS} \\ \end{array} } \right. \hfill \\ \end{aligned}$$
(39)

Here, \(C\) is compliance,\(F\) stands for applied load, \(S\) represents structural displacement, \(K\) expresses structural stiffness, \(x_{\hbox{min} }\) denotes lower bound of relative density, \(x_{\hbox{max} }\) is upper bound of relative density, \(m_{i}\) indicates the mass of unit \(i\) and \(M\) and \(M^{\text{f}}\) are initial total mass and target mass fraction. Among this, for the thin-walled tube with re-entrant triangles structure, \(M^{\text{f}} = \frac{{M^{'} - M_{ACM} }}{M}\) and for the one without re-entrant triangles structure, \(M^{\text{f}} = \frac{{M^{'} }}{M}\). \(M^{'}\) represents the mass of PST, and \(M_{ACM}\) is the total mass of re-entrant triangles structure fully filled with solids.

Static topology optimization method is composed of several steps; the first step is to define design space of topology optimization. Then finite element model is constructed; load and boundary conditions are also established. Optimization parameters are subsequently set up. Finally, the calculation is implemented in HyperWorks software. Based on convergence situations, if the results cannot meet the convergence criterion, recalculation should be executed by modifying the design variables. Otherwise, the optimal results are obtained. A flow diagram of static topology optimization is described in Fig. 10.

Fig. 10
figure 10

Flow diagram of static topology optimization

Full size image

5.2 Static Topology Optimization

Based on the profile of a car model’s front side rail, a rectangular structure of \(100\,{\text{mm}} \times 100\,{\text{mm}} \times 300\,{\text{mm}}\) is adopted as initial design space for optimization. The front side rail is meshed with hexahedral elements, and the bottom is clamped with all the degrees of freedom restricted. Figure 11 exhibits boundary conditions of the traditional one. Uniform distributed pressure is applied to both axial and side loadings. Element density is set as design variable, minimum strain energy is regarded as objective function, and mass fraction is considered as constraint. Meanwhile, extrusion molding process constraints are also considered.

Fig. 11
figure 11

Boundary conditions for static topology optimization

Full size image

The static topology optimization is conducted using the OptiStruct solver of HyperWorks software; final optimization results are displayed in Fig. 12.

Fig. 12
figure 12

Optimal results of static topology optimization

Full size image

The topological optimization results are subsequently pruned according to the requirements of the actual manufacturing process. The optimization result of maximum axial stiffness can be seen as quadrilateral embedded with an octagon, and material in the four corners is very thin. The cross-section is interpreted as an octagon embedded with cruciform structure if the four corners are removed. To achieve maximum lateral stiffness, the octagonal structure is obtained in consideration of loading direction and structural symmetry. Final simplified shape and cutting graph of front side rail are exhibited in Fig. 13.

Fig. 13
figure 13

Optimal cross-section and cutting graph of front side rail using static topology optimization

Full size image

It can be seen that the optimal cross-section is the combination of octagonal and cruciform structure. The join of cruciform structure contributes greatly to improving energy absorption capabilities and static stiffness including axial stiffness and lateral stiffness. If the optimal cross-section without cruciform structure is filled with re-entrant triangles structure, subjected force along inner re-entrant triangles will be partially or totally counteracted during impact compressive process, and the characteristics that shrinking under compression load will not occur, resulting in the decrease in energy absorption capabilities, as illustrated in Fig. 14. Owing to the existence of the cruciform structure, the octagonal structure is divided into four parts, each achieving superior performance of stiffness and energy absorption. Besides, use of symmetric re-entrant triangles will also enable the convenience of replacement. Although one or two filled re-entrant triangle structures may fail, the thin-walled tube still works in various loading and material cases. Hence, it is vitally meaningful to study this novel RTT.

Fig. 14
figure 14

Counterbalance of force along inner re-entrant triangles without cruciform structure

Full size image

5.3 Dynamic Topology Optimization of Thin-Walled Tube Without Re-entrant Triangles

On the basis of the static topology optimization, dynamic topology optimization of the tube without re-entrant triangles is executed. The optimized octagon shape of static topology optimization is utilized herein with a length of 300 mm. A rigid wall impacts the tube with mass of 1000 kg and initial velocity of 10 m/s. All the degrees of freedom at the bottom of this tube are constrained, and maximum effective energy absorption is no less than that of PST [28]. The materials used are consistent with that of static topology optimization. The model of the dynamic topology optimization is exhibited in Fig. 15.

Fig. 15
figure 15

Model of dynamic topology optimization

Full size image

The dynamic topology optimization model is carried out in LS-TaSC software; the optimal result is expressed in Fig. 16.

Fig. 16
figure 16

Optimal result of dynamic topology optimization

Full size image

Subsequently, dynamic topology optimization result is pruned. The outer contour retains octagon shape. The optimal shape is thin-walled structure with an inner quadrangle and an outer octagon, possessing capabilities of two-stage energy absorption. Eight rectangular induction slots with length of 20 mm and width of 5 mm are formed in the eight edges of the octagon at a distance of 15 mm from collision end, as exhibited in Fig. 17.

Fig. 17
figure 17

Finite element model of thin-walled tube without re-entrant triangles

Full size image

6 Analysis Results and Discussion

To validate the superiority of proposed optimization design method, the RTT designed based on the decoupling concept, NTT designed using traditional optimization method and PST are analyzed and compared in light of structural stiffness and energy absorption performance. To verify outstanding energy absorption capabilities of the proposed re-entrant triangles structure, RTT is compared with PFT herein. The most widely used filler with positive Poisson’s ratio and most excellent performance is aluminum foam [29]. Here, structural parameters of PFT are the same with that of RTT, and the density of filled foam is similar to that of re-entrant triangles. During simulation analysis, the foam material model is established based on the isotropic uniform material model proposed by Deshpande and Fleck [30, 31].

Figure 18 exhibits the specific structures of the four thin-walled tubes. Stiffness analysis and energy absorption comparisons are executed below.

Fig. 18
figure 18

Four types of thin-walled tubes

Full size image

6.1 Stiffness Analysis

All tubes are meshed with 2-mm hexahedral elements. Loading conditions and boundary conditions are the same as those of Fig. 12, and Table 4 exhibits the analysis results.

Table 4 Stiffness analysis results of four thin-walled tubes
Full size table

6.2 Energy Absorption Capabilities

In this paper, finite element models of PST and NTT are developed using HyperWorks software. The tubes are meshed with quadrilateral elements, with size of 5 mm. MAT 24 piecewise linear plasticity model is adopted to define the parameters of material AA6060T4. In crushing process, automatic single surface contact is applied on tube to prevent any interpenetration. The rigid wall impacts the tube with an initial velocity of \(V = 10\,{\text{m/s}}\); the bottom of tube is clamped with all degrees of freedom constrained, as illustrated in Fig. 19. The static and dynamic friction coefficients are set as 0.3 and 0.2, respectively. In addition, Fig. 20 exhibits analysis results of energy absorption for four thin-walled tubes and peak crush forces of the four tubes are obtained and compared in Table 5.

Fig. 19
figure 19

Impact models of PST and NTT

Full size image
Fig. 20
figure 20

Analysis results of energy absorption for four thin-walled tubes

Full size image
Table 5 Comparisons of peak crush force for four tubes
Full size table

It can be seen from above results that although traditional optimization design method can enhance the capabilities of energy absorption and reduce peak crush force effectively, structural stiffness is weakened, while the proposed decoupling method can improve both energy absorption and structural stiffness simultaneously. In comparison with positive Poisson’s ratio material, re-entrant triangles designed herein exhibit outstanding advantages in energy absorption. In the aspect of stiffness, RTT and PFT show little difference. The reason why lateral stiffness of RTT is slightly lower is that re-entrant triangles are possessed with anisotropic characteristics; stiffness along \(Y\) direction is higher than that along \(X\) direction. When the strain exceeds 0.57 and plateau stress increases, energy absorption of the RTT has been significantly enhanced. In comparison with the PFT, energy absorption of RTT increases by 17.23% and peak crush force reduces by 5.04%, which is mainly because the re-entrant triangles structure is more regular and impact deformation process is more stable relative to that of aluminum foam.

7 Conclusions

This paper takes front side rail to introduce decoupling thought. Filler re-entrant triangles are utilized to satisfy the requirements of energy absorption, and outer thin wall should meet high structural stiffness. This work initially exhibits theoretical models of re-entrant triangles in terms of relative density, equivalent elastic modulus and energy absorption. Then, experimental test is executed to validate the accuracy and reasonability of mechanical models. On this basis, the optimal geometric parameters of unit cell are achieved by utilizing NSGA-II method in terms of maximum unit volume energy absorption and minimum relative density.

The results show that the novel RTT designed based on decoupling thought can improve stiffness and energy absorption performance simultaneously. Compared with the positive Poisson’s ratio material, re-entrant triangles show superior advantages in energy absorption; this is mainly due to the plateau stress enhancement region. In comparison with PFT, energy absorption of RTT increases by 17.23% and peak crush force reduces by 5.04%. The results are encouraging in the sense that it offers another potential material for engineers to address the issue and the novel-type RTT with re-entrant triangles can be widely promoted and achieve further applications on new energy absorbent structures.