1 Introduction

Since the energy crisis and the serious environmental pollution are regarded as the greatest challenges for humanity in recent years. Renewable energy is increasingly being developed in different fields worldwide and in particular for electricity generation.

The electricity power system is accepted as one of the main sources of CO2 emissions, and therefore the development of renewable energy, which is considered to be non-polluting for generating electricity, has been a hot topic in recent years. Solar energy is recognized as the most promising renewable energy and is quickly being developed due to its advantages: inexhaustible supply, inexpensive and easy to maintain, etc.

Large-scale grid-connected photovoltaic (PV) systems have become a major development area for research although there are still many barriers, it is expected to have a major influence on the future grid [1]. More than 100 large-scale, above 10 MW, grid-connected PV plants have been built in the world and many countries are working on the 100 MW PV plants [2]. There are grid-connected PV systems and distributed network connected PV systems [3]. The grid-connected systems can also be divided into systems which can be dispatched and those which cannot. This is decided by whether or not the system is equipped with storage system [3].

In this paper, a large-scale dispatchable grid-connected PV system is proposed and simulated using MATLAB/Simulink. The storage system consists of both batteries and supercapacitors to achieve better performance. The simulation results verify the control strategy and main target of providing a constant power output, 10 MW, which is required by the grid for centralized dispatch.

2 System design and modeling

2.1 Structure of the system

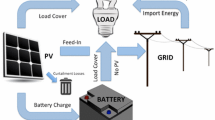
When the large-scale centralized PV system is connected with the grid, the grid should be able to regard it as a normal generation plant able to deliver a rated capacity and therefore be centrally dispatched [4]. Consequently, the PV plant should be equipped with an energy storage system in order that it can supply constant power to the grid all the time, including days and nights. This enables the PV plant to deliver power as required by the dispatcher instead of only supplying energy to the load when the sun shines.

A hybrid electricity storage of battery and supercapacitor has been selected in this paper with the target of providing a higher efficiency and better electricity quality. There are various devices which could be used for storage including batteries, flywheels, supercapacitors, and fuel cells (FC), all of which have different specific values of energy density and power density making them applicable for short-term or long-term energy storage [5].

The electrochemical battery, with its high energy density, is one of the most cost-effective energy storage devices, but its power density is relatively poor [6]. The supercapacitor, also called the electrical double layer capacitor, has a correspondingly high power density but low energy density. Subsequently, the complementary characteristics of batteries and supercapacitors make them an attractive choice for a hybrid electricity storage system in which the battery is chosen as the long-term storage device to meet the demand and the supercapacitor provides the short-term storage device to absorb the fast, high-frequency power fluctuations of the PV. Also, the supercapacitor can operate at any state of charge, since it stores energy by physically separating positive and negative charges, which means that it can be operated fully charged or fully discharged [7]. However, for the batteries, the state of charge SOC must be controlled to maintain an appropriate level to ensure a long cycle-life. The supercapacitor can therefore be used to protect the battery from short duration transients and help prolong the life of the battery. The hybrid electricity storage can therefore provide a better performance in terms of economy and generation efficiency [5].

2.2 System modeling

2.2.1 PV array

A PV cell is the smallest component within a PV plant which is used to build PV modules. The PV array consists of several PV modules in series or parallel. If N s is the number of the PV cells and N ss and N pp refer to the numbers of the PV modules in series and parallel respectively, the voltage of the PV array is N ss times the voltage of a PV module and the current capability is N pp times that of an individual cell. The equivalent circuit PV cell is shown in Fig. 1 and the mathematical model of the PV array is given in (1) [8, 9].

$$ I_{PV} = N_{pp} \left\{ {I_{ph} - I_{d} \left[ {exp\frac{{q\left( {\frac{{V_{PV} }}{{N_{s} N_{ss} }} + \frac{{I_{PV} R_{s} }}{{N_{pp} }}} \right)}}{AKT} - 1} \right] - \frac{{\frac{{V_{PV} }}{{N_{s} N_{ss} }} + \frac{{I_{PV} R_{s} }}{{N_{pp} }}}}{{R_{sh} }}} \right\}, $$
(1)

where I ph is photovoltaic current; I d is diode reversed saturation current; R s is equivalent series resistance of the PV array; Rsh is equivalent parallel resistance of the PV array; I PV is output current of the PV array; V PV is terminal voltage of the PV array; A is diode ideal factor of the P-N junction (dimensionless constant); K is Boltzmann constant (1.38×10−23 J/K); T is ambient temperature (°C); q is electronic charge (1.6×10−19 C).

Fig. 1
figure 1

Equivalent circuit of a PV cell

Full size image

The photovoltaic current, I ph , is dictated by several factors of which the solar irradiance and the ambient temperature are the most significant. The diode reversed saturation current, I d , is dependent on the diode characteristics. The values can be calculated by the (2) and (3).

$$ I_{ph} = \frac{S}{{S_{ref} }}\left[ {I_{ph,ref} + k_{o} \left( {T - T_{ref} } \right)} \right], $$
(2)
$$ I_{d} = I_{0} \left\{ {\left[ {\frac{{qU_{d} }}{AKT}} \right] - 1} \right\}, $$
(3)

where S is solar irradiance (W/m2); S ref is reference value of the solar irradiance (1000 W/m2); Iph,ref is reference value of photovoltaic current; k o is short-circuit current temperature coefficient related to the cell material; T ref is reference value of the ambient temperature (25°C or 273K); I0 is reversed saturation current through the P–N junction of the equivalent diode; and U d is terminal voltage of the equivalent diode.

It can be demonstrated that, using the mathematic equations above, the output of the PV system is affected by adverse weather conditions and behaves randomly. More importantly, the output has a nonlinear relationship with its principal influencing factors, irradiation and temperature.

2.2.2 Hybrid electricity storage

Although it is difficult to simulate the true behavior of the lead-acid battery, several models have been developed by researchers including the simple battery model and the Thevenin model [10]. Within the MATLAB/Simulink software, an existing battery model was chosen in which the type of battery and its significant parameters can be set easily. The structure of this existing model is very complex but the basic theory is based on the improved simple battery model whose equivalent circuit is shown in Fig. 2.

$$ R_{i} = \frac{{R_{0} }}{{S^{k} }}, $$
(4)
$$ S = 1 - \frac{\text{Ah}}{{C_{10} }}, $$
(5)
$$ V_{b} = E_{0} - I_{b} R_{i} , $$
(6)
$$ SOC = SOC_{0} - \frac{1}{{C_{b} }}\int\limits_{0}^{t} {I_{b} d_{\tau } } , $$
(7)

where R i is non-constant internal resistance; R0 is internal resistant when fully charged; Ah is unit of amp-hour; C10 is 10-h capacitor under the reference temperature (Ah); k is coefficient related to the capacitor and the discharge rate of battery; S is constant (equal to 0 when fully discharged and 1 when fully charged); V b is terminal voltage of the battery; E0 is voltage of the ideal voltage source; I b is current through the battery; SOC0 is initial state of charge (equal to 1 when fully charged); and C b is battery capacitor (Ah).

Fig. 2
figure 2

Equivalent circuit of the improved simple battery model

Full size image

When the battery is fully charged or fully discharged, the SOC is 100% or 0% respectively. In practical terms, the battery should never be fully discharged to ensure battery longevity. The minimum allowable SOC is typically about 20%.

Figure 3 shows the equivalent circuit of a basic supercapacitor in which the variable capacitance C plays the most important role and the resistance R2 describes the self-discharge of the supercapacitor. The capacitance C p together with the resistance R p represents the fast dynamic changes of the supercapacitor. C p is lower than C. The resistance R1 which is connected in series represents the energy loss during the charging or discharging period, while the resistance R3 is added in case of over-voltage. The variable capacitances C and C p should be chosen and regulated by the size the supercapacitor [11].

$$ i_{SC} \left( t \right) = C_{SC} \frac{d}{{d_{t} }}u_{SC} \left( t \right), $$
(8)

where i SC is current through supercapacitor; C SC is overall capacitance of supercapacitor; and u SC is terminal voltage of supercapacitor.

Fig. 3
figure 3

Equivalent circuit of the supercapacitor model

Full size image

2.2.3 Converters

In the SimPower Library of MATLAB/Simulink, there are models of inverters whose parameters and power electronic devices can be defined. The inverter is used to convert DC voltage into AC voltage. Consequently, the single-phase full-bridge inverter using insulated gate bipolar transistor (IGBT) and Diodes has been selected for this system.

The equivalent circuits of the Boost DC/DC converter and the Buck-Boost DC/DC converter are shown in Fig. 4. The Boost DC/DC converter is used to increase the input DC voltage. As a bi-directional converter, the Buck-Boost DC/DC converter has two operating modes as its name suggests. The two modes can be switched to regulate the duty of the MOSFET, as part of the control strategy. The capacitors are for filtering in other to obtain consequent output voltage V out . Attention has to be paid that the output voltage V out since it has an opposite polarity to the input voltage V in .

Fig. 4
figure 4

Circuits of Boost DC/DC converter and Buck-Boost DC/DC converter

Full size image

3 Control strategy

3.1 MPPT of the PV array

The maximum power point tracking (MPPT) of a PV system is an indispensable control to ensure that the PV array is working at the maximum power point no matter how the solar irradiation and ambient temperature change. The efficiency of the electricity generation of PV system can therefore be kept at a maximum.

Several MPPT algorithms have been proposed by previous researchers including the Perturb and Observe (P&O), the Constant Voltage tracking (CV) and the Incremental Conductance (INCond) [12]. Compared with other algorithms, the Incremental Conductance (INCond) has become the most widely used. It has many advantages; one being that the higher tracking accuracy can be maintained even when the weather conditions change rapidly [12]. Since there is no disturbance around the maximum power point, it is able to provide better stability than the P&O method with its additional perturbation. Accordingly, the INCond version of MPPT was chosen for the control strategy in this paper.

Since there is only one maximum power point on the P–V curve under fixed solar irradiation and ambient temperature, the gradient at that point is zero. Therefore, when the incremental conductance is equal to a negative value of the instantaneous conductance, the PV system is operating at the maximum power point. The basic mathematic theory is described by the following equations [12].

$$ \left\{ {\begin{array}{*{20}c} {P_{PV} = I_{PV} V_{PV} } \\ {\frac{{dP_{PV} }}{{dV_{PV} }} = I_{PV} + \frac{{dI_{PV} }}{{dV_{PV} }}V_{PV} = 0} \\ {\frac{{dI_{PV} }}{{dV_{PV} }} = - \frac{{I_{PV} }}{{V_{PV} }},} \\ \end{array} } \right. $$
(9)

where P PV is output power of PV array; I PV is output current of PV array; and V PV is output voltage of PV array.

The flow chart of the INCond is shown in Fig. 5. The output voltage and current of the PV array were constantly monitored and the values are compared with the previous ones. The incremental conductance is then compared with the negative value of the instantaneous conductance in order to find the point at which it satisfies (9). The reference value of PV array terminal voltage is then adjusted to the output of the MPPT control which is the reference voltage of PV array V ref . This is the voltage corresponding to the maximum power point. This is used as the input of a double-loop control to create the control signal for the DC/DC converter.

Fig. 5
figure 5

Flow chart of the INCond MPPT

Full size image

3.2 Control strategy of the battery

The battery is the main storage device and should supply enough power to ensure that the constant output power is provided to the grid. In particular, this is required during the evenings and cloudy days when there is no solar irradiation for the PV array.

When the output power of the PV system is higher than the required value, the surplus power is stored in the battery for later use.

The flow chart in Fig. 6 illustrates the control strategy for the battery. Based on the target power capacity, the first step is to monitor the difference, Pd, between the output power of the PV array, P PV , and the set output power, in this case which is 10 MW. When this is positive, there is surplus power which can be stored in the battery. When it is negative, power is required to be supplied from the battery to the grid.

Fig. 6
figure 6

Control strategy of the battery

Full size image

There are several operating modes of the battery during charging and discharging which are defined as constant current or constant voltage. In order to reduce the voltage fluctuation at the junction point, the battery should be switched to the required operating mode depending on the DC voltage, as shown in Fig. 6. The acceptable voltage fluctuation is 2% and the \( V_{DC}^{*} \) in the flow chart is the reference value for the DC link.

3.3 Control strategy for the supercapacitor

Due to the high power density and the low energy density, the discharging time of the supercapacitor is very short and its response is very fast. The supercapacitor plays the role of absorbing the high-frequency power fluctuations from the PV and maintaining the voltage of the DC link in a proper range. The random nature of these fluctuations is a key factor of the PV system and the instantaneous change in the output power is unpredictable. The supercapacitor always charges or discharges in a shorter time than the battery therefore the battery is protected from the high frequency fluctuations.

Figure 7 shows the control strategy for the supercapacitor. The voltage of the DC link is monitored and compared with the reference value, \( V_{DC}^{*} \), resulting in the error signal which is the input of the PI controller. The reference current of the supercapacitor, \( I_{SC}^{*} \), is used with the monitored supercapacitor current, I sc , to create the control signals for the Buck/Boost DC/DC converter through the current-tracking PWM.

Fig. 7
figure 7

Control strategy of the supercapacitor

Full size image

3.4 Special operation modes

The system’s set power output to be delivered to the grid is typically 50% of the rated power of the grid-connected PV plant in order to ensure a good performance. Other settings can be used dependant on the weather conditions. Generally, these operation modes can be classified into three modes according to the following equations.

$$ \left\{ {\begin{array}{*{20}c} {SOC = 20\% } \\ {0 < P_{PV} < 10,} \\ \end{array} } \right. $$
(10)
$$ \left\{ {\begin{array}{*{20}c} {SOC < 20\% } \\ {P_{PV} = 0,} \\ \end{array} } \right. $$
(11)
$$ \left\{ {\begin{array}{*{20}c} {SOC = 100\% } \\ {P_{PV} > 10.} \\ \end{array} } \right. $$
(12)

In the above equations, 20% is considered to be the acceptable lowest value of SOC of the battery. In the first mode based on (10), the power from the PV arrays is not enough to satisfy this requirement and the battery cannot supply the desired energy level due to its low SOC. Under this circumstance, the PV plant should be disconnected with the grid since the PV system cannot meet the desired power output for the grid. During this time, the PV plant is used to charge the battery until the SOC reaches a correspondingly high value when it can be switched to the normal operation mode.

As shown in (11), the second mode of operation, there is no output from the PV arrays and the battery cannot provide any output. The PV plant should be disconnected from the grid and left idle until good weather returns.

In the last mode, represented by (12), there is redundant solar energy which the battery cannot store since it is fully charged. Considering the proper design of the plant, this situation is considered rare. When this happens, the PV system should dump the redundant power into the grid, if possible. To ensure that the correct mode for the PV plant is used, the output power of the PV array and the SOC of the battery are continuously monitored.

4 Simulation results and discussion

The system has been modeled in MATLAB/Simulink. Weather data for one-year collected from a 100 MW PV plant in Qinghai province was used to provide irradiation patterns for two consequent days of operation to demonstrate the good performance of the system. The first day was a sunny day with adequate solar irradiation during the daytime and the second day was cloudy with much less sunshine. The control strategy of the grid-connected inverter was an important feature of the study and has been described in another research from [2]. This study focused on the performance of the DC power flows at the junction point providing the input of the grid-connected inverter, as shown in Fig. 8.

Fig. 8
figure 8

Structure of the large-scale dispatchable grid-connected PV system

Full size image

The output power of the PV system for the two days of the test is shown in Fig. 9. The output power in the first sunny day was much higher than that for the second cloudy day. The output power follows that of the solar irradiation derived from the weather data. This demonstrates the good performance of the MPPT control function.

Fig. 9
figure 9

Output power of the PV system

Full size image

During the first day, the peak output power from the PV array was higher than the set power output level. During the second day, however, it was lower than the set level. The surplus during the first day was redundant power and was stored in the storage system. During the second day, power was required to be supplied from the storage.

The SOC of the battery during the two days is shown in Fig. 10. The initial SOC was 100%, showing that the battery was fully charged at the beginning of the test. During the first day, the battery was first discharged until sunrise and then almost fully charged again at around noon due to the high output power of the PV system. During the second day, the battery is continually discharging because of the shortage of the solar irradiation.

Fig. 10
figure 10

SOC of the battery

Full size image

The differences in the SOC are due to the different discharging or charging current according to the system’s operation mode. Figure 11 illustrates the current through the supercapacitor during the two days. The positive current represents the discharging of the supercapacitor and vice versa.

Fig. 11
figure 11

Current through the supercapacitor

Full size image

In order to test the quality of supply at the DC link, the DC voltage V DC was monitored as shown in Fig. 12. It is presented in per unit values, p.u. The simulation results show that the DC voltage was maintained at around the reference value with only small fluctuations. There was an obvious error at the start of the simulation and this was attributed to settling down of the simulation algorithms. It shows the stability in the DC power prior to input to the grid-connected inverter. A higher level of functions was expected as a result of the influence on grid on the PV system [13].

Fig. 12
figure 12

Voltage of the DC link

Full size image

5 Conclusions

With the development of the renewable technologies, large-scale grid-connected PV plant has become a hot topic.

The conclusions are:

  1. 1)

    A centralized, large-scale grid-connected PV system with a battery-supercapacitor hybrid electricity storage has been described. Taking advantage of their complementary characteristics, the batteries and supercapacitors have been used as the main and secondary storage devices to provide a high quality of supply and efficiency. The PV system was modeled in the MATLAB/Simulink and the control strategies demonstrated.

  2. 2)

    Two sets of weather data were collected from an existing PV site and used as the input for the system to demonstrate its feasibility. The first day was sunny, while the second was cloudy.

  3. 3)

    The simulation studies demonstrated that the proposed system could operate smoothly over the 48 hours test period. Using the storage system, the PV system was able to supply a continuous 10 MW of power to the grid as set by the centralized dispatch schedule. This was achieved for both the sunny and the cloudy day. The voltage of the DC link was maintained within an acceptable range.