A robust optimization model for distribution and evacuation in the disaster response phase

Abstract

Natural disasters, such as earthquakes, affect thousands of people and can cause enormous financial loss. Therefore, an efficient response immediately following a natural disaster is vital to minimize the aforementioned negative effects. This research paper presents a network design model for humanitarian logistics which will assist in location and allocation decisions for multiple disaster periods. At first, a single-objective optimization model is presented that addresses the response phase of disaster management. This model will help the decision makers to make the most optimal choices in regard to location, allocation, and evacuation simultaneously. The proposed model also considers emergency tents as temporary medical centers. To cope with the uncertainty and dynamic nature of disasters, and their consequences, our multi-period robust model considers the values of critical input data in a set of various scenarios. Second, because of probable disruption in the distribution infrastructure (such as bridges), the Monte Carlo simulation is used for generating related random numbers and different scenarios; the p-robust approach is utilized to formulate the new network. The p-robust approach can predict possible damages along pathways and among relief bases. We render a case study of our robust optimization approach for Tehran’s plausible earthquake in region 1. Sensitivity analysis’ experiments are proposed to explore the effects of various problem parameters. These experiments will give managerial insights and can guide DMs under a variety of conditions. Then, the performances of the “robust optimization” approach and the “p-robust optimization” approach are evaluated. Intriguing results and practical insights are demonstrated by our analysis on this comparison.

Introduction

Prolonged and stressful situations, such as famine or unexpected disasters, such as earthquakes and fatal diseases, are known as humanitarian crises (Kress 2016). Among humanitarian crises, earthquakes are one of the most dangerous occurrences. The Kathmandu earthquake in Nepal on April 26, 2015, produced a force equal to 20 thermonuclear weapons. The Izmit earthquake in Turkey on August 17, 1997 displaced more than 300,000 people from their homes. The Rudbar earthquake in Iran on June 21, 1990 destroyed 700 villages throughout the cities of Rudbar, Manjill, and Lushan; the cost in damages was a staggering $200,000,000. These are only few examples of the worst earthquakes in Earth’s history. About 300 million people are affected by earthquakes per year. In addition, the annual costs of this natural disaster are about 0.17 of the world’s GDP (Guha-Sapir 2014). Disaster management provides powerful approaches to cope with humanitarian crises. After the Indian Ocean tsunami on December 26, 2004, humanitarian logistics in disaster management attracted researcher’s attention (Jahre et al. 2007) and the vital role of logistics in humanitarian crises became was undeniable (Christopher and Tatham 2014). For an effective response after disasters, an optimized logistics network will require perfectly synthesized relationships between all the players involved (Cozzolino 2012). However, logistics services are expensive, and the estimates reveal that they hover around 80 % of the total cost of disaster relief (Wassenhove 2006). For instance, it has been calculated that the logistical cost of the Nicaragua earthquake in 1792 was about 35 % of the country’s entire GDP.

Effective distribution of the first aid commodities, medicals, and blood supplies, management of inventory level of these products, evacuation, and transportation are major provocations (Cozzolino 2012). For example, earthquakes usually cause enough damage to some of the transportation infrastructure that it often renders them unusable and/or inaccessible. This creates varied challenges in regard to distribution and evacuation systems (Ahmadi et al. 2015).

The latter mentioned instances demonstrate the complexity of humanitarian logistics and the need for the permanent, yet ever evolving, implementation of an ingenious design plan, and execution of logistics networks before, during, and after natural disasters strike. Several factors impact this complexity. Large demands for relief products and related uncertainties are major problems (Lin 2010). As long as disaster relief systems have a short life cycle, time plays a significant role due to nature of rescue operations (Oloruntoba and Gray 2006). To address the importance of time allocation throughout a rescue operation (Walton et al. 2011), speed is considered a high priority factor in elevating the flow of distribution and evacuation operations. Another equally important factor is the possible damage among relief bases and pathways that may challenge the effectiveness of disaster efforts (Tzeng et al. 2007). Last, but not least, is the factor that demand for relief products after disasters exhibits a dynamic behavior. During the first hours after a disaster hits, the affected areas need more products and services, but the demand for these products and services decreases as time elapses (Jabbarzadeh et al. 2014).

According to the four phases of disaster management (mitigation, preparedness, response, and recovery), the proposed model in this study pertains to the preparedness as well as the response phase. Therefore, in consideration of the aforementioned uncertainty and dynamic nature of humanitarian logistics, this study develops a dynamic optimization model using a robust stochastic approach. The model will determine the number of relief bases needed and the optimal locations of these bases, and it guides the decision-making process of distribution and evacuation decisions during the response phase. Disaster affected areas, relief bases, emergency tents, and hospitals are considered key components in this research. The objective of this network model is to minimalize the total cost of disaster management by considering components, such as fixed, transportation, inventory, and product shortages. While our model has considered real situations, its design will help decision makers to implement their choices of location and allocation during the response phase of disaster management.

The remainder of this paper is organized as follows:

• Section “Literature review” reviews optimization research in humanitarian logistics.

• Section “Problem description” presents the considered problems in two parts. In the first part, the robust model is provided, and in the second part, the p-robust model is shared. In addition, basic assumptions of the proposed models are defined.

• Section “Computational result and discussion” reveals the numerical results of both the models. In addition, this section provides comparisons in performance between the robust and p-robust model.

• Section “Conclusion and future research” offers concluding remarks and gives some directions for future research in this manner.

Literature review

Necessary commodities and materials should be delivered immediately after an earthquake. An aid distribution plan is essential to deliver necessary commodities, such as food, medicine, provisions for sanitation, shelter, and water to sustain human life and to administer the total costs. In addition, injured people need to be transported to emergency tents and hospitals in a timely fashion. In fact, humanitarian logistics, as an efficient plan for aid distribution and evacuation after earthquakes, can significantly diminish the death rate and total operational costs. Humanitarian logistics as a part of humanitarian aid and disaster management has become an important area for researchers. Jahre et al. (2007), Altay and Green (2006), Özdamar and Ertem (2015), and Caunhye et al. (2012) have provided overviews on humanitarian logistics. Our literature on disaster relief is divided into two classifications: deterministic and uncertain models in humanitarian logistics.

Deterministic programming in humanitarian logistics

The study of disaster management originated with the large-scale industrial and environmental disasters in the 1980s (Shrivastava et al. 1988). Logistics in providing the most important types of commodities and services were the main theme of the research during this period. A multi-objective linear model that aims to minimize transportation cost and maximize the demand for food was proposed by (Knott 1987). He developed a vehicle-routing model in his next study which aimed to maximize the amount of delivered food (Knott 1988). Barbarosoğlu et al. (2002) presented a hierarchical model in disaster relief using helicopters for rescue operations during natural disasters. Their research has helped DMs to make vehicle-routing and transportation decisions during the response phase. An emergency logistics model aimed to determine distribution decisions of relief commodities was developed by Özdamar et al. (2004). They designed a multi-objective model about relief delivery systems (Tzeng et al. 2007). The most momentous factor in their research was enhancing the performance of the distribution of relief materials. Their model minimized total cost and travel time and maximized the minimal satisfaction. In addition, Nolz et al. (2011) established a multi-objective model for the response phase to minimize the risk and total travel time and maximize the coverage. They considered correlated and uncorrelated risk measures to cope with both earthquake and flood risks. Another multi-objective model which minimizes the total unsatisfied demand and total travel time was developed by Lin et al. (2011) that consider different types of vehicles and relief commodities. Afshar and Haghani (2012) proposed a single-objective model to schedule the flow of commodities and locate facility positions. Their research also considered the routing problem to increase effective response. Finally, Barzinpour and Esmaeili 2014a developed a multi-objective relief chain location distribution model for the preparedness phase of disaster management. Their model aimed to maximize the coverage and minimize total costs.

Some researchers applied transportation in different ways. For some examples, Fiedrich et al. (2000) presented a relief network to transport injured people and allocate resources to them. In addition, a dynamic model to evacuate injured people and satisfy the demands of relief commodities was introduced by Yi and Özdamar (2007). Likewise, Yi and Kumar (2007), Ozdamar (2011), and Özdamar and Demir (2012) proposed a mathematical model for transporting injured people from affected areas to medical centers and delivering relief commodities to victims in the response phase.

Uncertainty programming in humanitarian logistics

Although dynamic multi-period and multi-period models helped DMs during and after disasters, they did not capture the uncertain nature of disasters. Many researchers started considering this uncertainty in disaster relief planning in their studies. Some of them used stochastic programming to distribute relief commodities through probable scenarios. Barbarosoğlu and Arda (2004) used scenario planning in a two-stage stochastic model for the response phase of an earthquake. In addition, Jotshi et al. (2009) used robust optimization to schedule routes for vehicles after the disaster. To minimize the maximum rescue time based on all scenarios, a robust model for a disaster network with uncertainty in distances between nodes was proposed by Ma et al. (2010). A stochastic optimization in the preparedness phase of disaster management was proposed to determine the storage locations of medical supplies and requested inventory amounts for each type of medical supply. Mete and Zabinsky (2010) and Salmerón and Apte (2010) proposed a two-stage stochastic programming in preparedness and response phases. In the first stage, they determined “aid-prepositioning” and the second-stage specified distribution decisions. Another study was done by Rawls and Turnquist (2010). They presented a two-stage stochastic programing for location and distribution of emergency commodities under uncertain demand. According to uncertainty in demand and the availability of pathways and supply of relief commodities, Zhan and Liu (2011) considered a location-allocation problem using chance constraint programming to minimize expected travel time and unsatisfied demands. Najafi et al. (2013) developed a multi-objective, multi-mode, multi-commodity, and multi-period stochastic model to manage the logistics of both commodities and injured people in the earthquake response phase. Another robust disaster relief logistics network with perishable commodities was proposed by Rezaei-Malek et al. (2016) which used a scenario-based robust stochastic approach. This research aimed to determine the optimum location-allocation and distribution plan, along with the best ordering policy for restocking perishable commodities at the pre-disaster phase. Ahmadi et al. (2015) presented a two-stage stochastic program which was an operational location-routing problem (LRP) and could be used after an earthquake in the response phase. They tried to make vehicle-routing and distribution decisions about a real situation. Finally, Tofighi et al. (2016) developed a novel, two-stage scenario-based model to determine the location of central warehouses and local distribution centers. In addition, this research considered the distribution plan and availability level of the transportation network’s routes.

The above paragraphs show several models that have been proposed for the preparedness and the response phase of disaster management, but most of these models do not consider unforeseen constraints and misassumptions that DMs face in real disasters. For example, a variety of vehicles are needed to evacuate the injured and to transport relief commodities to affected areas. In addition, most of the models do not consider possible disruptions in the transportation system during earthquakes which challenge distribution and evacuation operations. In addition, most models typically only utilize permanent facilities and medical centers, however, during a real disaster, the majority of injures could be treated in temporary centers, such as emergency tents. Consequently, these temporary medical posts will lower congestion and overcrowding in permanent treatment centers. Hence, the previous model research studies may be considered to be incomplete or impractical during natural disasters.

We developed this research paper based on Barzinpour and Esmaeili (2014b) and Bozorgi-Amiri et al. (2013). The model proposed in Bozorgi-Amiri et al. (2013) does not consider the logistics of injures. However, we believe that one of the most important actions taken during an earthquake occurrence is evacuating the injured from the affected areas. In addition, they did not consider the dynamic nature of disaster. As a result, this model only heeded one time period. Nevertheless, according to Jabbarzadeh et al. (2014), demands for blood products and other commodities immediately following a disaster are higher than they are in later stages. Therefore, a dynamic model should be developed to solve this problem. Moreover, in real-world disasters and rescue operations, Hilal Ahmar and other organizations can use their temporary facilities in affected areas to minimize total costs and to maximize effectiveness. In Bozorgi-Amiri et al. (2013) scenarios that only utilize permanent facilities, the results can be misleading. Barzinpour and Esmaeili (2014b) introduced a multi-objective relief chain model. Their research neither considered the evacuation operation nor the dynamic nature of natural disasters. Besides, inverse to our modus operandi (Barzinpour and Esmaeili 2014b), it did not consider the uncertain nature of natural disasters and possible disruptions along pathways and among relief bases. Finally, it is remarkable that both models neither considered the medical centers (such as hospitals that can facilitate life and death situations) nor different types of vehicles to transport injured patients and relief commodities.

Therefore, our three contributions of this study are summarized as follows:

• Because of the uncertain nature of natural disasters which causes a difficult situation for DMs during and after disasters, we developed a model which considers various sources of uncertainty.

• Developing a dynamic robust optimization model which contemplates possible disruptions along pathways and among relief bases.

• Applying the model to a real-world disaster relief chain devoted to the supply of relief commodities and blood supplies to affected areas, and the evacuation of injured people to medical centers.

Our model aims to determine the optimal number of relief bases needed as well as the optimal locations of said bases. In addition, it specifies the number and location of emergency tents in affected areas that serve as temporary triage and treatment centers and as distribution centers for relief commodities. In addition, this model considers the urgent transportation need of the injured to permanent hospitals when necessary. The objective function in our robust model minimizes total costs, such as fixed, transportation, operation, and inventory. Moreover, we propose a p-robust model which considers possible disruptions along pathways and among relief bases using the Monte Carlo simulation to generate random numbers and different scenarios.

Problem description

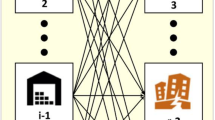
To address Fig. 1, we consider four stages in this humanitarian logistics network. The first stage shows relief bases, the second one contains emergency tents, the third stage is the set of affected areas, and the last stage consists of hospitals. We must mention that the location of relief bases is partly determined by their distances from the affected areas and their maximum storage capacity for relief commodities and rescue vehicles. As long as they are under the authority of Hilal Ahmar in Iran, relief bases will have emergency tents, thus the total cost of this network is significantly reduced by locating emergency tents in the affected areas. These emergency tents provide triage, first aid, and blood transfusions under normal conditions, but in emergency situations, the injured should be carried to the fourth stage hospitals. In this section, we provide our mathematical models. First, we present a robust optimization formulation and its related model that incorporates different disaster scenarios for the values of critical input data. Then, we introduce the p-robust model that incorporates different scenarios for possible disruptions after an earthquake occurrence.

Fig. 1

General plan of humanitarian logistics

Robust model

Mulvey et al. 1995 introduced a robust optimization with optimal design of the supply chain in the real world and uncertain environments. By expressing the values of vital input data in a set of scenarios, robust optimization tries to approach the preferred risk aversion. This approach results in a series of solutions that are less sensitive to the model data from a scenario set. Two sets of variables act in this approach control and design variables. The first set is subject to adjustment once a specific realization of the data is obtained. In the second set, design variables cannot be adjusted once uncertain and random parameters are observed. Constraints can be divided into two types as well, namely structural and control constraints. Structural constraints are typical linear programming constraints which are free of uncertain parameters, while the coefficients of control constraints are subject to uncertainty.

Here, we formulate a robust optimization model for distribution and evacuation in the disaster response phase. This multi-period model determines the following decisions at each period:

• 1. The number and location of relief bases;

• 2. The number of rescue vehicles in each relief base;

• 3. The number and location of emergency tents;

• 4. The quantity of relief commodities and blood supplies which are transported to emergency tents;

• 5. The number of injured people that are carried to hospitals.

Before introducing the mathematical model, we present the following assumptions on this model:

• 1. Emergency tents can be moved at the end of each stage.

• 2. Demand for relief commodities and blood supplies can be satisfied by more than one emergency tent.

• 3. Distribution possibilities can be determined by experts per scenario.

• 4. Each affected area may be served by either emergency tents or relief bases.

With these assumptions, our dynamic model minimizes total cost and determines the above decisions. We assume that the first-stage parameters and decision variables, such as fixed cost, are determined, because relief bases are already in place long before the onset of a disaster. However, in the second stage, respect to the specific scenarios, decision variables and some of their parameters are uncertain, such as demand for each relief commodity in each period.

The following notations are used to design the proposed stochastic model:

Indices

I :

Set of affected areas indexed by i є {1, 2, …, I}

J :

Set of candidate locations for relief bases indexed by j є {1, 2, …, J}

N :

Set of candidate locations for emergency tents indexed by n, m є {1, 2, …, N}

P :

Set of required blood supplies indexed p є {1, 2, …, P}

Q :

Set of required commodities indexed q є {1, 2, …, Q}

Z :

Set of required drugs indexed by z є {1, 2, …, Z}

K :

Set of hospitals indexed by k є {1, 2, …, K}

L :

Set of rescue vehicles indexed by ℓ є {1, 2, …, L}

T :

Set of time periods indexed by t є {1, 2, …, T}

S :

Set of disaster scenarios indexed by s є {1, 2, …, S}

Parameters

$f_{j}$ :

Fixed cost of locating an emergency tent belongs to relief base j

$f_{j}^{\prime }$ :

Fixed costs of locating a relief base at location j

$B_{nm}^{st}$ :

Cost of moving an emergency tent from location m to location n in period t under scenario s

$\beta_{z}^{ts}$ :

Unit operational cost of equipping an emergency tent with drug z in period t under scenario s

$\beta_{p}^{\prime ts}$ :

Unit operational cost of equipping an emergency tent with blood supply p in period t under scenario s

$\beta_{l}^{\prime \prime ts}$ :

Unit operational cost of equipping a relief base with rescue vehicle ℓ in period t under scenario s

$\beta_{q}^{\prime \prime \prime ts}$ :

Unit operational cost of equipping a relief base with commodity q in period t under scenario s

$W_{z}^{ts}$ :

Unit transportation cost of drug z in period t under scenario s

$W_{p}^{\prime ts}$ :

Unit transportation cost of blood supply p in period t under scenario s

$W_{l}^{\prime \prime ts}$ :

Unit transportation cost of rescue vehicle ℓ in period t under scenario s

$W_{q}^{\prime \prime \prime ts}$ :

Unit transportation cost of commodity q in period t under scenario s

r :

Coverage radius of emergency tents

$r_{q}^{\prime }$ :

Coverage radius of relief bases for commodity q

$d_{jn}$ :

Distance between relief base j and emergency tent n

$d_{in}$ :

Distance between affected area i emergency tent n

$d_{ij}^{{}}$ :

Distance between affected area i and relief base j

$d_{ik}$ :

Distance between affected area i and hospital k

$h_{z}^{{}}$ :

Unit holding cost of drug z in an emergency tent

$h_{p}^{\prime }$ :

Unit holding cost of blood supply p in an emergency tent

$h_{q}^{\prime \prime \prime }$ :

Unit holding cost of commodity q in a relief base

$C_{zj}$ :

Initial inventory of drug z in relief base j

$C_{pj}^{\prime }$ :

Initial inventory of blood supply p in relief base j

$p_{s}$ :

Probability of scenario s occurrence

$T_{i}^{ts}$ :

Available time to finish rescue operations at affected area i in period t under scenario s

$\lambda_{jl}$ :

Increasing in coverage radius of relief base j by adding one more rescue vehicle ℓ

$V_{l}$ :

Average velocity of rescue vehicle ℓ

$g_{l}$ :

Capacity of rescue vehicle ℓ

M :

A very large number

$U_{z}$ :

Capacity of an emergency tent for drug z

$U_{p}^{\prime }$ :

Capacity of an emergency tent for blood supply p

$U_{q}^{\prime \prime \prime }$ :

Capacity of an emergency tent for commodity q

$m_{j}$ :

Available emergency tents in relief base j

$D_{iz}^{ts}$ :

Demand of affected area i for drug z in period t under scenario s

$D_{ip}^{\prime ts}$ :

Demand of affected area i for blood supply p in period t under scenario s

$D_{i}^{\prime \prime ts}$ :

Number of injured people at affected area i in period t under scenario s

$D_{iq}^{\prime \prime \prime ts}$ :

Demand affected area i for commodity q in period t under scenario s

Decision variables

$A_{j}$ :

If a relief base is located at site j equal to 1, otherwise 0

$\eta_{jlik}^{ts}$ :

If rescue vehicle ℓ from relief base j is assigned to affected area i and hospital k in period t and under scenario s equal to 1, otherwise 0

$A_{jqi}^{\prime \;ts}$ :

If relief base j is assigned to affected area i to cover demand of commodity q in period t under scenario s equal to 1, otherwise 0

$A_{jqi}^{\prime \prime ts}$ :

Quantity of commodity q transported from relief base j to affected area i in period t under scenario s

$S_{jl}^{ts}$ :

Coverage radius of rescue vehicle ℓ at relief base j in period t under scenario s

$x_{nj}^{ts}$ :

If an emergency tent belongs to relief base j is located at site n in period t under scenario s equal to 1, otherwise 0

$Z_{nmj}^{ts}$ :

If an emergency tent from relief base j is located at location m in period t − 1 and moves to location n in period t under scenario s equal to 1, otherwise 0

$x_{njzi}^{\prime ts}$ :

If an emergency from relief base j at point n is assigned to affected area i to cover demand of drug z in period t under scenario s equal to 1, otherwise 0

$x_{njzi}^{\prime \prime ts}$ :

Quantity of drug z transported from emergency tent n, belongs to relief base j, to affected area i in period t under scenario s

$y_{njpi}^{\prime ts}$ :

If an emergency from relief base j at point n is assigned to affected area i to cover demand of blood supply p in period t under scenario s equal to 1, otherwise 0

$y_{njpi}^{\prime \prime ts}$ :

Quantity of blood supply p transported from emergency tent n, belongs to relief base j, to affected area i in period t under scenario s

$I_{njz}^{ts}$ :

Inventory level of drug z at emergency tent n which belongs to relief base j at the end of period t under scenario s

$I_{njp}^{\prime ts}$ :

Inventory level of blood supply p at emergency tent n which belongs to relief base j at the end of period t under scenario s

$I_{jq}^{\prime \prime \prime ts}$ :

Inventory level of commodity q at relief base j at the end of period t under scenario s

$\delta_{iz}^{ts}$ :

Unsatisfied demand of drug z at affected area i in period t under scenario s

$\delta_{ip}^{\prime ts}$ :

Unsatisfied demand of blood supply p at affected area i in period t under scenario s

$\delta_{i}^{\prime \prime ts}$ :

Uncovered injuries at affected area i in period t under scenario s

$\delta_{iq}^{\prime \prime \prime ts}$ :

Unsatisfied demand of commodity q at affected area i in period t under scenario s

Now, we formulate a multi-period, robust network based on Mulvey et al. (1995). The objective function of the proposed model consists of five components:

The fixed cost of locating relief bases and emergency tents (FCs), the cost of moving emergency tents (VCs), the operational cost of supplying relief commodities, blood supplies and rescue vehicles (OCs), the transportation cost for distributing and evacuating (TCs), and inventory cost associated with the storage of relief commodities and blood supplies (ICs).

$$ {\text{FC}}_{\text{s}} = \sum\limits_{n \in N} {\sum\limits_{j \in J} {\sum\limits_{t \in T} {f_{j} x_{nj}^{ts} } } } + \sum\limits_{j \in J} {f_{j}^{\prime } A_{j} } $$

(1)

$$ {\text{VC}}_{\text{s}} = \sum\limits_{n \in N} {\sum\limits_{m \in N} {\sum\limits_{j \in J} {\sum\limits_{t \in T} {B_{nm}^{ts} Z_{nmj}^{ts} } } } } $$

(2)

$$ \begin{aligned} {\text{OC}}_{\text{s}} = \sum\limits_{n \in N} {\sum\limits_{z \in Z} {\sum\limits_{j \in J} {\sum\limits_{i \in I} {\sum\limits_{t \in T} {\beta_{z}^{ts} x_{njzi}^{\prime \prime ts} } } } } } + \sum\limits_{n \in N} {\sum\limits_{j \in J} {\sum\limits_{p \in P} {\sum\limits_{i \in I} {\sum\limits_{t \in T} {\beta_{p}^{\prime ts} y_{njpi}^{\prime \prime ts} } } } } } \hfill \\ + \sum\limits_{j \in J} {\sum\limits_{k \in K} {\sum\limits_{l \in L} {\sum\limits_{i \in I} {\sum\limits_{t \in T} {\beta_{l}^{\prime \prime ts} \eta_{jlik}^{ts} } } } } } + \sum\limits_{q \in Q} {\sum\limits_{j \in J} {\sum\limits_{i \in I} {\sum\limits_{t \in T} {\beta_{q}^{\prime \prime \prime ts} A_{jqi}^{\prime \prime ts} } } } } \hfill \\ \end{aligned} $$

(3)

$$ {\text{TC}}_{\text{s}} = \sum\limits_{n \in N} {\sum\limits_{z \in Z} {\sum\limits_{j \in J} {\sum\limits_{i \in I} {\sum\limits_{t \in T} {(d_{in} + d_{jn} )W_{z}^{ts} x_{njzi}^{\prime \prime ts} } } } } } + \sum\limits_{n \in N} {\sum\limits_{p \in P} {\sum\limits_{j \in J} {\sum\limits_{i \in I} {\sum\limits_{t \in T} {(d_{in} + d_{jn} )W_{p}^{\prime ts} y_{njpi}^{\prime \prime ts} } } } } } + \sum\limits_{j \in J} {\sum\limits_{l \in L} {\sum\limits_{k \in K} {\sum\limits_{i \in I} {\sum\limits_{t \in T} {(d_{ij} + d_{ik} )W_{l}^{\prime \prime ts} \eta_{jlik}^{ts} } } } } } + \sum\limits_{j \in J} {\sum\limits_{q \in Q} {\sum\limits_{i \in I} {\sum\limits_{t \in T} {d_{ij} W_{q}^{\prime \prime \prime ts} A_{jqi}^{\prime \prime ts} } } } } $$

(4)

$$ {\text{IC}}_{\text{s}} = \sum\limits_{z \in Z} {\sum\limits_{j \in J} {\sum\limits_{n \in N} {\sum\limits_{t \in T} {h_{z}^{ts} I_{njz}^{ts} } } } } + \sum\limits_{p \in P} {\sum\limits_{j \in J} {\sum\limits_{n \in N} {\sum\limits_{t \in T} {h_{z}^{\prime ts} I_{njp}^{\prime ts} } } } } + \sum\limits_{q \in Q} {\sum\limits_{j \in J} {\sum\limits_{t \in T} {h_{q}^{\prime \prime \prime ts} I_{jq}^{\prime \prime \prime ts} } } }. $$

(5)

Based on above cost components, we formulate the proposed model:

Min

$$ \sum\limits_{s \in S} {p_{s} ({\text{FC}}_{s} + {\text{VC}}_{s} + {\text{OC}}_{s} + {\text{TC}}_{s} + {\text{IC}}_{s} )} + \lambda \,\sum\limits_{s \in S} {p_{s} [({\text{FC}}_{s} + {\text{VC}}_{s} + {\text{OC}}_{s} + {\text{TC}}_{s} + {\text{IC}}_{s} ) - \sum\limits_{{s^{\prime } \in S}} {p_{{s^{\prime } }} ({\text{FC}}_{{s^{\prime } }} + {\text{VC}}_{{s^{\prime } }} + {\text{OC}}_{{s^{\prime } }} + {\text{TC}}_{{s^{\prime } }} + {\text{IC}}_{{s^{\prime } }} )} + 2\theta_{s} ]} + \omega {\mkern 1mu} \sum\limits_{I \in I} {\sum\limits_{z \in Z} {\sum\limits_{t \in T} {p_{s} \delta_{iz}^{ts} } } } + \omega^{\prime } {\mkern 1mu} \sum\limits_{I \in I} {\sum\limits_{z \in Z} {\sum\limits_{t \in T} {p_{s} \delta_{ip}^{{\prime {\kern 1pt} ts}} } } } + \omega^{\prime } {\mkern 1mu} \sum\limits_{I \in I} {\sum\limits_{z \in Z} {\sum\limits_{t \in T} {p_{s} \delta_{i}^{\prime } } } } + \omega^{\prime \prime } {\mkern 1mu} \sum\limits_{I \in I} {\sum\limits_{z \in Z} {\sum\limits_{t \in T} {p_{s} \delta_{iq}^{\prime \prime ts} } } }. $$

(6)

Subject to:

$$ \sum\limits_{j \in J} {x_{nj}^{ts} } + \sum\limits_{j \in J} {\sum\limits_{m \in N} {Z_{nmj}^{ts} } } \le 1\quad\forall n \in N,\quad\forall t \in T,\quad\forall s \in S $$

(7)

$$ \sum\limits_{j \in J} {\sum\limits_{m \in N} {Z_{mnj}^{ts} } } \le \sum\limits_{j \in J} {\sum\limits_{m \in N} {Z_{nmj}^{t - 1\,s} } } + \sum\limits_{j \in J} {x_{nj}^{t - 1s} } \quad\forall n \in N,\quad\forall t \in T,\quad\forall s \in S $$

(8)

$$ \sum\limits_{t \in T} {\sum\limits_{n \in N} {x_{nj}^{ts} } \le m_{j} } \quad\forall j \in J,\quad\forall t \in T,\quad\forall s \in S $$

(9)

$$ d_{in} x_{injzi}^{\prime ts} \le r\quad\forall z \in Z,\quad\forall j \in J,\quad\forall n \in N,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S $$

(10)

$$ d_{in} y_{injpi}^{\prime ts} \le r\quad\forall p \in P,\quad\forall j \in J,\quad\forall n \in N,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S $$

(11)

$$ 1 - \sum\limits_{j \in J} {x_{nj}^{ts} } - \sum\limits_{j \in J} {\sum\limits_{m \in N} {Z_{nmj}^{ts} } } \ge \sum\limits_{j \in J} {x_{nj}^{t + 1\,s} } + \sum\limits_{j \in J} {\sum\limits_{m \in N} {Z_{nmj}^{t + 1\,s} } } \quad\forall n \in N,\quad\forall t \in T,\quad\forall s \in S $$

(12)

$$ \sum\limits_{n \in N} {\sum\limits_{j \in J} {I_{nkj}^{t - 1\,s} } } - \,\sum\limits_{n \in N} {\sum\limits_{j \in J} {I_{nkj}^{ts} } } + \delta_{iz}^{ts} + \sum\limits_{n \in N} {\sum\limits_{j \in J} {x_{njzi}^{\prime \prime ts} } } = D_{iz}^{ts} \quad\forall i \in I,\quad\forall z \in Z,\quad\forall t \in T,\quad\forall s \in S $$

(13)

$$ \sum\limits_{n \in N} {\sum\limits_{j \in J} {I_{njp}^{\prime t - 1\,s} } } - \,\sum\limits_{n \in N} {\sum\limits_{j \in J} {I_{njp}^{\prime ts} } } + \delta_{ip}^{\prime ts} + \sum\limits_{n \in N} {\sum\limits_{j \in J} {y_{njpi}^{\prime\prime ts} } } = D_{ip}^{\prime ts} \quad\forall i \in I,\quad\forall p \in P,\quad\forall t \in T,\quad\forall s \in S $$

(14)

$$ x_{nj}^{ts} \le A_{j} \quad\forall n \in N,\quad\forall j \in J,\quad\forall t \in T,\quad\forall s \in S $$

(15)

$$ x_{njzi}^{\prime ts} \le \left(x_{nj}^{ts} + \sum\limits_{m \in N} {Z_{nmj}^{ts} } \right)\quad\forall n \in N,\quad\forall j \in J,\quad\forall i \in I,\quad\forall z \in Z,\quad\forall t \in T,\quad\forall s \in S $$

(16)

$$ y_{njpi}^{\prime ts} \le \,\left(x_{nj}^{ts} + \sum\limits_{m \in N} {Z_{nmj}^{ts} } \right)\quad\forall n \in N,\quad\forall j \in J,\quad\forall i \in I,\quad\forall p \in P,\quad\forall t \in T,\quad\forall s \in S $$

(17)

$$ x_{njzi}^{\prime\prime ts} \le M\,x_{njzi}^{\prime ts} \quad\forall n \in N,\quad\forall z \in Z,\quad\forall j \in J,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S $$

(18)

$$ y_{njpi}^{\prime\prime ts} \le M\,y_{njpi}^{\prime ts} \quad\forall n \in N,\quad\forall p \in P,\quad\forall j \in J,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S $$

(19)

$$ \sum\limits_{n \in N} {\sum\limits_{j \in J} {x_{njzi}^{\prime ts} } } \ge 1\quad\forall z \in Z,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S $$

(20)

$$ \sum\limits_{n \in N} {\sum\limits_{j \in J} {y_{njpi}^{\prime ts} } } \ge 1\quad\forall p \in P,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S $$

(21)

$$ \sum\limits_{n \in N} {\sum\limits_{i \in I} {x_{njzi}^{\prime \prime ts} } } \le C_{zj} \quad\forall z \in Z,\quad\forall j \in J,\quad\forall t \in T,\quad\forall s \in S $$

(22)

$$ I_{njz}^{ts} \le U_{z} \quad\forall j \in J,\quad\forall z \in Z,\quad\forall n \in N,\quad\forall t \in T,\quad\forall s \in S\, $$

(23)

$$ I_{njp}^{\prime ts} \le U_{p}^{\prime} \quad\forall j \in J,\quad\forall p \in P,\quad\forall n \in N,\quad\forall t \in T,\quad\forall s \in S\, $$

(24)

$$ \sum\limits_{n \in N} {\sum\limits_{i \in I} {y_{njpi}^{\prime \prime ts} } } \le C_{pj}^{\prime } \quad\forall p \in P,\quad\forall j \in J,\quad\forall t \in T,\quad\forall s \in S $$

(25)

$$ d_{ij} A_{jqi}^{\prime ts} \le r_{q} \quad\forall q \in Q,\quad\forall j \in J,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S $$

(26)

$$ A_{jqi}^{\prime ts} \le A_{j} \quad\forall q \in Q,\quad\forall j \in J,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S $$

(27)

$$ A_{jqi}^{\prime\prime ts} \le MA_{jqi}^{\prime ts} \quad\forall q \in Q,\quad\forall j \in J,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S $$

(28)

$$ \sum\limits_{j \in J} {A_{jqi}^{\prime ts} } \ge 1\quad\forall q \in Q,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S $$

(29)

$$ S_{jl}^{ts} \le \lambda_{jl} \sum\limits_{k \in K} {\sum\limits_{i \in I} {\eta_{jlik}^{ts} } } \quad\forall j \in J,\quad\forall l \in L,\quad\forall t \in T,\quad\forall s \in S $$

(30)

$$ \eta_{jlik}^{ts} d_{ij} \le S_{jl}^{ts} \quad\forall j \in J,\quad\forall l \in L,\quad\forall i \in I,\quad\forall k \in K,\quad\forall t \in T,\quad\forall s \in S $$

(31)

$$ \eta_{jlik}^{ts} \le A_{j} \quad\forall j \in J,\quad\forall l \in L,\quad\forall i \in I,\quad\forall k \in K,\quad\forall s \in T,\quad\forall s \in S $$

(32)

$$ d_{ij} \eta_{jlik}^{ts} \le T_{i}^{ts} V_{l} \quad\forall j \in J,\quad\forall l \in L,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S $$

(33)

$$ \sum\limits_{j \in J} {\sum\limits_{l \in L} {\sum\limits_{k \in K} {\eta_{jlik}^{ts} } } \ge 1\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S} $$

(34)

$$ \sum\limits_{j \in J} {\sum\limits_{k \in K} {\sum\limits_{l \in L} {\eta_{jlik}^{ts} g_{l} } } } + \delta_{i}^{\prime \prime ts} = D_{i}^{\prime \prime ts} \quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S $$

(35)

$$ \sum\limits_{j \in J} {I_{jq}^{\prime \prime \prime t - 1\,s} } - \,\sum\limits_{j \in J} {I_{jq}^{\prime \prime \prime ts} } + \delta_{jq}^{\prime \prime \prime ts} + \sum\limits_{j \in J} {\sum\limits_{i \in I} {A_{jqi}^{\prime \prime ts} } } = \sum\limits_{i \in I} {D_{iq}^{\prime \prime \prime ts} } \quad\forall q \in Q,\quad\forall t \in T,\quad\forall s \in S $$

(36)

$$ I_{jq}^{\prime \prime \prime ts} \le U_{q}^{\prime \prime \prime } \,\quad\forall q \in Q,\quad\forall j \in J,\quad\forall t \in T,\quad\forall s \in S\, $$

(37)

$$ ({\text{FC}}_{s} + {\text{VC}}_{s} + {\text{OC}}_{s} + {\text{TC}}_{s} + {\text{IC}}_{s} ) - \sum\limits_{{s^{\prime} \in S}} {p_{{s^{\prime}}} ({\text{FC}}_{{s^{\prime}}} + {\text{VC}}_{{s^{\prime}}} + {\text{OC}}_{{s^{\prime}}} + {\text{TC}}_{{s^{\prime}}} + {\text{IC}}_{{s^{\prime}}} )} + \theta_{s} \ge 0\quad\forall s \in S $$

(38)

$$ A_{j} \in \{ 0,1\} \quad\forall j \in J $$

(39)

$$ \eta_{jlik}^{ts} \in \{ 0,1\} \quad\forall l \in L,\quad\forall k \in K,\quad\forall j \in J,\quad\forall i \in I,\quad\forall j \in J,\quad\forall t \in T,\quad\forall s \in S $$

(40)

$$ A_{jqi}^{\prime ts} \in \{ 0,1\} \quad\forall j \in J,\quad\forall q \in Q,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S $$

(41)

$$ y_{njpi}^{\prime ts} \in \{ 0,1\} \quad\forall i \in I,\quad\forall n \in N,\quad\forall j \in J,\quad\forall p \in P,\quad\forall t \in T,\quad\forall s \in S $$

(42)

$$ y_{jq}^{\prime \prime ts} \in \{ 0,1\} \quad\forall j \in J,\quad\forall q \in Q,\,\quad\forall t \in T,\quad\forall s \in S $$

(43)

$$ y_{qk}^{\prime \prime \prime ts} \in \{ 0,1\} \quad\forall q \in Q,\quad\forall k \in K,\,\quad\forall t \in T,\quad\forall s \in S $$

(44)

$$ x_{nk}^{ts} \in \{ 0,1\} \quad\forall n \in N,\quad\forall k \in K,\,\quad\forall t \in T,\quad\forall s \in S $$

(45)

$$ x_{njzi}^{\prime ts} \in \{ 0,1\} \quad\forall z \in Z,\quad\forall i \in I,\quad\forall n \in N,\quad\forall j \in J,\,\quad\forall t \in T,\quad\forall s \in S $$

(46)

$$ Z_{nmk}^{ts} \in \{ 0,1\} \quad\forall k \in K,\quad\forall n \in N,\quad\forall m \in N,\,\quad\forall t \in T,\quad\forall s \in S $$

(47)

$$ S_{jl}^{ts} \ge 0\quad\forall j \in J,\quad\forall l \in L,\quad\forall t \in T,\quad\forall s \in S $$

(48)

$$ x_{njzi}^{\prime \prime ts} \ge 0\quad\forall n \in N,\quad\forall j \in J,\quad\forall i \in I,\,\quad\forall z \in Z,\quad\forall t \in T,\quad\forall s \in S $$

(49)

$$ y_{njpi}^{\prime \prime ts} \ge 0\quad\forall n \in N,\quad\forall j \in J,\quad\forall i \in I,\,\quad\forall p \in P,\quad\forall t \in T,\quad\forall s \in S $$

(50)

$$ I_{nkz}^{ts} \ge 0\quad\forall z \in Z,\quad\forall n \in N,\quad\forall k \in K,\,\quad\forall t \in T,\quad\forall s \in S $$

(51)

$$ I_{nkp}^{\prime ts} \ge 0\quad\forall p \in P,\quad\forall n \in N,\quad\forall k \in K,\,\quad\forall t \in T,\quad\forall s \in S $$

(52)

$$ I_{jq}^{\prime\prime\prime ts} \ge 0\quad\forall z \in Z,\quad\forall n \in N,\quad\forall k \in K,\,\quad\forall t \in T,\quad\forall s \in S $$

(53)

$$ A_{jqi}^{\prime\prime ts} \ge 0\quad\forall q \in Q,\quad\forall j \in J,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S $$

(54)

$$ \delta_{iz}^{ts} \ge 0\quad\forall i \in Z,\quad\forall z \in Z,\quad\forall t \in T,\quad\forall s \in S $$

(55)

$$ \delta_{ip}^{\prime ts} \ge 0\quad\forall i \in I,\quad\forall p \in P,\quad\forall t \in T,\quad\forall s \in S $$

(56)

$$ \delta_{i}^{\prime\prime ts} \ge 0\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S $$

(57)

$$ \delta_{iq}^{\prime ts} \ge 0\quad\forall i \in I,\quad\forall q \in Q,\quad\forall t \in T,\quad\forall s \in S. $$

(58)

Objective function Eq. (6) minimizes the total cost. The first part of Eq. (6) is the expected value of the total cost in the both stages. The second part of this equation is related to the total cost variability and the last term calculates the penalty of infeasibility. Equation (7) guarantees that utmost one emergency tent can be located in each node. Equation (8) shows that emergency tents cannot move from a location where no emergency tent has been located in the last period. Equation (9) clarifies the capacity of emergency tents for each relief base. Equations (10), (11), (26), and (31) enforce coverage radius restrictions. Equation (12) illustrates how an emergency tent can be located on or moved from a node. Equations (13), (14), (35), and (36) determine the inventory level of relief commodities and blood supplies and the under-fulfillment of relief commodity and blood demand. Equation (15) guarantees that emergency tents can only be assigned to open relief bases. Equations (16) and (17) ensure that relief commodities or blood supplies in emergency tents can be transported to affected areas if and only if they have been located. Equations (18) and (19) explain that the relief commodities and blood supplies given by a relief base cannot be transported from an emergency tent which is not assigned to that relief base. Equations (20), (21), and (34) assert that demand for each relief commodity, blood supply, and evacuation operation must be satisfied at least partially. Equations (22) and (25) determine available relief commodities and blood supplies at relief bases. Equation (23) and (24) limit the inventory level of relief commodities and blood supplies at emergency tents. Equation (27) explains that drugs can be distributed in affected areas if and only if those areas are assigned to open relief bases. Equation (28) clarifies that drugs given by a relief base cannot be transported to an affected area if it is not assigned to that relief base. Equation (29) ensures that demand for drugs should be satisfied at least partially. Equation (30) determines the radius coverage of each relief base during the evacuation operation. Equation (31) ensures that evacuations must be completed in specific time frames. Equation (32) shows evacuations can be started if the operation is assigned to an open relief base. Equation (37) expresses the capacity of drug storage at each relief base. Equation (38) acts as an auxiliary equation of the robust model which linearizes the proposed model. Equation (39) through Eq. (58) define binary and positive decision variables.

p-robust model

In the previous section, we presented a robust humanitarian logistics network which determines location and distribution decisions for the preparedness and response phases in disaster management. Now, we will complete this model to be more practical in a real-world situation. As stated in the previous section, many studies, such as Barzinpour and Esmaeili (2014b), assume that facility locations and pathways remain unaffected during a disaster; however, it is obvious that these sites may be located on fault lines. Consequently, these sites may be gravely affected during an earthquake. Therefore, we use the Monte Carlo simulation to generate scenarios to challenge possible disruption of pathways and damage to relief bases after an earthquake hits. After that, p-robust programming will be applied to formulate these possible occurrences.

We assume that two different events can occur after an earthquake: relief base and pathway disruption. Based on the Monte Carlo simulation and generating random data, we can determine different scenarios related to possible damages. The method of generating scenarios for affected sites is shown in Fig. 2. This flow chart generates different scenarios which are used in the p-robust model. For example, in a given scenario, it determines that the pathway between relief base 2 and affected area 3 will be disrupted. By considering all scenarios and all possible damages along pathways and among relief bases, we will have new problems which can be formulated by p-robust optimization.

Fig. 2

Monte Carlo simulation flow chart to generate disruption scenarios

To introduce the robust measure, we use in this section, let E be a set of scenarios which are derived by the Monte Carlo simulation. Let ($p_{e}^{\prime }$) be a deterministic (i.e., single-scenario) minimization problem, indexed by the scenario index e. (That is, for each scenario e ∈ E, there is a different problem ($p_{e}^{\prime }$)). The structure of these problems is identical; only the data are different. For each e, let ${\rm PR}_{e}^{*}$ be the optimal objective value for ($p_{e}^{\prime }$); we assume ${\rm PR}_{e}^{*}$ > 0 for all e. The notion of p-robustness was first introduced in the context of facility layout (Kouvelis, Kurawarwala, and Gutierrez 1992) and used subsequently in the context of an international sourcing problem (Gutierrez and Kouvelis 1995) and a network design problem (Gutiérrez 1996).

Let P ≥ 0 be a constant. Let X be a feasible solution to ($p_{e}^{\prime }$) for all e ∈ E, and let ${\rm PR}_{e}^{*}$ (X) be the objective value of problem ($p_{e}^{\prime }$) under solution x. x is called p-robust if for all e ∈ E,

$$ {\rm PR}_{e}^{*} \left( {\text{X}} \right) - {\rm PR}_{e}^{*} \le ( 1+ p^{\prime } ) {\rm PR}_{e}^{*} . $$

(59)

The left-hand side of the equation above is the relative regret for scenario e; the absolute regret is given by ${\rm PR}_{e}^{*} \left( {\text{X}} \right) - {\rm PR}_{e}^{*}$.

According to the given explanation, some variables must be changed as listed below:

$\eta_{jlik}^{tse}$ :

If rescue vehicle ℓ from relief base j is assigned to affected area i and hospital k in period t and under scenario s and scenario e equal to 1, otherwise 0

$A_{jqi}^{\prime tse}$ :

If relief base j is assigned to affected area i to cover demand of commodity q in period t under scenario s and scenario e equal to ℓ, otherwise 0

$A_{jqi}^{\prime\prime tse}$ :

Quantity of commodity q transported from relief base j to affected area i in period t under scenario s and scenario e

$S_{jl}^{tse}$ :

Coverage radius of rescue vehicle ℓ at relief base j in period t under scenario s and scenario e

$x_{nj}^{tse}$ :

If an emergency tent belongs to relief base j which is located at site n in period t under scenario s and scenario e equal to 1, otherwise 0

$Z_{nmj}^{tse}$ :

If an emergency tent from relief base j is located at location m in period t − 1 and moves to location n in period t under scenario s and scenario e equal to 1, otherwise 0

$x_{njzi}^{\prime tse}$ :

If an emergency from relief base j at point n is assigned to affected area i to cover demand of drug z in period t under scenario s and scenario e equal to 1, otherwise 0

$x_{njzi}^{\prime \prime tse}$ :

Quantity of transported drug z at emergency tent n from relief base j to affected area i in period t under scenario s and scenario e

$y_{njpi}^{\prime tse}$ :

If an emergency from relief base j at point n is assigned to affected area i to cover demand of blood supply p in period t under scenario s and scenario e equal to 1, otherwise 0

$y_{njpi}^{\prime \prime tse}$ :

Quantity of blood supply p transported from emergency tent n, belongs to relief base j, to affected area i in period t under scenario s and scenario e

$I_{njz}^{tse}$ :

Inventory level of drug z at emergency tent n which belongs to relief base j at the end of period t under scenario s and scenario e

$I_{njp}^{\prime tse}$ :

Inventory level of blood supply p at emergency tent n which belongs to relief base j at the end of period t under scenario s and scenario e

$I_{jq}^{\prime \prime \prime tse}$ :

Inventory level of commodity q at relief base j at the end of period t under scenario s and scenario e

$\delta_{iz}^{tse}$ :

Unsatisfied demand of drug z at affected area i in period t under scenario s and scenario e

$\delta_{ip}^{\prime tse}$ :

Unsatisfied demand of blood supply p at affected area i in period t under scenario s and scenario e

$\delta_{i}^{\prime \prime tse}$ :

Uncovered injured people at affected area i in period t under scenario s and scenario e

$\delta_{iq}^{\prime \prime \prime tse}$ :

Unsatisfied demand of commodity q at affected area i in period t under scenario s and scenario e

For each scenario (E) optimum value of objective function regard to model 2 must be calculated. Model 2 is described as follows:

Min

$$ \sum\limits_{s \in S} {p_{s} ({\text{FC}}_{se} + {\text{VC}}_{se} + {\text{OC}}_{se} + {\text{TC}}_{se} + {\text{IC}}_{se} )} + \lambda \,\sum\limits_{s \in S} {p_{s} [({\text{FC}}_{se} + {\text{VC}}_{se} + {\text{OC}}_{se} + {\text{TC}}_{se} + {\text{IC}}_{se} ) - \sum\limits_{{s^{\prime } \in S}} {p_{{s^{\prime}}} ({\text{FC}}_{{s^{\prime } e}} + {\text{VC}}_{{s^{\prime } e}} + {\text{OC}}_{{s^{\prime } e}} + {\text{TC}}_{{s^{\prime } e}} + {\text{IC}}_{{s^{\prime } e}} )} + 2\theta_{s} ]} + \omega \,\sum\limits_{I \in I} {\sum\limits_{z \in Z} {\sum\limits_{t \in T} {p_{s} \delta_{iz}^{tse} } } } + \omega^{\prime } \,\sum\limits_{I \in I} {\sum\limits_{z \in Z} {\sum\limits_{t \in T} {p_{s} \delta_{ip}^{\prime ts} } } } + \omega^{\prime \prime } \,\sum\limits_{I \in I} {\sum\limits_{z \in Z} {\sum\limits_{t \in T} {p_{s} \delta_{i}^{\prime \prime tse} } } } + \omega^{\prime \prime \prime } \,\sum\limits_{I \in I} {\sum\limits_{z \in Z} {\sum\limits_{t \in T} {p_{s} \delta_{iq}^{\prime \prime \prime tse} } } }. $$

(60)

Subject to:

$$ \sum\limits_{j \in J} {x_{nj}^{tse} } + \sum\limits_{j \in J} {\sum\limits_{m \in N} {Z_{nmj}^{tse} } } \le 1\quad\forall n \in N,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(61)

$$ \sum\limits_{j \in J} {\sum\limits_{m \in N} {Z_{mnj}^{tse} } } \le \sum\limits_{j \in J} {\sum\limits_{m \in N} {Z_{nmj}^{t - 1\,se} } } + \sum\limits_{j \in J} {x_{nj}^{t - 1se} } \quad\forall n \in N,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(62)

$$ \sum\limits_{t \in T} {\sum\limits_{n \in N} {x_{nj}^{tse} } \le m_{j} } \quad\forall j \in J,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(63)

$$ d_{in} x_{injzi}^{\prime tse} \le r\quad\forall z \in Z,\quad\forall j \in J,\quad\forall n \in N,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(64)

$$ d_{in} y_{injpi}^{\prime tse} \le r\quad\forall p \in P,\quad\forall j \in J,\quad\forall n \in N,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(65)

$$ 1 - \sum\limits_{j \in J} {x_{nj}^{tse} } - \sum\limits_{j \in J} {\sum\limits_{m \in N} {Z_{nmj}^{tse} } } \ge \sum\limits_{j \in J} {x_{nj}^{t + 1\,se} } + \sum\limits_{j \in J} {\sum\limits_{m \in N} {Z_{nmj}^{t + 1\,se} } } \quad\forall n \in N,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(66)

$$ \sum\limits_{n \in N} {\sum\limits_{j \in J} {I_{nkj}^{t - 1\,se} } } - \,\sum\limits_{n \in N} {\sum\limits_{j \in J} {I_{nkj}^{tse} } } + \delta_{iz}^{tse} + \sum\limits_{n \in N} {\sum\limits_{j \in J} {x_{njzi}^{\prime\prime tse} } } = D_{iz}^{ts} \quad\forall i \in I,\quad\forall z \in Z,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(67)

$$ \sum\limits_{n \in N} {\sum\limits_{j \in J} {I_{njp}^{\prime t - 1\,se} } } - \,\sum\limits_{n \in N} {\sum\limits_{j \in J} {I_{njp}^{\prime ts} } } + \delta_{ip}^{\prime tse} + \sum\limits_{n \in N} {\sum\limits_{j \in J} {y_{njpi}^{\prime\prime tse} } } = D_{ip}^{\prime ts} \quad\forall i \in I,\quad\forall p \in P,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(68)

$$ x_{nj}^{tse} \le MA_{j} \quad\forall n \in N,\quad\forall j \in J,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(69)

$$ x_{njzi}^{\prime tse} \le M\,\left(x_{nj}^{tse} + \sum\limits_{m \in N} {Z_{nmj}^{tse} } \right)\quad\forall n \in N,\quad\forall j \in J,\quad\forall i \in I,\quad\forall z \in Z,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(70)

$$ y_{njpi}^{\prime tse} \le M\,\left(x_{nj}^{tse} + \sum\limits_{m \in N} {Z_{nmj}^{tse} } \right)\quad\forall n \in N,\quad\forall j \in J,\quad\forall i \in I,\quad\forall p \in P,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(71)

$$ x_{njzi}^{\prime\prime tse} \le M\,x_{njzi}^{\prime tse} \quad\forall n \in N,\quad\forall z \in Z,\quad\forall j \in J,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S $$

(72)

$$ y_{njpi}^{\prime\prime tse} \le M\,y_{njpi}^{\prime tse} \quad\forall n \in N,\quad\forall p \in P,\quad\forall j \in J,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S $$

(73)

$$ \sum\limits_{n \in N} {\sum\limits_{j \in J} {x_{njzi}^{\prime tse} } } \ge 1\quad\forall z \in Z,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S $$

(74)

$$ \sum\limits_{n \in N} {\sum\limits_{j \in J} {y_{njpi}^{\prime tse} } } \ge 1\quad\forall p \in P,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(75)

$$ \sum\limits_{n \in N} {\sum\limits_{i \in I} {x_{njzi}^{\prime \prime tse} } } \le C_{zj} \quad\forall z \in Z,\quad\forall j \in J,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(76)

$$ I_{njz}^{tse} \le U_{z} \quad\forall j \in J,\quad\forall z \in Z,\quad\forall n \in N,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E\, $$

(77)

$$ I_{njp}^{\prime tse} \le U_{p}^{\prime} \quad\forall j \in J,\quad\forall p \in P,\quad\forall n \in N,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(78)

$$ \sum\limits_{n \in N} {\sum\limits_{i \in I} {y_{njpi}^{\prime \prime ts} } } \le C_{pj}^{\prime } \quad\forall p \in P,\quad\forall j \in J,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(79)

$$ d_{ij} A_{jqi}^{\prime tse} \le r_{q} \quad\forall q \in Q,\quad\forall j \in J,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(80)

$$ A_{jqi}^{\prime tse} \le A_{j} \quad\forall q \in Q,\quad\forall j \in J,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(81)

$$ A_{jqi}^{\prime\prime tse} \le MA_{jqi}^{\prime tse} \quad\forall q \in Q,\quad\forall j \in J,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(82)

$$ \sum\limits_{j \in J} {A_{jqi}^{\prime tse} } \ge 1\quad\forall q \in Q,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(83)

$$ S_{jl}^{tse} \le \lambda_{jl} \sum\limits_{k \in K} {\sum\limits_{i \in I} {\eta_{jlik}^{tse} } } \quad\forall j \in J,\quad\forall l \in L,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(84)

$$ \eta_{jlik}^{tse} d_{ij} \le S_{jl}^{tse} \quad\forall j \in J,\quad\forall l \in L,\quad\forall i \in I,\quad\forall k \in K,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(85)

$$ \eta_{jlik}^{tse} \le A_{j} \quad\forall j \in J,\quad\forall l \in L,\quad\forall i \in I,\quad\forall k \in K,\quad\forall s \in T,\quad\forall s \in S,\quad\forall e \in E $$

(86)

$$ d_{ij} \eta_{jlik}^{tse} \le T_{i}^{ts} V_{l} \quad\forall j \in J,\quad\forall l \in L,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(87)

$$ \sum\limits_{j \in J} {\sum\limits_{l \in L} {\sum\limits_{k \in K} {\eta_{jlik}^{tse} } } \ge 1\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S} ,\quad\forall e \in E $$

(88)

$$ \sum\limits_{j \in J} {\sum\limits_{k \in K} {\sum\limits_{l \in L} {\eta_{jlik}^{tse} g_{l} } } } + \delta_{i}^{\prime \prime tse} = D_{i}^{\prime \prime ts} \quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(89)

$$ \sum\limits_{j \in J} {I_{jq}^{\prime \prime \prime t - 1\,se} } - \,\sum\limits_{j \in J} {I_{jq}^{\prime \prime \prime tse} } + \delta_{jq}^{\prime \prime \prime tse} + \sum\limits_{j \in J} {\sum\limits_{i \in I} {A_{jqi}^{\prime \prime tse} } } = \sum\limits_{i \in I} {D_{iq}^{\prime \prime \prime ts} } \quad\forall q \in Q,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(90)

$$ I_{jq}^{\prime \prime \prime tse} \le U_{q}^{\prime \prime \prime } \,\quad\forall q \in Q,\quad\forall j \in J,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(91)

$$ ({\text{FC}}_{se} + {\text{VC}}_{se} + {\text{OC}}_{se} + {\text{TC}}_{se} + {\text{IC}}_{se} ) - \sum\limits_{{s^{\prime} \in S}} {p_{{s^{\prime}}} ({\text{FC}}_{{s^{\prime}e}} + {\text{VC}}_{{s^{\prime}e}} + {\text{OC}}_{{s^{\prime}e}} + {\text{TC}}_{{s^{\prime}e}} + {\text{IC}}_{{s^{\prime}e}} )} + \theta_{s} \ge 0 \quad \forall s \in S,\quad\forall e \in E $$

(92)

$$ A_{j} \in \{ 0,1\} \quad\forall j \in J $$

(93)

$$ \eta_{jlik}^{tse} \in \{ 0,1\} \quad\forall l \in L,\quad\forall k \in K,\quad\forall j \in J,\quad\forall i \in I,\quad\forall j \in J,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(94)

$$ A_{jqi}^{\prime tse} \in \{ 0,1\} \quad\forall j \in J,\quad\forall q \in Q,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(95)

$$ y_{njpi}^{\prime tse} \in \{ 0,1\} \quad\forall i \in I,\quad\forall n \in N,\quad\forall j \in J,\quad\forall p \in P,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(96)

$$ y_{jq}^{\prime \prime tse} \in \{ 0,1\} \quad\forall j \in J,\quad\forall q \in Q,\,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(97)

$$ y_{qk}^{\prime \prime \prime tse} \in \{ 0,1\} \quad\forall q \in Q,\quad\forall k \in K,\,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(98)

$$ x_{nk}^{tse} \in \{ 0,1\} \quad\forall n \in N,\quad\forall k \in K,\,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(99)

$$ x_{njzi}^{\prime tse} \in \{ 0,1\} \quad\forall z \in Z,\quad\forall i \in I,\quad\forall n \in N,\quad\forall j \in J,\,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(100)

$$ Z_{nmk}^{tse} \in \{ 0,1\} \quad\forall k \in K,\quad\forall n \in N,\quad\forall m \in N,\,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(101)

$$ S_{jl}^{tse} \ge 0\quad\forall j \in J,\quad\forall l \in L,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(102)

$$ x_{njzi}^{\prime\prime tse} \ge 0\quad\forall n \in N,\quad\forall j \in J,\quad\forall i \in I,\,\quad\forall z \in Z,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(103)

$$ y_{njpi}^{\prime\prime tse} \ge 0\quad\forall n \in N,\quad\forall j \in J,\quad\forall i \in I,\,\quad\forall p \in P,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(104)

$$ I_{nkz}^{tse} \ge 0\quad\forall z \in Z,\quad\forall n \in N,\quad\forall k \in K,\,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(105)

$$ I_{nkp}^{\prime tse} \ge 0\quad\forall p \in P,\quad\forall n \in N,\quad\forall k \in K,\,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(106)

$$ I_{jq}^{\prime\prime\prime tse} \ge 0\quad\forall z \in Z,\quad\forall n \in N,\quad\forall k \in K,\,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(107)

$$ A_{jqi}^{\prime\prime tse} \ge 0\quad\forall q \in Q,\quad\forall j \in J,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(108)

$$ \delta_{iz}^{tse} \ge 0\quad\forall i \in Z,\quad\forall z \in Z,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(109)

$$ \delta_{ip}^{\prime tse} \ge 0\quad\forall i \in I,\quad\forall p \in P,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(110)

$$ \delta_{i}^{\prime\prime tse} \ge 0\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(111)

$$ \delta_{iq}^{\prime tse} \ge 0\quad\forall i \in I,\quad\forall q \in Q,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E. $$

(112)

Equation (60) through Eq. (112) do the same as Eq. (6) through Eq. (58).

Model 2 is solved for each scenario, and the optimum value of our objective function which is named ${\rm PR}_{e}^{*}$ will be calculated. According to the p-robust method, the effect of each scenario must be involved in the optimum structure of the humanitarian logistics network. Therefore, Model 3 is used to build the network.

Min

$$ \sum\limits_{s \in S} {p_{s} ({\text{FC}}_{s0} + {\text{VC}}_{s0} + {\text{OC}}_{s0} + {\text{TC}}_{s0} + {\text{IC}}_{s0} )} + \lambda \,\sum\limits_{s \in S} {p_{s} [({\text{FC}}_{s0} + {\text{VC}}_{s0} + {\text{OC}}_{s0} + {\text{TC}}_{s0} + {\text{IC}}_{s0} ) - \sum\limits_{{s^{\prime } \in S}} {p_{{s^{\prime}}} ({\text{FC}}_{{s^{\prime } 0}} + {\text{VC}}_{{s^{\prime } 0}} + {\text{OC}}_{{s^{\prime } 0}} + {\text{TC}}_{{s^{\prime } 0}} + {\text{IC}}_{{s^{\prime } 0}} )} + 2\theta_{s} ]} + \omega \,\sum\limits_{I \in I} {\sum\limits_{z \in Z} {\sum\limits_{t \in T} {p_{s} \delta_{iz}^{ts0} } } } + \omega^{\prime } \,\sum\limits_{I \in I} {\sum\limits_{z \in Z} {\sum\limits_{t \in T} {p_{s} \delta_{ip}^{\prime ts0} } } } + \omega^{\prime \prime } \,\sum\limits_{I \in I} {\sum\limits_{z \in Z} {\sum\limits_{t \in T} {p_{s} \delta_{i}^{\prime \prime ts0} } } } + \omega^{\prime \prime \prime } \,\sum\limits_{I \in I} {\sum\limits_{z \in Z} {\sum\limits_{t \in T} {p_{s} \delta_{iq}^{\prime \prime \prime ts0} } } }. $$

(113)

Subject to:

$$ \sum\limits_{j \in J} {x_{nj}^{tse} } + \sum\limits_{j \in J} {\sum\limits_{m \in N} {Z_{nmj}^{tse} } } \le 1\quad\forall n \in N,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(114)

$$ \sum\limits_{j \in J} {\sum\limits_{m \in N} {Z_{mnj}^{tse} } } \le \sum\limits_{j \in J} {\sum\limits_{m \in N} {Z_{nmj}^{t - 1\,se} } } + \sum\limits_{j \in J} {x_{nj}^{t - 1se} } \quad\forall n \in N,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(115)

$$ \sum\limits_{t \in T} {\sum\limits_{n \in N} {x_{nj}^{tse} } \le m_{j} } \quad\forall j \in J,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(116)

$$ d_{in} x_{injzi}^{\prime tse} \le r\quad\forall z \in Z,\quad\forall j \in J,\quad\forall n \in N,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(117)

$$ d_{in} y_{injpi}^{\prime tse} \le r\quad\forall p \in P,\quad\forall j \in J,\quad\forall n \in N,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(118)

$$ 1 - \sum\limits_{j \in J} {x_{nj}^{tse} } - \sum\limits_{j \in J} {\sum\limits_{m \in N} {Z_{nmj}^{tse} } } \ge \sum\limits_{j \in J} {x_{nj}^{t + 1\,se} } + \sum\limits_{j \in J} {\sum\limits_{m \in N} {Z_{nmj}^{t + 1\,se} } } \quad\forall n \in N,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(119)

$$ \sum\limits_{n \in N} {\sum\limits_{j \in J} {I_{nkj}^{t - 1\,se} } } - \,\sum\limits_{n \in N} {\sum\limits_{j \in J} {I_{nkj}^{tse} } } + \delta_{iz}^{tse} + \sum\limits_{n \in N} {\sum\limits_{j \in J} {x_{njzi}^{\prime\prime tse} } } = D_{iz}^{ts} \quad\forall i \in I,\quad\forall z \in Z,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(120)

$$ \sum\limits_{n \in N} {\sum\limits_{j \in J} {I_{njp}^{\prime t - 1\,se} } } - \,\sum\limits_{n \in N} {\sum\limits_{j \in J} {I_{njp}^{\prime ts} } } + \delta_{ip}^{\prime tse} + \sum\limits_{n \in N} {\sum\limits_{j \in J} {y_{njpi}^{\prime\prime tse} } } = D_{ip}^{\prime ts} \quad\forall i \in I,\quad\forall p \in P,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(121)

$$ x_{nj}^{tse} \le MA_{j} \quad\forall n \in N,\quad\forall j \in J,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(122)

$$ x_{njzi}^{\prime tse} \le M\,\left(x_{nj}^{tse} + \sum\limits_{m \in N} {Z_{nmj}^{tse} } \right)\quad\forall n \in N,\quad\forall j \in J,\quad\forall i \in I,\quad\forall z \in Z,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(123)

$$ y_{njpi}^{\prime tse} \le M\,\left(x_{nj}^{tse} + \sum\limits_{m \in N} {Z_{nmj}^{tse} } \right)\quad\forall n \in N,\quad\forall j \in J,\quad\forall i \in I,\quad\forall p \in P,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(124)

$$ x_{njzi}^{\prime\prime tse} \le M\,x_{njzi}^{\prime tse} \quad\forall n \in N,\quad\forall z \in Z,\quad\forall j \in J,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S $$

(125)

$$ y_{njpi}^{\prime\prime tse} \le M\,y_{njpi}^{\prime tse} \quad\forall n \in N,\quad\forall p \in P,\quad\forall j \in J,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S $$

(126)

$$ \sum\limits_{n \in N} {\sum\limits_{j \in J} {x_{njzi}^{\prime tse} } } \ge 1\quad\forall z \in Z,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S $$

(127)

$$ \sum\limits_{n \in N} {\sum\limits_{j \in J} {y_{njpi}^{\prime tse} } } \ge 1\quad\forall p \in P,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(128)

$$ \sum\limits_{n \in N} {\sum\limits_{i \in I} {x_{njzi}^{\prime \prime tse} } } \le C_{zj} \quad\forall z \in Z,\quad\forall j \in J,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(129)

$$ I_{njz}^{tse} \le U_{z} \quad\forall j \in J,\quad\forall z \in Z,\quad\forall n \in N,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E\, $$

(130)

$$ I_{njp}^{\prime tse} \le U_{p}^{\prime} \quad\forall j \in J,\quad\forall p \in P,\quad\forall n \in N,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(131)

$$ \sum\limits_{n \in N} {\sum\limits_{i \in I} {y_{njpi}^{\prime \prime ts} } } \le C_{pj}^{\prime } \quad\forall p \in P,\quad\forall j \in J,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(132)

$$ d_{ij} A_{jqi}^{\prime tse} \le r_{q} \quad\forall q \in Q,\quad\forall j \in J,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(133)

$$ A_{jqi}^{\prime tse} \le A_{j} \quad\forall q \in Q,\quad\forall j \in J,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(134)

$$ A_{jqi}^{\prime\prime tse} \le MA_{jqi}^{\prime tse} \quad\forall q \in Q,\quad\forall j \in J,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(135)

$$ \sum\limits_{j \in J} {A_{jqi}^{\prime tse} } \ge 1\quad\forall q \in Q,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(136)

$$ S_{jl}^{tse} \le \lambda_{jl} \sum\limits_{k \in K} {\sum\limits_{i \in I} {\eta_{jlik}^{tse} } } \quad\forall j \in J,\quad\forall l \in L,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(137)

$$ \eta_{jlik}^{tse} d_{ij} \le S_{jl}^{tse} \quad\forall j \in J,\quad\forall l \in L,\quad\forall i \in I,\quad\forall k \in K,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(138)

$$ \eta_{jlik}^{tse} \le A_{j} \quad\forall j \in J,\quad\forall l \in L,\quad\forall i \in I,\quad\forall k \in K,\quad\forall s \in T,\quad\forall s \in S,\quad\forall e \in E $$

(139)

$$ d_{ij} \eta_{jlik}^{tse} \le T_{i}^{ts} V_{l} \quad\forall j \in J,\quad\forall l \in L,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(140)

$$ \sum\limits_{j \in J} {\sum\limits_{l \in L} {\sum\limits_{k \in K} {\eta_{jlik}^{tse} } } \ge 1\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S} ,\quad\forall e \in E $$

(141)

$$ \sum\limits_{j \in J} {\sum\limits_{k \in K} {\sum\limits_{l \in L} {\eta_{jlik}^{tse} g_{l} } } } + \delta_{i}^{\prime \prime tse} = D_{i}^{\prime \prime ts} \quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(142)

$$ \sum\limits_{j \in J} {I_{jq}^{\prime \prime \prime t - 1\,se} } - \,\sum\limits_{j \in J} {I_{jq}^{\prime \prime \prime tse} } + \delta_{jq}^{\prime \prime \prime tse} + \sum\limits_{j \in J} {\sum\limits_{i \in I} {A_{jqi}^{\prime \prime tse} } } = \sum\limits_{i \in I} {D_{iq}^{\prime \prime \prime ts} } \quad\forall q \in Q,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(143)

$$ I_{jq}^{\prime \prime \prime tse} \le U_{q}^{\prime \prime \prime } \,\quad\forall q \in Q,\quad\forall j \in J,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(144)

$$ ({\text{FC}}_{se} + {\text{VC}}_{se} + {\text{OC}}_{se} + {\text{TC}}_{se} + {\text{IC}}_{se} ) - \sum\limits_{{s^{\prime } \in S}} {p_{{s^{\prime } }} ({\text{FC}}_{{s^{\prime } e}} + {\text{VC}}_{{s^{\prime}e}} + {\text{OC}}_{{s^{\prime } e}} + {\text{TC}}_{{s^{\prime } e}} + {\text{IC}}_{{s^{\prime } e}} )} + \theta_{s} \ge 0 \quad \forall s \in S,\quad\forall e \in E. $$

(145)

$$ \sum\limits_{s \in S} {p_{s} ({\text{FC}}_{se} + {\text{VC}}_{se} + {\text{OC}}_{se} + {\text{TC}}_{se} + {\text{IC}}_{se} )} + \lambda \,\sum\limits_{s \in S} {p_{s} [({\text{FC}}_{se} + {\text{VC}}_{se} + {\text{OC}}_{se} + {\text{TC}}_{se} + {\text{IC}}_{se} ) - \sum\limits_{{s^{\prime } \in S}} {p_{{s^{\prime } }} ({\text{FC}}_{{s^{\prime } e}} + {\text{VC}}_{{s^{\prime } e}} + {\text{OC}}_{{s^{\prime } e}} + {\text{TC}}_{{s^{\prime } e}} + {\text{IC}}_{{s^{\prime } e}} )} + 2\theta_{se} ]} + \omega \,\sum\limits_{k} {\sum\limits_{p} {\sum\limits_{t} {p_{s} \delta_{kp}^{tse} } } } \le (1 + p^{\prime } ){\rm PR}_{e}^{*} \quad\forall e \in E/\{ 0\} $$

(146)

$$ A_{j} \in \{ 0,1\} \quad\forall j \in J $$

(147)

$$ \eta_{jlik}^{tse} \in \{ 0,1\} \quad\forall l \in L,\quad\forall k \in K,\quad\forall j \in J,\quad\forall i \in I,\quad\forall j \in J,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(148)

$$ A_{jqi}^{\prime tse} \in \{ 0,1\} \quad\forall j \in J,\quad\forall q \in Q,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(149)

$$ y_{njpi}^{\prime tse} \in \{ 0,1\} \quad\forall i \in I,\quad\forall n \in N,\quad\forall j \in J,\quad\forall p \in P,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(150)

$$ y_{jq}^{\prime \prime tse} \in \{ 0,1\} \quad\forall j \in J,\quad\forall q \in Q,\,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(151)

$$ y_{qk}^{\prime \prime \prime tse} \in \{ 0,1\} \quad\forall q \in Q,\quad\forall k \in K,\,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(152)

$$ x_{nk}^{tse} \in \{ 0,1\} \quad\forall n \in N,\quad\forall k \in K,\,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(153)

$$ x_{njzi}^{\prime tse} \in \{ 0,1\} \quad\forall z \in Z,\quad\forall i \in I,\quad\forall n \in N,\quad\forall j \in J,\,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(154)

$$ Z_{nmk}^{tse} \in \{ 0,1\} \quad\forall k \in K,\quad\forall n \in N,\quad\forall m \in N,\,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(155)

$$ S_{jl}^{tse} \ge 0\quad\forall j \in J,\quad\forall l \in L,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(156)

$$ x_{njzi}^{\prime \prime tse} \ge 0\quad\forall n \in N,\quad\forall j \in J,\quad\forall i \in I,\,\quad\forall z \in Z,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(157)

$$ y_{njpi}^{\prime \prime tse} \ge 0\quad\forall n \in N,\quad\forall j \in J,\quad\forall i \in I,\,\quad\forall p \in P,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(158)

$$ I_{nkz}^{tse} \ge 0\quad\forall z \in Z,\quad\forall n \in N,\quad\forall k \in K,\,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(159)

$$ I_{nkp}^{\prime tse} \ge 0\quad\forall p \in P,\quad\forall n \in N,\quad\forall k \in K,\,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(160)

$$ I_{jq}^{\prime \prime \prime tse} \ge 0\quad\forall z \in Z,\quad\forall n \in N,\quad\forall k \in K,\,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(161)

$$ A_{jqi}^{\prime \prime tse} \ge 0\quad\forall q \in Q,\quad\forall j \in J,\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(162)

$$ \delta_{iz}^{tse} \ge 0\quad\forall i \in Z,\quad\forall z \in Z,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(163)

$$ \delta_{ip}^{\prime tse} \ge 0\quad\forall i \in I,\quad\forall p \in P,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(164)

$$ \delta_{i}^{\prime \prime tse} \ge 0\quad\forall i \in I,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E $$

(165)

$$ \delta_{iq}^{\prime tse} \ge 0\quad\forall i \in I,\quad\forall q \in Q,\quad\forall t \in T,\quad\forall s \in S,\quad\forall e \in E. $$

(166)

Equation (149) explains the p-robust criterion, so that for each scenario, the cost may not be more than $100\,\% \,(1 + p^{\prime } )$ of its optimal cost that is ${\rm PR}_{e}^{*}$ (value of $p^{\prime }$ is relative to the necessity of its scenario). Other equations are the same as the aforementioned equations in the robust model.

Computational result and discussion

The Bam earthquake on December 26, 2003, The Manjil–Rudbar earthquake on June 20, 1990 and other examples show that earthquakes have always been known to be the most devastating disasters in Iran among other natural disasters. This is true because of the geographical location of Iran, and because 90 percent of Iran is located on faults. For example, Tehran, as a strategic city in Iran, has always been exposed to such disasters. Regarding earthquakes, Tehran is considered a dangerous region (8–10 Mercalli scales). The fault in the northern region of Tehran is the biggest fault line of the city. It is located in the south foothills of the Alborz Range and to the north of Tehran. This fault starts in Lashkarak and Sohanak, continues in Farahzad and Hesarak, and continues towards the west. This fault encompasses Niavaran, Tajrish, Zaferanieh, Elahieh, and Farmanieh along its path. The necessity of attending to crisis management is clearly an issue with regard to the dangerous and risky situations in Tehran (Sabzehchian et al. 2006). According to Nateghi-A (2001), a 0.35 g scenario in Tehran would collapse about 640,000 domiciles out of 1,100,000, and about 1,450,000 people would be killed, and about 4,330,000 would suffer injuries.

Case description

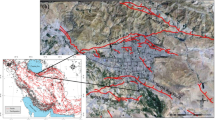
In this section, we propose a case study in a district of Tehran to show the effectiveness of our robust and p-robust models. Figure 3 demonstrates district 1 in Tehran, and it also shows locations of hospitals and potential locations of relief bases in this district.

Fig. 3

Located hospitals and potential locations of relief bases

According to this case study, we consider two periods, three hospitals, ten potential relief bases, and ten demand points that are widespread over this district. To cope with possible earthquakes, three types of relief commodities (water, food, and shelter) are considered in this case study. In addition, we consider just one blood supply and two types of drugs both of which are painkillers.

Based on the advice of disaster planners and historical records, we considered five scenarios, S ₁, S ₂, S ₃, S ₄, and S ₅. Demands for products and services under the 4th and 5th scenarios are more than other scenarios because of higher earthquake magnitude in these scenarios. To shed light on this, if the first scenario occurs, the first area demand for water will be around 4000 U. If the fifth scenario occurs, the first area demand for water will be around 19,000 U.

Table 1 shows the capacities of relief commodities, blood supply, drugs, and emergency tents for each potential relief base. The fixed cost of each potential relief base and its capacity for rescue vehicles are seen in Table 2. Table 3 consists of information pertaining to each type of rescue vehicles. We assume that the operational costs of rescue vehicles are $100, $200, and $1000. Each package of relief bases, such as water, food, and shelter, consists of 1000, 1000, and 1 units, respectively. Also the amounts of drugs type 1 and type 2 in each package are 1000 units.

Table 1 Capacities of relief commodities, blood supply, drugs, and emergency tents for each potential relief base

Table 2 Fixed cost of each potential relief base and its capacity for rescue vehicles

Table 3 Rescue vehicles information

During both periods, the moving cost is about $100, and according to Bozorgi-Amiri et al. (2013) and Jabbarzadeh et al. (2014), Table 4 shows units of transportation and operational costs for relief commodities, drugs, and blood supplies. We considered $200 for fixing emergency tents at each point. In addition, the capacities of emergency tents for relief drugs and blood are 4 and 7, respectively. The radius coverage of the emergency tents is 0.5 km and the radius coverage of relief commodities in relief bases is about 4 km. The demands for relief commodities, drugs, blood, and rescue vehicles for each period are shown in Table 5. In addition, Table 6 contains admissible time frames for evacuation operations under each scenario. The two following factors impact on demands and admissible time frames for each affected area under each scenario: (1) earthquake intensity and (2) population of the affected area.

Table 4 Unit of transportation, operation, and inventory cost for relief commodities, blood, and drugs

Table 5 Demands of affected area under each scenario

Table 6 Admissible time for evacuating operation under each scenario

The distance between two points can be calculated by the following Eq. (170). The latitude and longitude of affected areas, hospitals, and potential relief bases have been shown in Table 7. In addition, Table 8 shows the maximum capacity of each emergency tent for blood and drugs.

$$ d_{ij} = 6371.1 \times \arccos [\sin (LAT_{i} ) \times \sin (LAT_{j} ) + \cos (LAT_{i} ) \times \cos (LAT_{j} ) \times \cos (LONG_{j} - LONG_{i} )]. $$

(167)

Table 7 Latitude and longitude of affected areas, hospitals, and potential relief bases

Table 8 Capacity of each emergency tent for blood and drugs

Results

The proposed model was coded in GAMS on a laptop with Intel Core i2, 2.8 GHz, and 4 GB of RAM. Figure 4 summarizes our numerical example results at a penalty of $2500 for unsatisfied demand of relief commodities, $15,000 for blood, $2000 for drugs, and $3000 for the evacuation operation. The location of selected relief bases is shown in Fig. 4. According to Fig. 4, selected relief bases are 2, 4, and 5. Optimal decision variables are provided in Tables 9, 10, 11, and 12 under each scenario in each period. Table 9 shows located emergency tents of each relief base under each scenario in both periods. Because of decreasing demands in the second period, no new emergency tents will be placed in the second period and the proposed model illustrates that some of the emergency tents from the first period will be moved to new locations during the second period. Table 10 shows allocated demand points to emergency tents under each scenario in the first period. This table also demonstrates that more than one emergency may be satisfied at one demand point. In addition, Table 11 demonstrates allocated relief bases to each affected area to satisfy demand of relief commodities, such as water, food, and shelter under each scenario and in each period. Table 11 explains that one affected area may be satisfied by more than one relief base. According to our results, shortages happen under scenario 5 for water and shelter. Table 11 shows these shortages in a different color. We should say again that because of decreases in demands in the second period, less shortages will occur.

Fig. 4

Selected relief bases

Table 9 Located emergency tents of each relief base under each scenario in both periods

Table 10 Allocated demand points to emergency tents n from relief base j (n, j) under each scenario in the first period

Table 11 Allocated relief bases to each affected area to satisfy demand of relief commodities, such as water, food, and shelter under each scenario

Table 12 Impact of relief bases capacity of relief commodities on objective function of the robust model

To put all of this into perspective, virtually 140 thousand packages of water are distributed along with 90 thousand packages of food and about 100 packages of shelter. The total cost of the first and second stages of the proposed model for this solution is 3.678 million dollars.

To explore the effects of various problem parameters, the example problem is accompanied by sensitivity analysis experiments and corresponding managerial insights that can guide DMs under a variety of conditions.

Figure 5 and Table 12 represent the sensitivity analysis of relief bases’ capacities for relief commodities, such as water, food, and shelter. For capacity values equal or lower than 10 for each relief commodity, the solution will be infeasible. By increasing the capacity of relief bases for each relief commodity at the beginning, the objective function starts decreasing exponentially because of decreases in unsatisfied demand. However, after this turning point, the objective function starts growing because of increases in operational and inventory costs.

Fig. 5

Impact of relief bases capacity of relief commodities on objective function of the robust model

Increases in relief bases’ capacity are more than a special quantity for each commodity that does not create change in the robust model’s objective function. For example, relief bases’ capacity of shelters with more than 240 packages does not improve the objective function. In fact, relief bases with a capacity of more than 240 shelters apply as big M, since this parameter is located in right-hand side of constraints.

The based proposed flowchart in Fig. 2 and the Monte Carlo simulation relief bases and pathways may be down during an earthquake. In the first scenario, two pathways will be disrupted, but all of located relief bases survive during disaster. In the second scenario, located relief base 2 and three pathways will be disrupted. In the third scenario, located relief base 4 will be disrupted. Finally, in the last scenario, four pathways and located relief base 5 will be disrupted. The values of the objective functions for four scenarios are seen in Table 13. As it stated before, these values go into the p-robust model as ${\rm PR}_{e}^{*}$ parameters. According to the following table and our data in above tables, the p-robust model’s objective function is $3,912,000.

Table 13 Values of objective functions of the second model for four scenarios

To evaluate both the p-robust and robust models, two performance measures are used: the mean and standard deviation of objective function under random realizations. In addition, we vary the p-robust parameter between [0 1] and calculate the mean and standard deviation for p-robust and robust models. The results show that p-robust model gained the solutions with both higher quality and lower standard deviation than the robust model for fixed, moving, operational, transportation, and inventory costs.

Actually, in all problems, the p-robust approach dominates the robust model with respect to the mean of cost objective function value and its standard deviation. These results are seen in Table 14. The results imply that the p-robust strategy has a better performance in low values for p-robust parameters. As shown in Table 14, when the p-robust parameter increases, the mean of the objective function of the p-robust model is closer to the objective in the robust model. In addition, we should mention that because of the simulation’s nature in three cases, the robust objective function is better than the p-robust objective function. These cases are shown by a different color. Briefly, this table shows that the p-robust model decreases standard deviation in comparison with the robust model; similarly, it decreases the objective function of the proposed model. This is because the p-robust model considers each scenario with its possibility.

Table 14 Summary of test results of second objective function value and its standard deviation of both models

To determine the sensitivity of the p-robust model’s objective function value to variations in the p-robust parameter, a sensitivity analysis experiment is performed. Figure 6 shows sensitivity of the proposed model’s objective functions to variations in the p-robust parameter. Based on the proposed model with increases in the p-robust parameter, feasible region does not decrease. Therefore, we accept the increases of the mentioned parameter as it does not worsen our objective function.

Fig. 6

Sensitivity of the proposed model to variations in robust parameter

Conclusion and future research

Humanitarian logistics during disasters requires the consideration of numerous factors of which many are associated with a high range of uncertainty. Decision-making with uncertainties is a situation in which all disaster managers are met. Often, these decisions must be completed in the shortest possible time frames to ensure minimum casualties and financial losses. In this study, we used robust optimization approaches in resource allocation which can be a useful planning tool with the ability to deal with uncertainties in the environment.

In this paper, we proposed a dynamic robust model to optimize the humanitarian logistics network in the preparedness and response phases. Due to unforeseen events in the real world, scenario-based models are an intriguing subject for global and local organizations. Scenario-based models provide useful insight about a disaster aftermath and consider proper response requirements for urban areas. Our model contains two stages: the first stage determines the location and the number of relief bases, and the second stage determines the amount of transportation among relief bases to emergency tents, affected areas, and hospitals. The proposed model minimizes expected total costs, cost variability, and expected penalty for infeasible solutions due to uncertain parameters. In addition, we presented a p-robust model to consider possible disruptions by the disaster among located relief bases and pathways using the Monte Carlo simulation and the p-robust approach. Our results show that the proposed model assists DMs and organizations to improve both humanitarian and financial goals in the real world.

In conclusion, because like other studies, our paper is not without any deficiency, we offer the following suggestions for future researches: (1) consider more than one objective function, such as maximizing availability, reliability, and coverage; (2) propose new solution technique which can be one of the research areas in the future to manage humanitarian logistics network during the disaster; (3) use multi-level programing to bring up foreign organizations’ help as followers; and finally, (4) consider political constraints during the disaster if victims decline their right to assistance.