An EMQ inventory model for defective products involving rework and sales team’s initiatives-dependent demand

Abstract

This paper investigates the issue of an economic manufacturing quantity model for defective products involving imperfect production processes and rework. We consider that the demand is sensitive to promotional efforts/sales teams’ initiatives as well as the setup cost can be reduced through further investment. It also assumes that fixed quantity multiple installments of the finished batch are delivered to customers at a fixed interval of time. The long-run average cost function is derived and its convexity is proved via differential calculus. An effective iterative solution procedure is developed to achieve optimal replenishment lot-size, setup cost and the initiatives of sales teams so that the total cost of system is minimized. Numerical and sensitivity analyses are performed to evaluate the outcome of the proposed solution procedure presented in this research.

Introduction

In 1913, Harris (1990) first proposed the economic order quantity (EOQ) model to help companies in minimizing total inventory costs. The EOQ model utilizes mathematical techniques to symmetrize the setup and inventory holding costs as well as derives an optimal order size that minimizes the long-run average inventory costs. In the manufacturing sector, when parts are produced in-house instead of being purchased from outside suppliers, the economic manufacturing quantity model is often employed to cope with the finite inventory replenishment rate to minimize the expected overall cost per unit time (Hillier and Lieberman 2001). Despite the simplicity of EOQ and EMQ models they have been used broadly and are still applied industry-wide today; and many production-inventory models with more complicated and/or practical features were addressed extensively during the past decades (see Dutta et al. 2007, Taleizadeh et al. 2010a, b, 2013a, b; Crdenas-Barrn et al. 2012). Sarkar et al. (2014) recently developed an EMQ model with price- and time-dependent demand under the effect of reliability and inflation.

The traditional EOQ and EMQ inventory models assumed that all products are perfect. It is common in all industries that a certain percent of produced/ordered products are of imperfect quality. Moreover, imperfect quality products can be reworked and repaired in some circumstances. In view of this numerous studies have been carried out to enhance the EMQ model by addressing the issue of imperfect quality products produced and reworked (see So and Tang 1995; Shekarian et al. 2014; Taleizadeh et al. 2010c, 2011, 2013c; Pal et al. 2013; Hayek and Salameh 2001; Haji et al. 2008; Hafshejani et al. 2012; Chen 2013; Sarkar et al. 2014; Vishkaei et al. 2014). For instance, the plastic goods in plastic injection molding process, the printed circuit board assembly (PCBA) in PCBA manufacturing, etc. Therefore, overall production-inventory costs can be significantly reduced. Examples of articles that studied the effect of rework on optimal replenishment decisions are as follows. So and Tang (1995) studied an optimal operating policy for a production system with bottleneck and a random rework. Hayek and Salameh (2001) assumed that all defective items produced are repairable and derived an optimal operating policy for the EMQ model under the effect of reworking all defective items. Haji et al. (2008) addressed the rework of defective products in a multi-product single machine system. They adopted the common cycle time approach for all products, allowed non-zero set up times for normal production and rework process for each product. Then Sarkar et al. (2014) developed an economic production quantity model for defective products with backorders and rework process in a single stage production system.

In the highly competitive marketing environment, the managers of business organizations have a lot of pressure to sell products to downstream channel members. In general, vendors influence their customers with sales teams’ initiatives or promotional policies, i.e., free gifts, discounts, delay in payments, packaging, special services and advertising, among others (Crdenas-Barrn et al. 2014). Nair and Tarasewich (2003) have obtained the optimal design of promotional efforts such as free gifts, discounts and special services. Krishnan et al. (2004) have shown that pricing, displays, free goods and advertising are necessary actions to accomplish maximum revenues. Szmerekovsky and Zhang (2009) have addressed the pricing options and two-tier advertising actions between one manufacturer and one retailer when customers’ demand is dependent on the retail price and advertising by both players. Ramanathan and Muyldermans (2010) have studied the effect of promotional efforts on the sales of soft drinks. Sana (2010) has presented a multi-item EOQ model for perishable and ameliorating products when the time-varying demand is dependent on the enterprise’s initiatives such as advertising and salesmen’s initiatives. Sana (2011) has also developed EOQ model for similar products when the demand of the end customers depends on the stock level, selling price and sales teams’ initiatives.

The classical EMQ model assumes a continuous issuing policy for satisfying product demand. However, in real life vendor–buyer integrated supply chain environment, a multiple deliveries policy is commonly used in dealing with customer’s demands. Goyal (1977) introduced the concept and developed a framework for integrated supplier–customer inventory model. He proposed a method that is typically applicable to those inventory problems where a product is procured by a single customer from a single supplier. Some researchers (see Aderohunmu et al. 1995; Chiu et al. 2011, 2012; Cardenas-Barron et al. 2013; Taleizadeh et al. 2014, 2015a, b) addressed various coordination supply chain optimization issues extending the idea of Goyal (1977). Aderohunmu et al. (1995) achieved cost savings of both the vendor and buyer when they followed a cooperative batching policy and shared cost information along with other information in time. Chiu et al. (2011) developed an inventory model based on EMQ considering rework and multiple shipments. They optimize the replenishment lot-size using differential calculus technique. Then Chiu et al. (2012) determined the replenishment policy for the EMQ model with rework and multiple shipments through mathematical modeling approach. Cardenas-Barron et al. (2013) determined jointly both the optimal replenishment lot size and the optimal number of shipments for an EMQ model with rework and multiple shipments. Taleizadeh et al. (2015a) recently determined the optimal price, replenishment lot size and number of shipment in an EPQ model with rework and multiple shipments.

Setup cost is usually treated as a constant in the aforementioned inventory models. However, in some practical situations, setup cost can be controlled and reduced through various efforts such as worker training, procedural changes and specialized equipment acquisition. For instance, faster changeovers have been associated with lower inventory, faster throughput, shorter lead time, improved quality and lower unit cost. Quick setups are also considered an important element for successfully implementing just-in-time (JIT) production or time-based competition. Therefore, for achieving production system efficiency, reduced lot sizes alone are not sufficient, unless accompanied by corresponding setup cost reduction. Thus considerable attention has been paid to the optimal lot sizing and investments in setup cost reduction (see Hong et al. 1995; Porteus 1985; Affisco et al. 2002; Lin and Hou 2005; Hou 2007; Annadurai and Uthayakumar 2010; Priyan et al. 2015; Hall 1983). Porteus (1985) first introduced the concept and developed a framework for investing in reducing EOQ model setup cost. Affisco et al. (2002) investigated the investments in setup cost reduction and quality improvement for a joint supplier-customer system with defects produced at a known constant rate. Lin and Hou (2005) considered an inventory system with random yield in which both the setup cost and yield variability can be reduced through capital investment. Hou (2007) derived a mathematical model to investigate the effects of an imperfect production process involving capital investment on the optimal solution.

Review of literature reveals that none of the authors developed an EMQ inventory model for defective products involving imperfect production processes and rework with setup cost reduction and multiple shipments under sales teams’ initiatives-dependent demand. Therefore, this paper intends to fill this remarkable gap in the literature. A comparison of our paper with the literature is provided in Table 1.

Table 1 Comparison with the literature

In steel industries, iron ores are divergently transformed into several hundreds of finished goods through steel making processes in accordance with the stipulations made by customers. Similar patterns of production can also be observed in many petrochemical industries where items are produced through refining processes of crude oil. The costs of these industries would be dependent on the manufacturing lot-size of finished goods. It is common to all and above industries that a certain percent of produced/ordered products are of imperfect quality. Today, all the above industries are rework those imperfect products into perfect ones due to limited availability of natural resources. However, all industries have a lot of pressure to sell those reworked products to downstream channel members due to the lack of proper knowledge about inventory system. Therefore, this paper investigates the issue of an EMQ inventory system for defective products with the consideration of imperfect production processes, rework, variable setup cost and sales team’s initiatives-dependent demand in a multiple shipments policy. The main contribution of this paper is to develop a mathematical model and design an iterative solution procedure to effectively increase investment and to reduce the expected total cost for EMQ inventory system involving defective products with rework and sales team’s initiative-dependent demand in a multiple shipments policy. The objective of this paper was to achieve optimal replenishment lot-size, setup cost and the initiatives of sales team so that the total cost of system is minimized. The numerical results of this paper also indicate that it can share substantial cost savings from the setup cost reduction investment. The proposed model can be used in industries like aircraft, healthcare, automobiles, computers, textiles, footwear, printers, refrigerators, mobile phones, televisions, air conditioners, washing machines, tyres and bulk products such as printed circuit boards., etc.

The paper is designed as follows: introduction is given in Sect. 1. In Sect. 2, notation and assumptions are given. The mathematical formulation of the problem is discussed in Sect. 3. The solution procedure is given Sect. 4. Numerical and sensitivity analysis are given in Sect. 5. Finally, the conclusion of the study is summarized in Sect. 6.

Notations and assumptions

We adopt the following notations and assumptions to develop the mathematical model of the proposed problem. Additional notations and assumptions will be given out when required.

Notations

Q :

Manufacturing batch size, to be determined for each cycle, a decision variable

S :

Setup cost per cycle ($/cycle), a decision variable

$\rho$ :

Initiatives of the sales teams (measured by point scale such as 1-point, 2-points, etc.), a decision variable

$D(\rho )$ :

Demand rate of the products (units/time unit)

$D_1$ :

The first part of the demand rate which is independent of the sales teams’initiatives $(\rho )$ (units/time unit)

$D_2$ :

A scale parameter of 2nd part of the demand which varies with the sales teams’ initiatives $(\rho )$ (units/time unit)

$S_0$ :

Original setup cost (before any investment is made)

I(S):

Capital investment required to achieve setup cost S

$\tau$ :

Fractional opportunity cost of capital per unit time (e.g., interest rate)

n :

Number of fixed quantity installments of the finished batch to be delivered by request to customers

$C_\mathrm{v}$ :

Production cost ($/unit)

$C_\mathrm{r}$ :

Rework cost ($/unit)

$C_\mathrm{d}$ :

Disposal cost per scrap product ($/unit)

v :

Delivery cost per product shipped to customers ($/unit)

F :

Fixed delivery cost per shipment ($/shipment)

h :

Holding cost ($/unit/time unit)

$h_\mathrm{r}$ :

Holding cost for each reworked product ($/unit/time unit)

P :

Production rate (units/time unit)

$P_\mathrm{r}$ :

Reworking rate (units/time unit)

$\eta$ :

Cost per unit effort of the sales teams’ initiatives ($/unit)

m :

An elasticity parameter

$\alpha$ :

Defective rate, a random variable

$f(\alpha )$ :

The probability density function of $\alpha$ which follows uniform distribution

$\theta$ :

A proportion of scrap; it is assumed to be known and constant

T :

Cycle length

Assumptions

• 1. All defective products produced are detected after the production cycle is over, and rework cost for defective products will be incurred.

• 2. The rate of demand is an increasing function of sales teams’ initiatives and the sales teams’ initiatives is a discrete decision variable.

• 3. The relationship between setup cost reduction and capital investment can be described by the logarithmic investment cost function. That is,

  $$\begin{aligned} I(S) = M \mathrm{ln} \left( \frac{S_0}{S}\right) \quad \mathrm{for}\quad 0 \; < \; S \le \; S_0 \end{aligned}$$

  where $M = 1/\delta$, and $\delta$ is the percentage decrease in S per dollar increase in I(S). This function is consistent with the Japanese experience as reported in Hall (1983) and has been utilized in many researches (e.g. Porteus 1985 and others).

• 4. Fixed quantity multiple installments of the finished batch are delivered to customers at a fixed interval of time and there is no shortage in the system.

Mathematical model formulation

In the EMQ inventory system, the rate of demand for the final customers is given by the following expression:$D(\rho )=D_1+D_2\left( 1-\frac{1}{(1+\rho )}\right)$ which is similar to Crdenas-Barrn et al. (2014). The first part of the demand $(D_1)$ is independent of the sales teams’ initiatives. On the other hand, the second part of the demand is a bounded increasing function of $\rho ;$ unlike the unbounded function of $\rho.$ Here, $D\rightarrow (D_1+D_2)$ when $\rho \rightarrow \infty;$ and $D\rightarrow D_1$ when $\rho \rightarrow 0.$ It is important to remark that the term $D_1$ tends to zero when new products are launched into the market. In this case, the demand of the product is zero when $\rho \rightarrow 0,$ i.e., the quality and prices are not familiar to the customers; whereas the demand of the familiar products is already increased by promotional efforts such as free gifts, better services, discounts, delay in payments, etc. The units of $\rho$ is measured by the volume of the efforts made by the sales teams like the number of efficient salesmen and the above promotional efforts. It does not have any traditional units but it is measured by point scale such as 1-point, 2-point, 3-point, etc. In practice, larger point scale includes more promotional effort that results in higher cost (Crdenas-Barrn et al. 2014). Then the cost of sales teams’ initiatives $(\rho )$ is given by $\eta \rho ^m$, where η (>0) is a scale parameter and m (>0) is the elasticity parameter.

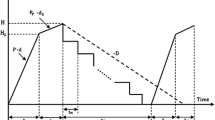
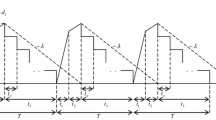
Consider a manufactured product has an annual demand rate $D(\rho )$ and this product can be produced at a finite production rate P. The process may randomly generate a portion $\alpha$ of defective products at a production rate d. All produced products are screened 100 % and inspection cost is included in the unit production cost $C_\mathrm{v}$. All produced defective products are reworked immediately at a finite rate $P_\mathrm{r}$ after the regular process ends. A portion $\theta$ (where $0< \theta < 1$) of reworked items fails and becomes scrap. To prevent a shortage from occurring, the production rate P is assumed to be larger than the sum of demand rate D and production rate of defective products d. That is: $(P-d-D)>0$ or $(1-\alpha - D/P)>0$; where d can be expressed as $d=P\alpha$. Let $d_1$ denote the production rate of scrap items during the rework process, then $d_1$ can be expressed as: $d_1=P_\mathrm{r}\theta$. It is further assumed that a multiple shipment policy is employed and the finished items can only be delivered to customers if the whole lot is quality assured at the end of rework. Fixed quantity n installments of a finished batch are delivered to customers at a fixed interval of time during production downtime $t_3$. The on-hand inventory level of perfect quality products during $t_3$ is depicted in Fig. 1.

Fig. 1

On-hand inventory of perfect quality products in the proposed EMQ model

In Fig. 1, $H_1$ = the maximum level of on-hand inventory in units when regular production process ends, H = the maximum level of on-hand inventory in units when the rework process finishes, $t_1$ = the production uptime for the proposed EMQ model, $t_2$ = time required for reworking of defective products, $t_3$ = time required for delivering all quality assured finished products and $t_n$ = a fixed interval of time between each installment of finished products delivered during production downtime $t_3$.

The production cycle length $T=t_1+t_2+t_3$ and the following equations can be obtained directly from Fig. 1 (for more see Hayek and Salameh 2001; Chiu et al. 2011): $H_1=(P-d)t_1=(P-d)\frac{Q}{P}=(1-\alpha )Q$

$H=H_1+(P_\mathrm{r}-d_1)t_2 = Q(1-\theta \alpha )$

$t_1=\frac{Q}{P}=\frac{H_1}{P-d}$

$t_2=\frac{\alpha Q}{P_\mathrm{r}}$

$t_3=nt_n=T-(t_1+t_2)=Q\left( \frac{(1-\theta \alpha )}{D}-\frac{1}{P}-\frac{\alpha }{P_\mathrm{r}} \right)$

The on-hand inventory of defective products during production uptime $t_1$ and rework time $t_2$ is depicted in Fig. 2. One notes that maximum level of on-hand defective products is $dt_1$, and a portion $\theta$ of reworked products fails during the reworking and becomes scrap. Therefore, total number of scrap products are $\theta dt_1$, where

$$dt_1=P\alpha t_1=\alpha Q$$

$$\theta dt_1=\theta P\alpha t_1=\theta \alpha Q$$

Fig. 2

On-hand inventory of defective products in the proposed EMQ model

Hence, based on the above description, the long-run average total cost denoted by $\Pi$ which is sum of production costs, cost of sales teams’ initiatives, fixed setup cost, rework costs, disposal costs, delivery costs, holding cost for items reworked, holding cost during uptime $t_1$ and reworking time $t_2$, and holding cost for finished goods during the delivery time $t_3$ can be obtained as Chiu et al. (2011) is

$$\begin{aligned} \Pi&=\frac{(S+\eta \rho ^m+nF)D}{Q(1-\theta E[\alpha ])}+\frac{D\left( C_\mathrm{v}+C_\mathrm{r}E[\alpha ] +C_\mathrm{d}E[\alpha ]\theta \right) }{(1-\theta E[\alpha ])} \\ &\quad +\frac{hQD}{2P_\mathrm{r}(1-\theta E[\alpha ])}\{2E[\alpha ] -(E[\alpha ])^2-\theta (E[\alpha ])^2\}+\frac{hQD}{2P(1-\theta E[\alpha ])}+vD +\frac{h_\mathrm{r}\left( E[\alpha ]\right) ^2QD}{2P_\mathrm{r}(1-\theta E[\alpha ])}\nonumber \\&\quad +\left( \frac{n-1}{n}\right) \left[ \frac{hQ(1-\theta E[\alpha ])}{2}-\frac{hQD}{2P}-\frac{hQE[\alpha ]D}{2P_\mathrm{r}}\right] \end{aligned}$$

(1)

Now we consider the defective rate $\alpha$ follows uniform distribution with mean $E(\alpha )=\frac{a+b}{2}$ where $a>0, b>0$ and $a<b$.

Using $E(\alpha )=\frac{a+b}{2}$, Eq. (2) can be re-written as

$$\begin{aligned} \Pi&=\frac{2(S+\eta \rho ^m+nF)D}{Q\left\{ 2-\theta (a+b)\right\} }+\frac{2D}{\left\{ 2-\theta (a+b) \right\} } \\ &\quad \left\{ C_\mathrm{v} +C_\mathrm{r} \left( \frac{a+b}{2}\right) +C_\mathrm{d} \left( \frac{a+b}{2}\right) \theta \right\} \nonumber \\&\quad +\frac{hQD}{P_\mathrm{r}\left\{ 2-\theta (a+b)\right\} } \left[ (a+b)- \left( \frac{a+b}{2}\right) ^2 (1+\theta )\right] \\ &\quad +\frac{h Q D}{P\left\{ 2-\theta (a+b) \right\} }+v D \nonumber \\&\quad +\frac{h_\mathrm{r} (a+b)^2QD}{4P_\mathrm{r}\left\{ 2-\theta (a+b)\right\} } +\frac{hQD}{2}\left( \frac{n-1}{n}\right) \\ &\quad \left[ \frac{\left\{ 2-\theta (a+b)\right\} }{2D}-\frac{1}{P} -\frac{(a+b) }{2P_\mathrm{r}}\right] \end{aligned}$$

(2)

In order to accommodate a more realistic inventory situation, we seek to add the effects of investment cost function for setup cost reduction. That is, we assume that the capital investment I(S) in reducing setup cost is a logarithmic function of the setup cost S. The investment required to reduce the setup cost from original level $S_0$ to a target level S, where I(S) is a convex and strictly decreasing function. Here, investment I(S) is the one-time investment cost whose benefits will extend indefinitely into the future. Thus the annual cost of such an investment is $\tau I(S),$ where $\tau$ is the annual fractional cost of capital investment (e.g., interest rate).

Hence, our objective is to minimize the new long-run average total cost per unit time denoted by $\hat{\Pi }$, namely the sum of the capital investment cost for reducing S and the inventory relevant cost as expressed in (2), by optimizing over Q, S and $\rho$ constrained on $0 \;< S \; \le \; S_0$. Then the long-run average total cost per unit time for the system becomes

$$\begin{aligned} \hat{\Pi }&=\tau I(S)+ \Pi \nonumber \\&=\tau M \mathrm{ln} \left( \frac{S_0}{S}\right) +\frac{2(S+\eta \rho ^m+nF)D}{Q\left\{ 2-\theta (a+b)\right\} } \\ &\quad +\frac{2D}{\left\{ 2-\theta (a+b) \right\} }\left\{ C_\mathrm{v} +C_\mathrm{r} \left( \frac{a+b}{2}\right) +C_\mathrm{d} \left( \frac{a+b}{2}\right) \theta \right\} \nonumber \\&\quad +\frac{hQD}{P_\mathrm{r}\left\{ 2-\theta (a+b)\right\} } \left[ (a+b)- \left( \frac{a+b}{2}\right) ^2 (1+\theta )\right] \\ &\quad +\frac{h Q D}{P\left\{ 2-\theta (a+b) \right\} }+v D \nonumber \\&\quad +\frac{h_\mathrm{r} (a+b)^2QD}{4P_\mathrm{r}\left\{ 2-\theta (a+b)\right\} } +\frac{hQD}{2}\left( \frac{n-1}{n}\right) \\ &\quad \left[ \frac{\left\{ 2-\theta (a+b)\right\} }{2D}-\frac{1}{P} -\frac{(a+b) }{2P_\mathrm{r}}\right] \end{aligned}$$

(3)

constrained on $0 \;< S \; \le \; S_0$.

Now, if the rework process is assumed to be perfect, i.e. $\theta \; = \; 0$. In other words, all reworked products are repaired, then it may be noted that during the rework time $t_2$ the slope is $P_\mathrm{r}$ instead of $(P_\mathrm{r} - d_1)$. Hence, the long-run average total cost per unit time given in Eq. (3) reduces to

$$\begin{aligned} \hat{\Pi }&=\tau M \mathrm{ln} \left( \frac{S_0}{S}\right) +\frac{(S+\eta \rho ^m+nF)D}{Q} \\ &\quad +D\left\{ C_\mathrm{v} +C_\mathrm{r} \left( \frac{a+b}{2}\right) +v\right\} +\frac{h Q D}{2P} \nonumber \\&\quad +\frac{hQD}{2P_\mathrm{r}} \left[ (a+b)- \left( \frac{a+b}{2}\right) ^2\right] +\frac{h_\mathrm{r} (a+b)^2QD}{8P_\mathrm{r}} \\ &\quad +\frac{hQD}{2}\left( \frac{n-1}{n}\right) \left[ \frac{1}{D}-\frac{1}{P} -\frac{(a+b) }{2P_\mathrm{r}}\right] \end{aligned}$$

constrained on $0 \;< S \; \le \; S_0$.

On the other hand, the problem of EMQ inventory system for defective products with rework and variable setup cost under sales teams’ initiatives-dependent demand can be mathematically formulated by

$$\begin{aligned} \mathrm{Min}\,\hat{\Pi }&=\tau M \mathrm{ln} \left( \frac{S_0}{S}\right) +\frac{2(S+\eta \rho ^m+nF)D}{Q\left\{ 2-\theta (a+b)\right\} } \\ &\quad +\frac{2D}{\left\{ 2-\theta (a+b) \right\} }\left\{ C_\mathrm{v} +C_\mathrm{r} \left( \frac{a+b}{2}\right) \right. \nonumber \\&\quad \left. +C_\mathrm{d} \left( \frac{a+b}{2}\right) \theta \right\} +\frac{hQD}{P_\mathrm{r}\left\{ 2-\theta (a+b)\right\} } \\&\quad \left[ (a+b)- \left( \frac{a+b}{2}\right) ^2 (1+\theta )\right] \\ &\quad +\frac{h Q D}{P\left\{ 2-\theta (a+b) \right\} } \\&\quad +v D+\frac{h_\mathrm{r} (a+b)^2QD}{4P_\mathrm{r}\left\{ 2-\theta (a+b)\right\} } \\ &\quad +\frac{hQD}{2}\left( \frac{n-1}{n}\right) \\ &\quad \left[ \frac{\left\{ 2-\theta (a+b)\right\} }{2D}-\frac{1}{P} -\frac{(a+b) }{2P_\mathrm{r}}\right] \nonumber \\ \mathrm{Subject\,to}&\,0 \;< S \; \le \; S_0. \end{aligned}$$

(4)

Solution procedure

In order to find the minimum cost for this non-linear programming problem, ignore the constraint $0\; < S \; \le \; S_0$ for the moment and minimize the total relevant cost function over Q, S and $\rho$ with classical differential calculus optimization techniques.

Proposition 1

For fixed Q and S, $\hat{\Pi }$ is convex in $\rho$.

Proof

Taking the first and second partial derivatives of $\hat{\Pi }$ with respect to $\rho$, we have

$$\begin{aligned} \frac{\partial \hat{\Pi }}{\partial \rho } =m\rho ^{m-1} \end{aligned}$$

and

$$\begin{aligned} \frac{\partial ^2 \hat{\Pi }}{\partial \rho ^2} =m(m-1)\rho ^{m-2}>0. \end{aligned}$$

Therefore, for fixed Q and S, $\hat{\Pi }$ is convex in $\rho$ This completes the proof of Proposition 1. $\square$

Now for fixed $\rho$, taking the first partial derivatives of $\hat{\Pi }$ with respect to Q and S, respectively, we obtain

$$\begin{aligned} \frac{\partial \hat{\Pi }}{\partial Q}&=-\frac{2(S+\eta \rho ^m+nF)D}{Q^2\left\{ 2-\theta (a+b)\right\} }+\frac{hD}{P_\mathrm{r}\left\{ 2-\theta (a+b)\right\} } \left\{ (a+b)- \left( \frac{a+b}{2}\right) ^2 (1+\theta )\right\} \nonumber \\&\quad +\frac{h D}{P\left\{ 2-\theta (a+b) \right\} }+\frac{h_\mathrm{r} (a+b)^2D}{4P_\mathrm{r}\left\{ 2-\theta (a+b)\right\} }+\frac{GhD}{2} \end{aligned}$$

(5)

and

$$\begin{aligned} \frac{\partial \hat{\Pi }}{\partial S} =-\frac{\tau M}{S}+\frac{2D}{Q(2-\theta (a+b))} \end{aligned}$$

(6)

To simplify notation, we define $G = \left( \frac{n-1}{n}\right) \left[ \frac{\left\{ 2-\theta (a+b)\right\} }{2D}-\frac{1}{P} -\frac{(a+b) }{2P_\mathrm{r}}\right].$

Then, by examining the second-order sufficient conditions (SOSC), it can be verified that $\hat{\Pi }$ is a convex function of Q and S for fixed $\rho$.

On the other hand, for a given value of $\rho$, by setting Eqs. (5) and (6) equal to zero, we obtain

$$\begin{aligned} Q=\left\{ \frac{4(S+\eta \rho ^m+nF)}{h\left[ \frac{2}{P}+\frac{(a+b)^2h_\mathrm{r}}{2hP_\mathrm{r}}+\frac{2}{P_\mathrm{r}}\left\{ (a+b)- \left( \frac{a+b}{2} \right) ^2 (1+\theta )\right\} +G(2-\theta (a+b))\right] }\right\} ^{1/2} \end{aligned}$$

(7)

and

$$\begin{aligned} S=\frac{Q\tau M(2-\theta (a+b))}{2D} \end{aligned}$$

(8)

respectively.

Theoretically, for fixed $\rho$, by solving Eqs. (7) and (8), we can obtain the values of Q and S (denote these values by $Q^{*}$ and $S^{*}$, respectively). The following proposition asserts that, for fixed $\rho$, when the constraint $0 \;< S \; \le \; S_0$ is ignored, the point ($Q^{*}$, $S^{*}$) is the optimal solution such that the expected total cost $\hat{\Pi }$ has minimum value.

Proposition 2

For fixed $\rho$, the Hessian matrix for $\hat{\Pi }$ is positive definite at point $(Q^{*}$, $S^{*})$.

Proof

See Appendix.

Now we consider the constraint $0 \;< S \; \le \; S_0$. From Eq. (8), we note that S is positive, as the parameters $\tau,\, M,\, Q,\, D$ are positive and $0\;<\theta <1, 0\;<a\;<1$ and $0\;<b\;<1$ . Also, if $S^{*} \; < \; S_0$, then ($Q^{*}$, $S^{*}$) is an interior optimal solution. On the other hand, if $S^{*} \ge S_0$, then it is unrealistic to invest in reducing setup cost; in this situation, the optimal $S^{*} = S_0$.

Based on the convexity behavior of objective function with respect to the decision variables, the following algorithm is designed to find the optimal values for the Q, S and $\rho$; the flowchart of the algorithm is also illustrated in Fig. 3.

Fig. 3

Computer flowchart of algorithm

Algorithm 1

• Step 1. Set the initiatives of the sales teams $\rho =0$.

• Step 2. Repeat step (1.1)–(1.3) until no change occurs in the values of Q and S. Denote the solution by $(\dot{Q},\dot{S})$.

  • Step 2.1. Start with $S_1=S_0$.

  • Step 2.2. Substituting $S_1$ into Eq. (7) evaluates $Q_1$.

  • Step 2.3. Utilizing $Q_1$ determines $S_2$ from Eq. (8).

• Step 3. Compare $\dot{S}$ with $S_0$

  • (i) If $\dot{S} < S_0$, go to step (3).

  • (ii) If $\dot{S} > S_0$, then set $\dot{S} = S_0$ and utilize Eq. (7) (replace S by $S_0$) to determine the new $\dot{Q}$, then go to step (4).

• Step 4. Compute the corresponding $\hat{\Pi }_{(\rho )}$ using Eq. (4).

• Step 5. Set $\rho =\rho +1$, repeat Step 2–4 to get $\hat{\Pi }_{(\rho )}$.

• Step 6. If $\hat{\Pi }_{(\rho )}\le \hat{\Pi }_{(\rho -1)}$, then go to Step 5; otherwise goto Step 7.

• Step 7. Set $(Q^*, S^*, \rho ^*)= (\dot{Q}, \dot{S}, \rho -1)$, then $\hat{\Pi }_{(Q^*,S^*,\rho ^*)}$ is the minimum long-run average total cost, and $(Q^*, S^*,\rho ^*)$ is the optimal solution for the proposed EMQ inventory problem.

Numerical analysis

In this section, a numerical example is given to illustrate the above solution procedure. The solutions to this example is obtained using the computer MatLab software.

The values of the following parameters are almost similar to those used in Chiu et al. (2011): $P=60{,}000$ units/year, $D_1 = 3400$ units/year, $D_2=5$ units/year, $P_\mathrm{r}=2200$ units/year, $\theta = 0.1$, $C_\mathrm{v}=\$100$/unit, $F=\$4350$/shipment, $v=0.1$/unit, $C_\mathrm{r}=\$60$/unit, $C_\mathrm{d}=\$20$/unit, $h=\$20$/unit/year, $h_\mathrm{r}=\$40$/unit/year, $\eta =\$50$/unit $m=1$, a = 0.15, b = 0.25 and $n =4$ installments of the finished batch are delivered per cycle. In addition, for setup cost reduction EMQ inventory system, we take and $\tau$ = 0.1 per dollar per year. In Chiu et al. (2011) model, they considered the setup cost $S = \$20{,}000$ per production run. Therefore, we solve the Logarithmic investment case for which the initial setup cost $S_0 = 20{,}000$.

Now, applying the proposed algorithm for different parameter of investment function $M = 7250, 5800$ and 4350, the results of the solution procedure are summarized in Table 2. Here also, the results of the no-investment policy in the same table are listed to illustrate the effects of setup cost reduction.

Table 2 Summary of optimal solution

Sensitivity analysis

To further illustrate the model and algorithm, we now study the effects of parameters $D_1, P$ and $P_\mathrm{r}$ on the optimal replenishment lot-size $Q^*$, setup cost $S^*$, the initiatives of sales teams $\rho ^*$ and the minimum long-run average total cost $\hat{\Pi }$. The sensitivity analysis is performed by changing the parameters of $D_1, P$ and $P_\mathrm{r}$ by +50, +25,$-$25 and $-$50 %. The results are presented in Tables 2, 3 and 4 and the corresponding curves of the average total cost are plotted in Fig. 4. In addition, the sensitivity analysis of $\theta$ is shown in Table 5 and the graphic of the average total cost $\hat{\Pi }$ for distinct value of $\theta$ is depicted also in Fig. 4.

Fig. 4

Graphic of average total cost for distinct $D_1,P, P_\text{r}$ and $\theta$

Table 3 Effects of demand on optimal solution

Table 4 Effects of production rate on optimal solution

Table 5 Effects of reworking rate on optimal solution

Table 6 Effects of $\theta$ on optimal solution

Managerial implications

There are some interesting managerial implications in the above analyses. We make the following observations:

• 1. From Table 2, we can recognize that a decrease in the first part of demand rate $D_1$ tends to reduce the optimal replenishment lot-size Q and long-run average total cost $\hat{\Pi }$, but it is interesting to note that the optimal setup cost S increases.

• 2. Table 3 shows that when the production rate P decreases, the optimal replenishment lot-size Q and setup cost S also decrease but the long-run average total cost $\hat{\Pi }$ increases without affecting the initiatives of sales teams $\rho$.

• 3. Generally, we spend large amount of money to setup if we rework the large amount of quantity. Similarly, we spend small amount of money to setup if we rework the small amount of quantity. In view of this the setup time or cost may be depend on rework rate. The present analyses proved this general fact. That is, Table 4 shows that when rework production rate $P_\mathrm{r}$ decreases, the setup cost S and replenishment lot-size Q decrease, but the long-run average total cost $\hat{\Pi }$ increases.

• 4. We can observe that if the proportion of scrap rate $\theta$ increases, then the long-run average total cost $\hat{\Pi }$ increases (see Tables 5, 6). This fact is expected, because, in practice, if the manufacturing company’s scrap rate is large, then the company may lose large amounts of money. Therefore, we can say that the proposed mathematical modeling and computational algorithm may applicable for real life marketing.

• 5. The analyses show that if we add the mathematical investment function $I(S) = M \mathrm{ln} \left( \frac{S_0}{S}\right)$ in objective function, then the significant savings can be easily achieved.

Conclusion

Industrial engineering is a branch of engineering which deals with the optimization of complex processes or systems. It is concerned with the development, improvement, implementation and evaluation of integrated systems of people, accounting, inventory management, marketing, financial analysis, information, decision making, customer services, operations, financial management and marketing strategies, as well as the mathematical and physical together with the principles and methods of engineering design to specify, predict and evaluate the results to be obtained from such systems or processes. This study developed a mathematical model for a defective product involving imperfect production processes and rework with variable setup cost in a multiple shipments inventory system. Here we assumed that the demand is dependent on sales team's initiatives. Mathematical modeling is employed here, and the long-run average function is derived and proved to be convex. We offered strategic decision-making to achieve optimal replenishment lot-size, setup cost and the initiatives of sales teams so that the total cost of system is minimized. Numerical example and sensitivity analyses are given to demonstrate the application and the performance of the proposed methodology.

There are several extension of this work that could constitute future research related to this field. One immediate probable extension could be to discuss the effect of shortage. Also, we can consider multi-echelon supply chains such as single buyer multiple-vendor, multiple-buyer single-vendor and multiple-buyer multiple-vendor systems. Furthermore, some of parameter of the model may be either fuzzy or random variable. In this case, the model has either fuzzy or stochastic nature.

Appendix

We want to prove the Hessian Matrix of $\hat{\Pi }$ at point $(Q^*,S^*)$ for fixed $\rho$ is positive definite. We first obtain the Hessian matrix H as follows:

$$\begin{aligned} {\mathbf H} =\left[ \begin{array}{cc} \frac{\partial ^2\hat{\Pi }}{\partial Q^2}&{} \frac{\partial ^2\hat{\Pi }}{\partial Q \partial S} \\ \frac{\partial ^2\hat{\Pi }}{\partial S\partial Q}&{} \frac{\partial ^2\hat{\Pi }}{\partial S^2} \end{array}\right] \end{aligned}$$

where

$$\begin{aligned} \frac{\partial ^2 \hat{\Pi }}{\partial Q^2}&=\frac{4(S+\eta \rho ^m+nF)D}{Q^3\left\{ 2-\theta (a+b)\right\} },\\ \frac{\partial ^2\hat{\Pi }}{\partial Q \partial S}&=\frac{\partial ^2\hat{\Pi }}{ \partial S \partial Q}=-\frac{2D}{ Q^2(2-\theta (a+b))},\\ \frac{\partial ^2 \hat{\Pi }}{\partial S^2}&=\frac{2\tau M}{S^2}. \end{aligned}$$

Then we proceed by evaluating the principal minor determinants of H at point $(Q^*,S^*)$. The first principal minor determinant of H is

$$\begin{aligned} |H_{11}|=\frac{4D}{Q^{*3}}\left[ \frac{(S+\eta \rho ^m+nF)}{\left\{ 2-\theta (a+b)\right\} }\right] \quad \quad \quad \quad ({\rm A}1) \end{aligned}$$

The second principal minor of H is

$$\begin{aligned} |H_{22}|&=\frac{4D}{Q^{*3}}\left[ \frac{(S+\eta \rho ^m+nF)}{\left\{ 2-\theta (a+b)\right\} }\right] \frac{2\tau M}{S^2}+\frac{2D}{ Q^{*2}(2-\theta (a+b))}\nonumber \\&>0. \quad \quad \quad \quad ({\rm A}2) \end{aligned}$$

Therefore, from (A1)-(A2), it is clearly seen that the Hessian matrix H is positive definite at point $(Q^*,S^*)$.

The proof is completed. $\square$