Introduction

Evidence of damages in previous earthquakes has shown that damage to structures is increased when structures become closer to earthquake faults called near-field earthquake effect. This effect has been recognized after the 1971 San Fernando earthquake (Singh 1985). In the early stage, the proximity of structure to the site was considered as the main parameter. Later, more studies on the property of the near-field records have shown that existence of strong velocity pulses in ground motion records due to fault rupture directivity effects is a more important parameter in this effect (Alavi and Krawinkler 2001; Hall et al. 1995; Luco and Cornell 2007). The effect of pulses on increasing the linear and non-linear demand of structures has been studied in numerous studies such as Chopra and Chintanapakdee (2001) and Choi et al. (2005).

Although the existence of pulses in the records is considered as the major reason for the near fault effect, most of existing records in databases does not have pulses in the ground motions. The existence of the pulse is identified through visual study of records. Recently, a wavelet method was utilized to identify the pulses by Baker (2007), and used in PEER strong motion database to classify the ground motion records to pulse like and non-pulse like records. Number of ground motion records of earthquake with magnitude higher than 5 in PEER database are shown in Table 1. Records are classified according to their proximity and existence of pulses. A quick look at the number of earthquake records demonstrate that out of 302 near fault earthquakes (distance <15 km), only 109 have pulses in one or two components of earthquake. Therefore, in a real situation, when structures are located in the near fault location, it is more probable to expose to a non-pulse like records. So, it is required to have a realistic approach to evaluate the behavior of structures in the near-field earthquakes.

Table 1 Number of strong ground motion records (M > 5) in PEER database and their classification in terms of distance and existing of pulses
Full size table

The main objective of this study is to compare the probability of different damage state of low-rise moderate ductility concrete moment resistant frame in the near- and far-field earthquakes. These types of frames are commonly built in rural and most of the small and mid-size cities in Iran, which are mostly located near faults. Since special provision for near-field earthquake does not exist in the Iranian design code, an accurate evaluation of behavior of these buildings in the near-field is required. For this purpose, two frames with two and three stories are considered, and fragility functions of structures are evaluated in the near- and far-field. A mix of pulse and non-pulse like records are selected for evaluation of fragility function in the near-field. The probability of failure of frames in two different high seismic regions in Iran were evaluated and compared.

Evaluation of probability of damages

The probability of failures of structures is widely used recently to evaluate the behavior and performance of structures. This method was adopted by combining probabilistic response of structures and probability of earthquake occurrence. Based on this combination, the exceeding probability of structural damage from given damage level (D > d i ) is estimated by Eq. 1 (Nasserasadi 2006).

$$ P(D > d_{i} ) = - \int\limits_{0}^{\infty } {F(D > d_{i} |{\text{im}})\,\tfrac{{d[F({\text{im)}}]}}{{d({\text{im)}}}}\,d({\text{im}})} $$
(1)

where, F(D > d i |im) is the conditional probability of exceeding of damage (D) from a certain level of damage (d i ) in given earthquake intensity (im) called fragility function, and F(im) is probability of exceeding hazard from given intensity of (im) called hazard function. The hazard function is related to the seismicity of region and estimated by probabilistic approach. This function for any region can be presented by simple mathematical function of P = K 0im–K (Jalayer 2003), where K 0 and K are constant values that can be estimated for each site by fitting the function to the hazard curve. im is the intensity measure parameter which can be peak ground acceleration (PGA), peak ground velocity or peak ground displacement. Fragility function, given by Eq. 2, demonstrates the structural behavior in the risk formulation and estimated by either empirical or analytical methods.

$$ P(D > d_{i} |{\text{im}}) = \varPhi \left( {{\raise0.7ex\hbox{${\ln \left( {{\text{im}}/\overline{{{\text{IM}}_{i} }} } \right)}$} \!\mathord{\left/ {\vphantom {{\ln \left( {{\text{im}}/\overline{{{\text{IM}}_{i} }} } \right)} {\mathop \beta \nolimits_{i} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\mathop \beta \nolimits_{i} }$}}} \right) $$
(2)

where, Φ is standard cumulative normal distribution function, \( \overline{{{\text{IM}}_{i} }} \) is median of im for ith damage state (i.e., an IM with 50 % chance of exceeding damage from d i ), and β i is logarithmic natural standard deviation of ground motion intensity in damage state of d i (sometimes referred to as the dispersion of fragility). The probability of exceeding damage from a given damage state [P (D > d i )] is estimated by putting the fragility and hazard function in Eq. 1. The result was solved in close form and given in Eq. 3 (Nasserasadi 2006).

$$ P(D > d_{i} ) = K_{0} {\text{IM}}_{i}^{ - K} \,\mathop e\nolimits^{{\frac{{\mathop {\beta_{i} }\nolimits^{2} \mathop K\nolimits^{2} }}{2}}} $$
(3)

For assessing damages in structures, four damage states are usually considered; slight, moderate, extensive and complete (HAZUS 1999). The damage state in empirical studies is defined by quantifying damage in the structures and analytical studies, where damage defined by a damages indexes such as inter-story drift (ISD), are defined by assuming different values to damages indexes. Since little empirical information is available for most of the modern structures, fragility functions are developed by analytical methods. In this method, it is required to evaluate the distribution of damage index in different im and estimate the probability of exceeding of damage from each damage threshold (Nasserasadi et al. 2009).

Methodology of study

To investigate seismic risk of short reinforced concrete moment frames with moderate ductility in the near- and far-field earthquakes, two moderate ductility reinforced concrete moment frames with two and three story have been chosen and designed. The seismic fragility function of frames are estimated by analytical methodology (see Nasserasadi et al. 2009) using near- and far-field earthquake records separately, and the exceeding probability of damage from different damage states are estimated for two different major cities and used for comparison of safety of frames. The details of each stage are given in following sections.

Selection and design of frames

Two frames, which selected from the middle frame of a three bays building, with two and three stories were selected. Frames were designed according to the 3rd edition of Iranian code of practice for seismic resistant design of building (Building and Housing Research Center 2005) for soil type I (rock or hard soil), and very high seismic zone and the Iranian National Building Code, Division 9 (2009). The dead and live loads of floor were taken as 6.9 and 2 KN/m2, respectively; the dead and live loads of the roof were taken as 6.4 and 1.5 KN/m2, respectively. The elevations of selected frames are shown in Fig. 1. Designed sections are given in Table 2.

Fig. 1
figure 1

Elevation view of two and three story frames used in this study

Full size image
Table 2 Designed sections for beams and columns of selected frames
Full size table

Modeling of frames

OPENSEES software (Mazzoni et al. 2007) was used for nonlinear dynamic analysis of structures. Plastic hinges in all the beams and columns was modeled by fiber elements. In each section, a mesh of 12 × 12 fiber was defined and divided into two parts: (1) the cover; modeled as unconfined concrete with two fiber mesh in the outer side of section and (2) the core; modeled as confined concrete with 8 × 8 fiber mesh. The methodology of Reddiar (2009) was used for modeling the constitutional behavior of confined concrete. Stress–strain of longitude reinforcement was considered as elastoplastic bilinear material with strength hardening ratio of 1 %. Typical material behavior of steel and concrete fibers is shown in Fig. 2. The yielding stress of steel was taken as 400 MPa and multiplied by 1.15 according to FEMA 356 (2000) guideline, and the strength of concrete was taken as 21 MPa.

Fig. 2
figure 2

Constitutional behavioral model of concrete and steel fibers in OPENSEES model. a Typical confined and non-confined model of concrete fibers (adopted after Reddiar and Karthic 2009). b Typical bi-linear model of longitudinal steel fibers

Full size image

Selection of damage index and evaluation of its distribution

For assessing the damage in structure, the most used damage index which is ISD was chosen. This index directly related to damage in structure and non-structural component (Porter 2000). The thresholds of different damage state were chosen from the HAZUS’s recommendations (HAZUS 1999) given in Table 3.

Table 3 The threshold of inter-story drift for different damage states
Full size table

The distribution of damage index, which is required for fragility development, was evaluated by multi-stripe analysis. In this method, the structures were analyzed subject to several records with increasing intensity, and the distribution of response on each intensity measure was evaluated. In this study, to evaluate the distribution of response in far- and near-field earthquakes, two sets of records were chosen from PEER (2012) strong ground motion database with magnitude equal or >5 that recorded soil type I. Earthquakes with fault-to-site distance <15 km were considered as near-field, and higher than 15 were considered as far-field. The near-field records consisted of pulse like and non-pulse like records to incorporate the possibility of being expose to the impulsive effect of near-field records. The lists of selected near- and far-field earthquakes are given in Tables 4 and 5, respectively. In Fig. 3, the median of selected records are compared with design spectrum of soil type I of Iranian seismic code. As it is observed, selected records have good consistency with the design spectrum in the range of studied frames, which is low period range.

Table 4 Selected near-field records
Full size table
Table 5 Selected far-field records
Full size table
Fig. 3
figure 3

Comparison of mean response spectrums of near- and far-field of earthquakes with standard design spectrum of the soil type I of Iranian seismic code. The period of two (T = 0.53 s) and three story (T = 0.72 s) frame are highlighted in the spectra

Full size image

The PGA was consider as the intensity measure in this study and the records were scaled to different values of PGA, and the maximum inter-story response of structures was evaluated by non-linear analysis of structure subjected to all records and different level of PGAs. The distribution of ISD has been evaluated for near- and far-field earthquakes as shown in Figs. 4 and 5, respectively. Each point on this diagram represents the maximum ISD calculated in non-linear dynamic analysis of each frame. Different levels of damage states are shown in the horizontal lines.

Fig. 4
figure 4

Dynamic distribution of frame response under the effect of near-field earthquakes. Different damage thresholds are shown by horizontal lines

Full size image
Fig. 5
figure 5

Dynamic distribution of frame response under the effect of far-field earthquakes. Different damage thresholds are shown by horizontal lines

Full size image

Evaluation of fragility functions

The exceeding ISD from different damage threshold demonstrates the damage of structure at that earthquake level which can be observed in Figs. 4 and 5 (dotes over the horizontal lines). The distribution of ISD in each PGA can be considered as log-normal distribution (Kennedy et al. 1980). The exceeding probability which is called value of fragility function in each PGA was estimated by Eq. 4, which is derived from the basic probability theorem.

$$ P(D > d_{i} |{\text{PGA}}) = 1 - P(D \le d_{i} |{\text{PGA}}) = 1 - \varPhi \left( {{{\ln \left( {{{{\text{ISD}}_{i} } \mathord{\left/ {\vphantom {{{\text{ISD}}_{i} } {{\text{I}}\mathop {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{{\rm S}} }\limits^{{}} {\text{D}}_{\text{PGA}} }}} \right. \kern-0pt} {{\text{I}}\mathop {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{{\rm S}} }\limits^{{}} {\text{D}}_{\text{PGA}} }}} \right)} \mathord{\left/ {\vphantom {{\ln \left( {{{{\text{ISD}}_{i} } \mathord{\left/ {\vphantom {{{\text{ISD}}_{i} } {{\text{I}}\mathop {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{{\rm S}} }\limits^{{}} {\text{D}}_{\text{PGA}} }}} \right. \kern-0pt} {{\text{I}}\mathop {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{{\rm S}} }\limits^{{}} {\text{D}}_{\text{PGA}} }}} \right)} {\beta_{\text{PGA}} }}} \right. \kern-0pt} {\beta_{\text{PGA}} }}} \right) $$
(4)

where, \({\text{I}}\mathop {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{{\rm S}} }\limits^{{}} {\text{D}}_{\text{PGA}} \) and βPGA are the median and deviation of log-normal distribution of ISD in each PGA, ISD i is threshold of different damage state and Φ is normal cumulative function. This value of fragility function was estimated at every PGA. To from the fragility function from the estimated fragility values, a cumulative log-normal distribution function shown in Eq. 2 was fitted to the results and the fitting parameters are given in Table 6. The results of near- and far-field fragility functions are shown for different damage state in Fig. 6. To verify the results, fragility function of HAZUS (1999) for low-rise concrete frames are shown in the figure as well. The estimated fragility is very close to HAZUS fragility. It can be observed that the fragility function of far-field and near-field are very close to each other, which suggest that the damage probability of frame are close in near- and far-field earthquakes.

Table 6 The fitted fragility function parameters for fragility value of near- and far-field earthquakes
Full size table
Fig. 6
figure 6

Comparison of fragility curves of studied frames in near- and far-field of earthquake with HAZUS fragility curve for low-rise concrete structures. a Slight, b moderate, c extensive, d complete

Full size image

Comparison of damage probability of near- and far-field

The similarity of damage probability can be presented by the evaluation of probability of failure in two major cities of Tehran and Tabriz in Iran, which are near the earthquake faults and located in a very high seismic zone. The seismic hazard curves of selected cities are shown in Fig. 7 (Ghofory Ashtiany and Nasserasadi 2010). To evaluate the collapse risk of selected frames, the exceeding probability of failure from different damage state were evaluated by Eq. 3 and shown in Table 7. No specific trend on the probability of failure of near- and far-field is observed, and the probability of failure of frames in near- and far-field earthquakes significantly differ in slight and extensive damage states, but is similar in moderate and close in complete damage state.

Fig. 7
figure 7

Hazard curves and fitted functions for city of Tehran and Tabriz

Full size image
Table 7 Probability of exceeding damage from different damage states in studied frames in near- and far-field of earthquake in selected cities
Full size table

Comparison of effect of number of story

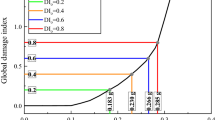
To study the effect of near-field earthquake on the two and three story frames separately, the fragility functions of two and three story frames in near- and far-field earthquakes were calculated and shown in the Figs. 8, 9, 10 and 11. Median and deviation of fragility functions are shown in Table 8. For comparison, the fragility function of HAZUS for low-rise concrete structure and its fragility parameters are shown in the Figs. 8, 9, 10 and 11 and Table 8 as well. In general, a good match between the calculated fragility and HAZUS fragility existed. The fragility of extensive and complete damage states are more close to HAZUS fragility function. From the figures, it can be observed that the fragility function of near-field and far-field in the slight and moderate damage states are very close, and in the extensive and complete damage states, the difference between near- and far-field fragility functions become more evident. This can be due to higher nonlinearity of structure in the extensive and complete damage state in which the behavior of structure becomes more sensitive to the ground motion type.

Fig. 8
figure 8

Comparison of the fragility curves of studied frames in near- and far-field of earthquake with fragility curve presented by HAZUS for slight damage state

Full size image
Fig. 9
figure 9

Comparison of fragility curves of 2-story frame in near- and far-field of earthquake with fragility curve presented by HAZUS for moderate damage state

Full size image
Fig. 10
figure 10

Comparison of fragility curves of studied frames in near- and far-field of earthquake with fragility curve presented by HAZUS for extensive damage state

Full size image
Fig. 11
figure 11

Comparison of fragility curves of studied frames in near- and far-field of earthquake with fragility curve presented by HAZUS for complete damage state

Full size image
Table 8 Numerical parameters of log-normal function fitted to amounts of fragility function in near- and far-field of earthquake
Full size table

A detailed examination of fragility function in two and three story frame demonstrates that median of fragility functions of two story frame in near-field earthquake is higher than the median of two story in far-field, suggesting the two story frame is more vulnerable in far-field. On the contrary, in the three story frame, the median of near-field is lower than the far-field, especially in extensive and collapse damage state, implying higher vulnerability of three story frame in near-field. These conflicting results can be justified by higher average value of response spectrum of far-field in period of two story frame (T = 0.53 s) and near-field in period of three story frame (T = 0.72 s) (see Fig. 3) that causes higher forces in the corresponding frames and make them more vulnerable resulting in lower median of fragility functions. This indicated that similar to regular earthquakes, the effect of near-field earthquakes strongly depends on the frequently contents of selected earthquakes which is projected in median of response spectrum.

Discussion and conclusions

In this paper, the probability of failure of low-rise concrete moment resistant frames designed according to the 3rd edition of Iranian seismic design code of practice for buildings design, were compared in near- and far-field earthquakes. For this purpose, two frames with two and three stories were considered and fragility function of structures was evaluated in the near- and far-field earthquakes. A mixture of pulse and non-pulse like records were selected for evaluation of fragility function of frames in the near-field earthquake. The probability of failure of frames in two different high seismic regions in Iran were evaluated and compared. In addition, fragility functions of two and three story frames are separately compared in near- and far-field earthquakes.

The results have shown that in general; the probability of failure of frames in near- and far-field is close, and no specific trend on the probability of failure of near- and far-filed can be observed. This result indicated that although it is believed that the structures in the near-field experiences more damages due to existing of pulses in ground motions, a realistic evaluation of the structural behavior in near-field earthquake does not support this assumption. In addition, the effect of near-field on the structural fragility of individual frames shows that, regardless of being in near- or far-field earthquakes, the frequency content of records is a more influential parameter. Therefore, in some cases, the effect of near-field is higher than far-field and in some other cases, the effect of far-field is higher than near-field.

The results of this study were evaluated based on limited study of low-rise concrete frame located in soil type I (rock or hard soil). To generalize the results, more and wide range of studies needs to be conducted in different structural height, soil type and seismic zones.