Wave propagation in cracked frame structures by the spectral element method

Abstract

This paper deals with the detection of crack in frame structures based on Euler–Bernoulli beams theorem by the Spectral Element Method. The effect of cracking is modeled using Castigliano’s theorem and laws of fracture mechanics as mass-less rotational and translational springs which are embedded in different locations of the steel frame structure in both beam and column. The crack location is revealed precisely without prior knowledge of their positions in frame structure. This means that there is no necessity to know the location and the node number which is assigned to crack. Finally the effect of crack when it is embedded simultaneously in both beam and column members, is also studied.

Introduction

Cracks in structures are a potential source of collapses in buildings especially at the time of earthquakes. Crack existence in column reduces the structural strength of the buildings and leads the whole structure to be in danger of failure. So this issue makes the damage detection such a prominent problem in civil engineering.

Wave propagation analysis is a good technique for damage detection with even if the small ones, but it also depends on the numerical method that will be derived for analyzing. Finite Element Method (FEM) has been used as a much more popular numerical method in comparison to other numerical methods such as boundary element method, transition matrix method and so on. This method is an open area of research yet, as Lee (2009) achieved to find multiple cracks using the vibration amplitudes by finite element method, it has been also found to be able detecting the crack locations accurately. In addition, Ovanesova and Suarez (2004) represented wavelet transformation using conventional finite element method. They used 50 finite elements for each beam–column member to obtain structural responses of damaged frames. But for impulsive loads with high frequency contents, using FEM is not effective, because it correspondingly needs to increase the number of elements to capture all the higher modes. So, it is necessary to use finer elements until the deformed solution converges to an accepted value. Hence, Doyle (1997) proposed a method in frequency domain as FFT-based Spectral Element Method (SEM) for solving this problem. In SEM the governing partial differential equations (PDE) are transferred to ordinary differential equations (ODE), next by Discrete Fourier Transform (DFT) the ODEs are all transformed into frequency domain. Finally, using Inverse Discrete Fourier Transform (IDFT) it is possible to obtain the responses into time domain. In this method the structures without any discontinuities can be modeled with just one element, and it is also possible to find displacements in any point of element without any extra nodes, so these advantageous have made this method unique in comparison to other numerical methods.

Palacz and Krawczuk (2002) represented wave propagation analysis for damage detection by Fourier Spectral Element Method (FSEM), where damage was modeled as non-propagating crack in rod and substituted by a dimensionless spring using Castigliano’s theorem. Then Krawczuk et al. (2006) determined the differences obtained by all the three other modified theories of rods plus to elementary one, and two different excited signals with high and low frequency contents have been used for finding damages in which they were similar to that of the aforementioned cracks. Krawczuk et al. (2003) developed this kind of cracks to that of the Timoshenko beam, they found this method more sufficient in comparison to other numerical methods for damage detection.

A delamination in beam as the other different kinds of damages has been also studied by Ostachowicz et al. (2004) by wave propagation analyses using SEM, but they asserted that for more sophisticated situations, it is just possible to show that there is damage, while determining the place of the damages lead to difficulty. That made it impossible to clearly discover the place of delaminations in beam. So they inevitably recommended using of genetic algorithm or neural networks for distinguishing the location and magnitude of a delamination in beam (Krawczuk and Ostachowicz 2002).

Gopalakrishnan et al. (2008) developed wave propagation in composite and inhomogeneous media by SEM, where different types of damage have been represented.

Prior researches just have involved give information about the crack locations in rods, beams and plates, but none has mentioned to the frame one. So this research aims to model crack by Castigliano’s theorem and laws of fracture mechanics in 2-D frame structures based on Euler–Bernoulli’s beam theorem using SEM. On the other hand the peak amounts of the incident waves throughout the elements have been traced to monitor the existence of likely damages in both beam and column. Eventually, the exact locations of the cracks with different damage rates monitored and then embedded simultaneously in both beam and column where their location in beam considered being constant while varying in the column element, to study the effects of the crack in displacement responses of the frame structure.

Local flexibility

To study about the structural health monitoring for detecting the potential likely crack-like damages, a suitable model of the crack is diagnosed important. So the Castigliano’s theorem is employed for a square cross-section beam–column element containing the transverse crack, where it is just included in the vertical plane. In this research work, beam–column elements are modeled by Euler–Bernoulli beams theorem, as it is expected that the shear deformations are not considered, so the crack is simulated by a translational and rotational springs, as shown in Fig. 1.

Fig. 1

Model of the cracked beam section with rotational and translational Springs

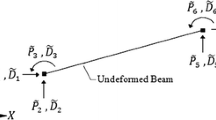
In the general case there are six nodal loads including the axial force, shearing forces, bending moments and also the torque. But in this specific case we only consider two independent nodal loading such as axial force and bending moment as shown in Fig. 2.

Fig. 2

Cracked beam–column element with axial force and bending moment

As aforementioned, flexibility at the crack location can be calculated using Castigliano’s theorem (Russell 2002) by the following expression:

$$C_{ij}=\frac{{\mathit{\partial }}^{2}U}{\mathit{\partial }{P}_i\mathit{\partial }{P}_j}i=1,2,j=1,2$$

(1)

where U denotes the elastic strain energy and P are the nodal loads.

$$U=\frac{1}{E}\underset{A}{\int }(K_{\mathrm{I},1}^2+K_{\mathrm{I},2}^2)\text{d}A$$

(2)

$K_{\mathrm{I},1}^2$ and $K_{\mathrm{I},2}^2$ are the stress intensity factors corresponding to the first mode of deformation of the crack in relation with the axial force and bending moment, respectively.

Axial flexibility

The stress intensity factor in relation with the axial force $P_1$ can be calculated as:

$$K_{\mathrm{I},1}=\frac{P_1}{A}\sqrt{\mathit{\pi }\mathit{\alpha }}{F}_1\left(\mathit{\alpha }/\phantom{\mathit{\alpha }b}b\right)$$

(3)

where $\mathit{\alpha }$ and $b$ are shown in Fig. 3.

Fig. 3

Cross-section of the beam–column element at crack location

And the correction function $F_1$ can be expressed as (Tada et al. 2000):

$$F_1\left(\mathit{\alpha }/\phantom{\mathit{\alpha }b}b\right)=\sqrt{\frac{2b}{\mathit{\pi }\mathit{\alpha }}tan\frac{\mathit{\pi }\mathit{\alpha }}{2b}}·\frac{0.752+2.02\left(\mathit{\alpha }/\phantom{\mathit{\alpha }b}b\right)+0.37{\left(1-sin\frac{\mathit{\pi }\mathit{\alpha }}{2b}\right)}^3}{cos\frac{\mathit{\pi }\mathit{\alpha }}{2b}}$$

(4)

$$\begin{array}{c}{C}_{\text{T}}=\frac{2\mathit{\pi }}{E{d}^2{b}^2}\underset{-\frac{d}{2}}{\overset{\frac{d}{2}}{\int }}\underset{0}{\overset{a}{\int }}\mathit{\alpha }{F}_1^2\left(\mathit{\alpha }/\phantom{\mathit{\alpha }b}b\right)\text{d}x\text{d}y=\frac{2\mathit{\pi }}{Ed{b}^2}\underset{0}{\overset{a}{\int }}\mathit{\alpha }{F}_1^2\left(\mathit{\alpha }/\phantom{\mathit{\alpha }b}b\right)\text{d}x\\ \overline{a}=\frac{a}{b},\overline{\mathit{\alpha }}=\frac{\mathit{\alpha }}{b}\to C_{\text{T}}=\frac{2\mathit{\pi }}{Ed}\underset{0}{\overset{\overline{a}}{\int }}\overline{\mathit{\alpha }}{F}_1^2\left(\overline{\mathit{\alpha }}\right)\text{d}\overline{\mathit{\alpha }}\\ \end{array}$$

(5)

$${\mathit{\theta }}_{\text{T}}=EA{C}_{\text{T}}$$

(6)

where $C_{\text{T}}$ is the axial flexibility due to the existence of the crack on the rod cross-section and ${\mathit{\theta }}_{\text{T}}$ is the dimensionless flexibility.

Bending flexibility

Similar to that of the axial flexibility, the stress intensity factor in relation with the bending moment $P_2$ can be also expressed as:

$$K_{\mathrm{I},2}=\frac{6P_2}{d{b}^2}\sqrt{\mathit{\pi }\mathit{\alpha }}{F}_2\left(\mathit{\alpha }/\phantom{\mathit{\alpha }b}b\right)$$

(7)

where $\mathit{\alpha }$, $b$ and $d$ are shown in Fig. 3.

$$F_2\left(\mathit{\alpha }/\phantom{\mathit{\alpha }b}b\right)=\sqrt{\frac{2b}{\mathit{\pi }\mathit{\alpha }}tan\frac{\mathit{\pi }\mathit{\alpha }}{2b}}\frac{0.923+0.199{\left(1-sin\frac{\mathit{\pi }\mathit{\alpha }}{2b}\right)}^4}{cos\frac{\mathit{\pi }\mathit{\alpha }}{2b}}$$

(8)

$$\begin{array}{c}{C}_{\text{R}}=\frac{72\mathit{\pi }}{E{d}^2{b}^4}\underset{-\frac{d}{2}}{\overset{\frac{d}{2}}{\int }}\underset{0}{\overset{a}{\int }}\mathit{\alpha }{F}_2^2\left(\mathit{\alpha }/\phantom{\mathit{\alpha }b}b\right)\text{d}x\text{d}y=\frac{72\mathit{\pi }}{Ed{b}^4}\underset{0}{\overset{a}{\int }}\mathit{\alpha }{F}_2^2\left(\mathit{\alpha }/\phantom{\mathit{\alpha }b}b\right)\text{d}x\\ \overline{a}=\frac{a}{b},\overline{\mathit{\alpha }}=\frac{\mathit{\alpha }}{b}\to C_{\text{R}}=\frac{72\mathit{\pi }}{Ed{b}^2}\underset{0}{\overset{\overline{a}}{\int }}\overline{\mathit{\alpha }}{F}_2^2\left(\overline{\mathit{\alpha }}\right)\text{d}\overline{\mathit{\alpha }}\\ \end{array}$$

(9)

$${\mathit{\theta }}_{\text{R}}=\frac{EI{C}_{\text{R}}}{L}$$

(10)

where $C_{\text{R}}$ is the bending flexibility due to the existence of the crack on the beam cross-section, L is the length of the element and ${\mathit{\theta }}_{\text{R}}$ is the dimensionless flexibility.

Rod spectral element

Rod spectral element method based on elementary rod theory with longitudinal displacement function $u(x)$, material characteristics: $\mathit{\rho }$ as volumetric density, E as Young modulus, and A as the cross-section area, where $k_{\text{r}}$ and ${\mathit{\omega }}_{\text{n}}$ are the rod’s wave number and natural frequency, respectively, is represented as (Doyle 1997):

$$u(x)=C_1^{\text{r}}{e}^{-i{k}_{\text{r}}x}+C_2^{\text{r}}{e}^{-i{k}_{\text{r}}(L-x)}$$

(11)

$$k_{\text{r}}={\mathit{\omega }}_{\text{n}}\sqrt{\frac{\mathit{\rho }A}{EA}}$$

(12)

where $C_1^{\text{r}}$ and $C_2^{\text{r}}$ are the forward and backward propagating wave amplitudes, respectively.

Rod spectral element with two finite elements

The solution is similar to Eq. (11) with the main difference that it is divided to the left and right part of the cracked rod, so by considering $u_1(x)$ and $u_2(x)$ as the spectral displacements for the left and right part of the rod, respectively, read:

$$\begin{array}{cc}{u}_1(x)=A_1^{\text{r}}{\text{e}}^{-i{k}_{\text{r}}x}+B_1^{\text{r}}{\text{e}}^{-i{k}_{\text{r}}(L_1-x)}& x\in (0,L_1)\\ u_2(x)=A_2^{\text{r}}{\text{e}}^{-i{k}_{\text{r}}(L_1+x)}+B_2^{\text{r}}{\text{e}}^{-i{k}_{\text{r}}(L_2-x)}& x\in (0,L_2)\end{array}$$

(13)

The crack is considered to be located at $L_1$ from the left part of the rod. So by assuming $L$ as the whole length of the rod, $L_2=L-L_1$.

The nodal spectral forces can be achieved by the relation between the axial forces and the displacement fields associated with the left part of the rod [$x=0$ for $u_1(x)$] and the right part of the rod [$x=L_2$ for $u_2(x)$]:

$$\begin{array}{c}{F}_a=EA\frac{\mathit{\partial }{u}_1(x=0)}{\mathit{\partial }x}\\ F_b=EA\frac{\mathit{\partial }{u}_2(x=L_2)}{\mathit{\partial }x}\\ \end{array}$$

(14)

Next, by considering the boundary conditions in association with the spectral displacements $u(x)$ for the left and right part of the cracked rod and the longitudinal dimensionless flexibility ${\mathit{\theta }}_{\text{L}}$ are as follows:

$$u_1(x=0)=q_1^{\text{r}}$$

(15)

$$\begin{array}{c}{u}_2(x=0)-u_1(x=L_1)={\mathit{\theta }}_{\text{L}}\frac{\mathit{\partial }{u}_1(x=L_1)}{\mathit{\partial }x}\\ \frac{\mathit{\partial }{u}_2(x=0)}{\mathit{\partial }x}=\frac{\mathit{\partial }{u}_1(x=L_1)}{\mathit{\partial }x}\\ \end{array}$$

(16)

$$u_2(x=L_2)=q_2^{\text{r}}$$

(17)

And then by taking into account the nodal spectral forces, we are able to obtain the dynamic stiffness in a matrix form as:

$$\left\{\begin{array}{c}{F}_a\\ F_b\end{array}\right\}=\left[F^{\text{r}}\right]\left\{\begin{array}{c}{A}_1^{\text{r}}\\ B_1^{\text{r}}\\ A_2^{\text{r}}\\ B_2^{\text{r}}\end{array}\right\}=\left[F^{\text{r}}\right]{\left[T^{\text{r}}\right]}^{-1}\left\{\begin{array}{c}{q}_1^{\text{r}}\\ 0\\ 0\\ q_2^{\text{r}}\end{array}\right\}\Rightarrow K_{\text{dyn}}=\left[F^{\text{r}}\right]{\left[T^{\text{r}}\right]}^{-1}$$

(18)

where $\left[F^{\text{r}}\right]$ and $\left[T^{\text{r}}\right]$ as the spectral force and displacement matrix for the rod spectral element, respectively are given in “Appendix”.

Euler–Bernoulli beam spectral element

Beam spectral element method with transverse displacement function $w(x)$, material characteristics: $\mathit{\rho }$ as volumetric density, E as Young modulus, I as geometrical moment of inertia and A as the cross-section area, where $k_{\text{b}}$ is the beam’s wave number, is represented as (Doyle 1997):

$$w(x)=C_1^{\text{b}}{\text{e}}^{-i{k}_{\text{b}}x}+C_2^{\text{b}}{\text{e}}^{-k_{\text{b}}x}+C_3^{\text{b}}{\text{e}}^{-i{k}_{\text{b}}(L-x)}+C_4^{\text{b}}{\text{e}}^{-k_{\text{b}}(L-x)}$$

(19)

$$k_{\text{b}}=\sqrt[4]{\frac{\mathit{\rho }A{\mathit{\omega }}^2}{EI}}i$$

(20)

where $C_1^{\text{b}},C_2^{\text{b}}$ and $C_3^{\text{b}},C_4^{\text{b}}$ are the forward and backward propagating wave amplitudes, respectively.

Beam spectral element with two finite elements

Similar to that of the rod spectral element with two finite elements, beam is also subdivided into two left and right parts of the cracked beam, where $w_1(x)$ and $w_2(x)$ are considered to be the transverse spectral displacements relevant to these two parts:

$$\begin{array}{cc}{w}_1(x)=A_1{\text{e}}^{-i{k}_{\text{b}}x}+B_1{\text{e}}^{-k_{\text{b}}x}+C_1{\text{e}}^{-i{k}_{\text{b}}(L_1-x)}+D_1{\text{e}}^{-k_{\text{b}}(L_1-x)}& x\in (0,L_1)\\ w_2(x)=A_2{\text{e}}^{-i{k}_{\text{b}}(x+L_1)}+B_2{\text{e}}^{-k_{\text{b}}(x+L_1)}+C_2{\text{e}}^{-i{k}_{\text{b}}(L_2-x)}+D_2{\text{e}}^{-k_{\text{b}}(L_2-x)}& x\in (0,L_2)\end{array}$$

(21)

In a similar manner, identical to the rod spectra element, we consider nodal spectral forces to the left and right parts of the element to that of the beam one. So here the nodal spectral forces included the shear and bending forces in relation to the transverse displacement field as follows:

$$V=EI\left(\frac{{\mathit{\partial }}^{3}w}{\mathit{\partial }{x}^3}\right)M=EI\left(\frac{{\mathit{\partial }}^{2}w}{\mathit{\partial }{x}^2}\right)$$

(22)

$$\begin{array}{c}{V}_1(x=0)=V_1{V}_2(x=L_2)=-V_2\\ M_1(x=0)=-M_1{M}_2(x=L_2)=M_2\\ \end{array}$$

(23)

The boundary conditions for the left and right parts of the beam spectral element with bending dimensionless flexibility ${\mathit{\theta }}_{\text{b}}$ can be considered as:

At the left end of the beam element:

$$w_1(x=0)=q_1^{\text{b}}\frac{\mathit{\partial }{w}_1(x=0)}{\mathit{\partial }x}=q_2^{\text{b}}$$

(24)

At the crack location:

$$\begin{array}{c}{w}_2(x=0)=w_1(x=L_1)\\ \frac{\mathit{\partial }{w}_2(x=0)}{\mathit{\partial }x}-\frac{\mathit{\partial }{w}_1(x=L_1)}{\mathit{\partial }x}={\mathit{\theta }}_{\text{b}}\frac{{\mathit{\partial }}^2{w}_1(x=L_1)}{\mathit{\partial }{x}^2}\\ \frac{{\mathit{\partial }}^2{w}_2(x=0)}{\mathit{\partial }{x}^2}=\frac{{\mathit{\partial }}^2{w}_1(x=L_1)}{\mathit{\partial }{x}^2}\\ \frac{{\mathit{\partial }}^3{w}_2(x=0)}{\mathit{\partial }{x}^3}=\frac{{\mathit{\partial }}^3{w}_1(x=L_1)}{\mathit{\partial }{x}^3}\\ \end{array}$$

(25)

At the right end of the beam element:

$$w_2(x=L_2)=q_3^{\text{b}}\frac{\mathit{\partial }{w}_2(x=L_2)}{\mathit{\partial }x}=q_4^{\text{b}}$$

(26)

Finally, by relating nodal spectral forces and boundary conditions, it is possible to obtain the dynamic stiffness in matrix form as follows:

$$\left\{\begin{array}{c}{V}_a\\ M_a\\ V_b\\ M_b\end{array}\right\}=\left[F^{\text{b}}\right]\left\{\begin{array}{c}{A}_1^{\text{b}}\\ B_1^{\text{b}}\\ C_1^{\text{b}}\\ D_1^{\text{b}}\\ A_2^{\text{b}}\\ B_2^{\text{b}}\\ C_2^{\text{b}}\\ D_2^{\text{b}}\end{array}\right\}=\left[F^{\text{b}}\right]{\left[T^{\text{b}}\right]}^{-1}\left\{\begin{array}{c}{q}_1^{\text{b}}\\ q_2^{\text{b}}\\ 0\\ 0\\ 0\\ 0\\ q_3^{\text{b}}\\ q_4^{\text{b}}\end{array}\right\}\Rightarrow K_{\text{dyn}}=\left[F^{\text{b}}\right]{\left[T^{\text{b}}\right]}^{-1}$$

(27)

where $\left[F^{\text{b}}\right]$ and $\left[T^{\text{b}}\right]$ as the spectral force and displacement matrix for that of the beam spectral element, respectively are given in “Appendix”.

Stiffness matrix of frame structures

The frame elements are composed by elementary rods in conjunction with Euler–Bernoulli beams which can be assembled in a way similar to conventional FEM.

The internal force and displacement matrix for each beam–column element can be represented as follows:

$$\left\{\begin{array}{c}{u}_1\\ w_1\\ {\mathit{\phi }}_1\\ u_2\\ w{}_2\\ {\mathit{\phi }}_2\end{array}\right\}=\left[\begin{array}{cccccc}1& 0& 0& {\text{e}}^{-i{k}_{\text{r}}L}& 0& 0\\ 0& 1& 1& 0& {\text{e}}^{-i{k}_{\text{b}}L}& {\text{e}}^{-k_{\text{b}}L}\\ 0& -i{k}_{\text{b}}& -k_{\text{b}}& 0& i{k}_{\text{b}}{\text{e}}^{-i{k}_{\text{b}}L}& k_{\text{b}}{\text{e}}^{-k_{\text{b}}L}\\ {\text{e}}^{-i{k}_{\text{r}}L}& 0& 0& 1& 0& 0\\ 0& {\text{e}}^{-i{k}_{\text{b}}L}& {\text{e}}^{-k_{\text{b}}L}& 0& 1& 1\\ 0& -i{k}_{\text{b}}{\text{e}}^{-i{k}_{\text{b}}L}& -k_{\text{b}}{\text{e}}^{-k_{\text{b}}L}& 0& i{k}_{\text{b}}& k_{\text{b}}\end{array}\right]\left\{\begin{array}{c}{A}_1^{\text{r}}\\ A_1^{\text{b}}\\ B_2^{\text{b}}\\ B_2^{\text{r}}\\ C_3^{\text{b}}\\ D_4^{\text{b}}\end{array}\right\}$$

(28)

$$\left\{\begin{array}{c}{P}_1\\ V_1\\ M_1\\ P_2\\ V_2\\ M_2\end{array}\right\}=\left[\begin{array}{cccccc}EAi{k}_{\text{r}}& 0& 0& -EAi{k}_{\text{r}}{\text{e}}^{-i{k}_{\text{r}}L}& 0& 0\\ 0& -EI{(i{k}_{\text{b}})}^3& -EI{(k_{\text{b}})}^3& 0& EI{(i{k}_{\text{b}})}^3{\text{e}}^{-i{k}_{\text{b}}L}& EI{(k_{\text{b}})}^3{\text{e}}^{-k_{\text{b}}L}\\ 0& -EI{(i{k}_{\text{b}})}^2& -EI{(k_{\text{b}})}^2& 0& -EI{(i{k}_{\text{b}})}^2{\text{e}}^{-i{k}_{\text{b}}L}& -EI{(k_{\text{b}})}^2{\text{e}}^{-k_{\text{b}}L}\\ -EAi{k}_{\text{r}}{\text{e}}^{-i{k}_{\text{r}}L}& 0& 0& EAi{k}_{\text{r}}& 0& 0\\ 0& EI{(i{k}_{\text{b}})}^3{\text{e}}^{-i{k}_{\text{b}}L}& EI{(k_{\text{b}})}^3{\text{e}}^{-k_{\text{b}}L}& 0& -EI{(i{k}_{\text{b}})}^3& -EI{(k_{\text{b}})}^3\\ 0& EI{(i{k}_{\text{b}})}^2{\text{e}}^{-i{k}_{\text{b}}L}& EI{(k_{\text{b}})}^2{\text{e}}^{-k_{\text{b}}L}& 0& EI{(i{k}_{\text{b}})}^2& EI{(k_{\text{b}})}^2\end{array}\right]\left\{\begin{array}{c}{A}_1^{\text{r}}\\ A_1^{\text{b}}\\ B_2^{\text{b}}\\ B_2^{\text{r}}\\ C_3^{\text{b}}\\ D_4^{\text{b}}\end{array}\right\}$$

(29)

By relating internal forces and the nodal displacements in a matrix form, it is possible to obtain the stiffness matrix of the frame structure.

$$\begin{array}{c}\{\widehat{F}\}=[\widehat{K}]\{\widehat{U}\}\\ {[\widehat{K}]}_{12\times 12}={[R]}^{\text{T}}[\overline{K}][R]\\ \end{array}$$

(30)

$$R=\left[\begin{array}{cccccc}cos\mathit{\alpha }& sin\mathit{\alpha }& 0& 0& 0& 0\\ -sin\mathit{\alpha }& cos\mathit{\alpha }& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0\\ 0& 0& 0& cos\mathit{\alpha }& sin\mathit{\alpha }& 0\\ 0& 0& 0& -sin\mathit{\alpha }& cos\mathit{\alpha }& 0\\ 0& 0& 0& 0& 0& 1\end{array}\right]$$

(31)

where $[\widehat{K}]$ is the $12\times 12$ complex matrix for one-bay frame structure, and $[R]$ is the rotation matrix to transform the local stiffness matrix of the beam–column members to that of the global one.

Numerical examples

Here the ability of the SEM in crack detection in one-bay portal frame is demonstrated. The material characteristics and the dimensions of the beam and column members of the frame structure which is subjected to sinusoid impulsive load are shown in Table 1. This impulsive load is diagnosed to be in form of the sine wave which is modulated with Hanning window to avoid leakage errors (de Silva 2007). So it has been seen suitable to use signals which last for short period of time and correspondingly containing wider range of frequency, hence it is used of signal with 170 KHZ excited frequency, as shown in Fig. 4.

Table 1 Details of the steel frame structure

Fig. 4

Time history of impulsive load (a) and its FFT (b)

To make it possible to diagnose the place of crack in frame structure in both beam and column members we used the differences between signals obtained from undamaged and damaged frame. The crack depth which is embedded in beam member varying from 3 to 5 % of the height of the beam with an increment of 1 % is as opposed to 5 % of the height of the column for column member.

Figure 6a shows the vertical displacement response of the frame structure where the impulsive load is applied in a vertical position as shown in Fig. 5b. Figure. 6b shows the horizontal displacement response of the frame structure where the impulsive load is applied in a horizontal position as shown in Fig. 5a. These responses are measured at the place where the impulsive load is applied.

Fig. 5

One-bay steel frame under impulsive loads applied in a horizontal (a) and vertical (b) positions

Fig. 6

Vertical (a) and horizontal (b) displacement responses at the place where the impulsive load is applied

Figure 7 shows the differences between signals obtained from damaged and undamaged frame structure where damage is embedded in the beam element, the crack depth varying from 3 to 5 % with an increment of 1 %. Since, in displacement responses obtained from cracked structure it is not specifically able to distinguish the changes by embedding crack, hence inevitably we avoided representing them here for brevity and we have just represented their differences in relation to the undamaged structure responses. As it is obvious from Fig. 7, when we declined the crack depth, the amplitude of differences between responses obtained from damaged and undamaged frame structure as expected, decreased. Reflected signals from crack place are obviously shown in Figs. 7, 8 and 9, the other additional signals are because of existence of crack in structure which makes it difficult to diagnose the place where crack is embedded. So to recognize which reflected signal would be the desired one, to help us to find damage place, crack in different places of the beam member has been embedded and the additional signal in which it is reflected from crack place is also demonstrated in Fig. 8.

Fig. 7

Differences between horizontal displacement of damaged and undamaged frame with crack depth equal to 5 % (a), 4 % (b) and 3 % (c), embedded in beam and located at 0.5 m

Fig. 8

Differences between horizontal displacement of damaged and undamaged frame with crack depth equal to 5 %, embedded in beam and located at 1 m (a) and 1.5 m (b)

Fig. 9

Difference between vertical displacement of damaged and undamaged frame with crack depth equal to 5 %, embedded in column

In Fig. 9 the ability of the method also in finding damage in the column member are presented. In this figure the difference between displacement response of the damaged and undamaged frame structure where crack is located at 3.5 m away from clamping support with crack depth equal to 5 % is demonstrated.

On the other part, the location of the crack in relation to the position of the beam member is shown in Fig. 10. As aforementioned, one of the most prominent features of the SEM is its ability to demonstrate all the responses of the structures without introducing any extra node. So, using this point and measuring the longitudinal responses in different positions of the frame structure and extracting the peak amplitude of the incident waves, it is possible to recognize the exact place of the crack in both beam and column members. In Fig. 10a, fluctuations which are emerged from latter half of the beam member are because of reflected waves, which make it a little bit difficult to distinguish the likely damages that are occurred in these regions. So, to relieve from this problem it is suggested monitoring the latter half of the beam member also from the opposite side. In Fig. 10b where the crack is embedded at 3.5 m away from clamping support, such a problem is not observed. At distance 4 m away from the place where the impulsive load is applied, there is clamping support in which all the responses indeed should be zero, as this figure also approves this.

Fig. 10

Crack location in beam (a) and column (b)

Figure 11 represents the horizontal displacement responses of the frame structure when crack is embedded simultaneously in both beam and column. The place of the crack in beam is considered to be constant, equal to 0.5 m, while in the left column it changed from 0.2 to 1 m and the right column is assumed to be intact.

Fig. 11

Differences between horizontal displacement of damaged and undamaged frame where crack is located at 0.5 m from end left of beam, and is also embedded at 3.8 m (a) and 3 m (b) away from clamping support of column

At the time when crack embedded simultaneously in both beam and column and horizontal responses of the frame structure has been measured, other additional reflected signals because of existence of crack are also emerged.

By considering the case where the crack location is constant in beam element and it differs from 0.2 to 1 m in column, it is concluded that because of existence of crack, also in column, another wave which is assigned as wave C, as is shown in Fig. 11, emerged and except its amplitude, its place associated with time did not differ by changing the place of crack in column. But wave B which is appeared because of existence of crack in beam, neither the place nor the amplitude changed.

By increasing the distance of crack from the place where the impulsive load is applied, it has been demonstrated that wave A which was emerged because of existence of crack in column, took longer time to be revealed. So it can be a good indicator to diagnose the place of the crack in column.

Conclusions

A frame structure composed by Euler beams has been stimulated under an impulsive load for finding crack in different locations of the steel structure in both beam and column. So the signal propagated through out the damaged frame structure in which the crack-like damage has been modeled as a localized flexibility using Castigliano’s theorem and laws of fracture mechanics.

In this research work, first the effects of the different depths of the crack have been shown, to demonstrate the ability of the method in finding damages precisely, with even if the least amounts of failures. Then the existence of crack, in both beam and column, separately represented. And the ability of the method in displaying the crack place in relation to the position of the relevant members is shown successfully.

Finally by applying crack simultaneously in both in beam and column, where hitherto no one has mentioned to this issue neither by SEM nor conventional FEM, the effects of the crack in both members which has changed the horizontal displacement responses of the frame in comparison to that of the case where the crack has only been embedded in beam member, is also studied.

In this research work, it is shown that damage in different places of the frame structure is possible to be obtained, in other word, it is not limited to the specific places of the structure. On the other hand, it is not mentioned to the likely damages which can be occurred at the base of the frame structure or in the beam–column connections, where additional research works can be extended to.

Appendix

• Spectral force matrix for the rod spectral element:

  $$\left[F^{\text{r}}\right]=EA\left[\begin{array}{cccc}i{k}_{\text{r}}& -i{k}_{\text{r}}{\text{e}}^{-i{k}_{\text{r}}{L}_1}& 0& 0\\ 0& 0& -i{k}_{\text{r}}{\text{e}}^{-i{k}_{\text{r}}(L_1+L_2)}& i{k}_{\text{r}}\end{array}\right]$$

  (32)

• Spectral displacement matrix for the rod spectral element:

  $$\left[T^{\text{r}}\right]=\left[\begin{array}{cccc}1& {\text{e}}^{-i{k}_{\text{r}}{L}_1}& 0& 0\\ -{\text{e}}^{-i{k}_{\text{r}}{L}_1}(1-{\mathit{\theta }}_{\text{L}}i{k}_{\text{r}})& -1-{\mathit{\theta }}_{\text{L}}i{k}_{\text{r}}& {\text{e}}^{-i{k}_{\text{r}}{L}_1}& {\text{e}}^{-i{k}_{\text{r}}{L}_2}\\ -i{k}_{\text{r}}{\text{e}}^{-i{k}_{\text{r}}{L}_1}& i{k}_{\text{r}}& i{k}_{\text{r}}{\text{e}}^{-i{k}_{\text{r}}{L}_1}& -i{k}_{\text{r}}{\text{e}}^{-i{k}_{\text{r}}{L}_2}\\ 0& 0& {\text{e}}^{-i{k}_{\text{r}}(L_1+L_2)}& 1\end{array}\right]$$

  (33)

• Spectral force matrix for the beam spectral element:

  $$\left[F^{\text{b}}\right]=EI\left[\begin{array}{cccccccc}{(-i{k}_{\text{b}})}^3& {(-k_{\text{b}})}^3& {(i{k}_{\text{b}})}^3{\text{e}}^{-i{k}_{\text{b}}{L}_1}& {(k_{\text{b}})}^3{\text{e}}^{-k_{\text{b}}{L}_1}& 0& 0& 0& 0\\ -{(i{k}_{\text{b}})}^2& -{(k_{\text{b}})}^2& -{(i{k}_{\text{b}})}^2{\text{e}}^{-i{k}_{\text{b}}{L}_1}& -{(k_{\text{b}})}^2{\text{e}}^{-k_{\text{b}}{L}_1}& 0& 0& 0& 0\\ 0& 0& 0& 0& -{(-i{k}_{\text{b}})}^3{\text{e}}^{-i{k}_{\text{b}}(L_2+L_1)}& -{(-k_{\text{b}})}^3{\text{e}}^{-k_{\text{b}}(L_2+L_1)}& -{(i{k}_{\text{b}})}^3& -{(k_{\text{b}})}^3\\ 0& 0& 0& 0& {(i{k}_{\text{b}})}^2{\text{e}}^{-i{k}_{\text{b}}(L_2+L_1)}& {(k_{\text{b}})}^2{\text{e}}^{-k_{\text{b}}(L_2+L_1)}& {(i{k}_{\text{b}})}^2& {(k_{\text{b}})}^2\end{array}\right]$$

  (34)

• Spectral displacement matrix for the beam spectral element:

  $$\left[T^{\text{b}}\right]=\left[\begin{array}{cccccccc}1& 1& {\text{e}}^{-i{k}_{\text{b}}{L}_1}& {\text{e}}^{-k_{\text{b}}{L}_1}& 0& 0& 0& 0\\ -i{k}_{\text{b}}& -k_{\text{b}}& i{k}_{\text{b}}{\text{e}}^{-i{k}_{\text{b}}{L}_1}& k_{\text{b}}{\text{e}}^{-k_{\text{b}}{L}_1}& 0& 0& 0& 0\\ -{\text{e}}^{-i{k}_{\text{b}}{L}_1}& -{\text{e}}^{-k_{\text{b}}{L}_1}& -1& -1& {\text{e}}^{-i{k}_{\text{b}}{L}_1}& {\text{e}}^{-k_{\text{b}}{L}_1}& {\text{e}}^{-i{k}_{\text{b}}{L}_2}& {\text{e}}^{-k_{\text{b}}{L}_2}\\ i{k}_{\text{b}}{\text{e}}^{-i{k}_{\text{b}}{L}_1}(1-{\mathit{\theta }}_{\text{b}}(i{k}_{\text{b}}))& k_{\text{b}}{\text{e}}^{-k_{\text{b}}{L}_1}(1-{\mathit{\theta }}_{\text{b}}{k}_{\text{b}})& i{k}_{\text{b}}(-1-{\mathit{\theta }}_{\text{b}}(i{k}_{\text{b}}))& k_{\text{b}}(-1-{\mathit{\theta }}_{\text{b}}(k_{\text{b}}))& -i{k}_{\text{b}}{\text{e}}^{-i{k}_{\text{b}}{L}_1}& -k_{\text{b}}{\text{e}}^{-k_{\text{b}}{L}_1}& i{k}_{\text{b}}{\text{e}}^{-i{k}_{\text{b}}{L}_2}& k_{\text{b}}{\text{e}}^{-k_{\text{b}}{L}_2}\\ -{(i{k}_{\text{b}})}^2{\text{e}}^{-i{k}_{\text{b}}{L}_1}& -{(k_{\text{b}})}^2{\text{e}}^{-k_{\text{b}}{L}_1}& -{(i{k}_{\text{b}})}^2& -{(k_{\text{b}})}^2& {(i{k}_{\text{b}})}^2{\text{e}}^{-i{k}_{\text{b}}{L}_1}& {(k_{\text{b}})}^2{\text{e}}^{-k_{\text{b}}{L}_1}& {(i{k}_{\text{b}})}^2{\text{e}}^{-i{k}_{\text{b}}{L}_2}& {(k_{\text{b}})}^2{\text{e}}^{-k_{\text{b}}{L}_2}\\ -{(-i{k}_{\text{b}})}^3{\text{e}}^{-i{k}_{\text{b}}{L}_1}& -{(-k_{\text{b}})}^3{\text{e}}^{-k_{\text{b}}{L}_1}& -{(i{k}_{\text{b}})}^3& -{(k_{\text{b}})}^3& {(-i{k}_{\text{b}})}^3{\text{e}}^{-i{k}_{\text{b}}{L}_1}& {(-k_{\text{b}})}^3{\text{e}}^{-k_{\text{b}}{L}_1}& {(i{k}_{\text{b}})}^3{\text{e}}^{-i{k}_{\text{b}}{L}_2}& {(k_{\text{b}})}^3{\text{e}}^{-k_{\text{b}}{L}_2}\\ 0& 0& 0& 0& {\text{e}}^{-i{k}_{\text{b}}(L_2+L_1)}& {\text{e}}^{-k_{\text{b}}(L_2+L_1)}& 1& 1\\ 0& 0& 0& 0& -i{k}_{\text{b}}{\text{e}}^{-i{k}_{\text{b}}(L_2+L_1)}& -k_{\text{b}}{\text{e}}^{-k_{\text{b}}(L_2+L_1)}& i{k}_{\text{b}}& k_{\text{b}}\end{array}\right]$$

  (35)