On the determination of a developable spherical orthotomic ruled surface

Abstract

In this paper, a method for determination of developable spherical orthotomic ruled surfaces is given by using dual vector calculus. We show that dual vectorial expression of a developable spherical orthotomic ruled surface can be obtained from coordinates and the first derivatives of the base curve. The paper concludes with an example related to this method.

1 Introduction

In geometry, a surface is called a ruled surface if it is swept out by a moving line in $\mathbb {R}^{3}$. The theory of ruled surfaces is a classical subject in differential geometry. It is well known that developable surfaces are special cases of ruled surfaces [18]. Developable surfaces have a very important place in mathematics and engineering such as motion analysis or designing cars and ships.

Let $\alpha$ be a regular curve and $\overrightarrow{T}$ be its tangent, and let $u$ be a source. An orthotomic of $\alpha$ with respect to the source ($u$) is defined as a locus of reflection of $u$ about tangents $\overrightarrow{T}$ [8]. Bruce and Giblin applied the unfolding theory to the study of the evolutes and orthotomics of plane and space curves [3–5]. Georgiou, Hasanis and Koutroufiotis investigated the orthotomics in the Euclidean (n $+$ 1) space [7]. Alamo and Criado studied the antiorthotomics in the Euclidean (n $+$ 1)-space [1]. Xiong defined the spherical orthotomic and the spherical antiorthotomic [20]. Also, an orthotomic concept can be applied to surface. For a given surface $S$ and a fixed point (source) $P$, orthotomic surface of $S$ relative to $P$ is defined as a locus of reflection of $P$ about all tangent planes of $S$ [11].

Dual numbers were defined by Clifford (1873) with the aid of real numbers. After him E. Study has done fundamental research with dual numbers and dual vectors on the geometry of lines and kinematics [2] introducing what is now called the Study mapping. This mapping constitutes a one-to-one correspondence between the dual points of dual unit sphere $S^{2}$ and the directed lines of space of lines $\mathbb {R}^{3}$ [19]. Therefore, the motion locus of a straight line in $\mathbb {R}^{3}$ can be identified by a point on the source of dual unit sphere $S^{2}$ in $\mathbb { D}$ Module $\mathbb {D}^{3}$. Afterwards Guggenheimer studied relationship between a ruled surface in $\mathbb {R}^{3}$ and unique dual curve on the surface of $S^{2}$ [9].

Köse introduced a method for determination of developable ruled surfaces [13]. In this study, by using methods given [13], we construct a method for determination of developable orthotomic ruled surfaces and obtain a linear differential equation of first order.

2 Preliminaries

If $a$ and $a^{*}$ are real numbers and $\varepsilon ^{2}=0$ with $\varepsilon \notin \mathbb {R}$, a dual number can be written as $\widehat{a} =a+\varepsilon a^{*},$ where $\varepsilon =(0,1)$ is the dual unit.

The set $\left\{ \widehat{a}=a+\varepsilon a^{*}\left| a,a^{*}\in \mathbb {R}\right. \right\}$ of dual numbers forms a commutative ring over $\mathbb {R}$ and is denoted by $\mathbb {D}$. Then the set

$$\begin{aligned} \mathbb {D}^{3}=\left\{ \overrightarrow{\widehat{a}}=(\widehat{a}_{1}, \widehat{a}_{2},\widehat{a}_{3})\left| \widehat{a}_{i}\in \mathbb {D},1\le i\le 3\right. \right\} \end{aligned}$$

becomes a module over the ring $\mathbb {D}$ which is called $\mathbb {D}$ Module, under addition and scalar multiplication on $\mathbb {D}$ [14]. The elements of $\mathbb {D}^{3}$ are called dual vectors. Thus, a dual vector has the form $\overrightarrow{\widehat{a}}=\overrightarrow{a} +\varepsilon \overrightarrow{a}^{*},$ where $\overrightarrow{a}$ and $\overrightarrow{a}^{*}$ are real vectors in $\mathbb {R}^{3}$. For any vectors $\overrightarrow{\widehat{a}}$ and $\overrightarrow{\widehat{b}}$ in $\mathbb {D}^{3},$ the inner product and the vector product of these vectors are defined as

$$\begin{aligned} \left\langle \overrightarrow{\widehat{a}},\overrightarrow{\widehat{b}} \right\rangle =\left\langle \overrightarrow{a},\overrightarrow{b} \right\rangle +\varepsilon \left( \left\langle \overrightarrow{a}, \overrightarrow{b}^{*}\right\rangle +\left\langle \overrightarrow{a} ^{*},\overrightarrow{b}\right\rangle \right) \end{aligned}$$

and

$$\begin{aligned} \overrightarrow{\widehat{a}}\wedge \overrightarrow{\widehat{b}}= \overrightarrow{a}\wedge \overrightarrow{b}+\varepsilon \left( \overrightarrow{a}\wedge \overrightarrow{b}^{*}+\overrightarrow{a}^{*}\wedge \overrightarrow{b}\right) , \end{aligned}$$

respectively. The norm $\left\| \overrightarrow{\widehat{a}}\right\|$ of $\overrightarrow{\widehat{a}}=\overrightarrow{a}+\varepsilon \overrightarrow{a}^{*}$ is defined as

$$\begin{aligned} \left\| \overrightarrow{\widehat{a}}\right\| =\left\| \overrightarrow{a}\right\| +\varepsilon \frac{\left\langle \overrightarrow{a},\overrightarrow{a}^{*}\right\rangle }{\left\| \overrightarrow{a}\right\| },\overrightarrow{a}\ne 0. \end{aligned}$$

The dual vector $\overrightarrow{\widehat{a}}$ with norm $1$ is called a dual unit vector. The set of dual unit vectors

$$\begin{aligned} \widehat{S}^{2}=\left\{ \overrightarrow{\widehat{a}}=\overrightarrow{a} +\varepsilon \overrightarrow{a}^{*}\in \mathbb {D}^{3}\left| \left\| \overrightarrow{\widehat{a}}\right\| =1;\overrightarrow{a },\overrightarrow{a}^{*}\in \mathbb {R}^{3}\right. \right\} \end{aligned}$$

is called the dual unit sphere.

Theorem 1

The Study Mapping is a one-to-one mapping between the dual points of a dual unit sphere, in $\mathbb {D}$ Module, and the oriented lines in the Euclidean line space $\mathbb {E}^{3}$ [10]$.$

According to Theorem 1, the unit dual vector $\overrightarrow{\widehat{a}}= \overrightarrow{a}+\varepsilon \overrightarrow{a}^{*}$ corresponds to only oriented line; where the real vector $\overrightarrow{a}$ shows the direction of this line and the real vector $\overrightarrow{a}^{*}$ shows the vectorial moment of the unit vector $\overrightarrow{a}$ with respect to the origin point.

Let $\widehat{S}^{2},O$ and $\left\{ O;\overrightarrow{\widehat{e}}_{1}, \overrightarrow{\widehat{e}}_{2},\overrightarrow{\widehat{e}}_{3}\right\}$ denote the unit dual sphere, the center of $\widehat{S}^{2}$ and dual orthonormal system at $O$, respectively, where

$$\begin{aligned} \overrightarrow{\widehat{e}}_{i}=\overrightarrow{e}_{i}+\varepsilon \overrightarrow{e}_{i}^{*};\quad 1\le i\le 3. \end{aligned}$$

Let $S_{3}$ be the group of permutations of $\left\{ 1,2,3\right\} ,$ then it can be written as

$$\begin{aligned} \left. \begin{array}{c} \overrightarrow{\widehat{e}}_{\sigma (1)}=\mathrm{sgn}(\sigma )\overrightarrow{ \widehat{e}}_{\sigma (2)}\wedge \overrightarrow{\widehat{e}}_{\sigma (3)},\mathrm{sgn}(\sigma )=\pm 1, \\ \sigma =\left( \begin{array}{ccc} 1 &{} 2 &{} 3 \\ \sigma (1) &{} \sigma (2) &{} \sigma (3) \end{array} \right) \end{array} \right\} . \end{aligned}$$

In the case that the orthonormal system

$$\begin{aligned} \left\{ O;\overrightarrow{e}_{1},\overrightarrow{e}_{2},\overrightarrow{e} _{3}\right\} \end{aligned}$$

is the system of $\mathbb {E}^{3}$.

By using the Study Mapping, we can conclude that there exists a one-to-one correpondence between the dual orthonormal system and the real orthonormal system.

Now, define of spherical normal, spherical tangent and spherical orthotomic of a spherical curve $\alpha$. Let $\left\{ \overrightarrow{T}, \overrightarrow{N},\overrightarrow{B}\right\}$ be the Frenet frame of $\alpha$. The spherical normal of $\alpha$ is the great circle, passing through $\alpha (s),$ that is normal to $\alpha$ at $\alpha (s)$ and given by

$$\begin{aligned} \left\{ \begin{array}{c} \left\langle \overrightarrow{x},\overrightarrow{x}\right\rangle =1, \\ \left\langle \overrightarrow{x},\overrightarrow{T}\right\rangle =0, \end{array} \right. \end{aligned}$$

where $x$ is an arbitrary point of the spherical normal. The spherical tangent of $\alpha$ is the great circle which tangent to $\alpha$ at $\alpha (s)$ and given by

$$\begin{aligned} \left\{ \begin{array}{l} \left\langle \overrightarrow{y},\overrightarrow{y}\right\rangle =1, \\ \left\langle \overrightarrow{y},(\overrightarrow{\alpha }\wedge \overrightarrow{T})\right\rangle =0, \end{array} \right. \end{aligned}$$

(2.1)

where $y$ is an arbitrary point of the spherical tangent.

Let $u$ be a source on a sphere. Then, Xiong defined the spherical orthotomic of $\alpha$ relative to $u$ as to be the set of reflections of $u$ about the planes, lying on the above great circles (2.1) for all $s\in I$ and given by

$$\begin{aligned} \overrightarrow{\widetilde{u}}=2\left\langle \left( \overrightarrow{\alpha } -\overrightarrow{u}\right) ,\overrightarrow{v}\right\rangle \overrightarrow{ v}+\overrightarrow{u} \end{aligned}$$

(2.2)

where $\overrightarrow{v}=\frac{\overrightarrow{B}-\left\langle \overrightarrow{B},\overrightarrow{\alpha }\right\rangle \overrightarrow{ \alpha }}{\left\| \overrightarrow{B}-\left\langle \overrightarrow{B}, \overrightarrow{\alpha }\right\rangle \overrightarrow{\alpha }\right\| }$ [21].

3 The dual vector formulation

Let $L$ be a line and $x$ denotes the direction and $p$ be the position vector of any point on $L$. Dual vector representation allows us the Plucker vectors $x$ and $p\wedge x$. Thus, dual vector $\widehat{x}(t)$ can be written as

$$\begin{aligned} \widehat{x}(t)=x+\varepsilon (p\wedge x)=x+\varepsilon x^{*} \end{aligned}$$

where $\varepsilon$ is called the dual unit and $\varepsilon ^{2}=0$.

By using the dual vector function $\widehat{x}(t)=x(t)+\varepsilon (p(t)\wedge x(t))=x(t)+\varepsilon x^{*}(t)$, a ruled surface can be given as

$$\begin{aligned} m(u,t)=p(t)+ux(t). \end{aligned}$$

It is known that the dual unit vector $\widehat{x}(t)$ is a differentiable curve on a dual unit sphere and also having unit magnitude [15]:

$$\begin{aligned} \left\langle \widehat{x},\widehat{x}\right\rangle&= \left\langle x+\varepsilon p\wedge x,x+\varepsilon p\wedge x\right\rangle \\&= \left\langle x,x\right\rangle +\left\langle 2\varepsilon x,p\wedge x\right\rangle +\varepsilon ^{2}\left\langle p\wedge x,p\wedge x\right\rangle \\&= \left\langle x,x\right\rangle \\&= 1. \end{aligned}$$

The dual arc-length of the ruled surface $\widehat{x}(t)$ is defined by

$$\begin{aligned} \hat{s}\left( t \right) = \int \limits _0^t {\left\| {\frac{{d\hat{x}}}{{dt}}} \right\| } dt. \end{aligned}$$

(3.1)

The integrant of the Eq. (3.1) is the dual speed $\widehat{\delta }$ of $\widehat{x}(t)$ and is

$$\begin{aligned} \widehat{\delta }=\left\| \frac{d\widehat{x}}{dt}\right\| =\left\| \frac{dx}{dt}\right\| \left( 1+\varepsilon \frac{\left\langle \frac{dx}{dt},\frac{dp}{dt}\wedge x\right\rangle }{\left\| \frac{dx}{dt} \right\| ^{2}}\right) =\left\| \frac{dx}{dt}\right\| (1+\varepsilon \Delta ). \end{aligned}$$

The curvature function

$$\begin{aligned} \Delta =\frac{\left\langle \frac{dx}{dt},\frac{dp}{dt}\wedge x\right\rangle }{\left\| \frac{dx}{dt}\right\| ^{2}}=\frac{\left\langle \frac{dx}{dt},\frac{dx^{*}}{dt}\right\rangle }{\left\| \frac{dx}{dt} \right\| ^{2}} \end{aligned}$$

(3.2)

is the well-known distribution parameter (drall) of the ruled surface.

4 The determination of a developable ruled surface

Let $\widehat{x}(t)$ be a point on the dual unit sphere. The dual coordinates of $\widehat{x}(t)=x_{i}+\varepsilon x_{i}^{*}$ can be expressed as

$$\begin{aligned} \widehat{x}_{1}&= x_{1}+\varepsilon x_{1}^{*}=\cos \widehat{\varphi } \sin \widehat{\theta } \nonumber \\ \widehat{x}_{2}&= x_{2}+\varepsilon x_{2}^{*}=\sin \widehat{\varphi } \sin \widehat{\theta } \\ \widehat{x}_{3}&= x_{3}+\varepsilon x_{3}^{*}=\cos \widehat{\theta } \nonumber \end{aligned}$$

(4.1)

where $\widehat{\varphi }=\varphi +\varepsilon \varphi ^{*},$$\widehat{ \theta }=\theta +\varepsilon \theta ^{*}$ are dual angles.

Since $\varepsilon ^{2}=\varepsilon ^{3}=\cdots =0$ according to the Taylor series expansion from (4.1), we obtain the real parts as

$$\begin{aligned} x_{1}&= \cos \varphi \sin \theta , \\ x_{2}&= \sin \varphi \sin \theta , \\ x_{3}&= \cos \theta , \end{aligned}$$

and the dual parts as

$$\begin{aligned} x_{1}^{*}&= \theta ^{*}\cos \varphi \cos \theta -\varphi ^{*}\sin \varphi \sin \theta \\ x_{2}^{*}&= \theta ^{*}\sin \varphi \cos \theta +\varphi ^{*}\cos \varphi \sin \theta \\ x_{3}^{*}&= -\theta ^{*}\sin \theta . \end{aligned}$$

Hence, we conclude that a dual curve $\widehat{x}(t)=x(t)+\varepsilon x^{*}(t)$ can be written as

$$\begin{aligned} \widehat{x}(t)&= \left( \cos \varphi (t)\sin \theta (t),\sin \varphi (t)\sin \theta (t),\cos \theta (t)\right) \\&+\varepsilon \left( \begin{array}{c} \theta ^{*}(t)\cos \varphi (t)\cos \theta (t)-\varphi ^{*}(t)\sin \varphi (t)\sin \theta (t), \\ \theta ^{*}(t)\sin \varphi (t)\cos \theta (t)+\varphi ^{*}(t)\cos \varphi (t)\sin \theta (t),-\theta ^{*}(t)\sin \theta (t) \end{array} \right) . \end{aligned}$$

Let $\widehat{\sigma }(t)={\sigma }(t)+\varepsilon {\sigma }^{*}(t)$ be spherical orthotomic of the great circle, which lies on the $\overrightarrow{ \widehat{e}}_{2}\overrightarrow{\widehat{e}}_{3}$ plane, relative to the dual curve $\widehat{x}(t)$. By (2.2), we get $\widehat{\sigma }(t)=\left( -\widehat{x}_{1},\widehat{x}_{2},\widehat{x} _{3}\right)$ where $\widehat{x}_{i}$’s are the coordinates of $\widehat{x} (t)$ for $i=1,2,3.$ By considering the spherical orthotomic dual curve, we have:

$$\begin{aligned} \widehat{\sigma }(t)&= \left( -\cos \varphi (t)\sin \theta (t),\sin \varphi (t)\sin \theta (t),\cos \theta (t)\right) \\&+\varepsilon \left( \begin{array}{c} -\theta ^{*}(t)\cos \varphi (t)\cos \theta (t)+\varphi ^{*}(t)\sin \varphi (t)\sin \theta (t), \\ \theta ^{*}(t)\sin \varphi (t)\cos \theta (t)+\varphi ^{*}(t)\cos \varphi (t)\sin \theta (t),-\theta ^{*}(t)\sin \theta (t) \end{array} \right) \end{aligned}$$

on the dual unit sphere corresponding to ruled surface

$$\begin{aligned} m(u,t)=q(t)+u\sigma (t), \end{aligned}$$

where $q(t)$ is a base curve of the ruled surface. Since $\sigma ^{*}(t)=$$q(t)\wedge \sigma (t),$ we have the following system of linear equations in variables$Q_{1},Q_{2},Q_{3}$;

$$\begin{aligned} Q_{2}\cos \theta -Q_{3}\sin \varphi \sin \theta&= -\theta ^{*}\cos \varphi \cos \theta +\varphi ^{*}\sin \varphi \sin \theta , \\ -Q_{1}\cos \theta -Q_{3}\cos \varphi \sin \theta&= \theta ^{*}\sin \varphi \cos \theta +\varphi ^{*}\cos \varphi \sin \theta , \\ Q_{1}\sin \varphi \sin \theta +Q_{2}\cos \varphi \sin \theta&= -\theta ^{*}\cos \theta \end{aligned}$$

where $Q_{i}$’s are the coordinates of $q(t)$ for $i=1,2,3$. The matrix of coefficients of unknows $Q_{1},Q_{2},$ and $Q_{3}$ is skew a symmetric matrix

$$\begin{aligned} \left[ \begin{array}{ccc} 0 &{}\quad \cos \theta &{}\quad -\sin \varphi \sin \theta \\ -\cos \theta &{}\quad 0 &{}\quad -\cos \varphi \sin \theta \\ \sin \varphi \sin \theta &{}\quad \cos \varphi \sin \theta &{}\quad 0 \end{array} \right] \end{aligned}$$

and therefore its rank is $2$ with $\theta (t)\ne 2k\pi ,k\in \mathbb {Z}$. The rank of the augmented matrix

$$\begin{aligned} \left[ \begin{array}{c@{\quad }c@{\quad }c} 0 &{} \cos \theta &{} -\sin \varphi \sin \theta \\ -\cos \theta &{} 0 &{} -\cos \varphi \sin \theta \\ \sin \varphi \sin \theta &{} \cos \varphi \sin \theta &{} 0 \end{array} \begin{array}{c} -\theta ^{*}\cos \varphi \cos \theta +\varphi ^{*}\sin \varphi \sin \theta \\ \theta ^{*}\sin \varphi \cos \theta +\varphi ^{*}\cos \varphi \sin \theta \\ -\theta ^{*}\cos \theta \end{array} \right] \end{aligned}$$

is $2$. Thus this system of linear equations have infinite solutions given by

$$\begin{aligned} Q_{1}&= -\left( Q_{3}+\varphi ^{*}\right) \cos \varphi \tan \theta -\theta ^{*}\sin \varphi , \nonumber \\ Q_{2}&= \left( Q_{3}+\varphi ^{*}\right) \sin \varphi \tan \theta -\theta ^{*}\cos \varphi , \\ Q_{3}&= Q_{3}. \nonumber \end{aligned}$$

(4.2)

Since $Q_{3}(t)$ can be chosen arbitrarily, we may take that $Q_{3}(t)=-\varphi ^{*}(t)$. In this case, (4.2) reduces to

$$\begin{aligned} Q_{1}&= -\theta ^{*}\sin \varphi , \nonumber \\ Q_{2}&= -\theta ^{*}\cos \varphi , \\ Q_{3}&= -\varphi ^{*}. \nonumber \end{aligned}$$

(4.3)

The distribution parameter of the ruled surface given (3.2 ) is obtained as follows

$$\begin{aligned} \Delta =\frac{\left\langle \frac{d\sigma }{dt},\frac{d\sigma ^{*}}{dt} \right\rangle }{\left\| \frac{d\sigma }{dt}\right\| ^{2}}=\frac{ \frac{d\varphi ^{*}}{dt}\frac{d\varphi }{dt}\sin ^{2}\theta +\theta ^{*}\left( \frac{d\varphi }{dt}\right) ^{2}\sin \theta \cos \theta + \frac{d\theta ^{*}}{dt}\frac{d\theta }{dt}}{\left( \frac{d\varphi }{dt} \right) ^{2}\sin ^{2}\theta +\left( \frac{d\theta }{dt}\right) ^{2}}. \end{aligned}$$

(4.4)

If this spherical orthotomic ruled surface is developable, then $\Delta =0$ and by (4.4), we get

$$\begin{aligned} \frac{d\varphi ^{*}}{dt}\frac{d\varphi }{dt}\sin ^{2}\theta +\theta ^{*}\left( \frac{d\varphi }{dt}\right) ^{2}\sin \theta \cos \theta + \frac{d\theta ^{*}}{dt}\frac{d\theta }{dt}=0. \end{aligned}$$

Setting

$$\begin{aligned} y(t)=\cot \theta ,\quad A(t)=-\frac{\theta ^{*}\left( \frac{d\varphi }{dt} \right) ^{2}}{\frac{d\theta ^{*}}{dt}},\quad B(t)=-\frac{\frac{d\varphi ^{*}}{dt}\frac{d\varphi }{dt}}{\frac{d\theta ^{*}}{dt}} \end{aligned}$$

we are lead to a linear differential equation of first order

$$\begin{aligned} \frac{dy}{dt}+A(t)y+B(t)=0. \end{aligned}$$

(4.5)

If we assume that $\varphi (t)$ and $\theta (t)$ are both constants, then (4.5) is identically zero, that is, the spherical orthotomic ruled surface $\widehat{\sigma }(t)$ is a cylinder.

Let $q(t)$ be a curve. Then we can find a developable spherical orthotomic ruled surface such that, its base curve is the curve $q(t)$ and by (4.3), we have

$$\begin{aligned} \tan \varphi =\frac{Q_{1}}{Q_{2}},\quad \text { }\theta ^{*}=\pm \sqrt{ Q_{1}^{2}+Q_{2}^{2}}\quad \text { and }\quad \varphi ^{*}=-Q_{3}. \end{aligned}$$

(4.6)

Now we need to determine $\theta (t)$. The solution of (4.5) gives $\cot \theta$. This solution includes an integral constant, thus we have infinitely many developable spherical orthotomic ruled surfaces such that each of them has a base curve $q(t)$.

Moreover, note that $\theta ^{*}(t)$, given by (4.6), has two values; by using the minus sign, then we obtain the reciprocal of the spherical orthotomic ruled surfaces obtained by using the plus sign for a given integral constant.

Example 1

Consider the curve $q(t)=(t^{2},t^{2},2t+1)$

Then

$$\begin{aligned} \tan \varphi =1,\text { }\theta ^{*}=t\sqrt{2},\quad \text {and }\quad \varphi ^{*}=-2t-1 \end{aligned}$$

and

$$\begin{aligned} \frac{d\varphi ^{*}}{dt}=2,\text { }\frac{d\varphi }{dt}=0\quad \text { and }\quad \frac{d\theta ^{*}}{dt}=\sqrt{2} \end{aligned}$$

we substitute these values into (4.5) and solve this differential equation

$$\begin{aligned} y=\cot \theta =C,\quad C\in \mathbb {R}. \end{aligned}$$

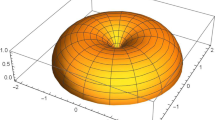
Hence, the family of the developable ruled surface is given by

$$\begin{aligned} m(u,t)=q(t)+u\sigma (t), \end{aligned}$$

where

$$\begin{aligned} \sigma (t)=\left( -\frac{Q_{1}}{\theta ^{*}}\sin \theta ,-\frac{Q_{2}}{\theta ^{*}}\sin \theta ,\cos \theta \right) . \end{aligned}$$

The graph of the developable spherical orthotomic ruled surface given by this equation for $C=0$ in domain

$$\begin{aligned} D:\left\{ \begin{array}{c} -2\le t\le 2 \\ -4\le u\le 4 \end{array} \right. \end{aligned}$$

is given in Figure 1.

Fig. 1

Spherical orthotomic ruled surface

For the spherical orthotomic of the great circle which lies on the $\overrightarrow{\widehat{e}}_{1} \overrightarrow{\widehat{e}}_{3}$ plane, relative to the dual curve $\widehat{x}$ is

$$\begin{aligned} \widehat{\sigma }(t)&= \left( \cos \varphi (t)\sin \theta (t),-\sin \varphi (t)\sin \theta (t),\cos \theta (t)\right) \\&+\varepsilon \left( \begin{array}{c} \theta ^{*}(t)\cos \varphi (t)\cos \theta (t)-\varphi ^{*}(t)\sin \varphi (t)\sin \theta (t), \\ -\theta ^{*}(t)\sin \varphi (t)\cos \theta (t)-\varphi ^{*}(t)\cos \varphi (t)\sin \theta (t),-\theta ^{*}(t)\sin \theta (t) \end{array} \right) . \end{aligned}$$

We obtain the distribution parameter same as the first choosing. But in this case unknowns $Q_{1},Q_{2},$ and $Q_{3}$ are

$$\begin{aligned} Q_{1}&= \theta ^{*}\sin \varphi , \nonumber \\ Q_{2}&= \theta ^{*}\cos \varphi , \\ Q_{3}&= -\varphi ^{*}. \nonumber \end{aligned}$$

(4.7)

Consider the same curve $q(t)=(t^{2},t^{2},2t+1),$ the spherical orthotomic ruled surface is obtained as

$$\begin{aligned} m(u,t)=\left( t^{2}+\frac{ut}{\sqrt{2}},t^{2}-\frac{ut}{\sqrt{2}},2t+1\right) . \end{aligned}$$

The graph is the same as the previous.

For the plane spanned by $\left\{ \overrightarrow{\widehat{e}}_{1}, \overrightarrow{\widehat{e}}_{2}\right\} ,$ we obtain the same distribution parameter and the same differential equation with

$$\begin{aligned} Q_{1}&= \theta ^{*}\sin \varphi , \\ Q_{2}&= -\theta ^{*}\cos \varphi , \\ Q_{3}&= -\varphi ^{*}. \end{aligned}$$

For $q(t)=(t^{2},t^{2},2t+1),$ the spherical orthotomic ruled surface is

$$\begin{aligned} m(u,t)=\left( t^{2}-\frac{ut}{\sqrt{2}},t^{2}+\frac{ut}{\sqrt{2}},2t+1\right) . \end{aligned}$$

and the graph is the same as the other ones.