A new PDE approach to the large time asymptotics of solutions of Hamilton–Jacobi equations

Abstract

We introduce a new PDE approach to establishing the large time asymptotic behavior of solutions of Hamilton–Jacobi equations, which modifies and simplifies the previous ones (Barles et al. in Arch Ration Mech Anal 204(2):515–558, 2012; Barles and Souganidis in SIAM J Math Anal 31(4):925–939, 2000), under a refined “strict convexity” assumption on the Hamiltonians. Not only such “strict convexity” conditions generalize the corresponding requirements on the Hamiltonians in Barles and Souganidis (SIAM J Math Anal 31(4):925–939, 2000), but also one of the most refined our conditions covers the situation studied in Namah and Roquejoffre (Commun Partial Differ Equ 24(5–6):883–893, 1999).

1 Introduction

In this article we introduce a new PDE approach to establishing the large time asymptotic behavior of solutions of Hamilton–Jacobi equations.

In the last two decades there have been major developments in the study of the large time asymptotics of solutions of Hamilton–Jacobi equations, initiated by the work by Namah and Roquejoffre [19] and by Fathi [9].

The approach by Fathi is based on the weak KAM theory and the representation of solutions of the Hopf-Lax-Oleinik type or, in other words, as the value functions of optimal control, and has a wide scope which is different from the one in Namah–Roquejoffre [19]. The optimal control/dynamical approach of Fathi has been subsequently developed for further applications and technical improvements by many authors (see, for instance, [8, 10, 12, 14, 15, 17, 18]).

At the beginning of the developments mentioned above, another approach has been introduced by the first author and Souganidis [5], which does not depend on the representation formulas of solutions and thus applies to a more general class of Hamilton–Jacobi equations including those with non-convex Hamiltonians. We refer for recent developments in this direction to [3, 4].

We also refer [3] for further comments and references related to the large time asymptotics of solutions of Hamilton–Jacobi equations and [6] for a new development on this study for the general degenerate viscous Hamilton-Jacobi equations.

Our aim here is to modify and slightly simplify the main ingredient in the PDE approach by the first author and Souganidis [5] as well as to refine the requirements on the Hamiltonians.

To clarify and simplify the presentation, we consider the asymptotic problem in the periodic setting. We are thus concerned with the Cauchy problem

$$\begin{aligned} \left\{ \begin{array}{ll} u_t(x,t)+H(x,D_x u(x,t))=0 &{} \text{ in }\; Q,\\ u(x,0)=u_0(x) &{} \text{ for }\; x\in \mathbb{R }^n, \end{array} \right. \end{aligned}$$

(CP)

where $Q:=\mathbb{R }^n\times (0,\infty )$, $u$ represents the unknown function on $\,\overline{\!Q}, u_t=u_t(x,t)=(\partial u/\partial t)(x,t), D_xu(x,t)=((\partial u/\partial x_1)(x,t),...,(\partial u/\partial x_n)(x,t))$ and $u_0$ represents the initial data. The functions $u(x,t)$ and $u_0(x)$ are supposed to be periodic in $x$.

We make the following assumptions throughout this article:

• (A1) The function $u_0$ is continuous in $\mathbb{R }^n$ and periodic with period $\mathbb{Z }^n$.

• (A2) $H\in C(\mathbb{R }^n\times \mathbb{R }^n)$.

• (A3) The Hamiltonian $H(x,p)$ is periodic in $x$ with period $\mathbb{Z }^n$ for every $p\in \mathbb{R }^n$.

• (A4) The Hamiltonian $H$ is coercive. That is,

  $$\begin{aligned} \lim _{r\rightarrow \infty }\inf \{H(x,p): (x,p)\in \mathbb{R }^{2n},\, |p|\ge r\}=\infty . \end{aligned}$$

Our notational conventions are as follows. We may regard functions $f(x)$ on $\mathbb{R }^n$ (resp., $g(x,y)$ on $\mathbb{R }^n\times V$, where $V$ is a subset of $\mathbb{R }^m$) periodic in $x\in \mathbb{R }^n$ with period $\mathbb{Z }^n$ as functions on the torus $\mathbb{T }^n$ (resp., $\mathbb{T }^n\times V$). In this viewpoint, we write $C(\mathbb{T }^n)$, $C(\mathbb{T }^n\times V)$, etc, for the subspaces of all functions $f(x)$ in $C(\mathbb{R }^n)$, of all functions $g(x,y)$ in $C(\mathbb{R }^n\times V)$, etc, periodic in $x$ with period $\mathbb{Z }^n$. We denote the sup-norm (or the $L^\infty$-norm) of a function $f$ by $\Vert f\Vert _\infty$ and $\Vert f\Vert _{L^\infty }$ interchangeably. Regarding the notion of solution of Hamilton–Jacobi equations, in this article we will be only concerned with viscosity solutions, viscosity subsolutions and viscosity supersolutions, which we refer simply as solutions, subsolutions and supersolutions. For any $R>0$, $B_R$ denotes the open ball of $\mathbb{R }^n$ with center at the origin and radius $R$. For any $X\subset \mathbb{R }^n$, $\,\mathrm{UC}\,(X)$ and $\mathrm{Lip}(X)$ denote the spaces of all uniformly continuous functions and all Lipschitz continuous functions on $X$, respectively.

We now recall the following basic results.

Theorem 1

Under the hypotheses (A1)–(A4), there exists a unique solution $u\in \,\mathrm{UC}\,(\mathbb{T }^n\times [0,\,\infty ))$ of (CP). Furthermore, if $u_0\in \mathrm{Lip}(\mathbb{T }^n)$, then $u\in \mathrm{Lip}(\mathbb{T }^n\times [0,\,\infty ))$.

Theorem 2

Under the hypotheses (A2)–(A4), let $u,\,v\in \,\mathrm{UC}\,(\mathbb{T }^n\times [0,\,\infty ))$ be solutions of

$$\begin{aligned} u_t+H(x,D_xu)=0 \quad \text{ in } \; Q. \end{aligned}$$

(HJ)

Then

$$\begin{aligned} \Vert u-v\Vert _{L^\infty (Q)}\le \Vert u(\cdot , 0)-v(\cdot ,\,0)\Vert _{L^\infty (\mathbb{R }^n)}. \end{aligned}$$

Theorem 3

Under the hypotheses (A2)–(A4), there exists a unique constant $c\in \mathbb{R }$ such that the problem

$$\begin{aligned} H(x,Dv(x))=c \quad \text{ in } \; \mathbb{R }^n \end{aligned}$$

(EP)

has a solution $v\in \mathrm{Lip}(\mathbb{T }^n)$.

These theorems are classical results in viscosity solutions theory. For instance, the existence part of Theorem 1 is a consequence of Corollaire II.1 in [1]. Under assumptions (A2) and (A3), as is well known, the comparison principle holds between bounded semicontinuous sub and supersolutions of (CP) if one of them is Lipschitz continuous. This comparison result and the existence part of Theorem 1 assure that for each continuous solution $u$ of (CP) there is a sequence $\{u_k\}_{k\in \mathbb{N }}$ of Lipschitz continuous solutions of (CP), with $u_0$ replaced by $u_k(\cdot ,0)$, which converges to $u$ uniformly in $\,\overline{\!Q}$. The existence of such a sequence of Lipschitz continuous solutions of (CP) and the comparison principle for Lipschitz continuous solutions of (CP) guarantees the Theorem 2 holds. Theorem 3 and its proof can be found in [16].

The problem of finding a pair $(c,v)\in \mathbb{R }\times C(\mathbb{T }^n)$, where $v$ satisfies (EP) in the viscosity sense, is called an additive eigenvalue problem or ergodic problem. Thus, for such a pair $(c,v)$, the function $v$ (resp., the constant $c$) is called an additive eigenfunction (resp., eigenvalue).

We note that the conditions (A2)–(A4) are invariant under addition of constants. Hence, by replacing $H$ by $H-c$, with $c$ being the additive eigenvalue of (EP), we may normalize so that the additive eigenvalue $c$ is zero. Thus, in what follows, we always assume that

• (A5) $c=0$, where $c$ denotes the additive eigenvalue.

Accordingly, problem (EP) becomes simply a stationary problem

$$\begin{aligned} H(x,\,Dv(x))=0 \quad \text{ in } \; \mathbb{R }^n. \end{aligned}$$

(1)

The crucial assumptions in this article are the following conditions.

(A6)$_{\scriptscriptstyle +}$ There exist constants $\eta _0>0$ and $\theta _0>1$ and for each $(\eta ,\theta )\in (0,\eta _0)\times (1,\theta _0)$ a constant $\psi =\psi (\eta ,\theta )>0$ such that for all $x, p,q\in \mathbb{R }^n$, if $H(x,p)\le 0$ and $H(x,q)\ge \eta$, then

$$\begin{aligned} H(x,p+\theta (q-p))\ge \eta \theta +\psi . \end{aligned}$$

(A6)$_{\scriptscriptstyle -}$ There exist constants $\eta _0>0$ and $\theta _0>1$ and for each $(\eta ,\theta )\in (0,\eta _0)\times (1,\theta _0)$ a constant $\psi =\psi (\eta ,\theta )>0$ such that for all $x, p,q\in \mathbb{R }^n$, if $H(x,p)\le 0$ and $H(x,q)\ge -\eta$, then

$$\begin{aligned} H(x,p+\theta (q-p))\ge -\eta \theta +\psi . \end{aligned}$$

We will furthermore modify and refine these conditions [see (A9)$_{\scriptscriptstyle \pm }$] in Sect. 4, one of which covers the situation studied by Namah–Roquejoffre [19]. An important consequence is that our PDE method gives a unified approach to most of the large time asymptotic convergence results for (CP) in the literature.

The assumptions above are some kind of strict convexity requirements and they are satisfied if $H$ is strictly convex in $p$. Indeed in this case, since $q = \theta ^{-1}(p+\theta (q-p)) +(1-\theta ^{-1})p$,

$$\begin{aligned} H(x,q)&< \theta ^{-1}H(x, p+\theta (q-p)) + (1-\theta ^{-1})H(x, p)\\&< \theta ^{-1}H(x, p+\theta (q-p)) , \end{aligned}$$

and $\psi$ measures how strict is this inequality. We point out that, for (A6)$_{\scriptscriptstyle -}$, this argument is valid if $p\ne q$ and the inequality is obvious if $p=q$, while in the case of (A6)$_{\scriptscriptstyle +}$ clearly we have always $p\ne q$.

One may have another interpretation of these assumptions, namely that the function $H(x,r)$, as a function of $r$, grows more than linearly on the line segment connecting from $q$ to $p+\theta _0(q-p)$ for some $\theta _0>1$ (notice that this growth rate is negative in the case of (A6)$_{\scriptscriptstyle -}$).

We conclude these remarks on (A6)$_{\scriptscriptstyle \pm }$ by pointing out that (A6)$_{\scriptscriptstyle +}$ is an assumption on the behavior of $H$ on the set $\{H\ge 0\}$ while (A6)$_{\scriptscriptstyle -}$ is an assumption on the behavior of $H$ on the set $\{H\le 0\}$. We refer to Sect. 3 for more precise comments in this direction.

A condition similar to (A6)$_{\scriptscriptstyle +}$ has appeared first in Barles–Souganidis [5] (see (H4) in [5]). Our condition (A6)$_{\scriptscriptstyle +}$ is less stringent and has a wider application than (A6)$_{\scriptscriptstyle +}$ in [3]. For this comparison, see Sect. 3. Also, (A6)$_{\scriptscriptstyle -}$ is less stringent than (A6)$_{\scriptscriptstyle -}$ in [3]. A type of condition (A6)$_{\scriptscriptstyle -}$ has first introduced in Ichihara–Ishii [11] for convex Hamiltonians (see the condition (16) in [11]).

We establish the following theorem by a PDE approach which modifies and simplifies the previous ones in [3, 5].

Theorem 4

Assume that (A1)–(A5) hold and that either (A6)$_{\scriptscriptstyle +}$ or (A6)$_{\scriptscriptstyle -}$ holds. Then the unique solution $u(x,t)$ in $\,\mathrm{UC}\,(\mathbb{T }^n\times [0,\,\infty ))$ of (CP) converges uniformly in $\mathbb{R }^n$, as $t\rightarrow \infty$, to a function $u_\infty (x)$ in $\mathrm{Lip}(\mathbb{T }^n)$, which is a solution of (1).

A generalization of the theorem above is given in Sect. 4 (see Theorem 11), which covers the main result in [19] in the periodic setting.

In Sect. 2, we give an explanation of the new ingredient in our new PDE method, a (hopefully transparent) formal proof of Theorem 4 by the new PDE method and its exact version. In Sect. 3, we make comparisons between (A6)$_{\scriptscriptstyle \pm }$ and its classical versions, and discuss convexity-like properties of the Hamiltonians $H$ implied by (A6)$_{\scriptscriptstyle \pm }$ as well as a couple of conditions equivalent to (A6)$_{\scriptscriptstyle \pm }$. In Sect. 4, we present a theorem, with (A6)$_{\scriptscriptstyle \pm }$ replaced by refined conditions, which includes the situation in [19] as a special case.

2 Proof of Theorem 4

Throughout this section, we assume that (A1)–(A5) hold. The first step consists in reducing to the case when $u_0\in \mathrm{Lip}(\mathbb{T }^n)$ and therefore $u$ is Lipschitz continuous on $\mathbb{T }^n\times [0,\,\infty )$.

Lemma 5

If the result of Theorem 4 holds for any $u_0 \in \mathrm{Lip}(\mathbb{T }^n)$ then it holds for any $u_0 \in C(\mathbb{T }^n)$.

Proof

For a general $u_0\in C(\mathbb{T }^n)$ we select a sequence $\{u_{0,j}\}_{j\in \mathbb{N }}\subset \mathrm{Lip}(\mathbb{T }^n)$ which converges to $u_0$ uniformly in $\mathbb{R }^n$. For each $j\in \mathbb{N }$ let $u_j\in \mathrm{Lip}(\mathbb{T }^n\times [0,\,\infty ))$ be the unique solution of (CP), with $u_{0,j}$ in place of $u_0$. By Theorem 2, we have

$$\begin{aligned} \Vert u_j-u_k\Vert _{L^\infty (Q)}\le \Vert u_{0,j}-u_{0,k}\Vert _{L^\infty (\mathbb{R }^n)} \quad \text{ for } \text{ all } \, j,k\in \mathbb{N }. \end{aligned}$$

(2)

Since Theorem 4 holds for any initial data in $\mathrm{Lip}(\mathbb{T }^n)$, we know that for each $j\in \mathbb{N }$ there exists a function $u_{\infty ,j}\in C(\mathbb{T }^n)$ such that $\lim _{t\rightarrow \infty }u_j(x,t)=u_{\infty ,j}(x)$ uniformly in $\mathbb{R }^n$. This implies

$$\begin{aligned} \Vert u_{\infty ,j}-u_{\infty ,k}\Vert _{L^\infty (\mathbb{R }^n)}\le \Vert u_j-u_k\Vert _{L^\infty (Q)} \quad \text{ for } \text{ all } \, j,k\in \mathbb{N }, \end{aligned}$$

which together with (2) yields

$$\begin{aligned} \Vert u_{\infty ,j}-u_{\infty ,k}\Vert _{\infty }\le \Vert u_{0,j}-u_{0,k}\Vert _\infty \quad \text{ for } \text{ all } \, j,k\in \mathbb{N }. \end{aligned}$$

Hence there is a function $u_\infty \in C(\mathbb{T }^n)$ such that $\lim _{j\rightarrow \infty }u_{\infty ,j}(x)=u_\infty (x)$ uniformly in $\mathbb{R }^n$.

Observe by using Theorem 2 that for any $j\in \mathbb{N }$,

$$\begin{aligned} \Vert u(\cdot ,t)-u_\infty \Vert _\infty&\le \Vert u(\cdot ,t)-u_j(\cdot ,t)\Vert _\infty +\Vert u_j(\cdot ,t)-u_{\infty ,j}\Vert _\infty +\Vert u_{\infty ,j}-u_\infty \Vert _\infty \\&\le \Vert u_0-u_{0,j}\Vert _\infty +\Vert u_j(\cdot ,t)-u_{\infty ,j}\Vert _\infty +\Vert u_{\infty ,j}-u_\infty \Vert _\infty , \end{aligned}$$

from which we conclude that $\lim _{t\rightarrow \infty }\Vert u(\cdot ,t)-u_\infty \Vert _{\infty }=0$. By the stability property of viscosity solutions, we see that $u_\infty$ is a solution of (1) and, consequently, $u_\infty \in \mathrm{Lip}(\mathbb{R }^n)$ by Theorem 3. $\square$

Now we turn to the proof of Theorem 4 when $u_0 \in \mathrm{Lip}(\mathbb{T }^n)$. By Theorem 1, there exists a unique solution $u\in \mathrm{Lip}(\mathbb{T }^n\times [0,\,\infty ))$ of (CP) and we have to prove that $u(x,t)$ converges uniformly in $\mathbb{R }^n$ to a function $u_\infty (x)$ as $t\rightarrow \infty$.

Henceforth in this section we assume that $u_0\in \mathrm{Lip}(\mathbb{T }^n)$ and hence the solution $u$ of (CP) is in $\mathrm{Lip}(\mathbb{T }^n\times [0,\,\infty ))$. Also, we fix a solution $v_0\in \mathrm{Lip}(\mathbb{T }^n)$ of (1). Such a function $v_0$ exists thanks to Theorem 3. We set $L:=\max \{\Vert D_x u\Vert _\infty , \Vert D_x v_0\Vert _\infty \}$.

If we set $z(x,t)=v_0(x)$ and invoke Theorem 2, then we get

$$\begin{aligned} \Vert u-z\Vert _{L^\infty (Q)}\le \Vert u_0-v_0\Vert _{L^\infty (\mathbb{R }^n)}, \end{aligned}$$

which shows that $u$ is bounded in $\,\overline{\!Q}$. We may assume by adding a constant to $v_0$ if needed that for some constant $C_0>0$,

$$\begin{aligned} 0\le u(x,t)-v_0(x)\le C_0 \quad \text{ for } \text{ all } \, (x,t)\in \,\overline{\!Q}. \end{aligned}$$

2.1 Under assumption (A6)$_{\scriptscriptstyle +}$

Throughout this subsection we assume, in addition to (A1)–(A5), that (A6)$_{\scriptscriptstyle +}$ holds. Let $\eta _0>0$ and $\theta _0>1$ be the constants from (A6)$_{\scriptscriptstyle +}$.

For $(\eta ,\theta ) \in (0,\eta _0)\times (1,\theta _0)$, we define the function $w$ on $\,\overline{\!Q}$ by

$$\begin{aligned} w(x,t)=\sup _{s\ge t}[u(x,t)-v_0(x)-\theta (u(x,s)-v_0(x)+\eta (s-t))]. \end{aligned}$$

(3)

The following proposition is crucial in our proof of Theorem 4 under (A6)$_{\scriptscriptstyle +}$. To state the proposition, we introduce the functions $\omega _{H,R}$, with $R>0$, as

$$\begin{aligned} \omega _{H,R}(r)= \sup \{|H(x,p)-H(x,q)| : x\in \mathbb{R }^n,\, p,q\in \,\overline{\!B}_R,\, |p-q|\le r\}. \end{aligned}$$

Note that for each $R>0$, the function $\omega _{H,R}$ is nonnegative and nondecreasing in $[0,\,\infty )$ and $\omega _{H,R}(0)=0$.

Proposition 6

Let $\psi =\psi (\eta ,\theta )>0$ be the constant from (A6)$_{\scriptscriptstyle +}$. Then the function $w$ is a subsolution of

$$\begin{aligned} \min \{w(x,t),w_t(x,t)-\omega _{H,R}(|D_x w(x,t)|)+\psi \}\le 0 \quad \text{ in } \, Q, \end{aligned}$$

(4)

where $R:=(2\theta _0+1)L$.

Our proof of Theorem 4 follows the outline of previous works like [3, 5] where a key result is an asymptotic monotonicity property for $u$. This asymptotic monotonicity is a consequence of Proposition 6 which, roughly speaking, implies that $\min \{u_t,0\} \rightarrow 0$ as $t \rightarrow \infty$. This is rigorously stated in Lemma 8 and its consequence in (27). With assumption (A6)$_{\scriptscriptstyle -}$, this is also the case but with a different monotonicity (i.e., $\max \{u_t,0\} \rightarrow 0$ as $t \rightarrow \infty$).

For this reason, the function $w$ defined by (3) is a kind of Lyapunov function in our asymptotic analysis in a broad sense. The main new aspect in this article, compared to [3, 5], is indeed the simpler form of our $w$, which is defined by taking supremum in $s$ of the function

$$\begin{aligned} u(x,t)-v_0(x)-\theta (u(x,s)-v_0(x)+\eta (s-t)), \end{aligned}$$

whose functional dependence on $u$ and $v_0$ is linear. In the previous works, the function

$$\begin{aligned} \sup _{s\ge t}\frac{u(x,s)-v_0(x)+\eta (s-t)}{u(x,t)-v_0(x)} \end{aligned}$$

(5)

(one should assume here by adding a constant to $v_0$ if necessary that $\inf _{(x,t)\in Q}(u(x,t)-v_0(x))>0$), played the same role as our function $w$, and the value

$$\begin{aligned} \frac{u(x,s)-v_0(x)+\eta (s-t)}{u(x,t)-v_0(x)} \end{aligned}$$

depends nonlinearly in $u$ and $v_0$. One might see that the passage from the function given by (5) to $w$ given by (3) bears a resemblance that from the Kruzkov transform to a linear change in [13] in the analysis of the comparison principle for stationary Hamilton–Jacobi equations.

From a technical point of view, they are a lot of variants for such results. For example, as it is the case in [5], one may look for a variational inequality for $m(t):= \max _{x\in \mathbb{R }^n}w(x,t)$ or for $m(t):= \max _{x\in \overline{\Omega }}w(x,t)$ where $\Omega$ is a suitable domain of $\mathbb{R }^n$. This last form can be typically useful when one wants to couple different assumptions on $H$ on $\Omega$ and its complementary as in [5] where the coupling with Namah–Roquejoffre type assumptions was solved in that way, the point being to control the behavior of $u$ on $\partial \Omega$.

For the connections between our assumptions and Namah–Roquejoffre type assumptions, we refer to Sect. 4.

2.1.1 A formal computation

Here we explain the algebra which bridges condition (A6)$_{\scriptscriptstyle +}$ to Proposition 6 under the strong regularity assumptions that $u,\,w\in C^1(\mathbb{T }^n\times [0,\,\infty ))$ and $v_0\in C^1(\mathbb{T }^n)$ and that for each $(x,t)\in Q$ there exists an $s>t$ such that

$$\begin{aligned} w(x,t)=u(x,t)-v_0(x)-\theta (u(x,s)-v_0(x)+\eta (s-t)). \end{aligned}$$

(6)

Of course, these conditions do not hold in general.

Fix any $(x,t)\in Q$ and an $s>t$ so that (6) holds. If $w(x,t)\le 0$, then (4) holds at $(x,t)$. We thus suppose that $w(x,t)>0$.

Setting

$$\begin{aligned} p=Dv_0(x),\quad q=D_xu(x,s), \quad r=D_xu(x,t),\quad a=u_s(x,s) \quad \text{ and } \quad b=u_t(x,t), \end{aligned}$$

we have

$$\begin{aligned} H(x,p)&\le 0.\end{aligned}$$

(7)

$$\begin{aligned} a+H(x,q)&\ge 0,\end{aligned}$$

(8)

$$\begin{aligned} b+H(x,r)&\le 0, \end{aligned}$$

(9)

Also, by the choice of $s$, we get

$$\begin{aligned} D_xw(x,t)&= r-p-\theta (q-p), \end{aligned}$$

(10)

$$\begin{aligned} w_t(x,t)&= b+\theta \eta , \end{aligned}$$

(11)

$$\begin{aligned} 0&= -\theta (a+\eta ). \end{aligned}$$

(12)

Combining (8) and (12) yields

$$\begin{aligned} H(x,q)\ge \eta . \end{aligned}$$

(13)

Now, in view of inequalities (7) and (13), we may use assumption (A6)$_{\scriptscriptstyle +}$, to get

$$\begin{aligned} H(x,p+\theta (q-p))\ge \theta \eta +\psi . \end{aligned}$$

Using (10), we get

$$\begin{aligned} H(x,r)=H(x,D_xw(x,t)+p+\theta (q-p)). \end{aligned}$$

Using the definition of $L>0$, we clearly have

$$\begin{aligned} |r|=|D_x u(x,t)|\le L \le R,\quad |p+\theta (q-p)|\le (1+2\theta ) L \le R \end{aligned}$$

and therefore we get

$$\begin{aligned} H(x,r)&\ge H(x,p+\theta (q-p))-\omega _{H,R}(|D_xw(x,t)|)\\&\ge -\omega _{H,R}(|D_xw(x,t)|)+\theta \eta +\psi . \end{aligned}$$

This together with (9) and (11) yields

$$\begin{aligned} 0&\ge b+H(x,r)=w_t(x,t)-\theta \eta +H(x,r) \\&\ge w_t(x,t)-\theta \eta -\omega _{H,R}(|D_xw(x,t)|) +\theta \eta +\psi \\&= w_t(x,t)-\omega _{H,R}(|D_xw(x,t)|)+\psi . \end{aligned}$$

This shows under our convenient regularity assumptions that (4) holds.

Remark 1

The actual requirement to $v_0$ is just the subsolution property in the above computation, which is true also in the following proof of Theorem 4. Some of subsolutions of (1) may have a better property, which solutions of (1) do not have. This is the technical insight in the generalization of Theorem 4 in Sect. 4.

2.1.2 Proof of Proposition 6

We begin with the following lemma.

Lemma 7

We have

$$\begin{aligned} -C_0(\theta -1)\le w(x,t)\le C_0 \quad \text{ for } \text{ all } \, (x,t)\in \mathbb{R }^n\times [0,\,\infty ). \end{aligned}$$

Proof

We just need to note that for all $(x,t)\in \mathbb{R }^n\times [0,\,\infty )$,

$$\begin{aligned} w(x,t)\ge u(x,t)-v_0(x)-\theta (u(x,t)-v_0(x))&= (1-\theta )(u(x,t)-v_0(x))\\&\ge -C_0(\theta -1), \end{aligned}$$

and

$$\begin{aligned} w(x,t)\le \max _{s\ge t}(u(x,t)-v(x))\le C_0. \end{aligned}$$

$\square$

Proof of Proposition 6

Noting that $u\in \mathrm{Lip}(\mathbb{T }^n\times [0,\,\infty ))$ and $v_0\in \mathrm{Lip}(\mathbb{T }^n)$ and rewriting $w$ as

$$\begin{aligned} w(x,t)=\max _{r\ge 0}(u(x,t)-v_0(x)-\theta (u(x,r+t)-v_0(x)+\eta r)), \end{aligned}$$

we deduce that $w\in \mathrm{Lip}(\mathbb{T }^n\times [0,\,\infty ))$.

Fix any $\phi _0\in C^1(Q)$ and $(\hat{x},\hat{t})\in Q$, and assume that

$$\begin{aligned} \max _{Q}(w-\phi _0)=(w-\phi _0)(\hat{x},\hat{t}). \end{aligned}$$

We intend to prove that for $R=(2\theta _0+1)L$,

$$\begin{aligned} \min \{w, \phi _{0,t}-\omega _{H,R}(|D\phi _0|)+\psi \}\le 0 \quad \text{ at } \, (\hat{x},\hat{t}). \end{aligned}$$

(14)

If $w(\hat{x},\hat{t})\le 0$, then (14) clearly holds. We may thus suppose that $w(\hat{x},\hat{t})>0$. We choose an $\hat{s}\ge \hat{t}$ so that

$$\begin{aligned} w(\hat{x},\hat{t})=u(\hat{x},\hat{t})-v_0(\hat{x})-\theta (u(\hat{x},\hat{s})-v_0(\hat{x})+\eta (\hat{s}-\hat{t})). \end{aligned}$$

Observe that for any $s=\hat{t}$,

$$\begin{aligned} u(\hat{x},\hat{t})-v_0(\hat{x})-\theta (u(\hat{x},s)-v_0(\hat{x})+\eta (s-\hat{t}) = (1-\theta )(u(\hat{x},\hat{t})-v_0(\hat{x}))\le 0, \end{aligned}$$

which guarantees that $\hat{s}>\hat{t}$.

Define the function $\phi \in C^1(Q\times (0,\,\infty ))$ by

$$\begin{aligned} \phi (x,t,s)=\phi _0(x,t)+|x-\hat{x}|^2+(t-\hat{t})^2+(s-\hat{s})^2. \end{aligned}$$

Note that the function

$$\begin{aligned} u(x,t)-v_0(x)-\theta (u(x,s)-v_0(x)+\eta (s-t))-\phi (x,t,s) \end{aligned}$$

on $Q\times (0,\,\infty )$ attains a strict maximum at $(\hat{x},\hat{t},\hat{s})$, and that $D_x\phi (\hat{x},\hat{t},\hat{s})=D_x\phi _0(\hat{x},\hat{t})$, $\phi _t(\hat{x},\hat{t},\hat{s})=\phi _{0,t}(\hat{x},\hat{t})$ and $\phi _s(\hat{x},\hat{t},\hat{s})=0$.

Now, if $B$ is an open ball of $\mathbb{R }^{3n+2}$ centered at $(\hat{x},\hat{x},\hat{x},\hat{t},\hat{s})$ with its closure $\,\overline{\!B}$ contained in $\mathbb{R }^{3n}\times (0,\,\infty )^2$, we use the technique of “tripling variables” and consider the function $\Phi$ on $\,\overline{\!B}$ given by

$$\begin{aligned} \Phi (x,y,z,t,s)&= u(x,t)-v_0(z)-\theta (u(y,s)-v_0(z)+\eta (s-t))\\&-\phi (x,t,s)-\alpha (|x-y|^2+|x-z|^2), \end{aligned}$$

where $\alpha >0$ is a (large) constant.

Let $(x_\alpha ,y_\alpha ,z_\alpha ,t_\alpha ,s_\alpha )\in \,\overline{\!B}$ be a maximum point of $\Phi$. As usual in viscosity solutions theory, we observe that

$$\begin{aligned} \lim _{\alpha \rightarrow \infty }(x_\alpha ,y_\alpha ,z_\alpha ,t_\alpha ,s_\alpha )=(\hat{x},\hat{x},\hat{x},\hat{t},\hat{s}). \end{aligned}$$

Consequently, if $\alpha$ is sufficiently large, then

$$\begin{aligned} (x_\alpha ,y_\alpha ,z_\alpha ,t_\alpha ,s_\alpha )\in B. \end{aligned}$$

We assume henceforth that $\alpha$ is sufficiently large so that the above inclusion holds.

Next, setting

$$\begin{aligned} p_\alpha =2(\theta -1)^{-1}\alpha (z_\alpha -x_\alpha ) \quad \text{ and } \quad q_\alpha =2\theta ^{-1}\alpha (x_\alpha -y_\alpha ), \end{aligned}$$

and noting that

$$\begin{aligned} \Phi (x,y,z,t,s)&= u(x,t)-\theta u(y,s)+(\theta -1)v_0(z)-\theta \eta (s-t)\\&-\phi (x,t,s)-\alpha (|x-y|^2+|x-z|^2), \end{aligned}$$

we observe that

$$\begin{aligned}&p_\alpha \in D^+v_0(z_\alpha ),\end{aligned}$$

(15)

$$\begin{aligned}&\left( q_\alpha ,\,-\theta ^{-1}\phi _s(x_\alpha ,t_\alpha ,s_\alpha )-\eta \right) \in D^-u(y_\alpha ,s_\alpha ),\end{aligned}$$

(16)

$$\begin{aligned}&\big (D_x\phi (x_\alpha ,t_\alpha ,s_\alpha )+\theta q_\alpha -(\theta -1)p_\alpha ,\, \phi _t(x_\alpha ,t_\alpha ,s_\alpha )-\theta \eta \big ) \in D^+u(x_\alpha ,t_\alpha ),\qquad \quad \end{aligned}$$

(17)

By the definition of $L$, we see as usual in viscosity solutions theory that $\max \{|p_\alpha |,\,|q_\alpha |\}\le L$. Sending $\alpha \rightarrow \infty$ in (15)–(17) along an appropriate sequence, we find points $\hat{p},\,\hat{q}\in \,\overline{\!B}_L$ such that

$$\begin{aligned}&\hat{p}\in \,\overline{\!D}{}^+v_0(\hat{x}),\end{aligned}$$

(18)

$$\begin{aligned}&\left( \hat{q},\,-\theta ^{-1}\phi _s(\hat{x},\hat{t},\hat{s})-\eta \right) \in \,\overline{\!D}{}^-u(\hat{x},\hat{s}),\end{aligned}$$

(19)

$$\begin{aligned}&\left( D_x\phi (\hat{x},\hat{t},\hat{s})+\theta \hat{q}-(\theta -1)\hat{p},\, \phi _t(\hat{x},\hat{t},\hat{s})-\theta \eta \right) \in \,\overline{\!D}{}^+u(\hat{x},\hat{t}), \end{aligned}$$

(20)

where $\,\overline{\!D}{}^\pm$ stand for the closures of $D^\pm$, for instance, $\,\overline{\!D}^+u(\hat{x},\hat{s})$ denotes the set of points $(q,b)\in \mathbb{R }^n\times \mathbb{R }$ for which there are sequences $\{(q_j,b_j)\}_{j}\subset \mathbb{R }^n\times \mathbb{R }$ and $\{(x_j,s_j)\}_{j}\subset Q$ such that $\lim _{j}(q_j,b_j,x_j,s_j)=(q,b,\hat{x},\hat{s})$ and $(q_j,b_j)\in D^+u(x_j,s_j)$ for all $j$. Here recall that $\phi _s(\hat{x},\hat{t},\hat{s})=0$, $\phi _t(\hat{x},\hat{t},\hat{s})=\phi _{0,t}(\hat{x},\hat{t})$ and $D_x\phi (\hat{x},\hat{t},\hat{s})=D_x\phi _0(\hat{x},\hat{t})$.

From (18) and (19), we get $H(\hat{x},\hat{p}\,)\le 0$ and

$$\begin{aligned} -\eta +H(\hat{x},\hat{q}\,)\ge 0. \end{aligned}$$

By condition (A6)$_{\scriptscriptstyle +}$, we get

$$\begin{aligned} H(\hat{x},\hat{p}+\theta (\hat{q}-\hat{p}))\ge \theta \eta +\psi . \end{aligned}$$

(21)

From (20), we get

$$\begin{aligned} 0\ge \phi _{0,t}(\hat{x},\hat{t})-\theta \eta +H(\hat{x},D_x\phi _0(\hat{x},\hat{t})+\theta \hat{q}-(\theta -1)\hat{p}). \end{aligned}$$

(22)

Noting that $|\hat{p}+\theta (\hat{q}-\hat{p})|\le (1+2\theta )L\le R$ and $|D_x\phi _0(\hat{x},\hat{t})+\theta \hat{q}-(\theta -1)\hat{p}|\le L$ because of (20) and combining (22) and (21), we get

$$\begin{aligned} 0&\ge \phi _{0,t}(\hat{x},\hat{t}\,)-\theta \eta +H(\hat{x},\hat{p}+\theta (\hat{q}-\hat{p}))-\omega _{H,R}(|D_x\phi _0(\hat{x},\hat{t}\,)|)\\&\ge \phi _{0,t}(\hat{x},\hat{t}\,)-\omega _{H,R}(|D_x\phi _0(\hat{x},\hat{t}\,)|)+\psi , \end{aligned}$$

which shows that (14) holds. $\square$

2.1.3 Completion of the proof of Theorem 4 under (A6)$_{\scriptscriptstyle +}$

We set

$$\begin{aligned} w_\infty (x)=\limsup _{t\rightarrow \infty }w(x,t) \quad \text{ for } \text{ all } \, x\in \mathbb{R }^n. \end{aligned}$$

Lemma 8

We have

$$\begin{aligned} w_\infty (x)\le 0 \quad \text{ for } \text{ all } \, x\in \mathbb{R }^n. \end{aligned}$$

Moreover, the convergence

$$\begin{aligned} \lim _{t\rightarrow \infty }\max \{w(x,t),\,0\}=0 \end{aligned}$$

(23)

is uniform in $x\in \mathbb{R }^n$.

Proof

It is sufficient to prove that the convergence (23) holds uniformly in $x\in \mathbb{R }^n$. Contrary to this, we suppose that there is a sequence $(x_j,t_j)\in Q$ such that $\lim _{j\rightarrow \infty }t_j=\infty$ and $w(x_j,t_j)\ge \delta$ for all $j\in \mathbb{N }$ and some constant $\delta >0$. In view of the periodicity of $w$, we may assume that $\lim _{j\rightarrow \infty }x_j=y$ for some $y\in \mathbb{R }^n$. Moreover, in view of the Ascoli–Arzela theorem, we may assume by passing to a subsequence of $\{(x_j,t_j)\}$ if needed that

$$\begin{aligned} \lim _{j\rightarrow \infty } w(x,t+t_j)=f(x,t) \quad \text{ locally } \text{ uniformly } \text{ in } \, \mathbb{R }^n\times (-\infty ,+\infty ), \end{aligned}$$

for some bounded function $f\in \mathrm{Lip}(\mathbb{T }^n\times \mathbb{R })$.

Now, note that $f(y,0)\ge \delta$. By the stability of the subsolution property under uniform convergence, we see that $f$ is a subsolution of

$$\begin{aligned} \min \{f(x,t),\,f_t(x,t)-\omega _{H,R}(|D_x f(x,t)|)+\psi \}\le 0 \quad \text{ in } \, \mathbb{R }^{n+1}. \end{aligned}$$

(24)

Since $f\in C(\mathbb{T }^n\times \mathbb{R })$ and $f$ is bounded on $\mathbb{R }^{n+1}$, for every $\varepsilon >0$ the function $f(x,t)-\varepsilon t^2$ attains a maximum over $\mathbb{R }^{n+1}$ at a point $(x_\varepsilon ,t_\varepsilon )$. Observe as usual in the viscosity solutions theory that

$$\begin{aligned} f(x_\varepsilon ,t_\varepsilon )-\varepsilon t_\varepsilon ^2 \ge f(y,0)\ge \delta , \end{aligned}$$

and therefore

$$\begin{aligned} f(x_\varepsilon ,t_\varepsilon )\ge \delta \quad \text{ and } \quad \varepsilon |t_\varepsilon |\le (\varepsilon \Vert f\Vert _\infty )^{1/2}. \end{aligned}$$

In particular, we have $\lim _{\varepsilon \rightarrow 0+}\varepsilon t_\varepsilon =0$. In view of inequality (24), we get

$$\begin{aligned} 2\varepsilon t_\varepsilon -\omega _{H,R}(0)+\psi \le 0, \end{aligned}$$

which, in the limit as $\varepsilon \rightarrow 0+$, yields $\psi \le 0$, a contradiction. This shows that the uniform convergence (23) holds.

Proof of Theorem 4 under (A6)$_{\scriptscriptstyle +}$ Let $w$ be the function defined by (3), with arbitrary $(\eta ,\theta )\in (0,\eta _0)\times (0,\theta _0)$.

Fix any $\varepsilon >0$. Thanks to (23), we may choose a constant $T_\varepsilon \equiv T_{\varepsilon ,\eta ,\theta }>0$ so that for any $t\ge T_\varepsilon$,

$$\begin{aligned} w(x,t)\le \varepsilon \quad \text{ for } \text{ all } \; x\in \mathbb{R }^n. \end{aligned}$$

Let $t\ge T_\varepsilon$ and $x\in \mathbb{R }^n$. From the above, for any $s\ge t$, we have

$$\begin{aligned} u(x,t)-v_0(x)&\le \varepsilon +\theta (u(x,s)-v_0(x))+\theta \eta (s-t)\\&= \varepsilon +u(x,s)-v_0(x)+(\theta -1)(u(x,s)-v_0(x))+\theta \eta (s-t)\\&\le \varepsilon +u(x,s)-v_0(x)+(\theta -1)C_0+\theta \eta (s-t). \end{aligned}$$

Thus, for any $0\le s\le 1$, we have

$$\begin{aligned} u(x,t)\le u(x,t+s)+(\theta -1)C_0+\theta \eta +\varepsilon . \end{aligned}$$

(25)

Now, since $u$ is bounded and Lipschitz continuous in $\,\overline{\!Q}$, in view of the Ascoli–Arzela theorem, we may choose a sequence $\tau _j\rightarrow \infty$ and a bounded function $z\in \mathrm{Lip}(\mathbb{T }^n \times (-\infty ,+\infty ))$ so that

$$\begin{aligned} \lim _{j\rightarrow \infty } u(x,t+\tau _j)=z(x,t) \quad \text{ locally } \text{ uniformly } \text{ on } \; \mathbb{R }^{n+1}. \end{aligned}$$

(26)

By (25) we get

$$\begin{aligned} z(x,t)\le z(x,t+s) +(\theta -1)C_0+\theta \eta +\varepsilon \quad \text{ for } \text{ all } \; (x,t,s)\in \mathbb{R }^{n+1}\times [0,\,1]. \end{aligned}$$

This is valid for all $(\eta ,\theta )\in (0,\eta _0)\times (1,\theta _0)$. Hence,

$$\begin{aligned} z(x,t)\le z(x,t+s)+\varepsilon \quad \text{ for } \text{ all } \; (x,t,s)\in \mathbb{R }^{n+1}\times [0,\,1], \end{aligned}$$

and moreover

$$\begin{aligned} z(x,t)\le z(x,t+s) \quad \text{ for } \text{ all } \; (x,t,s)\in \mathbb{R }^{n+1}\times [0,\,1]. \end{aligned}$$

(27)

Thus we find that the function $z(x,t)$ is nondecreasing in $t\in \mathbb{R }$ for all $x\in \mathbb{R }^n$. From this, we conclude that

$$\begin{aligned} \lim _{t\rightarrow \infty }z(x,t)=u_\infty (x) \quad \text{ uniformly } \text{ on } \; \mathbb{R }^n \end{aligned}$$

(28)

for some function $u_\infty \in \mathrm{Lip}(\mathbb{T }^n)$.

Fix any $\delta >0$. By (28) there is a constant $\tau >0$ such that

$$\begin{aligned} \Vert z(\cdot ,\tau )-u_\infty \Vert _{L^\infty (\mathbb{R }^n)}<\delta , \end{aligned}$$

Then, by (26) there is a $j\in \mathbb{N }$ such that

$$\begin{aligned} \Vert z(\cdot ,\tau )-u(\cdot ,\tau +\tau _j)\Vert _\infty <\delta . \end{aligned}$$

Hence,

$$\begin{aligned} \Vert u(\cdot ,\tau +\tau _j)-u_\infty \Vert _\infty <2\delta . \end{aligned}$$

By the contraction property (Theorem 2), we see that for any $t\ge \tau +\tau _j$,

$$\begin{aligned} \Vert u(\cdot ,t)-u_\infty \Vert _\infty \le \Vert u(\cdot ,\tau +\tau _j)-u_\infty \Vert _\infty <2\delta , \end{aligned}$$

which completes the proof.

2.2 Under assumption (A6)$_{\scriptscriptstyle -}$

In addition to (A1)–(A5), we assume throughout this subsection that (A6)$_{\scriptscriptstyle -}$ holds.

To accommodate the previous $w$ to (A6)$_{\scriptscriptstyle -}$, we modify and replace it by the new function, which we denote by the same symbol, given by

$$\begin{aligned} w(x,t)=\max _{0\le s\le t}(u(x,t)-v_0(x)-\theta (u(x,s)-v_0(x)-\eta (s-t)), \end{aligned}$$

where $(\eta ,\theta )$ is chosen arbitrarily in $(0,\,\eta _0)\times (1,\,\theta _0)$ and the constants $\eta _0$ and $\theta _0$ are those from (A6)$_{\scriptscriptstyle -}$.

Lemma 9

We have

$$\begin{aligned} -C_0(\theta -1)\le w(x,t)\le C_0 \quad \text{ for } \text{ all } \; (x,t)\in \,\overline{\!Q}. \end{aligned}$$

Proof

Recall that $0\le u(x,t)-v_0(x)\le C_0$ for all $(x,t)\in \,\overline{\!Q}$, and note that for all $(x,t)\in \,\overline{\!Q}$,

$$\begin{aligned} w(x,t)\ge u(x,t)-v_0(x)-\theta (u(x,t)-v_0(x))&= (1-\theta )(u(x,t)-v_0(x))\\&\ge -C_0(\theta -1) \end{aligned}$$

and

$$\begin{aligned} w(x,t)\le \max _{ 0\le s\le t} (u(x,t)-v_0(x))\le C_0. \end{aligned}$$

$\square$

We have the following proposition similar to Proposition 6.

Proposition 10

The function $w$ is a subsolution of

$$\begin{aligned} \min \{w(x,t),w_t(x,t)\!-\!\omega _{H,R}(|D_x w(x,t)|)\!+\!\psi \}\le 0 \!\quad \! \text{ in } \; (x,t)\!\in \!\mathbb{R }^n\times (T,\,\infty ), \end{aligned}$$

(29)

where $\psi =\psi (\theta ,\eta )>0$ is the constant from (A6)$_{\scriptscriptstyle -}$, $T:=C_0/\eta$ and $R:=(2\theta _0+1)L$.

Since the proof of the above proposition is very similar to that of Proposition 6, we present just an outline of it.

Outline of proof

Note that for any $(x,t)\in \mathbb{R }^n\times (T,\,\infty )$ and $s\in [0,\,t-T)$,

$$\begin{aligned} u(x,t)\!-\!v_0(x)\!-\!\theta (u(x,s)\!-\!v_0(x)\!-\!\eta (s\!-\!t))&\le C_0\!-\!\theta \eta (t\!-\!s)\nonumber \\&< C_0\!-\theta \eta T\!=\!-(\theta \!-\!1)C_0. \end{aligned}$$

(30)

Hence, in view of Lemma 9, for any $(x,t)\in \mathbb{R }^n\times (T,\,\infty )$ we have

$$\begin{aligned} w(x,t)&= \max _{t-T\le s\le t}[u(x,t)-v_0(x)-\theta (u(x,s)-v_0(x)-\eta (s-t))]\\&= \max _{-T\le s\le 0}[u(x,t)-v_0(x)-\theta (u(x,s+t)-v_0(x)-\eta s)]. \end{aligned}$$

From this latter expression of $w$, as the functions $u$ and $v_0$ are Lipschitz continuous in $\,\overline{\!Q}$ and $\mathbb{R }^n$, respectively, we see that $w$ is Lipschitz continuous in $\mathbb{R }^n\times [T,\,\infty )$. Also, from (30) we see that for any $(x,t)\in \mathbb{R }^n\times (T,\,\infty )$, if

$$\begin{aligned} w(x,t)=u(x,t)-v_0(x)-\theta (u(x,s)-v_0(x)-\eta (s-t)) \end{aligned}$$

for some $0\le s\le t$, then $s\ge t-T>0$.

To see that (29) holds, we fix any test function $\phi _0\in C^1(\mathbb{R }^n\times (T,\,\infty ))$ and assume that $w-\phi _0$ attains a strict maximum at a point $(\hat{x},\hat{t})$.

Following the same arguments as in the proof under (A6)$_{\scriptscriptstyle +}$, we are led to the inclusions

$$\begin{aligned} \left\{ \begin{array}{l} \hat{p}\in \,\overline{\!D}{}^+v_0(\hat{x}),\\ \left( \hat{q}, \eta \right) \in \,\overline{\!D}{}^-u(\hat{x},\hat{s}),\\ \left( D_x\phi _0(\hat{x},\hat{t})+\theta \hat{q}-(\theta -1)\hat{p}, \phi _{0,t}(\hat{x},\hat{t})+\theta \eta \right) \in \,\overline{\!D}{}^+u(\hat{x},\hat{t}) \end{array} \right. \end{aligned}$$

(31)

for some $\hat{p},\hat{q}\in \mathbb{R }^n$.

Using (31), we observe that $H(\hat{x},\hat{p})\le 0$ and $\eta +H(\hat{x},\hat{q})\ge 0$. Hence, by condition (A6)$_{\scriptscriptstyle -}$, we get

$$\begin{aligned} H(\hat{x},\hat{p}+\theta (\hat{q}-\hat{p}))\ge -\theta \eta +\psi . \end{aligned}$$

Moreover, we compute that

$$\begin{aligned} 0&\ge \phi _{t}(\hat{x},\hat{t},\hat{s})+\theta \eta +H(\hat{x},D_x\phi (\hat{x},\hat{t},\hat{s})+\theta \hat{q}-(\theta -1)\hat{p})\\&\ge \phi _{0,t}(\hat{x},\hat{t})+\theta \eta -\omega _{H,R}(|D_x\phi _0(\hat{x},\hat{t})|) +H(\hat{x},\theta \hat{q}-(\theta -1)\hat{p})\\&\ge \phi _{0,t}(\hat{x},\hat{t}) -\omega _{H,R}(|D_x\phi _0(\hat{x},\hat{t})|) +\psi . \end{aligned}$$

Note that, as above, $|\hat{p}+\theta (\hat{q}-\hat{p})|\le R$ and $|D_x\phi _0(\hat{x},\hat{t})+\theta \hat{q}-(\theta -1)\hat{p}|\le L.$ This completes the proof. $\square$

Outline of proof of Theorem 4 under (A6)$_{\scriptscriptstyle -}$ Using Proposition 10 and arguing as the proof of Lemma 8, we deduce that

$$\begin{aligned} \lim _{t\rightarrow \infty }\max \{w(x,t),0\}=0 \quad \text{ uniformly } \text{ in } \; \mathbb{R }^n. \end{aligned}$$

We fix any $\varepsilon >0$ and choose a constant $T_\varepsilon \equiv T_{\varepsilon ,\eta ,\theta }>T$ so that for any $t\ge T_\varepsilon$,

$$\begin{aligned} w(x,t)\le \varepsilon \quad \text{ for } \text{ all } \; x\in \mathbb{R }^n. \end{aligned}$$

Let $t\ge T_\varepsilon$ and $x\in \mathbb{R }^n$. For any $0\le s\le t$, we have

$$\begin{aligned} u(x,t)-v_0(x)\le \varepsilon +u(x,s)-v_0(x)+(\theta -1)C_0+\theta \eta (t-s). \end{aligned}$$

We may assume that $T_\varepsilon >1$, and from the above, for any $0\le s\le 1$, we have

$$\begin{aligned} u(x,t)\le u(x,t-s)+(\theta -1)C_0+\theta \eta +\varepsilon . \end{aligned}$$

(32)

Since $u\in \mathrm{Lip}(\mathbb{T }^n\times (0, \infty ))$ and it is bounded in $\,\overline{\!Q}$, the Ascoli–Arzela theorem assures that there is a sequence $\{\tau _j\}_{j\in \mathbb{N }}\subset (0,\infty )$ diverging to infinity such that for some function $z\in \mathrm{Lip}(\mathbb{T }^n\times \mathbb{R })$,

$$\begin{aligned} \lim u(x,t+\tau _j)=z(x,t) \quad \text{ locally } \text{ uniformly } \text{ in } \; \mathbb{R }^{n+1}. \end{aligned}$$

We see immediately from (32) that the function $z(x,t)$ is nonincreasing in $t$ for every $x$. Furthermore, we infer that for some function $u_\infty \in C(\mathbb{T }^n)$,

$$\begin{aligned} \lim _{t\rightarrow \infty }z(x,t)=u_\infty (x) \quad \text{ uniformly } \text{ in }\; \mathbb{R }^n. \end{aligned}$$

As exactly under (A6)$_{\scriptscriptstyle +}$, we deduce from this that

$$\begin{aligned} \lim _{t\rightarrow \infty } u(x,t)=u_\infty (x) \quad \text{ uniformly } \text{ in } \; \mathbb{R }^n, \end{aligned}$$

which completes the proof.

3 Conditions (A6)$_{\scriptscriptstyle \pm }$

First of all we restate the conditions (A6)$_{\scriptscriptstyle \pm }$ in [3] as (A)$_{\scriptscriptstyle \pm }$:

(A)$_{\scriptscriptstyle +}$ There exists $\eta _{0}>0$ such that, for any $\eta \in (0,\eta _{0})$, there exists $\nu =\nu (\eta )>0$ such that for all $x,p,q\in \mathbb{R }^n$ and $\theta >1$, if $H(x,q)\ge \eta$ and $H(x,p)\le 0$, then

$$\begin{aligned} H(x,p+\theta (q-p))\ge \theta H(x,q)+\nu (\theta -1). \end{aligned}$$

(A)$_{\scriptscriptstyle -}$ There exists $\eta _{0}>0$ such that, for any $\eta \in (0,\eta _{0})$, there exists $\nu =\nu (\eta )>0$ such that for all $x,p,q\in \mathbb{R }^{n}$ and $\lambda \in [0,\,1]$, if $H(x,q)\le -\eta$ and $H(x,p)\le 0$, then

$$\begin{aligned} H(x,(1-\lambda )p+\lambda q)\le \lambda H(x,q)-\nu \lambda (1-\lambda ). \end{aligned}$$

Conditions (A6)$_{\scriptscriptstyle \pm }$ and (A)$_{\scriptscriptstyle \pm }$ can be considered as a sort of strict convexity requirements on the function $H(x,p)$ in $p$ near the points where $H$ vanishes ((A6)$_{\scriptscriptstyle +}$ and (A)$_{\scriptscriptstyle +}$ are the ones for those points $(x,p)$ where $H(x,p)\ge 0$, while (A6)$_{\scriptscriptstyle -}$ and (A)$_{\scriptscriptstyle -}$ are for those points where $H\le 0$).

The condition (H4) in [5] has a general feature more than (A)$_{\scriptscriptstyle +}$ above, and its additional generality is in the point that includes the key assumption in Namah–Roquejoffre [19]. If we push this point aside, then the condition (H4) in [5] is same as (A)$_{\scriptscriptstyle +}$ above.

Now, we give comparison between (A6)$_{\scriptscriptstyle +}$ and (A)$_{\scriptscriptstyle +}$. Let $\eta _0$, $\theta _0$ and $\psi (\eta ,\theta )$ be the positive constants from (A6)$_{\scriptscriptstyle +}$. Note that the key inequality in (A6)$_{\scriptscriptstyle +}$ holds with $\psi (\eta ,\theta )$ replaced by $\min \{\psi (\eta ,\theta ),\, 1\}$. Thus, the behavior of the function $H$ where the value of $H$ is large (larger than $\eta _0\theta _0 +1$), is irrelevant to condition (A6)$_{\scriptscriptstyle +}$, while (A)$_{\scriptscriptstyle +}$ requires a certain growth of the function $H$ where its value is positive. The function $H$ on $\mathbb{R }^n$ (see Fig. 1) given by

$$\begin{aligned} H(p)=\max \{\min \{|p|^2, 1\}, |p|^2/4\} \end{aligned}$$

satisfies (A2)–(A5) and (A6)$_{\scriptscriptstyle +}$, as is easily checked. However, if $p=0$, $|q|=1$ and $1<\theta <2$, then we have

$$\begin{aligned} H(p+\theta (q-p))=H(\theta q)=1<\theta =\theta H(q). \end{aligned}$$

Therefore, (A)$_{\scriptscriptstyle +}$ does not hold with this Hamiltonian $H(x,p)=H(p)$.

Fig. 1

Hamiltonian satisfying $(\text{ A }6)_{+}$ and not $(\text{ A })_{+}$

The difference of two conditions observed above is concerned with the behavior of the Hamiltonian $H(x,p)$ where $H$ is large.

The following example shows that (A)$_{\scriptscriptstyle +}$ is a stronger requirement on $H$ than (A6)$_{\scriptscriptstyle +}$ even in a neighborhood of the points $(x,p)$ where $H$ vanishes. In this regard, the difference between two conditions is that the term $\psi (\eta ,\theta )$ in (A6)$_{\scriptscriptstyle +}$ depends generally on $\eta ,\,\theta$ while the term $\nu (\eta )(\theta -1)$ in (A)$_{\scriptscriptstyle +}$ depends linearly in $\theta -1$.

We define the function $H_0$ (see Fig. 2) and $H$ in $C(\mathbb{R })$ by

$$\begin{aligned} H_0(p)= \left\{ \begin{array}{ll} 0 &{} \text{ for } \; p\le 0,\\ p+(p-1)^2 &{} \text{ if } \; p\ge 1, \\ p/2+2(p-1/2)^2 &{} \text{ if } \; 1/2\le p\le 1, \\ \qquad \vdots &{} \qquad \vdots \\ p/2^{j+1}+2^{j+1}\left( p-1/2^{j+1}\right) ^2&{} \text{ if } \; 1/2^{j+1}\le p\le 1/2^j, \\ \qquad \vdots &{} \qquad \vdots \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} H(p)=|p+1|-1+H_0(p)+H_0(-p-1) \end{aligned}$$

Fig. 2

Function $H_{0}$

This Hamiltonian $H$ satisfies (A2)–(A4), and the problem

$$\begin{aligned} H(u^{\prime }(x))=0 \quad \text{ in } \; \mathbb{R }\quad \text{ and }\quad u\in C(\mathbb{T }), \end{aligned}$$

where $u^{\prime }= \mathrm{d} u/ \mathrm{d} x$, has a solution $u(x)\equiv 0$. Thus, (A5) is satisfied with our function $H$. Moreover, it is easily seen that $H$ satisfies (A6)$_{\scriptscriptstyle +}$. However, $H$ does not satisfy condition (A)$_{\scriptscriptstyle +}$. To check this, fix any $j\in \mathbb{N }$ and choose $p=0$ and $q=1/2^{j+1}$. Note that

$$\begin{aligned} H(q)=\frac{1}{2^{j+1}}+\frac{1}{2^{2j+2}}, \end{aligned}$$

and that for any $\theta \in (1,\,2)$, we have $1/2^{j+1}<\theta q<1/2^j$ and

$$\begin{aligned} H(\theta q)=\frac{\theta }{2^{j+1}}+\frac{\theta }{2^{2j+2}} +2^{j+1}\left( \frac{\theta }{2^{j+1}}-\frac{1}{2^{j+1}}\right) ^2 =\theta H(q)+\frac{(\theta -1)^2}{2^{j+1}}. \end{aligned}$$

Hence,

$$\begin{aligned} H(\theta q)-\theta H(q)=o(\theta -1) \quad \text{ as } \; \theta \rightarrow 1+, \end{aligned}$$

which violates the inequality in (A)$_{\scriptscriptstyle +}$. Note finally that $q=1/2^{j+1}$ can be taken as close to $p=0$ as we wish.

Next, we show that if $H\in C(\mathbb{T }^n\times \mathbb{R }^n)$ satisfies (A)$_{\scriptscriptstyle -}$, then it satisfies (A6)$_{\scriptscriptstyle -}$.

For this, let $H\in C(\mathbb{T }^n\times \mathbb{R }^n)$ satisfy (A6)$_{\scriptscriptstyle -}$. Let $\eta _0>0$ be the constant and $\nu$ the function on $(0, \eta _0)$ given by (A)$_{\scriptscriptstyle -}$.

Fix any $\eta \in (0, \eta _0)$ and $\theta >1$, and set $\lambda =\theta ^{-1}\in (0,\,1)$. Let $x,p,q\in \mathbb{R }^n$ and assume that $H(x,p)\le 0$ and $H(x,q)\ge -\eta$. Set

$$\begin{aligned} \psi =\psi (\eta ,\theta ):=(\theta -1)\min \{\theta ^{-1}\nu (\eta ), \eta \} =\min \{(1-\lambda )\nu (\eta ),\,(\theta -1)\eta \}. \end{aligned}$$

(33)

It is enough to show that

$$\begin{aligned} H(x,p+\theta (q-p))\ge -\theta \eta +\psi . \end{aligned}$$

(34)

To the contrary, we suppose that

$$\begin{aligned} H(x,p+\theta (q-p))< -\theta \eta +\psi . \end{aligned}$$

(35)

Set $r=p+\theta (q-p)$ and note that $q=\lambda r+(1-\lambda ) p$. Note by the choice of $\psi$ that

$$\begin{aligned} H(x,r)< -\theta \eta +(\theta -1)\eta =-\eta . \end{aligned}$$

Hence, using (A)$_{\scriptscriptstyle -}$, (34) and (33), we deduce that

$$\begin{aligned} H(x,q)\!=\!H(x,\lambda r\!+\!(1\!-\!\lambda )p)\!\le \! \lambda H(x,r)\!-\!\nu (\eta )\lambda (1\!-\!\lambda ) \!<\!\lambda (\!-\,\theta \!+\!\psi )\!-\!\psi \lambda \!=\!-\eta . \end{aligned}$$

This is a contradiction, which shows that (34) holds.

Now, let $H\in C(\mathbb{T }^n\times \mathbb{R }^n)$ satisfy (A6)$_{\scriptscriptstyle +}$, and we show that for each $x\in \mathbb{R }^n$ the sublevel set $\{p\in \mathbb{R }^n : H(x,p)\le 0\}$ is convex.

To do this, we fix any $x\in \mathbb{R }^n$ and let $p_1,p_2\in K:=\{p\in \mathbb{R }^n : H(x,p)\le 0\}$. We need to show that

$$\begin{aligned} \lambda p_1+(1-\lambda )p_2\in K \quad \text{ for } \text{ all }\; \lambda \in [0, 1]. \end{aligned}$$

(36)

We suppose that this is not the case and will get a contradiction.

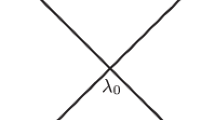
Let $\eta _0>0$ and $\theta _0>0$ be the constants from (A6)$_{\scriptscriptstyle +}$. Then, setting

$$\begin{aligned} \lambda _0=\sup \{\lambda \in [0, 1]: \lambda p_1+(1-\lambda )p_2\not \in K\}, \end{aligned}$$

we have

$$\begin{aligned} \lambda _0 p_1+(1-\lambda _0)p_2\in K \quad \text{ by } \text{ the } \text{ continuity } \text{ of }\; H. \end{aligned}$$

By the definition of $\lambda _0$, we may select a $\lambda \in (0, \lambda _0)$ so that

$$\begin{aligned} \lambda p_1+(1-\lambda )p_2\not \in K \quad \text{ and } \quad \lambda \theta _0>\lambda _0. \end{aligned}$$

Set

$$\begin{aligned} q&:\,\,=&\lambda p_1+(1-\lambda )p_2=p_2+\lambda (p_1-p_2),\\ \theta&:\,\,=&\lambda _0/\lambda \in (1, \theta _0), \end{aligned}$$

and note that $H(x,q)>0$. Fix an $0<\eta <\eta _0$ so that $H(x,q)\ge \eta$, and use condition (A6)$_{\scriptscriptstyle +}$, to get

$$\begin{aligned} H(x,p_2+\theta (q-p_2))>\theta \eta >0, \end{aligned}$$

and moreover,

$$\begin{aligned} 0<H(x,p_2+\theta (q-p_2))=H(x,\lambda _0p_1+(1-\lambda _0)p_2)\le 0. \end{aligned}$$

This is a contradiction.

An argument similar to the above guarantees that if $H\in C(\mathbb{T }^n\times \mathbb{R }^n)$ satisfies (A6)$_{\scriptscriptstyle -}$, then the sublevel set $\{p\in \mathbb{R }^n : H(x,p)<0\}$ is convex for every $x\in \mathbb{R }^n$. We leave it for the interested reader to check this convexity property.

The following example of $H(x,p)=H(p)$ explicitly shows that condition (A)$_{\scriptscriptstyle -}$ is more stringent than (A6)$_{\scriptscriptstyle -}$. Define the functions $f, g\in C(\mathbb{R })$ by

$$\begin{aligned}&\displaystyle f(p)= {\left\{ \begin{array}{ll} 0&{}\text{ if } \; p\le 0 \; \text{ or } \; p\ge 1, \\ -p/2&{}\text{ if } \; 0\le p\le 1/2,\\ -(p-1)^2&{}\text{ if } \; 1/2\le p\le 1, \end{array}\right. }\\&\displaystyle g(p)=-p+\sum _{k=1}^\infty 2^{-k}f(2^k p), \end{aligned}$$

and then $H\in C(\mathbb{R })$ (see Fig. 3) by

$$\begin{aligned} H(p)=\max \{g(p), g(1-p)\}. \end{aligned}$$

Fig. 3

Hamiltonian satisfying $(\text{ A }6)_{-}$ and not $(\text{ A })_{-}$

We do not give the detail, but observing that in the $py$ plane, for each slope $m<0$, the half line $y=mp$, $p>0$, meets the graph $y=H(p)$ at exactly one point, we can deduce that the function $H$ satisfies (A6)$_{\scriptscriptstyle -}$. On the other hand, setting $p=0$ and $q=1/2^k$, with $k\in \mathbb{N }$, observing that if $\frac{1}{2}\le \lambda \le 1$, then $1/2^{k+1}\le \lambda q\le 1/2^k$ and that for any $\frac{1}{2}\le \lambda \le 1$,

$$\begin{aligned} H(\lambda q)=-\frac{k+1}{2^{k+1}} -\frac{(\lambda -1)^2}{2^k}, \end{aligned}$$

and hence,

$$\begin{aligned} H(q)&= -\frac{k+1}{2^{k+1}}, \\ H(\lambda q)&= \lambda H(q)-\frac{(\lambda -1)^2}{2^{k}}, \end{aligned}$$

we may deduce that (A)$_{\scriptscriptstyle -}$ does not hold with the current function $H$.

Next, we remark that under hypotheses (A2)–(A4), conditions (A6)$_{\scriptscriptstyle +}$ and (A6)$_{\scriptscriptstyle -}$ are equivalent to the following (A7)$_{\scriptscriptstyle +}$ and (A7)$_{\scriptscriptstyle -}$, respectively.

(A7)$_{\scriptscriptstyle +}$ There exist constants $\eta _0>0$ and $\theta _0>1$ such that for all $(\eta ,\theta )\in (0,\eta _0)\times (1,\theta _0)$, $x, p,q\in \mathbb{R }^n$, if $H(x,p)\le 0$ and $H(x,q)\ge \eta$, then

$$\begin{aligned} H(x,p+\theta (q-p))> \eta \theta . \end{aligned}$$

(A7)$_{\scriptscriptstyle -}$ There exist constants $\eta _0>0$ and $\theta _0>1$ and for all $(\eta ,\theta )\in (0,\eta _0)\times (1,\theta _0)$, $x, p,q\in \mathbb{R }^n$, if $H(x,p)\le 0$ and $H(x,q)\ge -\eta$, then

$$\begin{aligned} H(x,p+\theta (q-p))>-\eta \theta . \end{aligned}$$

Indeed, it is clear that (A6)$_{\scriptscriptstyle \pm }$ imply (A7)$_{\scriptscriptstyle \pm }$, respectively. On the other hand, assuming that (A7)$_{\scriptscriptstyle +}$ holds, choosing $R>0$ so large that

$$\begin{aligned} H(x,p)>\eta _0\theta _0 \quad \text{ if } \; |p|>R, \end{aligned}$$

where $\eta _0>0$ and $\theta _0>1$ are the constants from (A7)$_{\scriptscriptstyle +}$, and setting

$$\begin{aligned} \psi (\eta ,\theta ) =\min \{H(x,p+\theta (q-p))-\theta \eta \,:\,x\in \mathbb{T }^n, H(x,p)\le 0, H(x,q)\ge \eta \} \end{aligned}$$

for any $(\eta ,\theta )\in (0,\,\eta _0)(1, \theta _0)$ we observe that $\psi (\eta ,\theta )$ is positive and satisfies

$$\begin{aligned} H(x,p+\theta (q-p))\ge \eta \theta +\psi (\eta ,\theta ) \end{aligned}$$

for all $(x,p,q)\in \mathbb{R }^{3n}$ such that $H(x,p)\le 0$ and $H(x,q)\ge \eta$, which shows that (A6)$_{\scriptscriptstyle +}$ holds. Similarly, we see that (A7)$_{\scriptscriptstyle -}$ implies (A6)$_{\scriptscriptstyle -}$.

Finally, we remark that under (A2)–(A4), conditions (A6)$_{\scriptscriptstyle +}$ and (A6)$_{\scriptscriptstyle -}$ are equivalent to the following (A8)$_{\scriptscriptstyle +}$ and (A8)$_{\scriptscriptstyle -}$, respectively.

(A8)$_{\scriptscriptstyle +}$ There exist constants $\eta _0>0$ and $\theta _0>1$ and for each $(\eta ,\theta )\in (0,\eta _0)\times (1,\theta _0)$ a constant $\psi =\psi (\eta ,\theta )>0$ such that for all $x, p,q\in \mathbb{R }^n$, if $H(x,p)=0$ and $H(x,q)=\eta$, then

$$\begin{aligned} H(x,p+\theta (q-p))\ge \eta \theta +\psi . \end{aligned}$$

(A8)$_{\scriptscriptstyle -}$ There exist constants $\eta _0>0$ and $\theta _0>1$ and for each $(\eta ,\theta )\in (0,\eta _0)\times (1,\theta _0)$ a constant $\psi =\psi (\eta ,\theta )>0$ such that for all $x, p,q\in \mathbb{R }^n$, if $H(x,p)=0$ and $H(x,q)=-\eta$, then

$$\begin{aligned} H(x,p+\theta (q-p))\ge -\eta \theta +\psi . \end{aligned}$$

It is clear that (A6)$_{\scriptscriptstyle \pm }$ imply (A8)$_{\scriptscriptstyle +}$, respectively.

We next show that (A8)$_{\scriptscriptstyle +}$ implies (A7)$_{\scriptscriptstyle +}$, which is equivalent to (A6)$_{\scriptscriptstyle +}$. We leave it to the reader to check that (A8)$_{\scriptscriptstyle -}$ implies (A7)$_{\scriptscriptstyle -}$.

Let $\eta _0$ and $\theta _0$ be the constants from (A8)$_{\scriptscriptstyle +}$. We may assume, by replacing $\theta _0$ by a smaller one if needed, that $\theta _0<2$.

Fix any $0<\eta <\eta _0/2$ and $(x,p,q)\in \mathbb{R }^{3n}$ such that $H(x,p)\le 0$ and $H(x,q)\ge \eta$. It is enough to show that for all $1<\theta <\theta _0$,

$$\begin{aligned} H(x,p+\theta (q-p)>\theta \eta . \end{aligned}$$

(37)

We assume for contradiction that (37) does not hold. We set

$$\begin{aligned} \Theta =\{\theta \in (1,\theta _0)\,:\,H(x,p+\theta (q-p))\le \theta \eta \}. \end{aligned}$$

Note by the above assumption that $\Theta \ne \emptyset$ and set $\hat{\theta }:=\inf \Theta$. It is clear that $1\le \hat{\theta }<\theta _0$, $H(x,p+\hat{\theta }(q-p))=\hat{\theta }\eta$ since $H(x,q)\ge \eta$ and $H(x,p+\theta (q-p))>\theta \eta$ if $1<\theta <\hat{\theta }$.

In what follows, we write $H(r):=H(x,r)$ and $q_\theta =p+\theta (q-p)$ for $0\le \theta <\theta _0$. We fix a $\lambda \in [0,\,1)$ so that $H(p+\lambda (q-p))=0$. Note that $H(q_\lambda )=0$.

Consider the case where $\hat{\theta }=1$. In this case we have $q_{\hat{\theta }}=q$ and $H(q)=\eta$. By (A8)$_{\scriptscriptstyle +}$, we get

$$\begin{aligned} H(q_{\lambda }+\rho (q-q_{\lambda }))>\rho \eta \quad \text{ for } \text{ all } \; \rho \in (1,\theta _0). \end{aligned}$$

(38)

Noting that

$$\begin{aligned} q_\lambda +\rho (q-q_\lambda )&= p+\lambda (q-p)+\rho (q-p-\lambda (q-p))\\&= p+(\lambda +(1-\lambda )\rho )(q-p), \end{aligned}$$

from (38) we get

$$\begin{aligned} H(p+(\lambda +(1-\lambda )\rho )(q-p))>\rho \eta \ge (\lambda +(1-\lambda )\rho )\eta \quad \text{ for } \text{ all } \; \rho \in (1,\theta _0), \end{aligned}$$

which implies that $\Theta \cap (1,\,\lambda +(1-\lambda )\theta _0)=\emptyset$. This ensures that $\hat{\theta }\ge \lambda +(1-\lambda )\theta _0>1$, which contradicts that $\hat{\theta }=1$.

Consider next the case where $\hat{\theta }>1$ (see Fig. 4). Recall that $H(q_{\hat{\theta }})=\hat{\theta }\eta <2\eta <\eta _0$ and $H(q_\theta )>\theta \eta$ for all $\theta \in (1, \hat{\theta })$. Setting $\eta _\theta :=H(q_\theta )$, we observe that if $1<\theta <\hat{\theta }$ is close to $\hat{\theta }$, then $\theta \eta <\eta _\theta <\eta _0$. For any such $\theta$, by (A8)$_{\scriptscriptstyle +}$, we get

$$\begin{aligned} H(q_\lambda +\rho (q_\theta -q_\lambda ))>\rho \eta _\theta \quad \text{ for } \text{ all } \; \rho \in (1,\theta _0). \end{aligned}$$

(39)

Note that $q_\lambda +\rho (q_\theta -q_\lambda ) =p+(\lambda +\rho (\theta -\lambda ))(q-p)$. We select $\hat{\rho }$ so that $\hat{\theta }=\lambda +\hat{\rho }(\theta -\lambda )$ or, equivalently, $\hat{\rho }=(\hat{\theta }-\lambda )/(\theta -\lambda )$. Since $\theta$ is assumed to be close enough to $\hat{\theta }$, we may assume that $\hat{\rho }\in (1,\,\theta _0)$. Thanks to (39), we get

$$\begin{aligned} \hat{\theta }\eta =H(q_{\hat{\theta }}) = H(q_\lambda +\hat{\rho }(q_\theta -q_\lambda ))>\hat{\rho }\eta _\theta >\frac{\hat{\theta }-\lambda }{\theta -\lambda }\eta \theta . \end{aligned}$$

Thus, we get $\hat{\theta }(\theta -\lambda )>\theta (\hat{\theta }-\lambda )$ or, equivalently, $\lambda (\hat{\theta }-\theta )<0$. This is a contradiction. We thus see that (A8)$_{\scriptscriptstyle +}$ implies (A7)$_{\scriptscriptstyle +}$.

Fig. 4

Position of $p$, $q$, $q_{\lambda }$, etc

4 A generalization of (A6)$_{\scriptscriptstyle \pm }$

We recall that the following conditions on the Hamiltonian $H\in C(\mathbb{T }^n\times \mathbb{R }^n)$ has been introduced by Namah–Roquejoffre [19] in their study of the large time asymptotic behavior of solutions of (CP).

• (NR1) The function $H(x,p)$ is convex in $p\in \mathbb{R }^n$ for every $x\in \mathbb{R }^n$.

• (NR2) $\min _{p\in \mathbb{R }^n}H(x,p)=H(x,0)$ for all $x\in \mathbb{R }^n$.

• (NR3) $\max _{x\in \mathbb{R }^n}H(x,0)=0$.

• (NR4) $\lim _{r\rightarrow \infty }\inf \{H(x,p): (x,p)\in \mathbb{T }^n\times \mathbb{R }^n,\, |p|\ge r\}=\infty$.

Assume for the moment that $H\in C(\mathbb{T }^n\times \mathbb{R }^n)$ satisfies (NR3). Then the function $v(x)\equiv 0$ solves in the classical sense

$$\begin{aligned} H(x,Dv(x))=H(x,0) \quad \text{ in }\; \mathbb{R }^n. \end{aligned}$$

Here, if $H(x,0)<0$ for some points $x$, then $v$ is a “strict” subsolution of $H(x,Du)=0$ in the set $\{x\in \mathbb{R }^n\,:\,H(x,0)<0\}$.

We take this observation into account and modify conditions (A6)$_{\scriptscriptstyle \pm }$ as follows. The new conditions depend on our choice of a subsolution $v_0$ of (1), which plays the same role as the function $v_0$ in the proof of Theorem 4. As we have already noted in Remark 1, the function $v_0$ in the proof of Theorem 4 is needed to be just a subsolution of (1) and the outcome may depend on our choice of $v_0$. Now we fix a subsolution $v_0\in C(\mathbb{T }^n)$ of (1) and choose a nonnegative function $f\in C(\mathbb{T }^n)$ so that $v_0$ is a subsolution of

$$\begin{aligned} H(x,Dv_0(x))\le -f(x) \quad \text{ in } \; \mathbb{R }^n. \end{aligned}$$

(A9)$_{\scriptscriptstyle +}$ There exist constants $\eta _0>0$ and $\theta _0>1$ and for each $(\eta ,\theta )\in (0,\eta _0)\times (1,\theta _0)$ a constant $\psi =\psi (\eta ,\theta )>0$ such that for all $x, p,q\in \mathbb{R }^n$, if $H(x,p)\le -f(x)$ and $H(x,q)\ge \eta$, then

$$\begin{aligned} H(x,p+\theta (q-p))\ge \eta \theta +\psi . \end{aligned}$$

(A9)$_{\scriptscriptstyle -}$ There exist constants $\eta _0>0$ and $\theta _0>1$ and for each $(\eta ,\theta )\in (0,\eta _0)\times (1,\theta _0)$ a constant $\psi =\psi (\eta ,\theta )>0$ such that for all $x, p,q\in \mathbb{R }^n$, if $H(x,p)\le -f(x)$ and $H(x,q)\ge -\eta$, then

$$\begin{aligned} H(x,p+\theta (q-p))\ge -\eta \theta +\psi . \end{aligned}$$

The same proof as that of Theorem 4 yields the following proposition. We do not repeat its proof here, and leave it to the reader to check the detail.

Theorem 11

The assertion of Theorem 4, with (A9)$_{\scriptscriptstyle \pm }$ in place of (A6)$_{\scriptscriptstyle \pm }$, holds.

In the following, we show that if $H\in C(\mathbb{T }^n\times \mathbb{R }^n)$ satisfies (NR1)–(NR3), then (A9)$_{\scriptscriptstyle -}$ holds.

We choose $v_0$ to be the function $v_0(x)\equiv 0$. This function $v_0$ satisfies

$$\begin{aligned} H(x,Dv_0(x))=H(x,0)=-f(x) \quad \text{ for } \text{ all } \; x\in \mathbb{R }^n, \end{aligned}$$

where $f(x):=-H(x,0)$.

Fix any $x,p,q\in \mathbb{R }^{3n}, \eta >0$ such that $H(x,p)\le -f(x)$ and $H(x,q)\ge -\eta$. To prove that (A9)$_{\scriptscriptstyle -}$ holds with $f(x)=-H(x,0)$, it is enough to show that there is a constant $\psi (\eta ,\theta )>0$ such that

$$\begin{aligned} H(x,p+\theta (q-p))\ge -\theta \eta +\psi (\eta ,\theta ). \end{aligned}$$

Since

$$\begin{aligned} H(x,p)\le -f(x)=H(x,0)=\min _{r\in \mathbb{R }^n}H(x,r), \end{aligned}$$

we have $H(x,p)=-f(x)=H(x,0)$. Fix any $\theta >1$. By the convexity of $H$, we have

$$\begin{aligned} H(x,p+\theta (q-p))&\ge H(x,p)+\theta (H(x,q)-H(x,p))\\&= -f(x)+\theta (-\eta +f(x)) =-\theta \eta +(\theta -1)f(x), \end{aligned}$$

while we have

$$\begin{aligned} H(x,p+\theta (q-p))\ge H(x,0)=-f(x)=-\theta \eta +(\theta \eta -f(x)). \end{aligned}$$

Setting

$$\begin{aligned} \psi (\eta ,\theta )=\min _{x\in \mathbb{T }^n}\max \{(\theta -1)f(x), \theta \eta -f(x)\}, \end{aligned}$$

we observe that $\psi (\eta ,\theta )>0$ and

$$\begin{aligned} H(x,p+\theta (q-p))\ge -\theta \eta +\psi (\eta ,\theta ). \end{aligned}$$

Thus, $H$ satisfies (A9)$_{\scriptscriptstyle -}$.