The Effects of the Length of the Period of Commitment on the Size of Stable International Environmental Agreements

Abstract

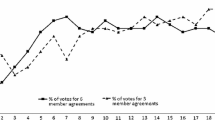
This paper extends the standard model of self-enforcing dynamic international environmental agreements by allowing the length of the period of commitment of such agreements to vary as a parameter. It analyzes the pattern of behavior of the size of stable coalitions, the stock of pollution, and the emission rate as a function of the length of the period of commitment. It is shown that the length of the period of commitment can have very significant effects on the equilibrium. At the initial date, numerical simulations reveal that as the length of commitment is increased, the potential gain from cooperation tends to diminish, increasing the incentive to ratify the agreements. This suggests that considerable attention should be given to the determination of the length of such international agreements.

Appendices

Appendix A: Proof of Condition (7)

Since, by assumption, the q _i ,i=1,…,N are time stationary over interval [kh,(k+1)h), so is $Q=\sum_{i=1}^{N} q_{i}$. Using this result along with (2) and (5), we get

where $D(Q,z_{k})=-\frac{\gamma}{2}[(\frac{Q}{\rho})^{2}f(r, h)+(z_{k}-\frac{Q}{\rho})^{2}f(r+2\rho, h)+2\frac{Q}{\rho}(z_{k}-\frac{Q}{\rho})f(r+\rho, h)]$ and where f(x,h)=(1−e ^−hx)/x for all x>0.

Appendix B: The Fully-Cooperative Equilibrium

The value function V _N (z)=NV _i (z) satisfies the Bellman equation:

$$ NV_{i}(z)= \max_{q_{i}, i \in N }\Biggl\{ \sum_{i=1}^{N} aq_{i}f(r, h)+ ND(Q,z) + Ne^{-rh}V_i\bigl(Qf( \rho, h )+ze^{- \rho h}\bigr) \Biggr\}, $$

(27)

where $Q=\sum_{i}^{N} q_{i}$. The quadratic nature of the benefit function in z suggests the guess: $V_{i}(z)=-\bar{A}z^{2}/2N-\bar{B}z/N+\bar{C}/N$. Using (11)–(13) for Ψ=V _i , n=N and for q _i ∈(0,1) we get:

$$ q_{i}(z_{k})= \frac{af(r, h)-\bar{B}Nf(\rho, h)e^{-rh} - Nz_{k}(\lambda_{2}+\bar{A}f(\rho, h)e^{-h(r+\rho)})}{N^{2}[\lambda_{1}+\bar{A}f(\rho, h)^{2}e^{-rh}]}. $$

(28)

Substituting (28) into the Bellman equation and using the envelope theorem, we obtain

$$V_{i}'(z)=-z\gamma f(r+2\rho,h)-N\lambda_{2}q_{i}(z) + e^{-h(r+\rho)}V_{i}^{'}\bigl(Nf(\rho,h)q_{i}(z)+ze^{-\rho h} \bigr),\quad \forall z\geq0. $$

Equating the coefficients of the LHS and RHS of this first-degree polynomial in z, we find that

$$\bar{A}= \Bigl[-\bar{a}_{1}+\sqrt{\bar{a}_{1}^{2}-4 \bar{a}_{2}\bar{a}_{0}} \Bigr]/2\bar{a}_{2}, $$

which is the positive root of the second degree polynomial $\bar{a}_{2}A^{2}+\bar{a}_{1}A+\bar{a}_{0}=0$, where

Given $\bar{A}$, we find:

$$\bar{B}=\frac{af(r, h)(N\lambda_{2}+\bar{A}f(\rho, h)e^{-h(r+\rho)})}{N(\lambda_{1}+\bar{A}f(\rho, h)^{2}e^{-rh})(1-e^{-h(r+\rho)})+Nf(\rho, h)e^{-rh}(N\lambda_{2}+\bar{A}f(\rho, h)e^{-h(r+\rho)})}. $$

Given $\bar{A}$ and $\bar{B}$, using (27) at the optimum, we get $\bar{C}=N\bar{\beta}[af(r, h)-\bar{B}f(\rho, h)e^{-rh}]/(1-e^{-rh})-N^{2}\bar{\beta}^{2}[N\lambda_{1}+\bar{A}f(\rho, h)^{2}e^{-rh}]/2(1-e^{-rh})$, where $\bar{\beta}=[af(r, h)-N\bar{B}f(\rho, h)e^{-rh}]/\allowbreak N^{2}[\lambda_{1}+\bar{A}f(\rho, h)^{2}e^{-rh}]$.

The dynamic evolution of the pollution stock is then

The unique solution to the equation x=φ _N (x) is

$$\bar{z}=\frac{af(r, h)-\bar{B}Ne^{-rh}f(\rho, h)}{N(\lambda_{2}+\bar{A} f(\rho, h)e^{-rh})+\rho N[\lambda_{1}+\bar{A} f(\rho, h)^{2}e^{-rh}]}. $$

Hence, ∀k=0,1,2,3,… ,

$$z_{k+1}-\bar{z}\equiv\varphi_{N}(z_{k})- \bar{z}=R_{N}(z_{k}-\bar{z}) $$

so that

$$ z_{k}=\bar{z}+(R_{N})^{k}(z_{0}- \bar{z}), \quad \forall k=0,1,2,3,\ldots , $$

(29)

where,

$$R_{N}= \frac{\lambda_{1}e^{-\rho h}-\lambda_{2}f(\rho, h)}{\lambda_{1}+\bar{A}f(\rho, h)^{2}e^{-rh}}. $$

We have 1>R _N . Indeed, because all the parameters are nonnegative and $\bar{A}>0$, we have the following inequality:

$$\bigl(1-e^{-\rho h}\bigr)\lambda_{1}+\bar{A}f(\rho, h)^{2}e^{-rh}+\lambda_{2}f(\rho, h)>0. $$

Rearranging the terms of this inequality, we get

$$\lambda_{1}+\bar{A}f(\rho, h)^{2}e^{-rh}> \lambda_{1}e^{-\rho h}-\lambda_{2}f(\rho, h). $$

Dividing the LHS and the RHS of the last inequality by its LHS, we obtain 1>R _N . The sequence $z_{k}-\bar{z}$ defined in (29) being a geometric progression, a necessary and sufficient condition for z _k to converge is 1>R _N >−1. It has been established that 1>R _N . Therefore, if and only if R _N >−1, z _k converges and its limit is $\bar{z}$. It converges monotonically if R _N >0. The steady-state emission rate exists if and only R _N >−1 and is given by

$$ \bar{q}_{i}=\frac{af(r, h)-N\bar{B}f(\rho, h)e^{-rh} - \bar{z} N[\lambda_{2}+\bar{A}f(\rho, h)e^{-h(r+\rho)}]}{N^2[\lambda_{1}+\bar{A}f(\rho, h)^{2}e^{-rh}]}. $$

Notice that we have 0<q _i (z _k )<1. Indeed, let us assume that inequalities from (17) hold. On the one hand, we must have $af(r, h)< N^{2}[\lambda_{1}+\bar{A}e^{-rh}f(\rho, h)^{2}]+ N\bar{B}f(\rho, h)e^{-rh}\allowbreak +z_{k}N[\lambda_{2}+\bar{A}f(\rho, h)e^{-h(r+\rho)}]$ which, rearranging, yields $af(r, h)-N\bar{B}f(\rho, h)e^{-rh}-z_{k}N[\lambda_{2}+\bar{A}f(\rho, h)e^{-h(r+\rho)}]<N^{2}[\lambda_{1}+\bar{A}e^{-rh}f(\rho, h)^{2}]$. Dividing the two sides of this inequality by its RHS, one gets q _i (z _k )<1. On the other hand, it is easy to show that $af(r, h)-N\bar{B}f(\rho, h)e^{-rh}\geq N[\lambda_{2}+\bar{A}f(\rho, h)e^{-h(r+\rho)}]\bar{z}$. Since from (29) we have $\bar{z}> z_{2k}\geq 0$, it then follows that $af(r, h)-N\bar{B}f(\rho, h)e^{-rh}> N[\lambda_{2}+\bar{A}f(\rho, h)e^{-h(r+\rho)}]z_{2k}$. Rearranging this inequality, we can see that the numerator of (28) is positive at the point z _2k . Since the denominator of (28) is always positive, we can conclude that q _i (z _2k )>0. Unfortunately, we have not been able to prove analytically that q _i (z _2k+1)>0, k=0,1,2,… . However, we take into account this constraint in our simulations.

Appendix C: Proof of Statements in Sect. 4

Making use of (10) and the quadratic approximation $\varPsi(z)=-\frac{A}{2}z^{2}- Bz + C$, for all z, nonsignatories will emit one at each period if and only if

$$ af(r, h)\geq \lambda_1 Q +z_{k}\lambda_2+f(\rho, h)e^{-rh}\bigl\{B+A\bigl[f( \rho, h)Q+z_{k}e^{-\rho h}\bigr]\bigr\}. $$

(30)

Notice that, Q≤N; z _k ≤N/ρ and f(ρ,h)Q+z _k e ^−ρh≤N/ρ. Replacing Q, z _k and f(ρ,h)Q+z _k e ^−ρh by their upper bound in (30) yields

$$ af(r, h)\geq N(\lambda_1+ \lambda_2 /\rho)+f(\rho, h)e^{-rh}(B+AN/\rho), $$

(31)

which is condition (19). Thus, if (19) holds, it will be optimal for a nonsignatory to play q _j =1 at each period.

Given the quadratic approximation of Ψ, for q _j =1, relations (11)–(13) can be rewritten as

(32)

(33)

(34)

Solving (34), we get q _i (n,z _k )=1 if and only if 1≤n≤n ₀(z _k )≡af(r,h)/τ(z _k ,h).

Pick $\bar{n}_{1}(z_{k})$ and $\bar{n}_{2}(z_{k})$ to be the two roots of the second degree equation in n: −n ²[λ ₁+Ae ^−rh f(ρ,h)²]+nτ(z _k ,h)=af(r,h). Their expressions are given by (21). Solving (32) yields q _i (n,z _k )=0 if and only if we have $\bar{n}_{1}(z_{k})\leq n \leq \bar{n}_{2}(z_{k})$.

Solving (33), we obtain

$$ 0\leq q_{i}(n, z_{k})= \frac{a f(r, h)+n^{2}(\lambda_1+Ae^{- r h}f( \rho, h )^{2})-n\tau(z_{k}, h)}{n^{2}(\lambda_1+Ae^{- r h}f(\rho, h )^{2})} \leq 1, $$

(35)

if and only if $n\in[\bar{n}_{0}(z_{k}), \bar{n}_{1}(z_{k})]$.

As illustrated in Fig. 5, $\bar{n}_{1}(z_{k})$ and $\bar{n}_{2}(z_{k})$ are two positive real numbers but only if there exists n∈(0,N) for which −n ²[λ ₁+Ae ^−rh f(ρ,h)²]+nτ(z _k ,h) lies above af(r,h). In addition, $\bar{n}_{1}(z_{k})< N< \bar{n}_{2}(z_{k})$ is satisfied only when we have the following:

$$ -N^{2}\bigl[\lambda_{1}+Ae^{-rh}f( \rho, h )^{2}\bigr]+N\tau(z_{k}, h)>af(r, h). $$

(36)

Fig. 5

Critical values for n

Notice that (i) τ(z,h) is increasing in z; (ii) our simulations show that for z ₀ lying below the steady state of the noncooperative equilibrium: N/ρ, the stock of pollution increases over time so that its lower bound is z ₀; (iii) z ₀<N/ρ, implies that τ(z _k ,h)≥τ(z ₀,h), k=0,1,2… ; (iv) if we replace z _k by z ₀ in (36), we will get exactly the condition in (20). Thus, if the condition −N ²[λ ₁+Ae ^−rh f(ρ,h)²]+Nτ(z ₀,h)>af(r,h) holds, it will be so for (36). The inequality (20) is then a sufficient condition to have $\bar{n}_{1}(z_{k})< N< \bar{n}_{2}(z_{k})$, k=0,1,2,… .

Since we have: nτ(z _k ,h)≥−n ²[λ ₁+Ae ^−rh f(ρ,h)²]+nτ(z _k ,h), when conditions (19)–(20) hold, we also have $\bar{n}_{0}(z_{k})\leq \bar{n}_{1}(z_{k})$, as illustrated in Fig. 5. Finally, making use of Q≤N; $z_{k}\leq \tilde{z}$ for all k, we have shown that $\bar{n}_{0}(z_{k})\geq 1$ when the condition (20) is satisfied.

Summarizing, if conditions (19)–(20) are satisfied, we must have two results. On the one hand, we must have $1\le\bar{n}_{0}(z_{k})< \bar{n}_{1}(z_{k})< N< \bar{n}_{2}(z_{k})$. On the other hand, nonsignatories must emit one at each period, while the typical signatory’s decision rule for emissions will be given by (23).

Appendix D: The Algorithm

This section presents the algorithm used to approximate the value function Ψ. It is made up of the eight following steps.

• (i) Generate values of h, using the formula, h _p =h _p−1+0.1; p=1,…,2499, with h ₀=0.1. We choose plausible parameters a,γ,r,ρ,z ₀, and N such that the conditions (16), (17), (19), and (20) always hold for all h _p ,p=0,…,2499.

• (ii) For each vector (a,γ,r,ρ,z ₀,N,h _p ) of parameters we consider as initial values for A,B, and C the values of the quadratic value function for the noncooperative equilibrium.

• (iii) We generate 251 values of the stocks z in the interval $[z_{0}, \tilde{z}]$ following the sequence: $z_{p}=z_{0}+p(\tilde{z}-z_{0})/250$; p=0,…,250, where $\tilde{z}$ represents the steady state of the pollution stock for the noncooperative equilibrium.

• (iv) For each value of z from (iii), compute $\bar{n}_{1}(z)$ and $\bar{n}_{2}(z)$ using (21), $\bar{n}_{0}(z)$ using (22), and q _i (n,z) using (23). Using (14) and (15), compute Λ(n,z)=V _i (n,z)−V _j (n−1,z), for Ψ(z)=−Az ²/2−Bz+C.

• (v) For each value of z, we calculate n ^∗(z), the highest value of n for which Λ(n,z)≥0.

• (vi) We then compute for each of the 251 values of z, n ^∗(z) and q _i (n ^∗(z),z). We estimate the relation Q(n ^∗(z),z)≈β+αz by linear regression that yields an estimation of (β,α).

• (vii) Replacing Q(n ^∗(z),z) by β+αz in (18) and equating the coefficient of power of z, we get the new estimation of A, B, and C, which are the following:

  

• (viii) We repeat this operation until convergence is obtained, i.e., variations of A,B, and C not greater than 5 % or the number of iteration not greater than 101.